한낮의 밝은 빛 속에서 수학자들은 방정식과 증명을 확인하고 엄밀성의 추구에 한 치의 빈틈도 없도록 노력한다. 하지만 만월의 밤에 그들은 꿈을 꾸고 별들 사이를 떠다니며 우주의 기적에 대해 탐구한다. 그들은 영감이 넘친다. 이러한 꿈이 없다면 예술도 수학도 삶도 설 자리를 잃는다.
– 마이클 아티야
2018년 9월, 20세기를 대표하는 위대한 수학자인 마이클 아티야 경Sir Michael Atiyah, 1929-2019이 역사상 가장 중요한 수학 문제로 꼽히는 리만 가설을 해결했다는 소식이 전 세계 언론사를 통해 주요뉴스로 전해졌다. 리만 가설은 무엇이고 아티야 경이 누구기에 이토록 큰 관심을 불러왔으며 그 주장의 실체는 어떤가에 대해 이야기해보고자 한다.
리만 가설
정수와 기하는 수학의 출발점이자 인간이 우주를 이해하는 가장 원초적인 틀이다. 젖먹이 아이가 수를 가늠하고 엄마의 위치를 인식하는 것부터 인공지능과 빅데이터를 통한 4차 산업혁명에 이르기까지 정수와 기하 없이는 한순간도 문명이 존재할 수 없다. 모두가 알고 있다고 느끼는 정수는 사실 놀랄 만큼 신비로운 대상인데, 매우 섬세하고 까다로워서 지난 수천 년간 인류역사상 가장 빛나는 지성들의 필사적인 노력에도 불구하고 부분적으로만 그 신비로운 자태를 드러냈을 뿐이다.
정수의 가장 기본적인 성질은 유일한 방법으로 소수들의 곱으로 쓸 수 있다는 것이다. 여기서 소수란 1과 자신 이외의 어떤 자연수로도 나눠지지 않는 1보다 큰 자연수를 말한다. 예를 들어 2, 3, 5, 7은 소수고 4나 6은 각각 2와 2, 2와 3의 곱이므로 소수가 아니다. 따라서 소수들을 모두 알면 정수에 대해 많은 정보를 얻을 수 있는데, 어린 시절 수학에 관심이 있었던 독자라면 소수가 아닌 수들(2의 배수, 3의 배수, 5의 배수 등등)을 차례로 지워가며 소수들의 목록을 만들어 본 기억이 있을 것이다. 이러한 경험을 통해 추측하고, 배중률의 교과서적 사례인 유클리드의 증명을 통해 알 수 있듯이 소수들의 집합은 무한하다. 여기까지만 알아도 많은 질문을 던질 수 있다. 3과 5, 11과 13과 같이 차이가 2인 소수들의 쌍이 무한히 많은가(쌍둥이 소수 추측), 주어진 자연수를 소수들의 곱으로 분해하는 효율적인 방법은 무엇인가(P=NP 문제), 4 이상의 짝수를 두 소수의 합으로 쓸 수 있는가(골드바흐의 추측) 이와 같은 질문을 스스로 생각했다면 수학적 재능이 매우 뛰어난 사람이다. (좋은 질문을 던지는 것이 학문의 반이고 올바른 각도에서 질문을 던지면 증명이나 답은 대부분 자연스럽게 나온다.) 위의 문제들은 모두 미해결이고 하나라도 해결할 수 있다면 인류문명이 존재하는 한 불멸의 영광을 누릴 수 있을 것이다.
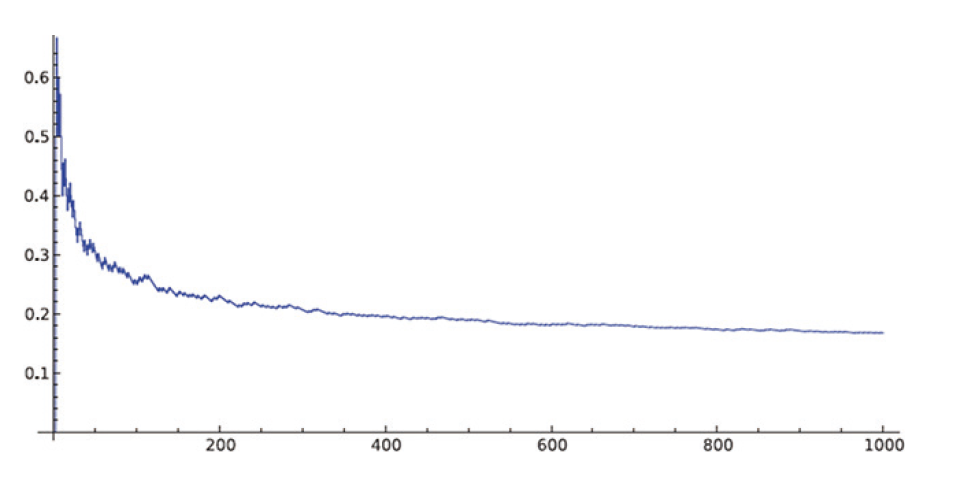
소수들을 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,‧‧‧ 과 같이 차례로 나열해 보자. 수천 년 동안 많은 사람들이 이 소수의 수열에서 규칙성을 발견하고자 노력했는데 아무도 성공하지 못했다. 소수는 비온 뒤 잡초가 자라는 것처럼 불쑥불쑥 나타나고 어떤 법칙도 따르지 않는 것으로 보인다. 소수들은 어떠한 제어도 거부하며 말 그대로 제멋대로다. 그럼에도 불구하고 19살의 가우스Carl Friedrich Gauss, 1777~1855는 많은 소수를 손으로 계산해 깜짝 놀랄 만한 관찰을 했는데, 난공불락의 임의성을 가지는 소수들이지만 이들의 통계적 분포는 엄청난 규칙성을 띠고 있다는 것이다. 10 이하의 자연수 중에서 소수는 몇 퍼센트를 차지하는가? 4개 있으므로 40%. 100 이하 소수는? 25개 있으므로 25%. 1000 이하의 소수는? 168개를 얻었는가? 16.8%. 백만 이하의 소수는? 약 7.85%임을 확인할 수 있다. 어린 가우스가 먼저 확인한 것은 x이하의 자연수 중에서 소수의 개수를 p(x)라고 두면 소수가 차지하는 비율 p(x)/x이 x가 커짐에 따라 감소한다는 것이었다. 천재적인 수학자인 가우스는 여기서 한 걸음 더 들어간다. (가우스에게 있어선 작은 발걸음이지만, 인류 전체에 있어선 커다란 도약인 것이다.) 그렇다면 어떤 형태로 감소하는가?
통제 불능의 소수들이 기적적으로 거의 미끈한 곡선으로 나타나는 것이 보이는가? 10대의 가우스는 일곱 자릿수까지의 로그 값이 들어있는 표를 들고 p(x)/x의 그래프가 1/log(x)의 그래프와 거의 같음을 순수한 손 계산으로 관찰했다. (로그 log(x)는 오일러 상수를 밑으로 하는 지수함수 exp(x)의 역함수이다) 즉 가우스의 추측은 ‘p(x) ~ x/log(x)’라는 것이다. 여기서 ‘~’는 가깝다는 뜻으로 정확히는 둘의 차이를 x로 나누면 x가 커짐에 따라 0으로 수렴한다는 의미다.
리만Bernhard Riemann, 1826~1866은 40년이 안 되는 짧은 생애를 통해 책 한 권 엮을 분량도 안 되는 업적을 남겼지만, 그의 논문 한 편 한 편은 해당 분야 학문의 주춧돌을 새로 놓는 기념비적인 성과가 된 유일무이한 천재다. (리만이 60세까지 살았더라면 지금 세상은 어떤 모습일까?) 현재 미적분학 시간에 배우는 리만 적분의 이론을 정립해 해석학에 기여했고 복소수 함수의 미적분학을 혁명적으로 발전시켰으며 이를 기하학적으로 접근해 복소대수기하학의 아버지가 됐다. 지도교수인 가우스의 요구에 못 이겨 쓴 박사학위 논문에서는 놀랄 만큼 유연한 새로운 기하학(당연히 리만 기하학!)을 창안했고 이것이 반세기 후 아인슈타인의 일반상대성 이론의 모태가 된 것은 잘 알려진 사실이다. 1859년 리만은 해석적 방법을 통해 지도교수인 가우스의 추측을 증명하고자 했는데, 리만 제타 함수의 근들이 예상되는 곳에만 있으면 소수의 분포에 관한 가우스의 추측이 사실임을 보였다. 여기서 리만 제타 함수란
\(\zeta (s)=\sum _{ n\ge 1 }^{ }{ \frac { 1 }{ { n }^{ s } } } =\prod _{ p:소수 }^{ }{ \frac { 1 }{ 1-{ p }^{ -s } } }\)
로 정의되고 리만 가설이 주장하는 바는 이 함수의 근들이 음의 짝수가 아니면 실수부가 1/2인 복소수라는 것이다. (정확히 말하자면 우변은 실수부가 1보다 큰 데서만 수렴하므로 이를 해석적으로 확장해 1이 아닌 복소수 전체에서 정의된 함수로 만들고 나서 근을 찾는 것이다.)
가우스의 추측과 리만 가설은 곧 19세기 수학자들의 성배가 됐고 이를 증명하면 불멸의 영예를 얻을 수 있음이 명백해졌다. 20세기 직전에 이르러 아다마르Jacques Hadamard, 1865~1963와 발레 푸쌩Charles Jean de la Vallee Poussin, 1866~1962이 리만 가설보다는 약하지만 가우스의 추측을 증명하기엔 충분한 만큼만 제타 함수의 근의 분포에 관한 사실을 증명했고 이후 가우스의 추측은 소수 정리라고 불린다. 하지만 리만 가설 자체에 대해서는 수없이 많은 실험적 결과(10조 개의 근들에 대해 참임이 확인됐다)에도 불구하고 실패한 시도만 무수히 쌓일 뿐, 엄밀한 증명은 요원하기만 하다.
1900년 세계수학자대회에서 힐버트David Hilbert, 1862~1943는 역사적인 강연을 통해 20세기 수학의 방향을 결정지은 23개의 문제를 제시했는데 여기서 리만 가설이 8번째 자리를 차지했다. 다시 백 년이 지나 2000년 미국 클레이 연구소에서 각각 백만 불의 상금이 걸린 7개의 수학 문제를 제시했는데 리만 가설이 이 중 하나다. 20세기 말 정보통신혁명 과정에서 소수들이 결정적인 역할을 했는데(어딘가에 비밀번호를 넣고 로그인할 때마다 큰 소수가 뽑혀서 곱해지곤 한다) 소수들의 분포를 보다 정확히 알 수 있다면 큰 변화를 이끌 수 있다. 따라서 리만 가설은 시간이 지날수록 그 중요성이 더해가고 있으며 대부분의 수학자는 리만 가설이 수학에서 가장 중요한 문제라는데 이의를 달지 않을 것이다. 당연히 리만 가설의 증명에는 수없이 많은 실패한 시도들이 있었고 이 중 대부분은 아마추어 수학자들의 도전으로, 아무 관심을 끌지 못한 채 버려지곤 한다. 하지만 저자가 전문적인 훈련을 받은 수학자라면 특히 평범한 수학자가 아닌 위대한 마이클 아티야라면 경우가 다를 수밖에 없다.
마이클 아티야
20세기 들어 수학은 혁명적 발전을 거듭했는데, 대표적으로 20세기 초 추상대수와 미분기하학의 발전, 20세기 중반 위상수학의 눈부신 성장, 후반 대수기하학의 거듭된 혁신, 20세기 말 응용수학의 도약 등을 들 수 있겠다. 20세기 후반 이러한 혁명의 중심에 서서 선도해온 위대한 수학자가 바로 마이클 아티야 경이다.
아티야는 천부적인 기하학자다. 레바논계 아버지를 둔 영국인인 아티야는 1929년 영국에서 태어났지만 어린 시절을 수단과 이집트에서 보냈고 많은 나라를 여행할 수 있었다. 자신의 수학적 재능을 깨달은 후 케임브리지대에서 공부하고 당대 영국을 대표하는 기하학자인 호지Sir William Hodge, 1903~1975의 지도하에 대수기하학을 연구해 1955년 박사학위를 받았다. 이후 미국 프린스턴 고등연구원을 1년간 방문해 뛰어난 동료들을 만났는데 이들과 함께 20세기 후반 세계 수학계를 선도했다.
50년대 말까지는 대수기하학 연구를 계속했는데 타원곡선상의 벡터번들을 분류하는 문제에 도전했고 이를 멋지게 해결해 떠오르는 스타로서 각광받기 시작했다. 50년대 말 히르쩌부르흐Friedrich Hirzebruch, 1927~2012의 초청을 받아 독일 본을 방문했는데 황금 세대를 구가하던 위상수학자들과 교류하는 과정에서 그로덴틱Alexander Grothendieck, 1928~2014의 리만-로흐 정리의 증명에서 받은 영감을 바탕으로 히르쩌부르흐와 함께 공간의 특성을 표현하는 새로운 방법인 K-이론을 제시했다. 이후 K-이론을 발전시키고 이를 통해 미해결 문제들을 다수 해결하는 쾌거를 이뤄냈다. 이 업적을 인정받아 1966년 37세의 나이에 수학계 최고의 상인 필즈상을 수상했다.
1960년대 중반 아티야는 싱어Isadore Singer, 1924~와 함께 그의 가장 유명한 업적 중의 하나인 아티야-싱어 지표 이론을 개발했다. 대수적으로 확립된 그로덴틱-리만-로흐의 정리를 더 일반적인 공간으로 확장했는데 이는 기하학을 넘어서 이론물리학에 강력히 응용됐다. 아마 이 과정에서 물리학자들과의 교류가 시작됐을 것으로 보이는데 1970년대 후반부터는 미분기하학의 한 분야인 게이지 이론을 발전시켰고 이는 도널슨Sir Simon Donaldson, Fields Medal 1986의 4차원 다양체 이론과 위튼Edward Witten, Fields Medal 1990의 초끈이론과 양자장 이론 연구에 기여했다. 이러한 업적을 인정받아 2004년 아벨상을 싱어와 공동수상했다.
달변인 아티야는 행정적으로도 탁월하여 옥스퍼드대 수학과를 성공적으로 이끄는 한편 영국수학회, 영국왕립학회의 회장을 성공적으로 역임했고 뉴튼 수학연구소를 열고 초대소장을 맡았으며 케임브리지 트리니티 칼리지 학장으로 재직하는 동안에도 학생들의 존경과 사랑을 받았다. 또한 학생들을 지도하는 데도 탁월해 도널슨, 히친Nigel Hitchin, 커원Dame Frances Kirwan과 같이 기라성 같은 제자들을 길러냈다. 1983년 기사 작위를 받았고 1992년 메리트 훈위Order of Merit의 회원이 됐다.
수학자로서 무엇 하나 흠잡을 데 없이 완벽한 아티야는 20세기 후반 많은 수학자들의 귀감이 됐으며 필자가 가장 존경하는 영웅으로 꼽는 위대한 학자다. 고도로 훈련된 수학자만이 이해할 수 있을 정도로 어렵고 허락된 지면의 크기가 너무 작아 아티야의 업적들을 더 잘 설명할 수 없음이 안타깝다. 개인적으로는 박사과정 초기에 아티야와 보트의 양-밀즈 방정식에 관한 기념비적인 논문을 한 단어씩, 한 줄씩 힘겹고 끈질기게 읽는 과정을 통해(눈앞의 한 구절의 해석에 자신의 운명이 걸려있다고 확신할 수 없는 자는 학문의 세계에 발들일 꿈도 꾸지 말지어다) 큰 배움을 얻었고 제자인 커원 교수와 오랜 공동연구를 통해 그의 옷자락이 스친 여운을 느낀 바 있다.
아티야의 증명
지난 9월 말 독일 하이델베르그에서는 제6회 수상자 포럼이 열렸는데 이는 필즈상, 아벨상, 튜링상, 네반린나상을 받은 저명한 수학자들이 자신의 경험과 지식을 젊은 세대와 공유하는 특별한 자리다. 놀랍게도 아티야 경은 여기서 리만 가설을 증명했다고 발표했고 전례 없는 언론의 관심을 끌었다. 유튜브를 통해 그 강의를 누구나 볼 수 있으며 아티야의 5쪽짜리 짧은 논문은 인터넷을 통해 확인할 수 있다.
통상의 수학적 기준으로 아티야 교수의 논문은 논문이라고 부를 수 없고 증명이라고 하기에 구멍이 너무 많다. 보통 수학 논문은 언제 어디서 어떤 공격이 들어오더라도 막아낼 수 있을 정도로 빈틈없이 탄탄하게 구성해 읽는 사람이 누구건 받아들일 수밖에 없도록 쓴다. 단어 하나하나의 의미를 따지고 또 따지며 쉼표 하나도 함부로 찍지 않는다. 100가지를 알고 있는 경우에도 완벽하게 방어할 수 있는 10가지만 적는 것이 통상적인 관례고 그래서 수학적인 결과들은 한번 받아들여지면 여간해선 뒤집히는 일이 없다. 아티야 교수의 예전 논문은 수학 논문의 교본으로 삼아도 될 만큼 명문이었고 치밀하고 꼼꼼하면서도 수려한 흐름으로 늘 감동을 줬다. 따라서 아티야 교수의 지난달 강연과 논문에 대해 의견을 낼 필요도 느껴지지 않는다. 하지만 의문은 남는다. 도대체 무슨 의도로 쓴 글이며 왜 하필 하이델베르그 수상자 포럼같이 중요한 자리에서 발표한 것일까?
세 가지 가능성을 생각해 본다. 첫째, 노학자의 지적 능력 상실이다. 그를 영웅으로 품고 살아온 후학이 받아들이기엔 너무 슬프다. 둘째, 노학자의 초월이다. 통상적 기준이 더 이상 의미가 없고 기존의 학문적 문법을 넘어선 사유가 가능한 경지에 도달하신 것은 아닐까? 셋째, 노학자의 격려다. 논문의 4쪽에 페르마의 무한강하법과 자신의 증명을 비교하는 대목이 나온다. 페르마Pierre de Fermat, 1607~1665가 자신이 읽던 책의 한 귀퉁이에 자신이 놀랄만한 증명을 얻었으나 여백이 없어 적지 못한다고 쓴 것이 350년 동안 수학자들을 자극하여 결국에는 와일즈Andrew Wiles, 1953~의 장엄한 증명을 이끌어낸 바 있다. 어느 쪽이 진실인가? 답은 아티야 교수만이 알고 있을 것이다. 분명한 것은 이번 해프닝이 아티야 교수의 위대한 수학적 성취에 조금의 흠집도 낼 수 없을 정도로 그가 찬란한 삶을 살았다는 점이다.
수학자들이 리만 가설을 얼마나 사랑하는지 보여주는 일화로 이 글을 맺고자 한다. 20세기 초반 영국의 수학자 하디Godfrey Harold Hardy, 1877~1947가 덴마크 방문을 마치고 영국으로 귀국하던 날 파도가 거세 배를 타기에 매우 위태로워 보였다. 아마도 배를 타고가다 죽을 것이라 생각한 하디는 승선 직전 동료 수학자에게 전보를 쳤다. “리만 가설을 증명했음.”
본 글은 서울대학교 대학신문 1973호(2018년 11월 5일자)에 실렸던 기사입니다.