2018년 세계수학자대회에서 필즈상 수상자가 발표된 직후, 수상자 중 한 명인 악샤이 벤카테슈Akshay Venkatesh에 관한 글을 HORIZON에 기고해달라는 의뢰가 왔다. 원고 의뢰를 받고 나니 대학원생 시절 지도교수의 추천으로 벤카테슈의 박사논문을 붙잡고 몇 주간 낑낑대던 기억이 떠올랐다. 필자와 벤카테슈는 같은 지도교수 아래에서 박사학위 지도를 받았기 때문에, 대학원생 시절부터 벤카테슈에 대한 이야기를 들을 일이 종종 있었다. 물론 벤카테슈와 직접 만나 이야기를 나눌 기회가 찾아온 것은 비교적 나중의 일이다. 평소 가장 존경하는 동시대 수학자 중 한 명이 벤카테슈였던 터라 바로 원고 의뢰를 수락하였다. 이제부터 필자가 바라보는 벤카테슈의 수학과 그와 관련된 이야기를 풀어놓고자 한다.
The Simons Foundation, IMU
벤카테슈 교수의 이력
벤카테슈 교수의 어린 시절은, 영재를 주인공으로 하는 소설일지라도 현실성이 없다고 지적받을 만큼 화려하다. 1981년 인도에서 태어난 벤카테슈는 2살 때 가족과 함께 호주 퍼스Perth로 이민을 가게 된다. 보통 고등학생들이 참가하는 국제물리올림피아드와 국제수학올림피아드에, 벤카테슈는 각각 만 11살과 12살일 때 호주 대표로 참가하여 두 번 모두 동메달을 수상하였다.1 이후 13살 때 서호주대학University of Western Australia에 최연소 학생으로 입학하였고, 16살 때 프린스턴 대학Princeton University에서 박사과정을 시작하여, 20살이 되던 해인 2002년 피터 사르낙Peter Sarnak교수의 지도로 수학 박사 학위를 취득하였다. 그후 MIT, 뉴욕대학NYU, 고등과학원Institute for Advanced Study, 스탠포드 대학Stanford University 등 이름만 들어도 엄청난 연구기관과 대학들을 거쳐 올해 8월부터 미국 프린스턴에 위치한 고등과학원에서 영년직 교수로 재직 중이다.
올라운드 수학자
벤카테슈의 수학을 간단히 설명하는 것은 쉽지 않은 일이다. 벤카테슈의 대단함은 그가 분야 경계가 없는 수학을 한다는 점에 있기 때문이다. 국제수학연맹 역시 벤카테슈의 필즈상 수상 사유로 정수론, 동역학, 표현론, 산술기하학 등을 넘나들며 많은 미해결문제를 풀었다는 점을 들었다. 연구에 사용하는 기술의 범주도 매우 넓은 편이어서, 벤카테슈야말로 진정한 의미로 올라운드 수학자라고 말할 수 있다. 이 글에서는 그가 지난 20여 년간 발표한 40편이 넘는 논문 결과 중, 동역학과 정수론에 관련된 이야기를 하고자 한다. 이것은 결코 위상, 표현론 등을 포함한 다른 분야에서 벤카테슈가 이뤄낸 결과가 덜 중요하다는 것이 아니라, 단순히 필자의 취향에 의해 결정된 부분임을 미리 밝혀둔다.
삼각형 당구대
처음으로 소개하고 싶은 벤카테슈의 업적은 닫힌 궤적periodic orbit에 관한 것이다. 예컨대 직사각형 당구대에서의 닫힌 궤적이란, 마찰이 없는 상태에서 공이 일정 시간을 주기로 같은 궤적을 따라 움직이고 있다고 할 때의 궤적을 뜻한다.
위의 경우만 하더라도 수많은 종류의 서로 다른 닫힌 궤적들이 있음을 쉽게 알 수 있지만, 정작 이 닫힌 궤적들이 어떻게 분포하는지 아는 것은 쉬운 일이 아니다. 벤카테슈는 [1]에서 이러한 닫힌 궤적들의 분포를 \(\operatorname{SL}_n(\mathbb{Z}) \backslash \operatorname{SL}_n(\mathbb{R})\)이라는 공간에서 연구한다.2
\(n\)이 \(2\)인 경우에는 닫힌 궤적들의 분포에 관해 다양한 결과가 알려져 있지만, \(n\)이 \(3\)이상인 경우에는 문제의 복잡도가 엄청나게 올라가서 벤카테슈의 이 결과가 있기 전에는 알려진 게 많지 않았다(예컨대 \(n\)이 \(3\)인 경우 이 공간은 \(8\)차원이다!). 이 결과는 “Higher Rank Homogeneous Dynamics”라는 동역학의 한 분야에 크게 기여했다는 평을 받는다.
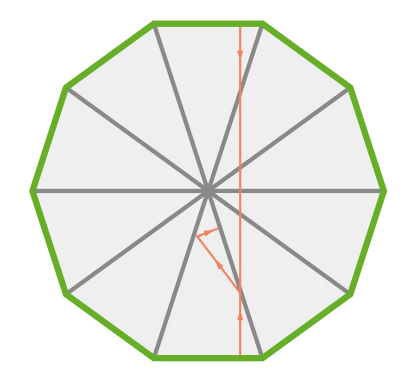
조금 더 직관적으로 벤카테슈가 논문[1]에서 다루고 있는 문제를 이야기하기 위해 삼각형에서의 닫힌 궤적을 살펴보고자 한다. 삼각형 안에서 자유입자가 변과 변 사이를 튕기며 그리는 궤적을 이해하는 것조차 수학적으로 쉽지 않은 문제이다. 우선 세 각이 \(36\), \(72\), \(72\)도인 이등변 삼각형을 생각해보자.
이 삼각형은 다른 삼각형들과 달리 특이한 성질이 하나 있는데, 밑변에서 중점과 양 끝점을 제외한 점에서 수직으로 자유입자를 쏘면, 다른 두 변에 일정 횟수를 튕긴 후 반드시 제자리로 돌아오게 되어있다는 점이다.
즉 이 경우엔 무한히 많은 닫힌 궤적들을 찾을 수 있고, 삼각형 위의 거의 모든 점에서 그 점을 지나는 닫힌 궤적을 찾을 수 있다.
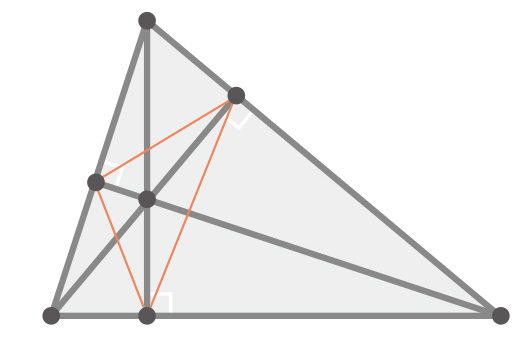
일반적으로 예각 삼각형의 경우 수심3에서 각 변에 내린 수선의 발을 연결하여 얻어진 수심 삼각형이 닫힌 궤적이 됨을 알 수 있다. 이를 제외하고도 많은 닫힌 궤적들을 찾을 수 있음이 알려져 있고, 특수한 경우엔 닫힌 궤적의 정량적 분포에 대해 이야기하는 것도 가능하다.4
이와는 대조적으로 둔각삼각형의 둔각이 \(100\)도보다 큰 경우에는, 몇몇 특수한 경우를 제외하고는 닫힌 궤적을 단 하나라도 찾을 수 있을지에 관해 알려진 바가 없다. 어떻게 접근해야 풀 수 있는 문제인지 어떤 수학자도 감을 잡지 못하고 있는 것이다.
이처럼 닫힌 궤적들의 분포를 이해하는 문제는 삼각형에서조차 어려운 문제인데, \(SL_n(\mathbb{Z}) \backslash SL_n(\mathbb{R})\)이라는 거대한 공간에서 문제의 답을 얻어낼 수 있었으리라 누가 쉽게 이야기할 수 있었을까.
바둑판과 동역학
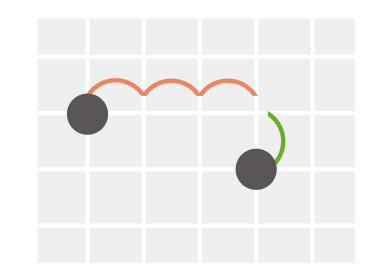
두 번째로 다룰 벤카테슈의 업적은 동역학에서 다뤄지는 여러 정량적인 결과를 정수론에 적용했다는 점이다. 정량적인 동역학 문제가 무엇인지에 대해 먼저 이야기해보겠다. 만약 근처에 바둑판과 바둑알이 있다면 이 글을 읽으며 직접 해보는 것을 추천한다. 우선 바둑판의 가장 아래 줄에 \(19\)개의 바둑알을 일렬로 채워 넣는다(즉, \(18\times 19\) 크기의 바둑판을 만든 셈이다). 그리고 아무 점이나 하나 골라 바둑알을 하나 두자. 그다음부터는 다음과 같은 작업을 반복하면서 바둑알을 놓기로 한다.
이 작업을 반복하다 보면 가는 곳마다 이미 바둑알이 놓여 있어서 더 이상 새로운 바둑알을 놓을 수 없을 때가 생길 것이다. 과연 이때 바둑판은 꽉 차 있을까? 만약 아래로 세 칸, 오른쪽으로 한 칸 가는 것으로 규칙을 바꾸면 결과가 어떻게 될까? 일반적으로 오른쪽으로 \(n\)칸 아래로 \(m\)칸 간 다음에 바둑알을 내려둔다면, \(n\)과 \(m\)의 값에 따라 결과가 어떻게 바뀔까? 또한 바둑판의 크기가 달라지면 어떻게 될까?
벤카테슈의 업적에 관해 이야기하기 위해선 조금 더 복잡한 질문을 해야 한다. 똑같은 작업을 반복하며 바둑알을 놓는데, 이번에는 바둑알이 \(150\)개밖에 없다고 가정하자. 처음 \(18\times 19=342\)개의 점이 비워져 있었으므로 바둑알이 대략 절반에 못 미치는 개수다. 그렇다면 \(150\)개를 전부 내려놓았을 때, 바둑알이 전혀 놓이지 않은 \(3\times 3\) 사각형이 있을까? \(3\times 3\) 사각형을 찾기 위해선 \(9\)개의 빈 점이 필요하니, 바둑알 \(150\)개를 모두 놓았을 때도 빈 점이 \(192\)개임을 고려하면 반드시 없다고 이야기하기 어려워 보이지 않는가? 하지만 실제로 해보면 없음을 알 수 있다.
이 맥락에서 물어볼 수 있는 가장 어려운 부류의 질문은 다음과 같다.
이것은 결국 언젠가는 바둑판을 다 덮는 걸 알지만, 정량적으로 얼마나 고르게 덮이고 있는지 이해하는 문제의 일종이라고도 볼 수 있다.
수학은 때로 아주 단순한 관찰이 큰 발전을 가져다주기도 하는데, 벤카테슈는 서술하는 것조차 난해한 현대의 해석적 정수론 혹은 표현론에 등장하는 특정한 형태의 적분들5과 위에서 언급한 문제들의 단순하지만 깊은 상관관계를 처음으로 관찰해낸 사람이다.[2] 단편적으로 이 상관관계는 얼마 안 가 해석적 정수론의 난제 중 하나였던 “Subconvexity Problem for \(\operatorname{GL}_2\)”를 해결하는데[3] 도움이 되기도 하였고, 최근에는 [2]에 쓰인 아이디어 이용하여 표현론에서 등장하는 Gan-Gross-Prasad 가설을 연구하는 움직임도 있다.
맺는말
이 글에서는 벤카테슈의 업적들을 간략하게 소개하였다. 하지만 벤카테슈가 정말 훌륭한 수학자인 이유는, 여러 분야에 걸친 그의 결과들이 보여주듯, 분야에 대한 편견 없이 수학을 해왔던 점임을 강조하고 싶다. 그의 수학적 깊이는 단순히 이해력이 뛰어나기만 해서는 이룰 수 없고, 끊임없이 다양한 분야의 새로운 수학들을 장시간 섭렵해야 다다를 수 있는 경지이다. 그의 필즈상 수상을 진심으로 축하하는 마음이다.
참고문헌
- M. Einsiedler, E. Lindenstrauss, P. Michel, and A. Venkatesh, Distribution of periodic torus orbits on homogeneous spaces, Duke Math. J., 148(1):119–174, 2009.
- A. Venkatesh, Sparse equidistribution problems, period bounds and subconvexity, Ann. of Math. (2), 172(2):989–1094, 2010.
- P. Michel and A. Venkatesh, The subconvexity problem for \(\operatorname{GL}_2\), Publ. Math. Inst. Hautes Études Sci., (111):171–271, 2010.