4월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
4월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 김일희님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
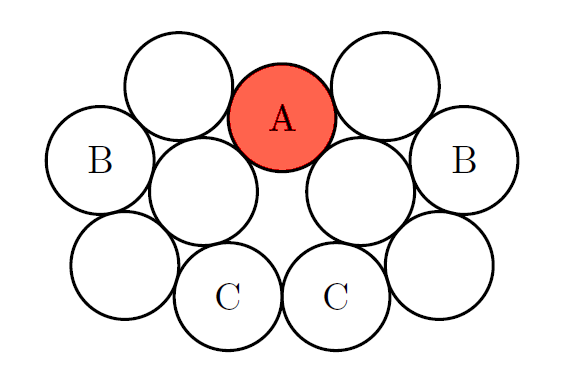
다음 그림과 같이 배치하면 칩 11개로 네 개의 색이 필요하게 만들 수 있다. 만약 이 칩들을 세 가지 색으로 모두 칠했다면, A 칩이 빨간 색일 때, 인접한 칩에 어떤 것을 놓더라도 B 칩은 빨간 색이어야 한다. 같은 식으로 C 칩 또한 빨간 색이 되어 서로 맞닿은 두 C 칩이 모두 빨간 색이 된다.
이 문제는 미국 스톡턴 주립대의 데이비드 해머David Hammer가 1975년에 학술지 American Mathematical Monthly에 제출한 문제였고, 풀이는 1976년 6호에 실렸다. 이 문제는 마틴 가드너Martin Gardner의 Scientific American 칼럼에도 소개되었다.
다음은 4월의 정답자로 선정된 김일희님의 해설입니다.
답 : 11개
풀이 :
반드시 4개의 색이 필요한 가장 작은 칩들의 덩어리 예제를 G라고 하고, G의 특성을 파악해 봅시다.
㉠. G 보다 칩이 적으면 3가지 색으로 칠할 수 있습니다.
– 칠할 수 없다면 4색이 필요한 더 작은 예제가 있다는 말이니까 G의 정의에 모순입니다.
㉡. G 의 각 칩은 적어도 3개 이상의 다른 칩들과 접하고 있습니다.
– 만약 2개 이하의 칩과 접하는 칩이 있다고 가정해 봅시다. ㉠에 의해 그 칩을 빼고 남은 전체덩어리를 3색으로 칠할 수 있습니다. 제거한 칩과 원래 접해있던 2개 이하의 칩에 칠해져 있지 않은 남은 색으로 제거된 칩을 칠함으로써 원래 덩어리를 3색으로 칠할 수 있게 됩니다. 이는 G 를 칠하는데 반드시 4색이 필요하다는 사실에 모순이므로, G에는 2개 이하의 칩과 접하는 칩이 없다는 사실을 알 수 있습니다.
㉢. G 에서 아무 칩 하나를 빼 내더라도 여전히 나머지 칩 덩어리는 연결되어 있습니다.
– 만약 그렇지 않고 덩어리가 분리가 된다고 해봅시다. 분리된 덩어리를 각각 A, B, 빼 낸 칩을 v라고 해 봅시다. ㉠에 의해 A와 v 를 합친 덩어리를 3색으로 칠할 수 있고, 마찬가지로 B와 v를 합친 덩어리를 3색으로 칠할 수 있습니다. 일반성을 잃지 않고, 두 컬러링에 v에 칠해진 색이 같다고 가정해도 됩니다. 이제 두 컬러링을 합치면 전체 덩어리를 3색으로 칠한게 되어 모순이므로, ㉢이 성립함을 알 수 있습니다.
㉣. G 에서 서로 접하고 있는 두 칩을 제거해도 여전히 나머지 칩 덩어리는 연결되어 있습니다.
– 만약 그렇지 않고 덩어리가 분리된다고 해봅시다. ㉢ 을 보인 논리와 비슷하게, 제거한 두 칩과 한 덩어리를 3색으로 칠하고, 역시 제거한 두 칩과 다른 덩어리를 3색으로 칠한 뒤, 두 컬러링을 합쳐서 전체 덩어리를 3색으로 칠할 수 있게 되어 모순입니다. 따라서 ㉣ 역시 성립합니다. (참고로 만약 두 칩이 접하고 있지 않으면, 같은 논리를 사용할 수 없습니다. 접해 있어야만 두 칩에 칠해진 색깔이 다르다는 것이 보장되므로, 두 컬러링을 합치는 것이 가능합니다.)
C를 G 덩어리 밖의 외부면과 접해있는 외부칩들만 모아놓은 덩어리라고 해 봅시다. (그림의 노란선 참고)
㉤. C 만 살펴보면 싸이클을 이루며, C의 각 칩은 C 안에서 바로 양 옆의 칩과만 접합니다.
– ㉢ 에 의해 C는 싸이클입니다. 그리고, C 의 어떤 칩 u가 C 안에서 바로 양 옆의 칩이 아닌 칩 v와 접한다면, u와 v를 제거하여 두 덩어리로 분리가 되기 때문에 ㉣에 모순입니다.
㉥. C 의 각 칩은, 적어도 하나의 내부 칩과 접합니다.
– ㉡ 에 의해 모든 칩은 3개 이상의 칩과 접해야 하는데, ㉤에 의해 C 안에서는 2개의 칩과 접합니다. 따라서, 적어도 하나의 내부 칩과 접해야 합니다.
㉦. 내부 칩의 갯수는 2개 이상입니다.
– ㉥ 에 의해 적어도 하나의 내부 칩이 있어야 합니다. 만약 내부 칩이 1개라고 하면, C의 모든 칩이 내부칩과 접하여야 하므로, 전체 덩어리가 7개가 됩니다. 그런데 이 덩어리는 3색으로 쉽게 칠할 수 있으므로 내부 칩은 2개 이상입니다.
㉧. 내부 칩의 갯수가 2개라고 하면, C 의 칩 갯수는 8 개 이상입니다.
– 내부 칩을 u, v 라고 해봅시다. u와 접하는 외부 칩은 path 를 이루고, v와 접하는 외부칩도 path 를 이룹니다. (그림의 빨간선 참고) 두 path 는 끝점을 공유하거나, 혹은 끝점끼리 접해있어야 합니다. 두 path 모두 안쪽에 한 점을 내부점으로 하기 위해서 길이가 4 이상이어야 합니다. 그리고, 6 이상일수도 없으므로 4 또는 5입니다. 적어도 한쪽 path 의 길이가 4 라면, 다른 path 와 끝점을 공유할 수 없고 접해야만 하므로, C의 길이는 최소 4 + 4 = 8 이상입니다. 두 path 의 길이가 모두 5라고 해도, C 의 길이는 최소 5+5 – 2 = 8 이상입니다.
㉨. 전체 칩의 갯수는 11개 이상입니다.
– 내부 칩의 갯수가 3개 이상이면 C의 길이가 9 이상이므로, 전체 칩의 갯수가 12개 이상입니다. 따라서, 내부칩의 갯수가 2개라고 가정해 봅시다. ㉧ 에 의해 칩의 갯수가 10개 이상이므로, 10개라고 가정해 봅시다. 그렇다면 ㉧ 에서 논의한 두 path 가 길이가 각각 5이고, 두 끝점을 공유하는 경우와 두 path 가 길이가 각각 4이고, 두 끝점이 접하는 경우가 가능합니다. 그런데, 두 경우 모두 3색으로 칠할 수 있는 것을 어렵지 않게 보일 수 있습니다. 따라서, 전체 칩의 갯수는 11개 이상입니다.
㉩. 그림의 예제가 4색이 필요한 가장 작은 예입니다.
이제 그림에서와 같이, ㉧ 에서 논의한 두 path 의 길이가 모두 5 이고, 한쪽 끝에서는 끝점을 공유하고 다른쪽 끝에서는 끝점이 접해있는 상황을 생각해봅시다. 이 경우, 칩의 갯수는 11개이고 3색으로 칠하는 것이 불가능합니다. 3색으로 칠해진다고 가정해보면, 두 path 가 공유하는 점에 칠해진 색과 path 의 반대쪽 끝점의 색이 같아야 하는데, 반대쪽 두 끝점이 접해있으므로 모순입니다. 따라서, ㉨에 의해 이 경우가 4색이 필요한 가장 작은 예입니다.