사교 위상수학1은 19세기 후반부터 급격하게 성장한 위상·기하학의 한 분야로 사교 다양체symplectic manifolds라고 불리우는 수학적 공간의 성질을 탐구합니다. 고전역학에서 동기를 얻어 성장한 사교 위상수학은 수학 여러 분야와 신비하게 얽혀 있어, 사교symplectic의 어원을 잘 설명하고 있습니다.2 [2] 우리가 태어나고 자라면서 자연스럽게 피부로 느껴온 공간을 연구하는 유클리드 기하학과 리만 기하학과는 달리,3 사교 위상수학은 처음 받아들이기에는 다소 생소하고 이질적인 공간을 다루고 있습니다. 이번 짧은 글을 통해 사교 다양체를 친근하게 알아가고 사교적symplectic 성질이 다른 분들께 조금이라도 마음에 와닿는 기회가 되길 바라봅니다.
리만이 도입한 다양체: 현대적인 수학적 공간
먼저, 2차원 공간을 이해하기 위해 온 인류가 옹기종기 모여 살고 있는 지구를 생각해봅시다. 우리가 지구 표면에서 차를 운전하여 자유롭게 여행을 떠나다 보면, 매번 어떤 곳에서든지 상하-좌우로 2차원만큼 움직일 수 있습니다.[그림1] (실제로는 여러 방해물들이 있을 수 있지만, 아무것도 없는 드넓은 들판만 계속 생긴다고 가정하겠습니다.)
도너츠 표면처럼 생긴 낯선 행성에서 운전을 할 경우에도
상하-좌우로 2차원만큼 자유롭게 움직일 수 있습니다. [그림2] 이처럼 2차원만큼 움직임의 자유도를 갖는 공간들이 2차원 곡면들의 예제이고, 이 개념을 고차원으로 확장한 것이 바로 다양체manifold입니다. 즉, 주어진 공간의 임의의 점에서 \(n\)차원의 방법으로 다양many하게 움직일 수 있으면, 그 공간을 \(n\)차원 다양체라고 합니다. 리만Riemann은 1854년에 다양체의 개념과 각도를 재는 도구를 도입하여, 그의 스승인 가우스Gauss와 함께 곡선의 길이와 공간의 굽어진 정도를 재는 곡률curvature과 같은 고유한 기하학적 성질들을 탐구하며 공간 연구의 현대적인 초석을 마련하였습니다.
사교 다양체의 기원: 고전 역학을 기술하는 수학적 공간
이제는 “사교 구조”를 갖고 있는 다양체인 사교 다양체가 무엇인지 알아보도록 하겠습니다.
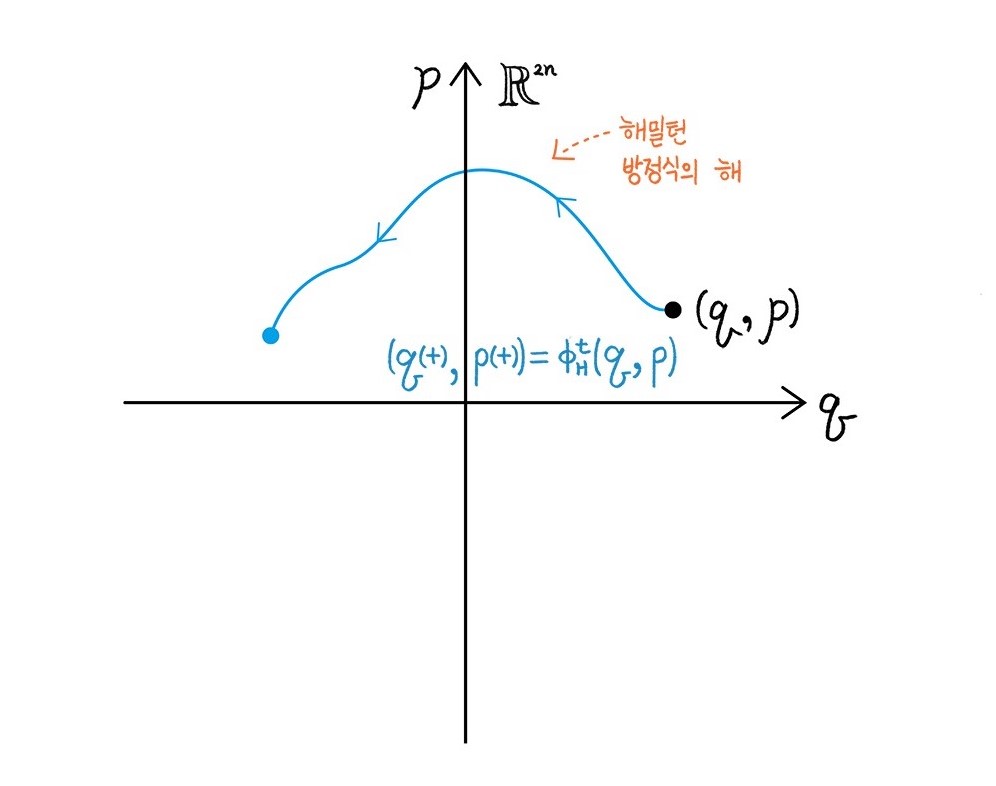
다소 엉뚱하게도 사교 다양체의 기원은 물체의 움직임을연구하는 고전역학과 깊은 관련이 있습니다. 거시적 관점에서 물체의 움직임을 이해하고 싶다면, 물체의 위치와 각각의 위치에서의 속도4를 기술해야합니다. \(n\)차원 다양체에서 움직이는 물체의 위치와 속력을 동시에 기록하기 위해서는 \(n+n=2n\)차원의 다양체가 필요할 것입니다. 즉, \(\mathbb{R}^n\) 공간에서 움직이는 물체의 역학은 \(\mathbb{R}^n\times \mathbb{R}^n=\mathbb{R}^{2n}\) 공간에 기술될 것입니다. 해밀턴 고전역학에 따르면, 시간 \(t\)에서 물체의 위치 \(q(t)\in \mathbb{R}^n\)와 속력 \(p(t)\in\mathbb{R}^n\)를 기술하기 위해 해밀토니안Hamiltonian \(H\colon \mathbb{R}^{2n}\to \mathbb{R}\)를 도입하면, 다음과 같은 연립 일계 미분방정식(해밀턴 방정식)을 얻게 됩니다:
\(\begin{cases}\dot{q}(t) = \frac{\partial H}{\partial p}(q(t),p(t)) \\\dot{p}(t) = -\frac{\partial H}{\partial q}(q(t),p(t))\end{cases}\)
이때, 해밀토니안 \(H(q,p)\)는 고려하는 역학 문제에 따라서 선택됩니다.
이제, 해밀턴 방정식의 해solution들을 모아 해밀토니안 흐름Hamiltonian flow \(\phi_H^t\colon \mathbb{R}^{2n}\to \mathbb{R}^{2n}\)을 얻어내고5, 이 흐름으로 역학계를 완전히 이해하는 방식이 바로 고전역학에서의 해밀턴 형식론입니다.
이제 비교적 잘 알려진 두 가지 역학계들을 살펴보겠습니다.
조화 진동자Harmonic oscillator
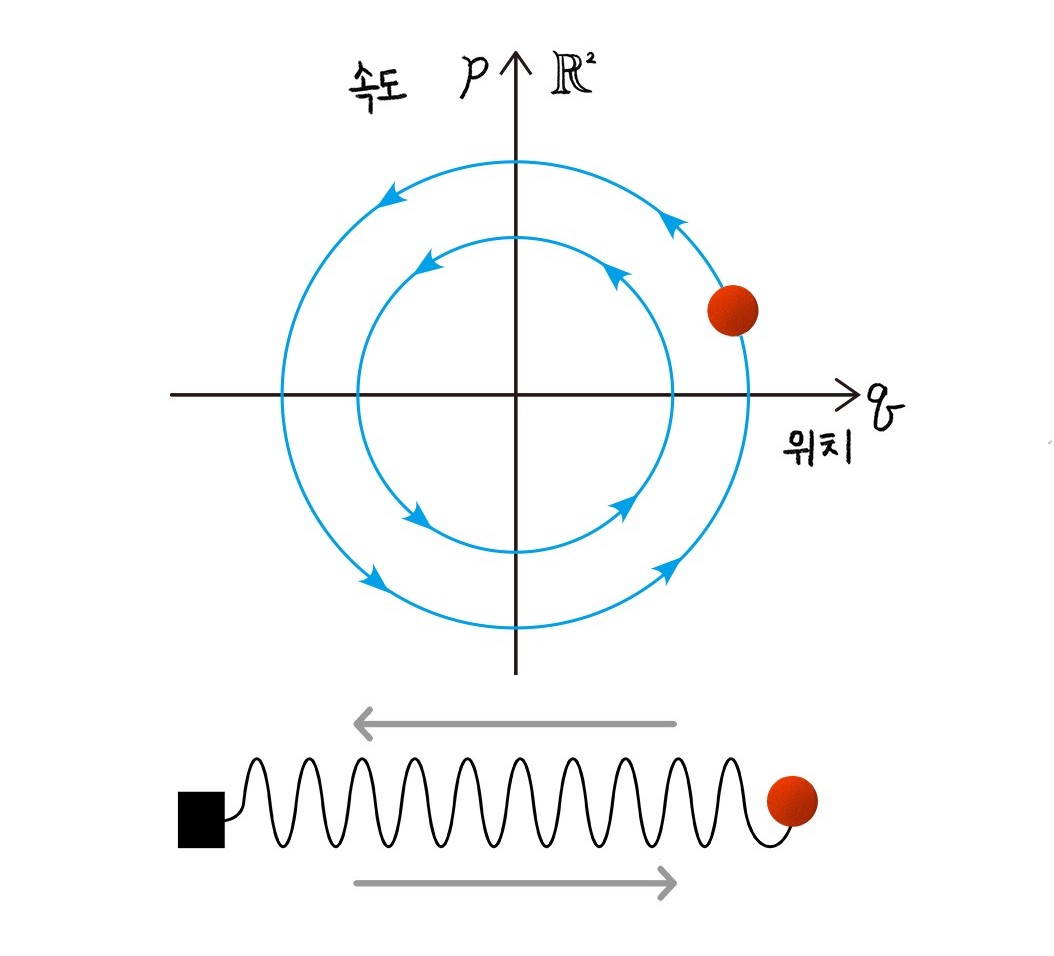
\(\mathbb{R}^2\)에 정의된 해밀토니안 \(H(q,p)=\frac{1}{2}|p|^2\)에 대해, 해밀턴 방정식의 해들은 원점을 중심으로 돌아가는 원들의 궤적을 그리고 있습니다. 이 해밀토니안은 훅Hook의 법칙에 의한 힘 이외에 다른 외력을 받지 않는 용수철의 주기적인 진동을 기술합니다.[그림4]
케플러 문제Kepler problem
\(\mathbb{R}^6=\mathbb{R}^3\times\mathbb{R}^3\)에 정의된 \(H(q,p)=\frac{1}{2}|p|^2 – \frac{1}{|q|}\)의 해밀토니안 흐름은, 우주의 해sun를 중심으로 돌아가는 행성들의 궤도를 케플러의 법칙에 따라 기술합니다.
주어진 해밀토니안에 대해 (연립 일계 미분방정식이라 할지라도) 해밀턴 방정식을 완벽하게 푸는 것은 매우 어렵기 때문에, 해밀토니안 흐름이 보편적으로 보존하는 성질과 양을 찾아내어 역학계를 이해하는 방법이 매우 중요합니다.
리우빌Liouville 정리
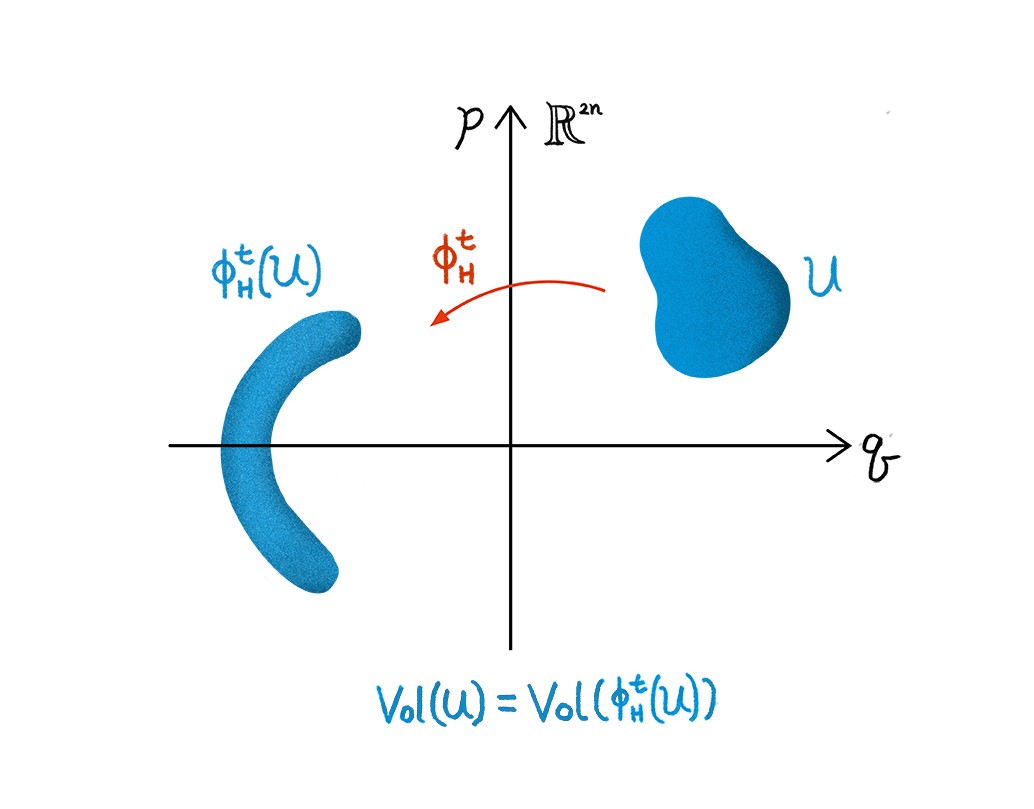
\(\mathbb{R}^{2n}\)에 정의된 유클리드 \(2n\)차원 부피는 해밀토니안 흐름 \(\phi_H^t\colon \mathbb{R}^{2n}\to \mathbb{R}^{2n}\)에 대해 불변합니다. 즉, \(\mathbb{R}^{2n}\) 공간의 임의의 열린 집합 \(U\)과 모든 \(t\)에 대해서, \(\text{Vol} (U)=\text{Vol}(\phi_H^t(U))\)를 만족합니다.[그림5]
부피보다 더 섬세한 보존량은 푸엥카레에 의해 1901년에 발견되었습니다.
푸엥카레Poincaré 정리
해밀토니안 흐름 \(\phi_H^t\colon \mathbb{R}^{2n}\to \mathbb{R}^{2n}\)은 미분 형식differential form
\(\omega_0=\displaystyle \sum_{i=1}^n dx_i\wedge dy_i\)을 보존합니다.
미분 형식 \(\omega_0\)을 쉽게 설명하면, \(\mathbb{R}^{2n}\) 공간 속에 있는 2차원 곡면들의 면적를 잴 수 있게 해주는 도구로 이해할 수 있습니다.6
푸엥카레의 정리에 따르면, 해밀토니안 흐름이 2차원 곡면들의 면적를 보존한다는 사실을 얻게 됩니다. 또한, 2차원 곡면이 \(n\)번 곱해지게 되면 \(2n\)차원의 다양체가 되기 때문에, \(2n\)차원 다양체의 부피도 보존이 된다는 리우빌 정리를 유도할 수 있습니다. 더 놀라운 관찰은 미분 형식 \(\omega_0\)를 이용하여 \(\mathbb{R}^{2n}\)에서 정의된 해밀턴 방정식을 특수한 벡터장에 접하는 곡선의 방정식으로 이해할 수 있게 된다는 것입니다. 이러한 벡터장을 해밀턴 벡터장이라고 부르는데,7 해밀턴 벡터장을 정의하기 위해서는 푸엥카레 미분 형식 \(\omega_0\)의 중요한 성질인 비퇴화성non-degeneracy이 필요합니다.8 이제, 해밀턴 벡터장을 적분하면 해밀토니안 흐름을 얻게 되는데, 이는 해밀턴 방정식을 풀어서 해밀토니안 흐름을 얻었던 과정과 동일합니다. 푸엥카레 정리에서 해밀토니안 흐름이 2차원 곡면들의 면적를 보존한다는 사실은 미분 형식 \(\omega_0\)의 닫힘성closedness이라는 성질로 기인한 것입니다.9 지금까지 관찰한 푸엥카레의 미분 형식 \(\omega_0\)의 두 가지 중요한 성질인, 비퇴화성과 닫힘성을 갖는 미분 형식 \(\omega\)를 사교 구조symplectic structure라고 부릅니다. 사교 구조 \(\omega\)를 갖는 다양체 \(M\)을 사교 다양체 \((M,\omega)\)라고 정의하며, 항상 짝수 차원을 갖습니다.10 요약하자면, 사교 다양체 \((M,\omega)\)는 해밀턴 방정식이 정의되는 구조를 갖는 공간이나 (그래서 고전 역학을 연구할 수 있으며), 2차원 곡면들의 면적을 재는 도구를 갖고 있는 공간으로 이해할 수 있습니다.
사교 다양체의 기초 탐사: 대역성
외딴섬과 같은 새로운 공간을 처음 맞닿게 되면, 섬을 둘러보며 여러 “국소적인”(주어진 한 곳에서 충분히 작은 근방의) 부분들의 특징과 형태를 관찰해 갈 것입니다. 집을 짓기 좋아 보이는 구역, 먹을 식량을 구할 수 있는 구역과 같은 “여러 종류”의 공간들을 발견하게 됩니다. 사교 다양체라는 공간에서는 이와 같은 예상을 완전히 깨트려 버립니다.
다부Darboux 정리
모든 사교 다양체는 국소적으로 항상 똑같이 생겼습니다. 즉, 주어진 사교 다양체 \((M,\omega)\)의 임의의 점에서 아주 작은 근방을 들여다보면, 언제나 표준 사교 다양체 \((\mathbb{R}^{2n},\omega_0)\)의 작은 영역처럼 보입니다. 사교 다양체라는 섬에 불시착하여 주변을 구경하면 언제나 똑같은 모습이 보이는 괴상한 공간임을 알아차리게 됩니다. 이는 국소적인 모양이 곡률의 정보로 변화하는 리만 다양체와는 정 반대의 특징입니다. 이렇기 때문에 사교 섬에서 살아남기 위해서는 대역적인 물체object들을 관찰하여 사교적인 성질들symplectic properties을 밝혀내야 합니다.
라그랑지안 부분 다양체와 사교적 성질
리만 다양체(즉, 각도를 재는 도구가 주어진 다양체)의 경우에는
어떠한 부분 다양체11에서도 각도가 잘 측정되지만, 사교 다양체에서는 같은 일이 일어나지 않습니다. 사교 다양체 \((M,\omega)\)의 부분 다양체에서 면적을 재는 사교 구조 \(\omega\)가 항상 0의 면적을 재는 고장난 상태가 될 수 있는데, 이러한 부분 다양체 중에서 가장 큰 차원을 갖는 경우를 라그랑지안 부분 다양체Lagrangian submanifold라고 합니다. 이때, 사교 다양체가 \(2n\) 차원이라면 라그랑지안12은 그 절반인 \(n\)차원을 갖습니다. 라그랑지안의 중요성을 일찍이 인지한 와인슈타인Weinstein은 1981년에 다음과 같은 신조를 남겼습니다.[3]
사교 신조Symplectic creed
Everything is a Lagrangian submanifold.
풀어서 설명하면, 사교 다양체의 모든 사교적 대상과 성질들은 라그랑지안을 통해 표현된다는 다소 과감한 주장입니다. 한번 예를 들어보겠습니다. 해밀토니안 흐름이 주어진 역학계에서 자연스럽게 관심을 가지는 대상은 주기 궤도periodic orbit입니다. 즉, 흐름을 따라 한 바퀴 돌아오는 닫힌 곡선의 존재성과 개수는 해밀턴 역학계를 이해하는 기본적인 정보로 간주되고, 아놀드Arnold의 추측과 같은 중요한 문제와 관련이 있습니다. 이러한 주기 궤도들은 두 개의 라그랑지안들의 교점들intersections의 정보로 환원이 되기 때문에, 라그랑지안 교점이라는 기하학적 연구로 역학적인 대상인 주기 궤도 문제를 공략할 수 있습니다. 이것을 라그랑지안 플로어 호몰로지Lagrangian Floer homology[4]의 시작점으로 이해할 수 있습니다.
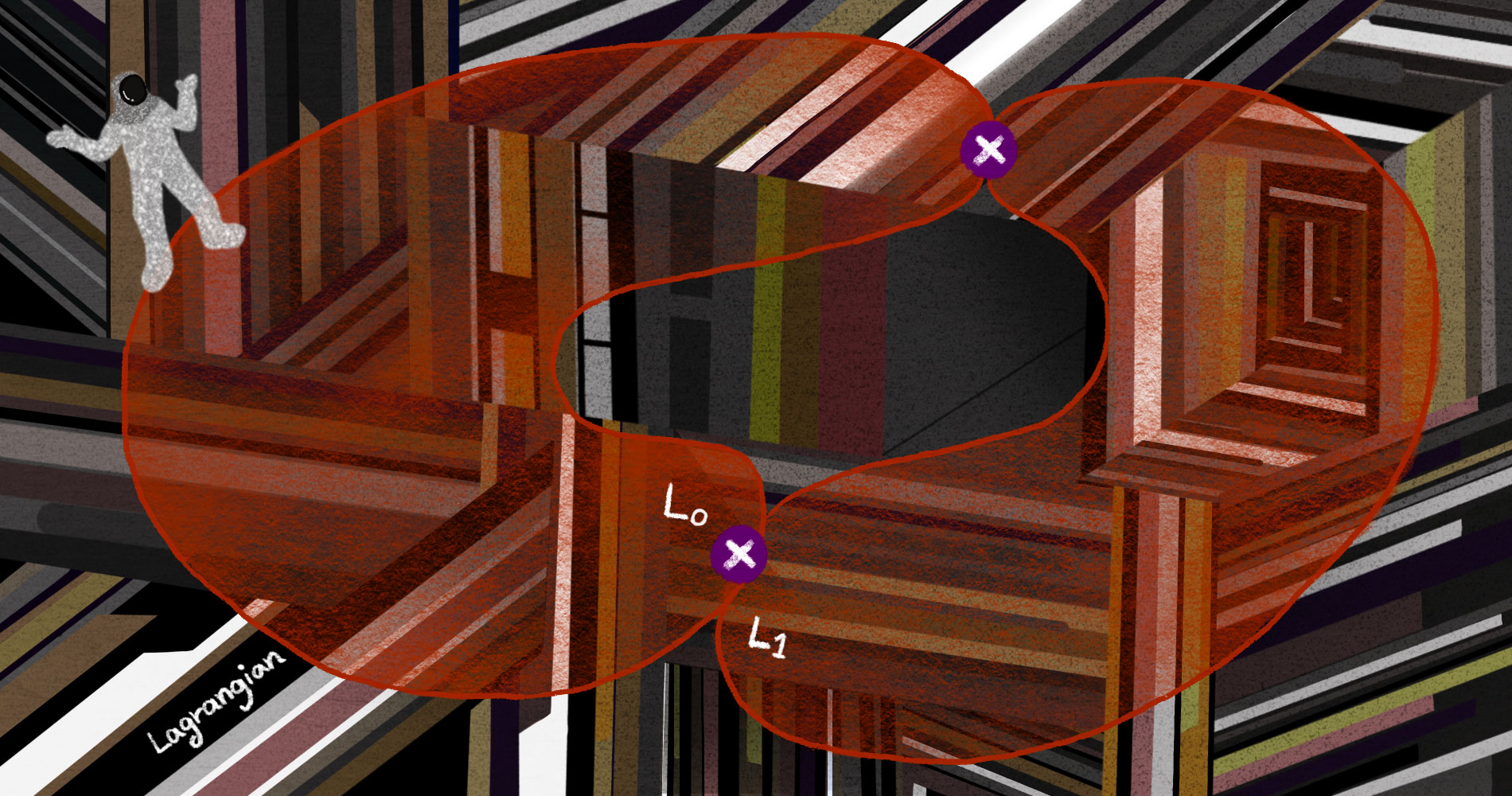
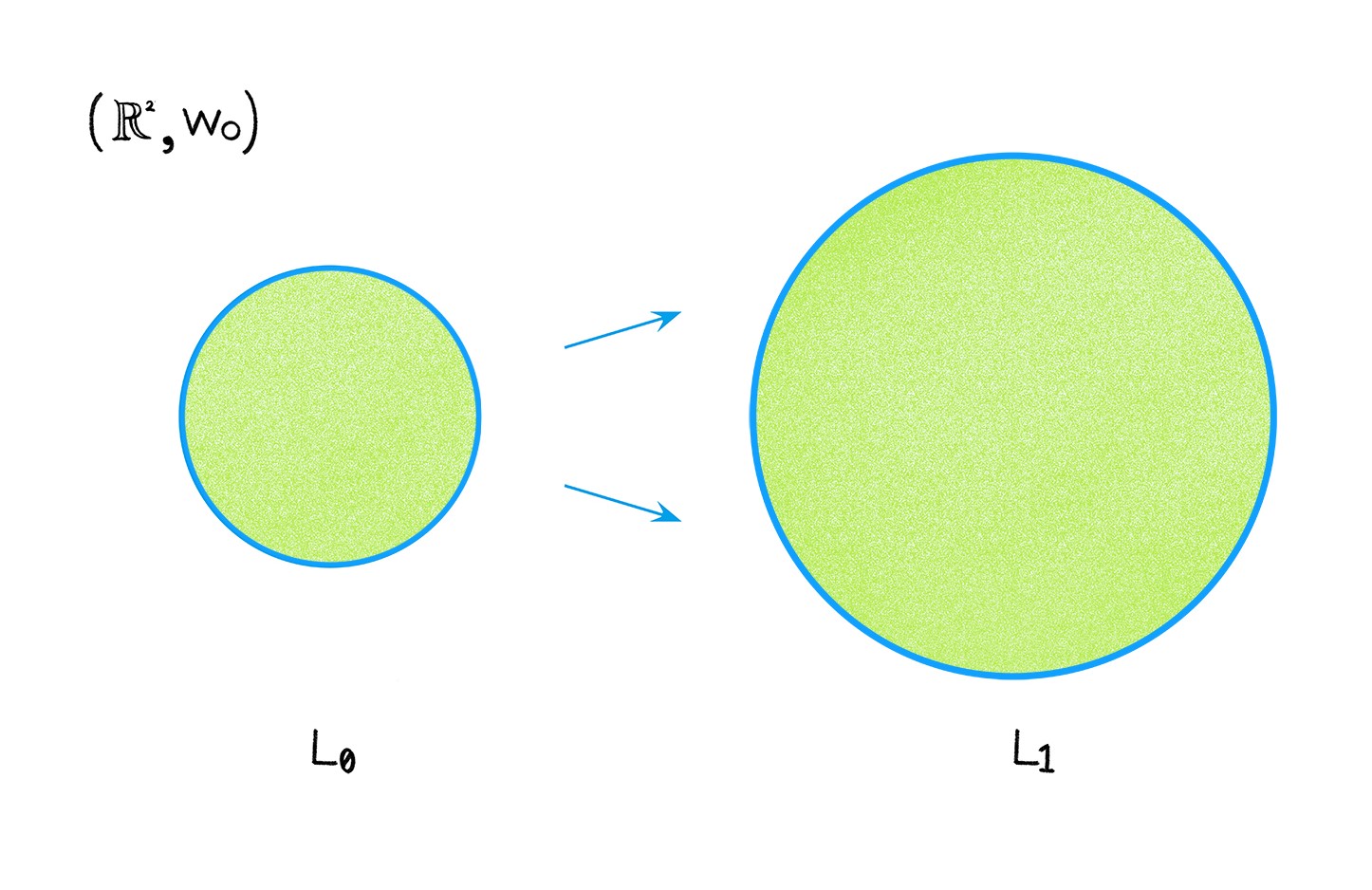
위상적인 측면에서 라그랑지안의 역할은 더욱 분명하게 다가옵니다. 2차원 평면 \(\mathbb{R}^2\)에서 반지름이 서로 다른 두 개의 원들 \(L_0,L_1\)을 생각해봅시다.[그림6]
그것들은 부드러운 변형을 통해 서로 연결되는 것을 쉽게 확인할 수 있습니다. 즉, 사교 구조를 잃은 상태에서 두 원들은 같게 볼 수 있으나, 사교적인 관점에서 두 대상은 엄연히 서로 다릅니다. 사교 기하학에서는 어떠한 해밀토니안 흐름을 통해 \(L_0\)를 \(L_1\)으로 옮길 수 있을 때, “같다(Hamiltonian isotopic)“고 생각합니다.13
푸엥카레의 정리에 따라 해밀토니안 흐름은 면적을 보존해야 하나, \(L_0\)와 \(L_1\)이 품는 원판들의 면적들이 서로 다르므로 역학적인 방법으로 \(L_0\)를 \(L_1\)으로 이동시킬 수 없습니다. 간단한 2차원 사교 다양체에서 원으로 주어지는 라그랑지안들을 통해 “작은” 사교 현상을 느껴볼 수 있지만, 면적에 관한 논의로 쉽게 해결되는 탓에 진정한genuine 사교 현상으로 간주되기는 어렵습니다. 이로서 4차원 이상의 사교 다양체에서 라그랑지안들의 위상적 특성을 분석함으로써 사교적인 현상을 인지할 수 있다는 힌트를 얻게 됩니다.
사교 다양체의 강직성과 그로모프의 유사정칙 곡선 이론
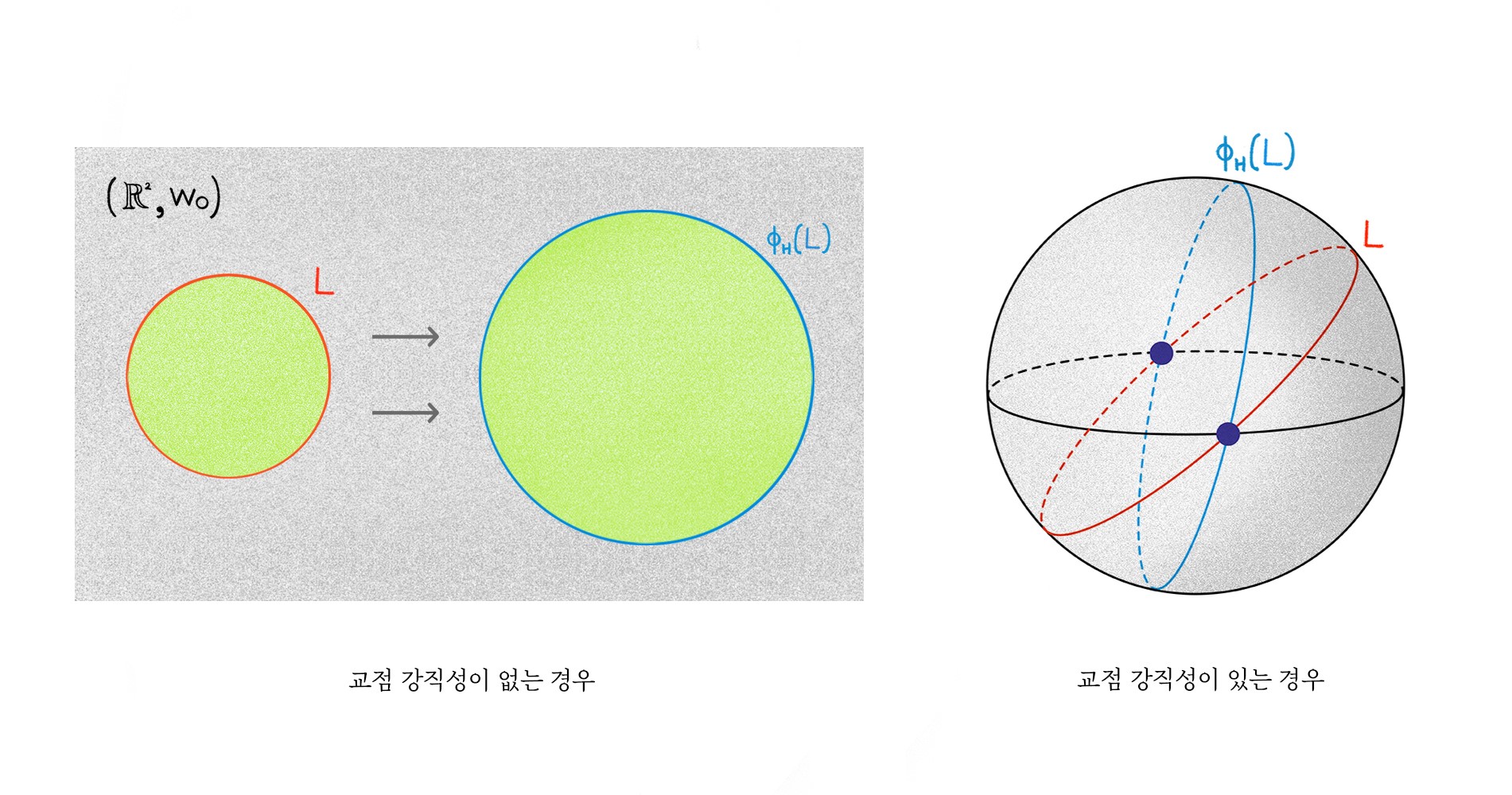
사교 다양체 \((M,\omega)\)에 주어진 라그랑지안 \(L\)이 모든 해밀토니안 흐름 \(\phi_H\colon M\to M\)에 대하여 \(\phi_H(L)\cap L\ne \emptyset\)를 만족하는 경우, \(L\)이 교점 강직성intersection rigidity을 갖는다고 말합니다.[그림7]
즉, 라그랑지안 \(L\)이 어떠한 역학적인 이동을 통해서도 자기 자신을
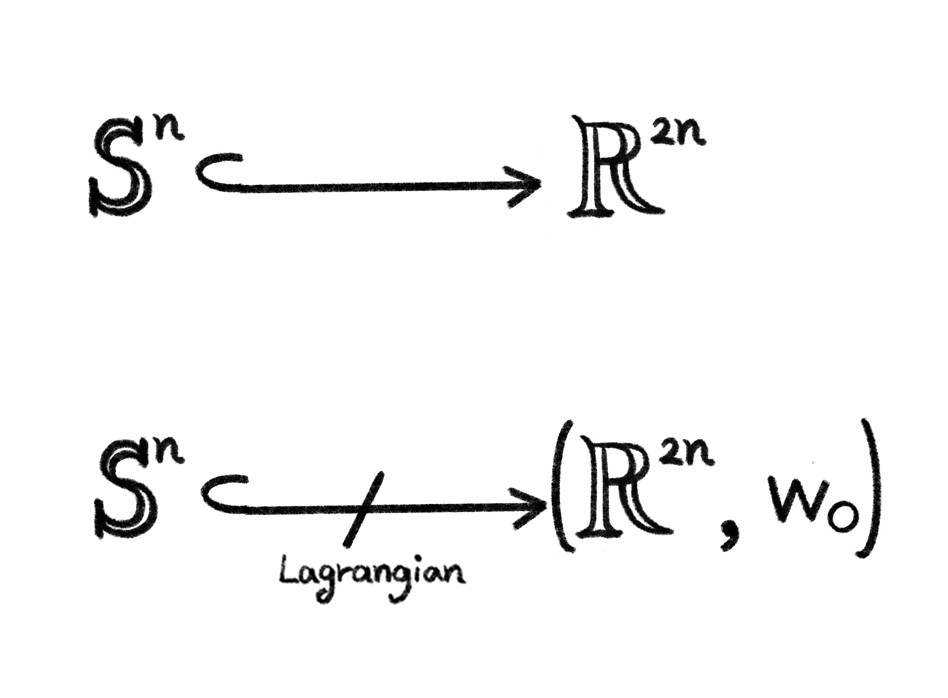
벗어날 수 없는 경우입니다. 특히, \(L\)이 라그랑지안 토러스14인 경우에는 (면적이나 부피의 보존을 무시하고) 부드러운 변형으로 \(L\)이 자기 자신을 만나지 않게 옮겨질 수 있으므로, 교점 강직성은 진정한 사교 현상으로 볼 수 있습니다.15 또 다른 강직성을 탐구하는 방법으로 라그랑지안 매장 문제Lagrangian embedding problem를 생각해볼 수 있습니다. 주어진 다양체 \(L\)을 사교 다양체 \((M,\omega)\) 속으로 라그랑지안이 되도록 넣을 수 있는지 물어보는 문제로서, \((\mathbb{R}^4,\omega_0)\)에서 라그랑지안 2차원 구 \(S^2\)16가 존재하지 않는 흥미로운 사실을 이 문제의 시작점으로 볼 수 있습니다.17 이 현상은 라그랑지안 구의 근방이 갖는 “위상적” 성질을 통해 보여지며, 이 성질이 고차원에서 일반적으로 성립하지 않아 고차원에서의 연구가 묘연했었습니다. 저차원과 마찬가지로 고차원 구 \(S^n\)도 \((\mathbb{R}^{2n},\omega_0)\)에 라그랑지안이 되도록 넣을 수 없다는 것은 그로모프Gromov에 의해 1985년에 알려졌습니다. 라그랑지안의 조건을 고려하지 않으면, \(S^n\)는 언제나 \(\mathbb{R}^{2n}\)에 넣을 수 있기 때문에, 앞선 그로모프의 결과는 사교적인 현상으로 간주하기에 손색이 없습니다.[그림8]18
사실, 그로모프가 1985년에 보인 결과[5]는 영명이 높은 그의 유사정칙 곡선 이론pseudoholomorphic curves theory의 발명inventions과 함께 파생된 수 많은 강직성 현상들 중에 하나였습니다. 이 발명을 통해 사실상 사교 위상수학이 탄생했다고 말하는 것은 과언이 아닐 것입니다.
참고문헌
- McDuff, Dusa; Salamon. Dietmar Introduction to symplectic topology. Third edition. Oxford Graduate Texts in Mathematics. Oxford University Press, Oxford, 2017. xi+623 pp. ISBN: 978-0-19-879490-5; 978-0-19-879489-9.
- Schlenk, Felix Symplectic embedding problems, old and new. Bull. Amer. Math. Soc. (N.S.) 55 (2018), no. 2, 139–182.
- Weinstein, Alan. Symplectic geometry. Bull. Amer. Math. Soc. (N.S.) 5 (1981), no. 1, 1–13.
- Floer, Andreas. Morse theory for Lagrangian intersections. J. Differential Geom. 28 (1988), no. 3, 513–547.
- Gromov, M. Pseudo holomorphic curves in symplectic manifolds. Invent. Math. 82 (1985), no. 2, 307–347.