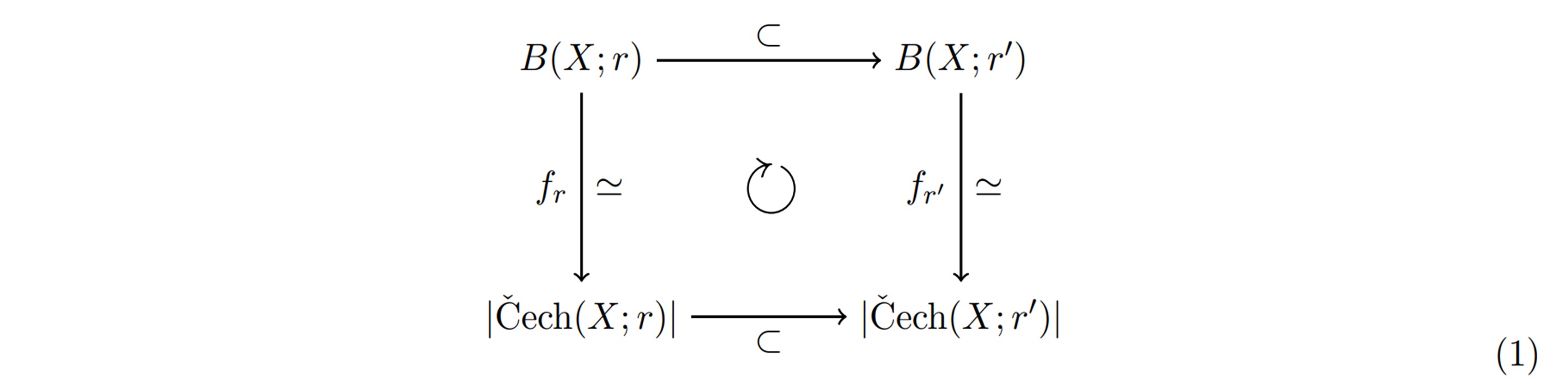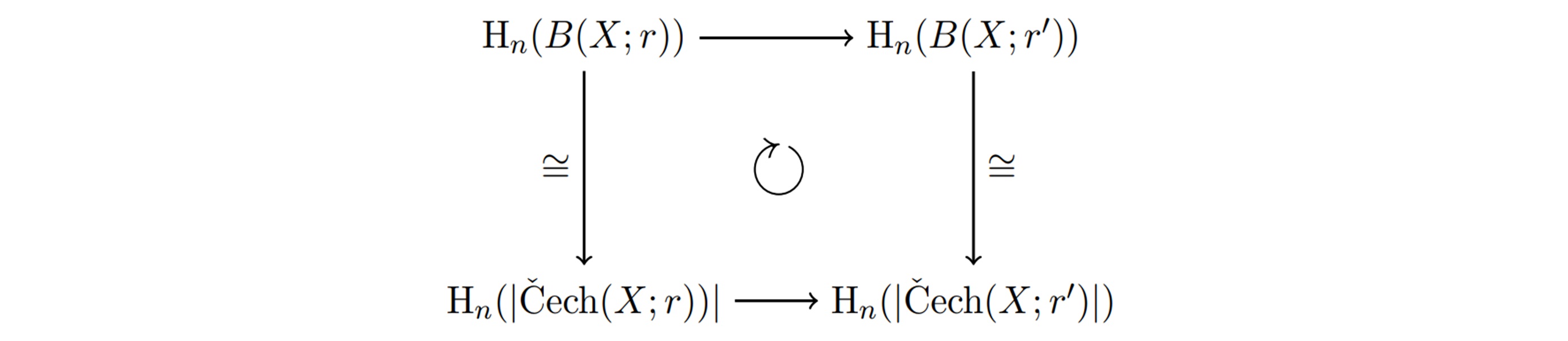들어가며
위상수학적 데이터 분석 topological data analysis(TDA) 연구 커뮤니티가 2000년대 초반 형성되기 시작한 뒤, 위상수학이 데이터 분석에서 점점 더 널리 이용되고 있다. TDA는 위상수학을 데이터 분석에서 이용하기 위한 수학적, 통계학적, 알고리즘적 기반을 다지고 이를 실제 활용하는 방법을 연구하는 분야이다. TDA의 가장 대표적인 개념 중 하나가 지속적 호몰로지 Persistent Homology이다. 지속적 호몰로지는 대수적 위상수학의 대표적인 개념인 호몰로지를 데이터 분석에 적합하도록 개량한 현대적 개념이라 할 수 있다. 이 글에서는 지속적 호몰로지의 아이디어를 소개하고자 한다.
이산적인 데이터의 모양을 어떻게 측량할까?
지속적 호몰로지는 어떤 기하적/위상적 정보를 가진 혹은 가졌다고 믿는 유클리드 공간 속 유한개의 점으로 구성된 데이터를 분석할 때 특히 유용하다. 유클리드 공간 속 유한개의 점으로 구성된 집합을 점구름 point cloud 이라 부르자. 예를들어 어떤 물질의 원자 배열구조가 주어졌을 때 원자의 중심들은 3차원 공간 안의 점구름이 된다 (그림 1). 또한, 많은 응용사례에서 어떤 다양체 manifold 또는 의사다양체 pseudomanifold에서 점구름이 실제 추출되거나, 그렇다고 가정된다. 이러한 경우 점구름의 모양은 그 출처 공간에 대한 중요한 기하적/위상적 정보를 담는 것이 분명하다.
예를들어, 점구름으로 주어진 데이터 \(X\)가 그림 2와 같이 평면 위에 주어졌다고 하자. 이 데이터는 숫자 8에서 몇 개의 점을 추출한 것과 같이 보인다. 우리는 이 점구름으로부터 연속적인 형체 8을 떠올리는게 자연스러운데, 이러한 추론을 컴퓨터도 스스로 할 수 있을까?
우리가 숫자 8을 떠올린 이유를 생각해보자. 아마도 가까운 점들끼리는 연결되어 있다고 상상했기 때문일 것이다. 이를 좀 더 정밀한 방법으로 기술해보자. 주어진 점구름 \(X\)를 ‘대충보는 정도’ 를 나타내는 어떤 ‘적당한’ 양의 실수 \(r\)를 정하자. 여기서 \(r\)만큼 대충본다는 것은 각 점 \(x\in X\) 대신 \(x\)를 중심으로 하는 반지름 \(r\)인 원반 disk으로 대체하여 바라보겠다는 것이다 (그림 3).
이 원반들의 합을 \(B(X;r)\)로 표기하자. 적당한 \(r\) 의 선택 덕분에 \(B(X;r)\)은 뚜렷이 8의 형태를 갖는다. 엄밀히 말해 숫자 8과 \(B(X;r)\)은 호모토피 동치 homotopy equivalent인데, 이는 \(B(X;r)\)을 고무찰흙으로 만들어진 물체라 상상한 뒤 ’연속적인 변형’을 통해 구부리거나, 늘리거나, 압축하는 등 숫자 8로 만들 수 있다는 의미로 생각하면 무리가 없다. 물론 8의 형태를 갖게된 결정적인 이유는 원반들의 반지름 \(r\)을 적당히 잘 잡았기 때문이다. \(r\)이 충분히 작았다면 \(B(X;r)\)은 기존의 점구름 형태와 별반 다르지 않을 것이고 \(r\) 이 충분히 크다면 \(B(X;r)\)은 하나의 커다란 덩어리 형태일 것이다. 그런데 사실 임의의 점구름이 주어졌을 때 각 점을 대체할 원반의 적당한 반지름 \(r\)이라는 것은 정의된 바가 없음에 주목하자. 게다가 딱히 잘 정의할 방법도 떠오르지 않는다!
그렇다면 적당한 \(r\)을 고르는 대신 모든 실수 \(r\geq 0\)을 고려하기로 하면 어떨까? \(r\)이 0부터 증가함에 \(B(X;r)\)은 점점 더 커져 그림 4가 묘사하듯
(1) 처음에는 서로 겹치지 않는 원반들의 형태를 띄다가
(2) 두 구멍이 형성되어 8의 형태를 갖고 즉, 크기가 다른 두 구멍이 생성됨
(3) 작은 구멍이 먼저 메워지며 사라지고
(4) 나중에는 큰 구멍 역시 메워져 사라진다.
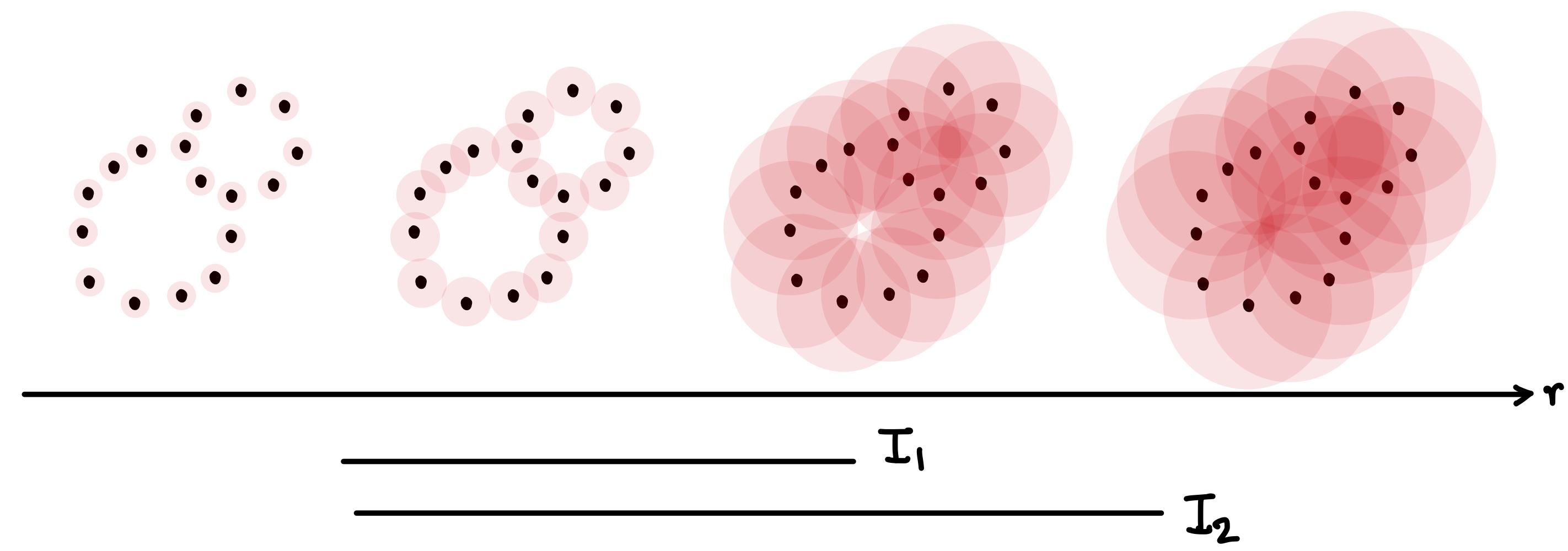
그림 4와 같이 구간 \(I_1\), \(I_2\)를 각각 작은 구멍, 큰 구멍이 ‘살아있는’ \(r\)의 값들의 모임으로 정의할 수 있다. 이 두 구간을 어떻게 정확히 계산할 수 있는지 살펴보기 위하여 호몰로지에 대해 조금 더 자세히 살펴볼 것이다. 예시로 주어진 점구름은 아주 단순해서 두 구간 \(I_1\), \(I_2\)를 더 엄밀하게 정의하고 계산할 필요성에 대해 느끼지 못할 수 있다. 그러나 만약 점구름 \(X\)가 4차원의 유클리드 공간안에 있고 2차원 원반대신 4차원 원반들의 합 \(B(X;r)\)을 고려하면, 우리는 \(X\)나 \(B(X;r)\)을 눈으로 직접 볼 수 없기 때문에 위와 같이 시각화에 의존하는 방식은 통하지 않는다. 또한 저차원 공간에 주어진 점구름이라 할지라도 점의 개수가 많아지고 그 형태가 조금만 복잡해지면 구멍들을 인지하고 각 구멍에 이름을 붙이는 것 자체가 쉽지 않은 작업이다.
구멍과 그를 위한 대수학–호몰로지
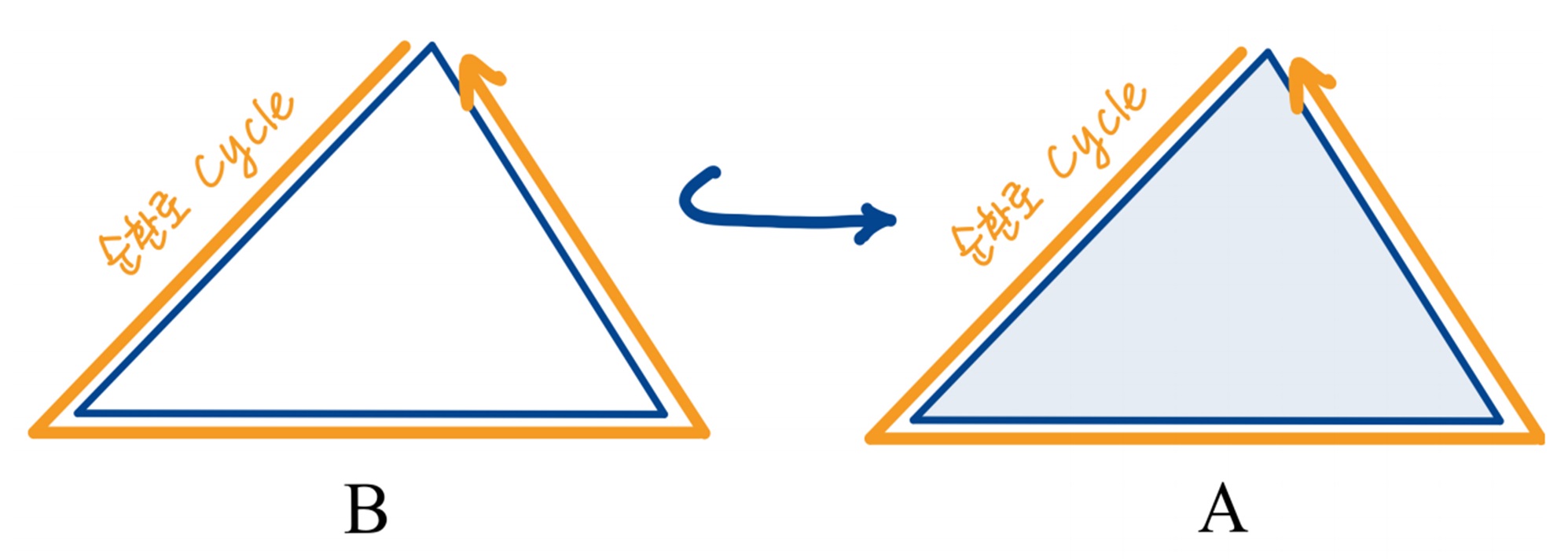
백형렬 교수님이 예전에 기고한 Horizon의 기사 ‘거리 개념이 없는 세상에서 가깝고 멂을 정의하기‘에서 ‘형태가 주어진 집합’을 위상공간이라 부르기로 했다는 것을 기억해보자. 우리가 지금 살펴볼 호몰로지는 위상공간 안에 ’구멍’의 존재와 그 ’구멍’들 사이의 연결관계에 대해서 서술하는 대수적인 도구이다. 그런데 ‘구멍’이란 것이 무엇일까? 가령 속이 찬 삼각형 A와 속이 빈 삼각형 B가 있다고 하자 (그림 5).

직관적으로 볼 때, A에는 구멍이 없고 B에는 구멍이 있다. 왜 그러하다고 생각했을까? 먼저 A와 B 모두 세 변을 따라서 한 바퀴 도는 순환로 cycle가 있다. 그런데 A의 순환로는 ‘A 내부영역’ 색칠된 부분의 경계 boundary인 반면에 B의 순환로는 ‘B 내부영역’의 경계가 아니다 ‘B 내부영역’은 없음을 기억하자. 즉, ‘순환로이면서 내부영역의 경계는 아닌 것’ 이 구멍에 대한 개념의 본질이라 할 수 있겠다. 특히 이 예시에서 순환로가 1차원적이므로 B의 구멍은 1차원 구멍이라 하겠다. 한 차원 높은 예시로 꽉찬 정사면체와 속이 빈 정사면체 네 면은 포함됨을 생각해보자. (그림 6). 전자는 어떠한 구멍도 갖지 않는 반면 후자는 ‘속이 비었다’는 사실이 2차원 구멍을 가졌음을 의미한다. 여기서 2차원 순환로는 정사면체의 네 개의 면으로 구성된다.

대수적 위상수학에서는 어떤 주어진 위상공간 \(X\)의 순환로와 경계를 엄밀하게 정의한다. 순환로들의 집합과 경계들의 집합에는 더하기와 빼기를 정의할 수 있어서 군 group을 이룬다. 백형렬 교수님의 또다른 Horizon 기사 ‘자유를 원한다면 탁구를 쳐라‘ 에서 군의 뜻을 찾아볼 수 있다. 특히 경계는 늘 순환로이며, 이 때문에 경계 군 boundary group은 순환로 군 cycle group에 포함된다. 경계군으로 순환로 군을 나눈 것quotient을 호몰로지 군 homology group이라고 부른다. 요컨대, 순환로이면서 내부영역의 경계는 아닌 것 즉, 구멍을 대수학적 방식으로 서술한 것이 바로 호몰로지 군이다. 위의 예시에서 봤듯이 순환로와 경계에는 차원을 부여할 수 있는데, \(n\)차원 순환로 군을 \(n\)차원 경계 군으로 나눈 군을 \(n\)차원 호몰로지 군이라고 부른다.
특히 호몰로지 군의 계수 coefficient를 체 field로 정하면 호몰로지 군은 벡터공간이 되며, 그 벡터공간의 차원을 주어진 위상공간 \(X\)의 구멍의 개수로 볼 수 있다. 사실 어떤 체를 계수로 쓰냐에 따라 벡터공간의 차원이 달라질 수 있는데, 이에 대한 자세한 논의는 생략한다. 임의의 체 \(\mathbb{F}\)를 고정하고 앞으론 이를 호몰로지 군의 계수로 쓴다고 하자. 예를 들어,
그림 5, A에 대하여. 모든 차원의 호몰로지 군은 \(0\)이다. 즉, 모든 차원의 구멍이 없다. 이를 수식으로 다음과 같이 쓸 수 있다: 모든 정수 \(n\geq0\)에 대하여
\(H_n(A;\mathbb{F})=0.\)
그림 5, B에 대해서 1차원 호몰로지 군은 벡터공간 F와 동형이다. 그 외 차원의 호몰로지 군은 0이다. 즉, 1차원 구멍이 하나 존재하고 나머지 차원의 구멍은 없다.
\[H_n(B;\mathbb{F})=\begin{cases}\mathbb{F},&n=1\\0,&n=0,2,3,\ldots.\end{cases}\]
연속함수는 구멍을 보존할까?–호몰로지의 함자성
예전에 백형렬 교수님이 기고하신 Horizon의 기사 ‘연속성의 상대성‘에서 두 위상공간 사이의 함수의 연속성, 그리고 위상구조에 따른 연속성의 상대성에 대해서 살펴보았다. 앞 절에서 이야기한 호몰로지는 두 위상공간 사이의 연속함수에 대해서도 사실 정의할 수 있다. 두 위상공간 \(A\)와 \(B\)가 주어지고 그 사이의 연속함수 \(f:A\rightarrow B\)가 주어졌다고 하자. \(A\)에 있는 구멍이 \(f\)에 의해 \(B\)로 사상될 때 그 상image이 여전히 구멍에 해당하는가는 \(f\)에 대한 중요한 정보이다. 우리가 \(n\)차원 구멍의 보존에 대해 관심이 있다면, \(f\)의 \(n\)차원 호몰로지인 \(H_n(f;\mathbb{F})\)를 계산해보면 된다. \(H_n(f;\mathbb{F})\)은 다름아닌 벡터공간 \(H_n(A;\mathbb{F})\)에서 벡터공간 \(H_n(B;\mathbb{F})\)으로 가는 선형사상이다. 이 선형사상의 랭크rank가 클수록 \(f\)의 `구멍보존성’이 높다고 할 수 있다. 특히 고무찰흙으로 만들어진 어떤 위상공간 A를 다른 위상공간 B로 연속적 변형 \(f:A\rightarrow B\) 을 통해 만들어낼 수 있다면 즉, \(f\)가 호모토피 동치라면 모든 \(n\)에 대하여 선형사상 \(H_n(f;\mathbb{F}):H_n(A;\mathbb{F})\rightarrow H_n(B;\mathbb{F})\)은 동형사상isomorphism이다. 이는 구멍보존성이 최대치인 예라 할 수 있다.
또다른 예로 \(A\)와 \(B\)가 그림 5와 같이 주어진 공간이라 하고 함수 \(i\)를 \(B\)에서 \(A\)로 가는 자연스러운 포함함수라고 하자. 즉, \(B\)를 \(A\)에 왜곡없이 고스란히 매립하는 함수를 떠올리면 된다. 이 때, \(B\)의 순환로가 \(i\)에 의해 \(A\)의 순환로로 보내진다 (그림 7).
그런데 그 순환로가 \(B\)에서 구멍이었을지언정 \(A\)에서는 구멍이 아님을 보았다. 이 사실은 \(i\)에 대응하는 1차원 호몰로지는 영함수 \(H_1(i;\mathbb{F}):\mathbb{F}\rightarrow 0\) 로서 그 랭크가 \(0\)임으로 나타난다.
점점 더 커지는 연속적 물체를 점점 더 커지는 이산적 물체로 요약하기
이제 그림 4와 같이 점점 커지는 유한개의 원반합에서 구멍의 생성과 소멸을 어떻게 컴퓨터가 계산할 수 있을지 알아보자 다시 강조하지만 시각화에 의존하는 방법은 충분치 않다. 먼저 음이 아닌 실수 \(r\)을 고정하자. 좌표평면 위의 임의의 점 \(x\)에 대하여 \(B(x;r)\) 을 \(x\)를 중심으로하는 반지름 \(r\)의 닫힌 원반이라 하자. 그러면 앞에서 정의한 원반들의 합 \(B(X;r)\)은 모든 \(x\in X\)에 대한 \(B(x;r)\)의 합집합이다. 다음 \(X\)의 부분집합들의 모임을 생각하자.
\[\\\breve{C}ech(X;r)=\left\{A\subset X:\bigcap_{x\in A}B(x;r)\neq\emptyset\right\}.\]
이 집합은 \(X\)의 \(r\)-체흐 복합체라 불린다. 위 수식을 찬찬히 해석해보면 다음을 알아낼 수 있다.
1. 모든 점 \(x\in X\)에 대해 \(\{x\}\in \breve{C}ech(X;r)\).
2. 임의의 두 점 \(x_1,x_2\in X\)에 대하여 두 원반 \(B(x_1;r)\)과 \(B(x_2;r)\)가 겹치면 \(\{x_1,x_2\}\in \breve{C}ech(X;r)\).
\[\vdots\]
n. \(X\)에 포함된 임의의 서로 다른 \(n\)개 점에 대해 그들이 대응하는 원반들의 교집합이 비어있지 않으면 그 \(n\)개 점으로 구성된 집합은 \(\breve{C}ech(X;r)\)의 원소이다.
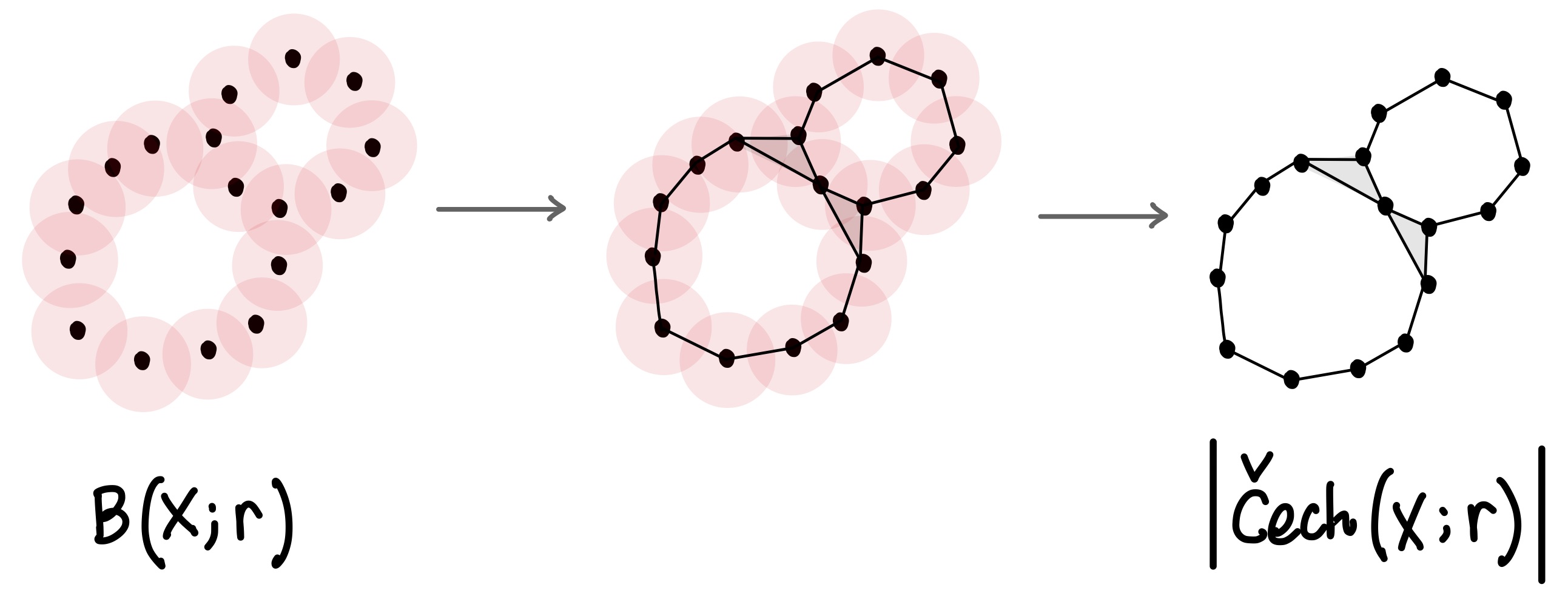
위에서 보듯이 \(\breve{C}ech(X;r)\)는 유한집합 \(X\)의 특정 부분집합들로 구성된 모임일 뿐이므로, 어떤 무한개의 점을 포함하는 연속적인 위상공간과는 다르다. 그럼에도 불구하고 \(\breve{C}ech(X;r)\)로부터 다음과 같은 연속적인 위상공간을 떠올릴 수 있다: 임의의 \(A\in \breve{C}ech(X;r)\)의 원소의 개수가 1개이면 점, 2개이면 선분, 3개이면 속이 찬 삼각형, 4개이면 속이 찬 정사면체 등등, \(n\)개이면 \(n\)개의 점으로부터 생성되는 \(n-1\)차원의 볼록껍질convex hull 으로 치환하여 생각한다. 이들의 합으로 구성된 연속적인 공간을 \(\breve{C}ech(X;r)\)의 기하적 실체}라 하고 \(|\breve{C}ech(X;r)|\)라 쓴다 (그림 8).
Figure 8:
다음 두 가지에 주목하자.
(1) 그림 8에서 \(B(X;r)\) 형태로 주어진 고무찰흙은 연속적 변형을 통해 \(|\breve{C}ech(X;r)|\) 형태의 고무찰흙으로 만드는 게 가능하다는 것을 관찰하자. 이는 이 예시에서만이 아니라 일반적으로 참이다. 즉, 임의의 점구름 \(X\)와 임의의 실수 \(r\geq 0\)에 대하여 \(B(X;r)\)은 \(|\breve{C}ech(X;r)|\)와 호모토피 동치이다. 이를 \(B(X;r)\simeq|\breve{C}ech(X;r)|\)로 쓰자. 신경정리Nerve theorem가 이를 함의한다.
(2) 임의의 실수쌍 \(0\leq r\leq r’\) 에 대하여 포함관계 \(B(X;r)\subset B(X;r’)\)와 \(\breve{C}ech(X;r)\subset \breve{C}ech(X;r’)\)가 성립한다. 두 번째 포함관계는 \(|\breve{C}ech(X;r)|\subset |\breve{C}ech(X;r’)|\)를 함의한다.
(1)에서 언급된 각 \(r\)에서의 연속적 변형은 (2)에서의 포함관계들과 잘 조화되도록 선택할 수 있다. 이말인즉슨, 매개변수 \(r\)로 색인된 연속적 변형들의 모임 \(\{f_r:B(X;r)\rightarrow |\breve{C}ech(X;r)|\}_{r\geq 0}\) 이 존재하여 모든 실수쌍 \(0\leq r\leq r’\) 에 대하여
(a) \(B(X;r)\) 에서 \(|\breve{C}ech(X;r)|\) 로의 연속적 변형 \(f_r\)를 가한 뒤에 \(|\breve{C}ech(X;r)|\)를 \(|\breve{C}ech(X;r’)|\) 에 매립embedding하는 것과
(b) \(B(X;r)\) 을 \(B(X;r’)\)에 먼저 매립하고 \(B(X;r’)\)를 \(|\breve{C}ech(X;r’)|\)로 연속적 변형 \(f_{r’}\)을 가하는 것
은 동일한 결과를 낳는다. 다르게 말하면 모든 실수쌍 \(0\leq r\leq r’\) 에 대하여 다음 포함함수들inclusion maps 가로 화살표들과 호모토피 동치 함수들세로 화살표들로 이루어진 다이어그램이 순환한다.
이는 함자적 신경정리에 의한 결과이다 [1].
종합하자면 \(B(X;r)\)의 위상구조에 대한 정보는 이산적 물체인 \(\breve{C}ech(X;r)\)에 요약되며 그 요약방식은 \(r\)의 변화에 대해서 일관적 혹은 자연적으로 설정될 수 있다.
우리가 예시로 이용한 숫자 8 형태의 점구름은 2차원 평면에 포함되어 있지만, 위의 정의와 정리들은 다른 차원으로도 자연스럽게 일반화된다. 예를들어 만약 점구름이 3차원 좌표공간 공간안에 주어진다면 \(B(x;r)\)를 2차원 원반 대신 3차원 원반 (속이 찬 구)으로 대체하기만 하면 위의 다이어그램 (1) 이 순환한다.
모든 실수쌍 \(0\leq r\leq r’\) 에 대하여 다이어그램 (1)이 순환한다는 것은 \(r\)이 증가함에 따라 점점 커지는 공간 \(B(X;r)\)의 지속적 호몰로지(??) 계산을 점점 커지는 이산적 물체 \(\breve{C}ech(X;r)\)로 요약할 수 있음을 의미하며, 이는 \(B(X;r)\)의 지속적 호몰로지 계산을 알고리즘으로 구현할 수 있게 해주는 중요한 징검다리 역할을 한다.
점구름의 모양을 바코드에 담아내기
호몰로지의 계수가 어떤 체 \(\mathbb{F}\)라 하고 \(H_n(-;\mathbb{F})\) 대신 \(H_n(-)\)로 간단히 쓰기로 하자. 모든 실수쌍 \(0\leq r\leq r’\) 에 대하여 다이어그램(1)이 순환한다는 사실은 곧 모든 실수쌍 \(0\leq r\leq r’\)에 대하여 다음 다이어그램이 순환한다는 것을 의미한다.
여기서 가로 화살표는 포함함수들의 호몰로지를 나타내고 세로 화살표는 호모토피 동치의 호몰로지이므로 동형함수이다 동형함수 임을 강조하고자 \(\cong\)를 썼다. 특히 위상공간 \(|\breve{C}ech(X;r)|\)는 유한집합 \(\breve{C}ech(X;r)\)에 그 위상구조에 대한 정보를 완벽히 담으므로, 매개변수화된 호몰로지 군의 모임 \(\{H_n(|\breve{C}ech(X;r)|)\}_{r\geq 0}\)에 대한 모든 대수적인 정보는 유한집합들의 매개변수화된 모임 \(\{\breve{C}ech(X;r)\}_{r\geq 0}\)으로부터 얻어질 수 있다.
그런데 \(\{H_n(|\breve{C}ech(X;r)|)\}_{r\geq 0}\) 의 대수적인 구조는 집합 \([0,\infty)\) 안의 실구간들의 집합으로 완벽하게 특성화될 수 있는데, 이는 이 글에서는 다루지 않는 어떤 대수적인 정리에 따른다 [7]. 이 실구간들의 집합을 \(X\)의 \(n\)번째 체흐 지속적 호몰로지 바코드라고 부른다. 이 바코드는 당연히 이산적인 물체인 \(\{\breve{C}ech(X;r)\}_{r\geq 0}\) 로부터 계산될 수 있다. 바코드에 있는 각 실구간은 \(r\)의 증가에 따라 원반합 \(B(X;r)\)에 나타나고 사라지는 특정 \(n\)차원 구멍에 대응한다. 그림 4에 나오는 두 구간 \(I_1\)과 \(I_2\)의 모임이 바로 그림 2에 있는 점구름 \(X\) 의 1번째 체흐 지속적 호몰로지 바코드를 나타낸다. 두 개의 다른 길이의 실구간은 크기가 다른 두 개의 구멍이 \(X\)에 존재함을 시사한다.
지속적 호몰로지가 처음 도입되던 때에는 바코드에 있는 짧은 구간들은 별로 의미 없는 정보이고 긴 구간들이 데이터에 대한 의미있고 중요한 기하/위상적 정보로 인식되었었다. 하지만 더 최근의 연구에서는 데이터가 곡면으로부터 추출될 때 그 곡면의 곡률에 대한 정보가 짧은 구간에 담겨있을 수 있음이 알려졌다 [3]. 즉, 짧은 구간도 유용한 정보를 담고 있을 수 있다.
실제로 어떻게 바코드를 컴퓨터로 계산할 수 있을까? \(X\)가 유클리드 공간 안의 점구름이었음을 기억하자. 이 경우 각 부분집합 \(A\subset X\)에 대해 \(A\)를 포함하는 가장 작은 구의 반지름을 계산하고 \(X\)위에 지어지는 체흐 복합체의 구조를 하나의 행렬로 나타낸 뒤에 기본 행/열 연산을 통해서 바코드를 계산할 수 있다. 이러한 모든 과정의 계산을 위한 소프트웨어는 이미 개발되어 있으며 프로그래밍 언어 Python이나 R에서 각각 scikit-TDA 와 TDA라는 Library를 불러와 쉽게 수행할 수 있다.
마치며
지속적 호몰로지는 점구름으로 주어진 데이터의 국소적/거시적인 연결형태를 바코드로 기술하는데에 유용한 도구임을 살펴보았다. 이는 기존의 통계학이 제공하지 않던 데이터에 대한 새로운 시각을 제시한다. 점구름 데이터로부터 지속적 호몰로지를 만드는 방법은 체흐 복합체를 이용하는 방법 외에도 여러가지가 있으며 [9], 그들에 대응하는 바코드가 있어서 주어진 데이터를 다양한 시각에서 분석할 수 있다. 또한 점구름 외에도 지속적 호몰로지를 유도할 수 있는 다양한 형태의 데이터가 있다 [5].
특정한 방식으로 지속적 호몰로지를 얻을 때 그 방법이 실제 응용에서 유용하게 쓰이기 위해서는 만들어지는 지속적 호몰로지의 바코드가 데이터의 소음으로부터 안정적인지 수학적으로 증명할 필요가 있다. 예를들어 이 글에서 본 점구름의 체흐 복합체로부터 바코드를 얻은 경우 그로모프-하우스도르프 거리 Gromov-Hausdorff distance를 에 대한 그 안정성이 증명되었다 [6]. 박지원 교수님이 쓰신 Horizon 기사 ‘휘어진 공간의 극한은 어떻게 생겼을까‘ 에서 그로모프-하우스도르프 거리가 무엇인지 찾을 수 있다.. 이렇게 바코드의 안정성을 증명하거나 지속적 호몰로지를 더 추상화하여 연구하는 데에는 위상수학 뿐만 아니라 대수학, 범주론, 조합론 등 다양한 수학이 이용된다는 것이 흥미로운 점이다 [4, 12]. 또한 지속적 호몰로지를 리만 다양체로부터 특정한 방식으로 유도하면 리만 다양체의 중요한 정보가 바코드에 담긴다는 사실이 밝혀지기도 했다 [11].
현재 지속적 호몰로지에 대하여 활발히 연구되고 있는 주제를 몇가지 소개하자면 지속적 호몰로지의 일반화 격인 다매개변수 지속적 호몰로지의 바코드를 정의하는 문제 [2, 10], 지속적 호몰로지 바코드의 통계적인 분석을 위한 이론적 토대 [14], 지속적 호몰로지 바코드의 효과적인 계산 [8], 기계학습에서 지속적 호몰로지 바코드의 활용방법 개발 등이 있다 [13].
참고문헌
[1] Ulrich Bauer, Michael Kerber, Fabian Roll, and Alexander Rolle. A unified view on the functorial nerve theorem and its variations. Expositiones Mathematicae, 2023.
[2] Magnus Bakke Botnan and Michael Lesnick. An introduction to multiparameter persis-tence. In Representations of Algebras and Related Structures, International Conference on Representations of Algebras, ICRA 2020. European Mathematical Society, 2023.
[3] Peter Bubenik, Michael Hull, Dhruv Patel, and Benjamin Whittle. Persistent homology detects curvature. Inverse Problems, 36(2):025008, 2020.
[4] Peter Bubenik and Jonathan A Scott. Categorification of persistent homology. Discrete & Computational Geometry, 51(3):600–627, 2014.
[5] Gunnar Carlsson and Mikael Vejdemo-Johansson. Topological data analysis with applications. Cambridge University Press, 2021.
[6] Fr\(\acute{e}\)d\(\acute{e}\)ric Chazal, Vin De Silva, and Steve Oudot. Persistence stability for geometric com-plexes. Geometriae Dedicata, 173(1):193–214, 2014.
[7] William Crawley-Boevey. Decomposition of pointwise finite-dimensional persistence mod-ules. Journal of Algebra and its Applications, 14(05):1550066, 2015.
[8] Tamal Krishna Dey and Yusu Wang. Computational topology for data analysis. Cambridge University Press, 2022.
[9] Herbert Edelsbrunner and John L Harer. Computational topology: an introduction. American Mathematical Society, 2010.
[10] Woojin Kim and Facundo M´emoli. Persistence over posets. Notices of the American Math-ematical Society, 70(08), 2023.
[11] Sunhyuk Lim, Facundo Memoli, and Osman Berat Okutan. Vietoris-Rips persistent homology, injective metric spaces, and the filling radius. arXiv preprint arXiv:2001.07588, 2020.
[12] Steve Y Oudot. Persistence theory: from quiver epresentations to data analysis, volume 209. American Mathematical Society, 2017.
[13] Theodore Papamarkou, Tolga Birdal, Michael Bronstein, Gunnar Carlsson, Justin Curry, Yue Gao, Mustafa Hajij, Roland Kwitt, Pietro Li`o, Paolo Di Lorenzo, et al. Position paper: Challenges and opportunities in topological deep learning. arXiv preprint arXiv:2402.08871, 2024.
[14] Larry Wasserman. Topological data analysis. Annual Review of Statistics and Its Application, 5:501–532, 2018.