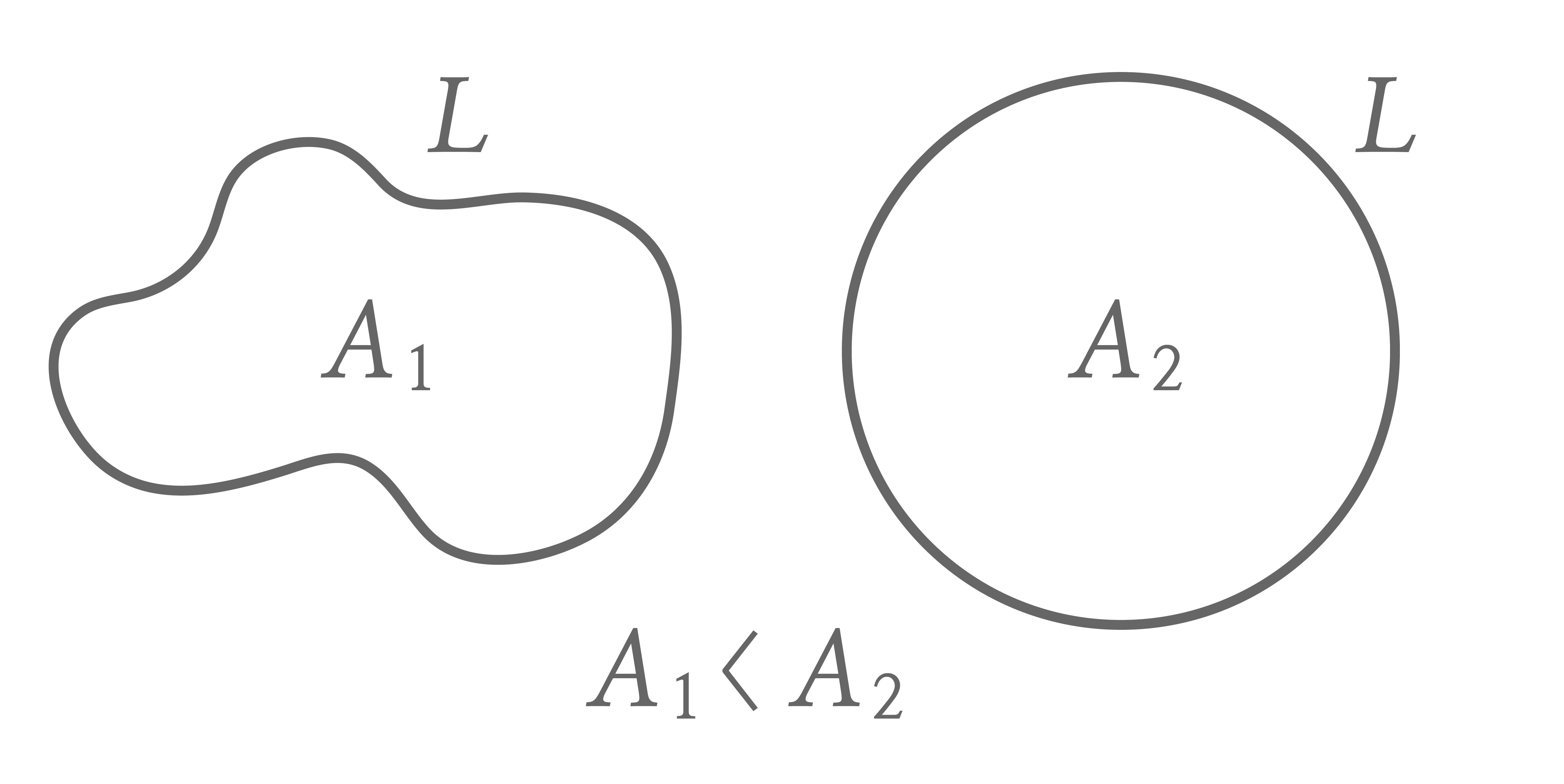기하학이 무엇인지 물었을 때 현대 수학에서 이를 몇 문장으로 정리하기는 쉽지 않습니다. 반대로 기하학에서 빠질 수 없는 것은 무엇인지를 물었을 때 길이, 면적, 모양과 같은 개념은 늘 포함 되었습니다. 등주부등식isoperimetric inequality은 이런 기하학의 기본 개념들을 이용해 기술되는 근원적인 질문 중 하나로 “평면의 주어진 길이의 곡선으로 가둘 수 있는 최대의 넓이는 얼마이고 그때의 모양은 어떤 것일까?”에 대한 답입니다. 이 답은 평면에 놓인 닫힌 곡선의 길이가 \(L\)이고 그 내부 넓이가 \(A\)라 할 때 부등식
\(4\pi A \le L^2 \)
을 항상 만족하며 등식은 곡선이 원일 때만 성립한다는 문장으로 요약됩니다. 모든 도형 중에서 원이 주어진 둘레 길이로 최대 면적을 가질 수 있다는 그럴싸한 사실은 쉽게 유추 가능해 보이며 실제 수천 년 전부터 알려져 있던 것으로 보이나 엄밀한 수학적 증명이 이뤄진 것은 19세기 야코프 슈타이너Jacob Steiner에 이르러서입니다. 수학의 발전이 인간의 직관과는 달리 얼마나 더디게 진행되며, 얼마나 많은 사람들이 노력이 필요한 일인지 상상해 볼 수 있는 예라 할 수 있겠습니다.
이후 이 질문은 호기심을 자극하는 일반적인 경우로 확장되어, 최근에는 이런 영역의 부피와 겉넓이의 상관관계를 통해 비유클리드 배경공간의 성질을 유도하고 일반상대성이론으로 기술되는 계system의 질량을 유도할 수도 있다는 연구결과들이 전해지고 있습니다. 이번 글을 통해서 간략하게나마 이러한 결과와 의미를 소개하는 기회를 갖고자 합니다. 전문적인 수식과 증명을 생략하고 결과를 직관적으로 전달하기 위해 글에 등장하는 수학적 대상들의 정확한 정의는 관심 있는 분들을 위해 각주에서 설명하도록 하겠습니다.
먼저 등주부등식의 직접적인 일반화는 고차원 유클리드 공간으로, 주어진 n-1차원 넓이를 갖는 닫힌 곡면 중 가장 넓은 n차원 부피를 가두는 형태는 구형이라는 결과가 알려져 있습니다. 이 문제는 다양한 종류의 증명이 있는데, 앞으로 다룰 내용과 관련해 살펴볼 증명은 펠릭스 슐츠F.Schulze가 발표한 곡률흐름curvature flow을 이용하는 방법입니다. 이를 간략하게 설명하자면 곡률 흐름이란 주어진 곡면을 곡률의 함수에 따른 속도로 변화시키면서 모양을 관찰하는 것을 말하는데 (최경수 교수의 HORIZON 연재글 “곡면의 열방정식”을 참고할 수 있습니다) 슐츠Schulze 교수는 곡면을 평균곡률의 n-2 거듭제곱의 속도로 변화시키면 부등식이 곡률흐름에 따라 개선되며 종국에는 곡면이 작은 구 모양의 점으로 수렴한다는 사실을 통해 초기 곡면의 등주부등식을 유도했습니다.
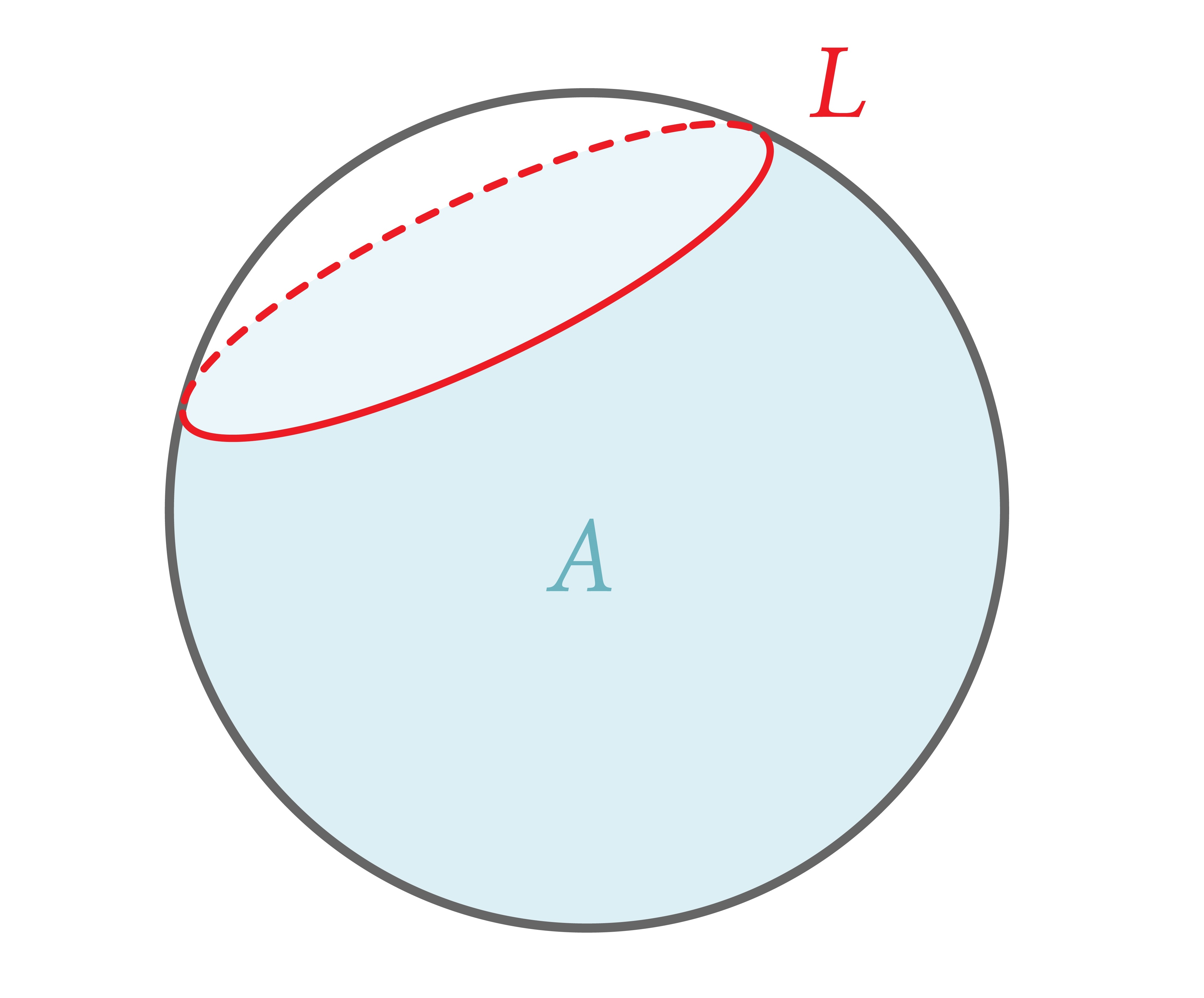
자, 그럼 이제 비유클리드 공간에서의 등주부등식을 살펴보겠습니다. 배경공간이 평면이 아니라 2차원 구인 경우를 상정해봅시다. 다시 말해 길이가 \(L\)인 시작과 끝이 이어진 실이 하나 있고 이를 2차원 구에 둘렀을 때 실로 가둘 수 있는 최대 넓이는 어떻게 될까요? 결과적으로 구의 반지름이 1일 때 곡선의 길이 \(L\)과 넓이 \(A\)의 부등식은
\( 4\pi A-A^2 \le L^2 \)
이며 등식은 곡선이 구 위의 길이 \(L\)인 원geodesic circle일 때 얻어집니다.1
곡선이 구를 면적 \(A\)와 \(4\pi-A\)의 두 개의 영역으로 나누기 때문에 부등식이 두 영역 모두에 대해 성립한다는 제법 흥미로운 사실과는 별개로, 필자가 강조하고 싶은 것은 곡선이 담을 수 있는 면적이 평면의 경우에 비해서 늘어났다는 것입니다. ‘배경공간이 어떤 양의 곡률로 휘어져 있다면 곡선으로 가둘 수 있는 면적이 유클리드 공간의 경우에 비해 늘어난다’ 여기까지만 파악하더라도 이번 글의 목적의 절반은 달성한 것이 아닌가 합니다.2
그럼 이제 질문을 반대로 바꿔보겠습니다. 어떤 휘어있는 비유클리드 공간이 배경으로 주어졌을 때, 이곳에서의 등주부등식이 유클리드 공간의 등주부등식을 얼마나 능가하는지를 측정하여 배경공간이 휘어짐을 가늠할 수 있을까요?
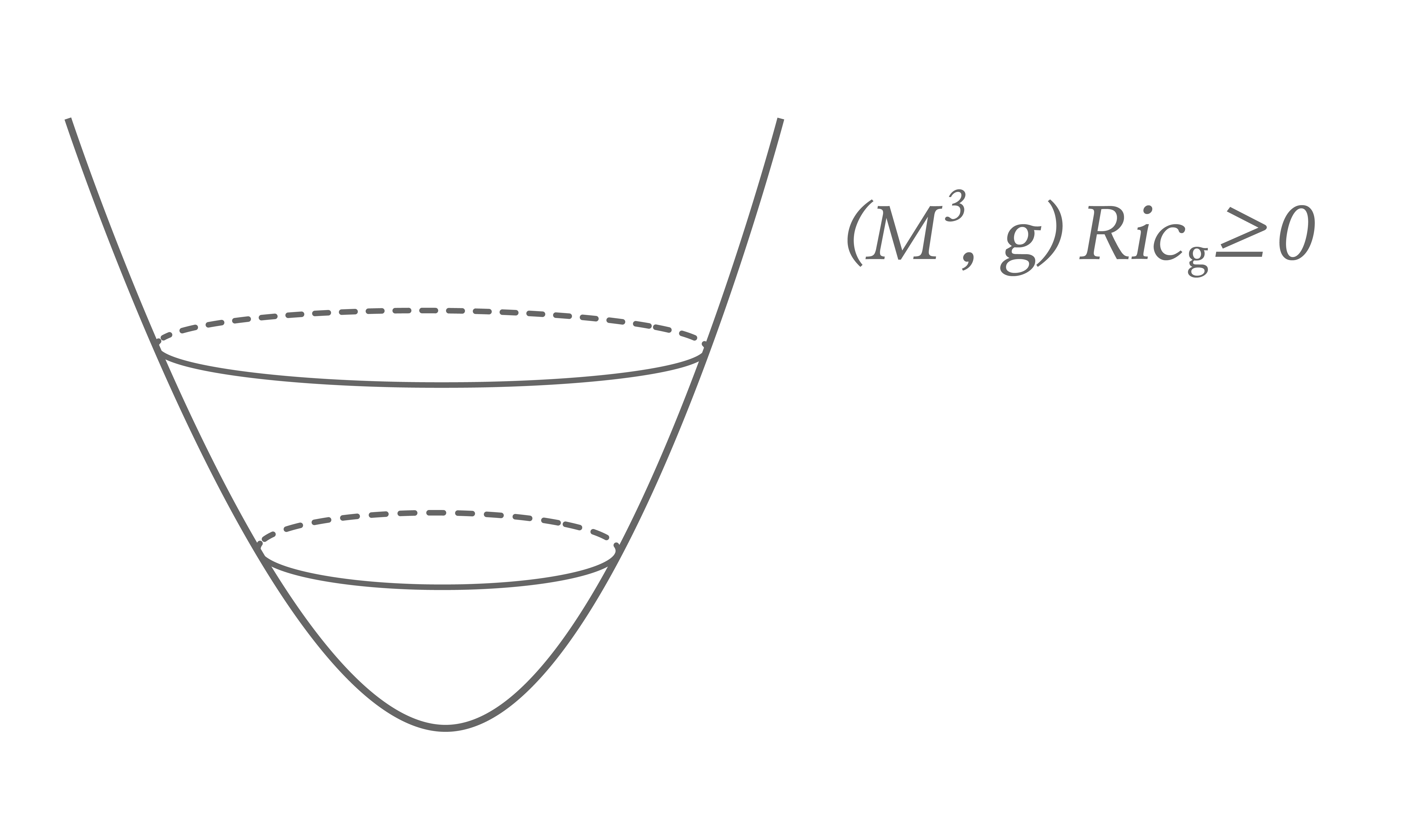
이런 방향의 결과를 하나 살펴보기 위해서 단순연결simply connected이며 리치 곡률 텐서Ricci curvature tensor가 양수인 3차원 리만다양체 \((M^3,g)\)를 생각해봅시다. (이 언어에 익숙하지 않은 독자라면 [그림3]처럼 어떤 3차원 곡면이 무한대에서 어떤 뿔cone 모양과 비슷하게 양의 곡률로 휘어져 있는 모습을 상상하면 도움이 될 것입니다.)
그리고 등주부등식의 최적상수에 대응되는 다음의 값을 생각해봅시다.3
\(C_{iso}(M^3,g):= \inf _{\Omega\subset M} \frac {A(\partial \Omega)^{3/2}}{6\pi ^{1/2} V(\Omega)}.\)
후이스켄Huisken 교수는 이 상수 \(C_{iso}\)가 다양체 안의 가능한 모든 닫힌곡면들에서 계산한 평균곡률의 적분값 중 최소값과 같다는 사실을 보였습니다.4
이쯤 되면 대부분의 독자들은 \(C_{iso}\)도, \(M\) 속 곡면들의 평균곡률 적분 중 최소값도 어떤 이유로 배경공간 \(M\)의 휘어진 정도를 나타낸다고 말하는지 의아해 하고 있으실 것입니다. 후이스켄Huisken에 의해 이 최소값과 같다고 알려진 \(C_{iso}\)는 다양체 M이 무한대에 점근적으로 비슷하게 보이는 뿔cone의 뾰족한 정도를 나타내는 뿔각cone angle을 나타냅니다.
이를 직관적으로 이해하기 위해 \((M^3,g)\)가 뿔각cone angle이 작은 무한대에서 뾰족한 다양체인 경우를 상정했을 때, 이 다양체의 먼 거리에 있는 링크부분을 \(\partial \Omega\)로 놓으면 같은 면적의 \(\partial \Omega\)로 유클리드 공간일 때보다 더 많은 부피를 포함할 수 있고 이는 \(1\)보다 작은 \(C_{iso}\)를 낳습니다.
마찬가지로 식의 우변을 살펴보아도 이런 링크에 해당하는 부분을 \(\partial \Omega\)로 생각하면 같은 사이즈의 곡면이 유클리드 공간에 있을 때보다 평균곡률이 작음을 알 수 있습니다.
(뿔의 극한에 해당하는 \(\mathbb{S}^2\times \mathbb{R}\) 실린더를 상상했을 때, \(\partial \Omega\)를 \(0\)의 곡률을 갖는 실린더의 \(\mathbb{S}^2\) 단면으로 선택할 수 있다는 사실을 떠올리면 이해하기 쉽습니다.) 이 등식의 또 다른 의미는 부피와 면적, 즉 거리의 적분으로 정의되는 양으로 정의한 \(C_{iso}\)가 곡률이라는 거리의 2계 미분을 이용해 정의한 우변의 뿔각과 같다는 사실을 통해 우변의 \(C^0\) 정칙성을 이용한 유도가 가능하다는 이야기를 담고 있기도 합니다.
이 아이디어를 확장하여 리만기하학으로 표현된 우주의 질량과 등주부등식 사이의 관계를 살펴봅시다. 먼저 아인슈타인의 일반상대성 이론에 의하면 우주의 시공간은 4차원 다양체에 로렌츠 계량Lorentzian metric이 만족하는 편미분방정식으로 요약됩니다. (오성진 교수의 HORIZON 기고글 “블랙홀 안에서는 어떤 일이 벌어질까?: 특수 상대성 이론에서 블랙홀까지”를 참고할 수 있습니다.)
이 다양체의 공간 꼴 곡면space-like hypersurface에 해당하는 3차원 다양체는 몇 가지 물리적, 수학적 가정하에서 음이 아닌 스칼라 곡률 \(R\)을 갖는 점근적 평탄 다양체asymptotically flat manifold로 기술됩니다. 여기서 어떤 3차원 다양체 \((M^3,g)\)가 점근적으로 평탄하다는 것은 주어진 계가 다른 계와 떨어져 고립되어 주변과 상호작용이 없는 상태를 모델화한 것으로 이의 수학적 정의는 무한대 위치로 다가갈수록 다양체의 리만계량Riemannian metric이 평탄한 유클리드 공간의 계량에 점근적으로 수렴하는 것을 의미합니다.5
일반상대성 이론에서는 뉴턴역학과는 다르게 단일화된 개념의 질량의 정의가 존재하지 않고 여러 종류의 정의가 혼재되어있지만 이러한 경우에 유용한 이 계의 질량의 정의는 아노윗Arnowitt, 데세르Deser, 그리고 미스너Misner에 의해 제시된 ADM 질량으로 리만계량 \(g\)의 1계 미분을 이용한 선속면적분flux integral의 무한 영역에서의 극한으로 정의됩니다.6
점근적 평탄 다양체의 질량 \(m_{ADM}\)을 구성하는 것들에는 극소곡면minimal surface으로 나타나는 블랙홀, 물질과 에너지로 인해 형성된 공간의 음이 아닌 스칼라 곡률 등이 있습니다. 블랙홀이나 공간의 양의 곡률이 질량에 기여하는데 이와 동시에 앞선 문단에서 살펴보았듯 양의 곡률은 같은 면적의 곡면에 담을 수 있는 부피를 증가시킵니다. 후이스켄Huisken 그리고 하우레기Jauregui와 Lee 교수의 연구는 이 두 개의 개념을 동치시키는 데 성공하였습니다. 이를 설명하기 위해 다양체 \(M^3\)의 영역 \(\Omega\)마다 등주부등식을 이용한 질량isoperimetric quasilocal mass을 다음과 같이 정의합시다.
\(m_{iso}(\Omega) := \frac{2}{A(\partial \Omega)} \left[ V(\Omega) – \frac{1}{6\sqrt \pi} A(\partial \Omega)^{3/2}\right] .\)
유클리드 공간의 등주부등식(각주3 참조)을 비교해 살펴보면 이 \(m_{iso}(\Omega)\)는 \(\Omega\)가 유클리드 공간의 등주부등식에 비해 얼마나 더 많은 부피를 담을 수 있는지를 나타내는 양이라는 사실을 알 수 있습니다. 결과적으로 Huisken은 \(m_{ADM}\)을 \(m_{iso}\)를 통해 다음과 같이 유도할 수 있음을 보였습니다.
\(m_{ADM} =\limsup_{A(\partial\Omega) \to \infty} m_{iso}(\Omega). \)
이 증명을 이번 글에서 다루진 않겠지만 실제 증명은 슐츠 교수가 곡률 흐름을 이용해 등주부등식을 증명한 것과 비슷한 방식으로, 평균곡률 흐름mean curvature flow과 역평균곡률 흐름inverse mean curvature flow의 단조증가 공식들을 이용하였습니다. 이 결과를 직관적으로 그리고 재미있게 비유하기 위해 후이스켄Huisken은 다음과 같은 비유를 사용했는데, 이 글을 읽는 독자들에게 가장 와닿는 설명이 아닐까 싶어 공유하며 글을 마칠까 합니다.
집 마당에 트램폴린이 있고 여러분들과 자녀가 각각 그 안에 들어가 서 있는 모습을 상상해봅시다. 여러분이 훨씬 무겁기 때문에 자녀들이 서 있을 때보다 신축성 재질의 트램폴린이 훨씬 더 길게 늘어나는 게 당연할 것입니다. 달리 말하면 같은 트램폴린의 테두리 안에 큰 질량이 들어앉으면 더 넓은 천의 면적을 확보할 수 있는 것입니다. 즉, 결과는 늘어난 천의 길이로 들어앉은 질량의 크기를 계산할 수 있다는 것을 의미합니다.
참고문헌
- Huisken, Gerhard. An isoperimetric concept for mass and quasilocal mass, Oberwolfach Reports, European Mathematical Society (EMS), Zurich 3 (2006), no. 1, 87–88.
- Huisken, Gerhard. An isoperimetric concept for the mass in general relativity, Accessed, 2015-08-31 (March 2009).
-
Jauregui, Jeffrey L., and Dan A. Lee. Lower semicontinuity of mass under \(C^0\) convergence and Huisken’s isoperimetric mass. Journal für die reine und angewandte Mathematik (Crelles Journal) 2019.756 (2019): 227-257.
-
Schulze, Felix. Nonlinear evolution by mean curvature and isoperimetric inequalities. Journal of Differential Geometry 79.2 (2008): 197-241.