우리 주변을 둘러보면 벽면을 아름답게 꾸민 타일링을 종종 볼 수 있습니다. 여기서 타일링이란 같은 모양의 도형을 이용하여 겹치지 않게 주어진 공간을 덮는 것을 의미합니다. 타일링의 다른 이름으로는 테셀레이션, 쪽매맞춤, 쪽매붙임 등이 있습니다. 이 글에서는 타일링 중에서도 특별히 반사를 이용한 타일링에 대해 알아보려고 합니다.
먼저 우리에게 가장 익숙한 공간인 평면 (좀 더 정확하게는 유클리드 평면)에서 시작해 보도록 하겠습니다. 세 개의 직선 \(\ell_1, \ell_2, \ell_3\)로 둘러싸인 삼각형 \(\Delta\)를 그려봅니다. 이 때 각각의 직선 \(\ell_i\)(\(i=1,2,3\))를 따라 반사 \(R_i\)를 생각할 수 있습니다. 즉, 평면 위에 한 점 \(x\)가 주어져 있을 때, \(R_i(x)\)는 직선 \(\ell_i\)에 대하여 \(x\)와 대칭이 되는 점입니다. 이렇게 만들어진 세 개의 반사 \(R_1, R_2, R_3\)를 이용하면 삼각형 \(\Delta\)로부터 새로운 삼각형을 얻을 수 있습니다. 예를 들어, 삼각형 \(\Delta\)에 반사 \(R_1\)을 적용하면 삼각형 \(\Delta\)와 한 변을 공유하는 삼각형 \(R_1(\Delta)\)를 얻게 됩니다. 이 때 반사 \(R_1\)을 다시 적용하면 원래의 삼각형 \(\Delta\)와 같은 삼각형이 됩니다. 하지만, 반사 \(R_1\) 대신 \(R_2\)를 적용하면 \(\Delta\)와 한 꼭짓점 \(v\)를 공유하는 삼각형 \(R_2 R_1(\Delta)\)를 얻을 수 있습니다. 삼각형 \(\Delta\)의 \(v\)에서의 각이 \(\theta\)이면, \(R_2 R_1(\Delta)\)는 \(\Delta\)를 꼭짓점 \(v\)를 중심으로 \(2\theta\)만큼 회전해서 얻어진 삼각형입니다. 따라서 각 \(\theta\)가 \(180^\circ/m\)의 형태를 가진다면 (단, \(m\)은 1보다 큰 자연수), \(\Delta\)에 \(R_1\)과 \(R_2\)를 적용하여 얻어낸 서로 다른 삼각형을 이용하여 꼭짓점 \(v\) 주변을 겹치지 않게 덮을 수 있습니다.
이 때 \(R_1\)과 \(R_2\) 뿐만 아니라 반사 \(R_3\)도 이용하면 또 다른 삼각형을 얻을 수 있습니다. 특히 삼각형 \(\Delta\)가 가지는 각이 모두 \(180^\circ/m\)의 형태를 가진다면, 삼각형 \(\Delta\)에 반사 \(R_1\), \(R_2\), \(R_3\)를 적용하여 수없이 많은 서로 다른 삼각형을 얻을 수 있을 뿐만 아니라, 이렇게 얻어진 삼각형으로 겹치지 않게 평면 전체를 덮을 수 있습니다! 또한 평면에 그릴 수 있는 삼각형이 가지는 세 각의 합이 \(180^\circ\)임을 알기에, 삼각형과 반사를 이용하여 타일링을 만들기 위해서는 세 각이 \((90^\circ,60^\circ,30^\circ)\), \((90^\circ,45^\circ,45^\circ)\) 또는 \((60^\circ,60^\circ,60^\circ)\)인 삼각형이어야 함을 알 수 있습니다. 물론 삼각형 외에도 네 각이 모두 \(90^\circ\)인 사각형의 반사를 이용하여 타일링을 만들 수 있습니다. 하지만, 모든 각이 \(180^\circ/m\) 형태를 가지는 \(n\)각형은 \(n\)이 4보다 큰 경우 평면에 존재하지 않기 때문에, 반사를 이용하여 평면의 타일링을 만들기 위한 다각형으로는 앞의 언급한 삼각형 또는 사각형 밖에 없습니다.
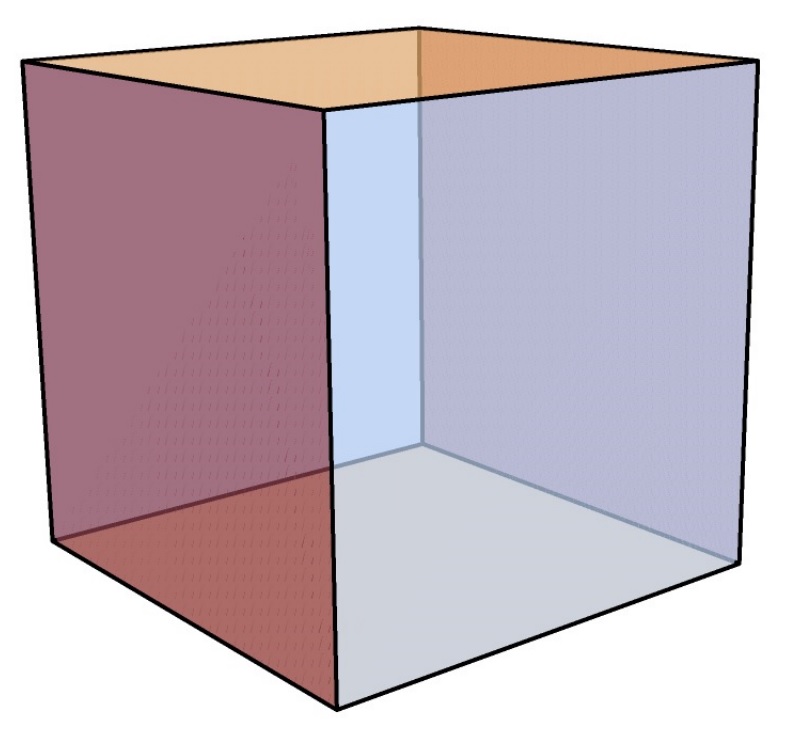
그럼, 이번에는 다음과 같은 질문을 던질 수 있습니다. ‘‘\(n\)차원 유클리드 공간에서도 유클리드 평면에서와 같이 반사를 이용하여 타일링을 만들 수 있지 않을까?’’ 여기서 \(n\)차원 유클리드 공간이란 순서를 가지는 \(n\)개의 실수의 쌍을 모아놓은 집합을 의미합니다. 유클리드 평면에서의 다각형을 대신하여, \(n\)차원 공간에서는 \((n-1)\)차원 평면으로 둘러싸인 \(n\)차원 다면체를 그릴 수 있습니다. 그리고, 각각의 \((n-1)\)차원 평면을 따라 반사를 생각합니다. 다각형에서는 두 개의 변이 꼭짓점에서 만날 때 두 변이 이루는 각이 있다면, 다면체에서는 두 개의 \((n-1)\)차원 면이 만나서 \((n-2)\)차원 면을 이룰 때 그 사이의 이면각이 있습니다. 예를 들어, \(3\)차원 사면체는 총 여섯 개의 이면각을 가지게 됩니다. 이 때 다면체의 이면각이 모두 \(180^\circ/m\)의 형태를 가진다면, 유클리드 평면에서와 같이 다면체로부터 얻은 반사를 이용하여 \(n\)차원 유클리드 공간의 타일링을 얻을 수 있습니다. 그럼, 과연 이러한 유클리드 \(n\)차원 다면체에는 어떤 것이 있을까요? 이에 대한 답을 하신 분이 콕세터Harold Scott MacDonald Coxeter 교수님이십니다 [1]. 따라서 이면각이 모두 \(180^\circ/m\)의 형태를 가지는 \(n\)차원 다면체를 우리는 콕세터 \(n\)-다면체라고 부릅니다. 예를 들어 \(3\)차원 유클리드 공간의 정육면체는 유클리드 콕세터 \(3\)-다면체입니다.
그럼, 다음으로는 우리가 살고 있는 지구의 표면을 닮은 2차원 구를 생각하고, 그 위에 삼각형 \(\Delta\)를 그리려고 합니다. 그러기 위해 먼저 구 위의 삼각형이란 무엇인지 알아볼 필요가 있습니다. 먼저 구를 생각하기 위해서 3차원 유클리드 공간에 주어진 내적을 생각합니다. 즉, 두 개의 벡터 \({\bf v} = (v_1,v_2,v_3)\)와 \({\bf w} = (w_1,w_2,w_3)\)가 있을 때, 내적 \({\bf v} \cdot {\bf w}\)는 다음과 같이 계산할 수 있습니다.
\(v_1 w_1 + v_2 w_2 + v_3 w_3\)
이 때 벡터 중에서 자기 자신과 내적을 취했을 때의 값이 \(1\)이 되는 것들을 모아놓은 집합이 구가 됩니다. 그럼, 과연 유클리드 평면에서의 직선과 같은 역할을 하는 구 위의 ‘직선’은 무엇일까요? 사실 원점을 지나는 2차원 평면과 구가 만나는 점들을 모아 놓은 대원이 구 위의 ‘직선’이 됩니다. 그럼, 이번에는 이러한 ‘직선’으로부터 어떻게 반사를 얻을 수 있을까요? 3차원 유클리드 공간에 구의 ‘직선’ \(\ell\)을 포함하는 원점을 지나는 2차원 평면을 \(P\)라고 하면, ‘직선’ \(\ell\)로부터 얻게 되는 반사 \(R\)은 평면 \(P\)로부터 얻을 수 있는 반사를 구 위에 한정해서 보면 됩니다. 즉, 구 위의 한 점 \({\bf v}\)을 반사하여 얻어지는 점 \(R({\bf v})\)는 다음과 같이 계산할 수 있습니다.
\(R({\bf v}) = {\bf v} – 2 \left( \frac{{\bf v} \cdot {\bf w}}{{\bf w} \cdot {\bf w}} \right) {\bf w}\)
여기서, \({\bf w}\)는 평면 \(P\)에 수직인 영벡터가 아닌 임의의 벡터입니다. 예를 들어, ‘직선’ \(\ell\) 위의 점 \({\bf v}\)는 평면 \(P\)에 있기 때문에 \({\bf w}\)와 수직입니다. 따라서 예상한 것과 같이 \(R({\bf v}) = {\bf v}\)가 됩니다. 반면, \(R({\bf w}) = – {\bf w}\)이므로, ‘직선’ \(\ell\)을 지구의 적도라고 했을 때 북극점에 해당하는 벡터에 반사를 적용하면 남극점으로 이동함을 알 수 있습니다. 또한 구 위의 두 개의 ‘직선’ \(\ell_1\)과 \(\ell_2\)가 점 \({\bf p}\)에서 만날 때 그 두 ‘직선’ 사이의 각을 측정할 수 있습니다. 즉, 각 ‘직선’ \(\ell_i\) 위의 점 \({\bf p}\)에서의 접벡터 \({\bf v}_i\)를 생각하고, 내적을 이용하여 접벡터가 이루는 각을 측정하면 두 ‘직선’ 사이의 각이 됩니다. 그럼 이번에도 유클리드 평면에서와 같이 구 위에 ‘직선’ 세 개로 둘러싸인 삼각형을 생각하고, 특별히 삼각형이 가지는 각의 형태가 \(180^\circ/m\)이라면 반사를 이용하여 구 위의 타일링을 얻을 수 있습니다.
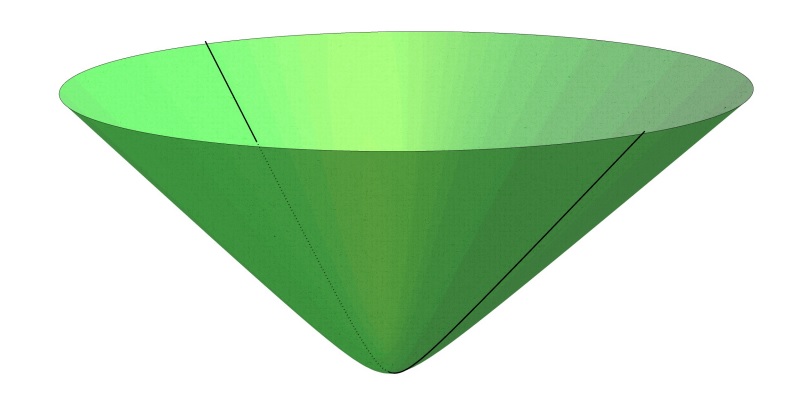
일반적으로는 모든 이면각이 \(180^\circ/m\) 형태를 가지는 \(n\)차원 구 위의 \(n\)-단체로부터, 즉 구의 콕세터 \(n\)-단체로부터 타일링을 얻을 수 있습니다. 여기서 \(n\)-단체는 \((n+1)\)개의 \((n-1)\)차원 면을 가지는 \(n\)차원 다면체를 뜻합니다. 예를 들어, \(2\)-단체는 평면에서의 삼각형을, \(3\)-단체는 \(3\)차원 공간의 사면체를 의미합니다. 이러한 구의 콕세터 \(n\)-단체에는 어떤 것들이 있는지에 대한 답도 콕세터 교수님께서 주셨습니다 [1]. 재미있게도 유클리드 공간에서와 같이 구의 콕세터 \(n\)-단체는 모든 차원에 존재합니다. 하지만, 유클리드 콕세터 \(n\)-다면체와는 다르게 구 위에 존재가능한 콕세터 \(n\)-다면체는 \(n\)-단체 밖에 없습니다. 예를 들어, \(2\)차원 구에는 콕세터 삼각형만 존재할 뿐 콕세터 사각형, 오각형 등은 존재하지 않습니다. 또한, 구의 콕세터 삼각형이 되기 위해서는 세 각의 합이 \(180^\circ\)보다 크다는 사실로부터 구의 콕세터 삼각형을 모두 찾기는 어렵지 않습니다.
자, 그럼 마지막으로 친숙하지는 않지만 흥미로운 쌍곡 공간을 생각해 보려고 합니다. 2차원 구를 만들 때와 비슷하게 2차원 쌍곡 공간을 만들 수 있습니다. 이번에는 3차원 유클리드 공간에 있는 내적을 이용하지 않고 3차원 공간에 로런츠 내적을 정의합니다. 즉, 두 개의 벡터 \({\bf v} = (v_1,v_2,v_3)\)와 \({\bf w} = (w_1,w_2,w_3)\)가 있을 때, 로런츠 내적 \( \langle {\bf v}, {\bf w} \rangle\)은 다음과 같습니다.
\(- v_1 w_1 + v_2 w_2 + v_3 w_3\)
그럼, 벡터 \({\bf v}\) 중에서 자기 자신과 로런츠 내적을 취했을 때의 값이 \(-1\)이 되는 것을 모아 놓으면 두 개의 연결된 성분을 가지는 쌍곡면이 만들어지는데, 그 중 첫 번째 좌표 \(v_1\)이 양수인 것들만 모아놓으면 2차원 쌍곡 공간을 얻을 수 있습니다. 쌍곡 공간에 삼각형을 그리기 위해서 구면에서처럼 쌍곡 공간에서의 ‘직선’을 먼저 생각해 보아야 합니다. 즉, 구에서의 ‘직선’이 원점을 지나는 2차원 평면과 구가 만나는 점들을 모아 놓은 대원이었던 것처럼, 쌍곡 공간에서의 ‘직선’은 원점을 지나는 2차원 평면과 쌍곡 공간이 만나는 점들을 모아 놓은 곡선이 됩니다. 물론 공집합이 아닌 곡선들만 고려합니다.
그럼 이러한 쌍곡 공간의 ‘직선’ \(\ell\)로부터 반사 \(R\)는 어떻게 얻을 수 있을까요? 구에서 반사를 만든 방법을 돌이켜보면 다음과 같이 쌍곡 공간에서의 반사를 만드는 것이 자연스러워 보입니다. 즉, ‘직선’ \(\ell\)에 대응하는 원점을 지나는 2차원 평면 \(P\)가 있을 때, 평면 \(P\)에 로런츠 수직인 영벡터가 아닌 벡터 \({\bf w}\)를 생각합니다. 이 때, 쌍곡 공간 위의 한 점 \({\bf v}\)를 반사하여 얻어지는 점 \(R({\bf v})\)는 다음과 같이 정의할 수 있습니다.
\(R({\bf v}) = {\bf v} – 2 \frac{ \langle {\bf v}, {\bf w} \rangle }{ \langle {\bf w}, {\bf w} \rangle } {\bf w}\)
또한 쌍곡 공간 위의 두 개의 ‘직선’ \(\ell_1\)과 \(\ell_2\)가 한 점 \({\bf p}\)에서 만날 때, 그 두 ‘직선’ 사이의 각은 로런츠 내적을 이용하여 측정할 수 있습니다.
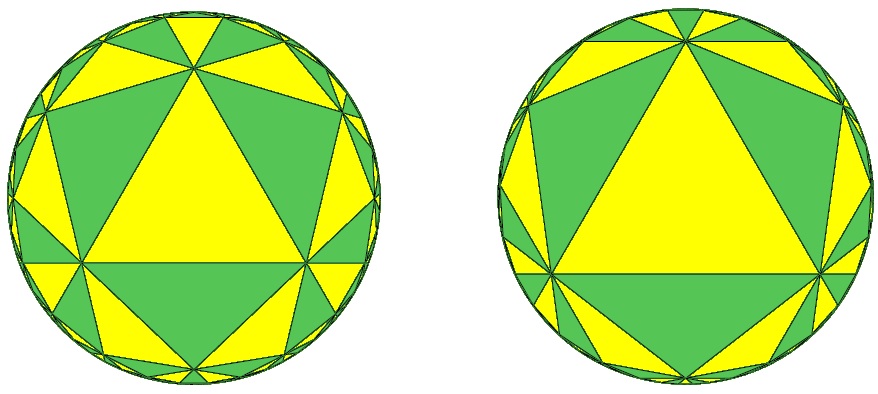
그럼 이번에도 앞에서와 같이 2차원 쌍곡 공간 위에 삼각형 \(\Delta\)가 \(180^\circ/m\) 형태의 각을 가진다면 즉 쌍곡 콕세터 삼각형인 경우에, 반사를 이용하여 쌍곡 공간의 타일링을 얻을 수 있는 것입니다. 여기서 놀라운 사실은 쌍곡 공간에는 삼각형 또는 사각형 이외에도 쌍곡 콕세터 오각형, 육각형 등이 존재합니다. 예를 들어 \(n\)이 4보다 크다면 모든 각이 \(90^\circ\)인 \(n\)각형이 존재합니다. 이렇듯 2차원 쌍곡 공간에는 구 또는 유클리드 공간보다 더 다양한 타일링을 얻을 수 있는 것입니다! 아래의 왼쪽 그림은 세 각이 \((45^\circ,45^\circ,45^\circ)\)인 쌍곡 콕세터 삼각형으로부터, 오른쪽 그림은 세 각이 \((36^\circ,36^\circ,36^\circ)\)인 쌍곡 콕세터 삼각형으로부터 얻은 2차원 쌍곡 공간의 타일링을 3차원 공간의 원점에서 바라본 모습입니다.
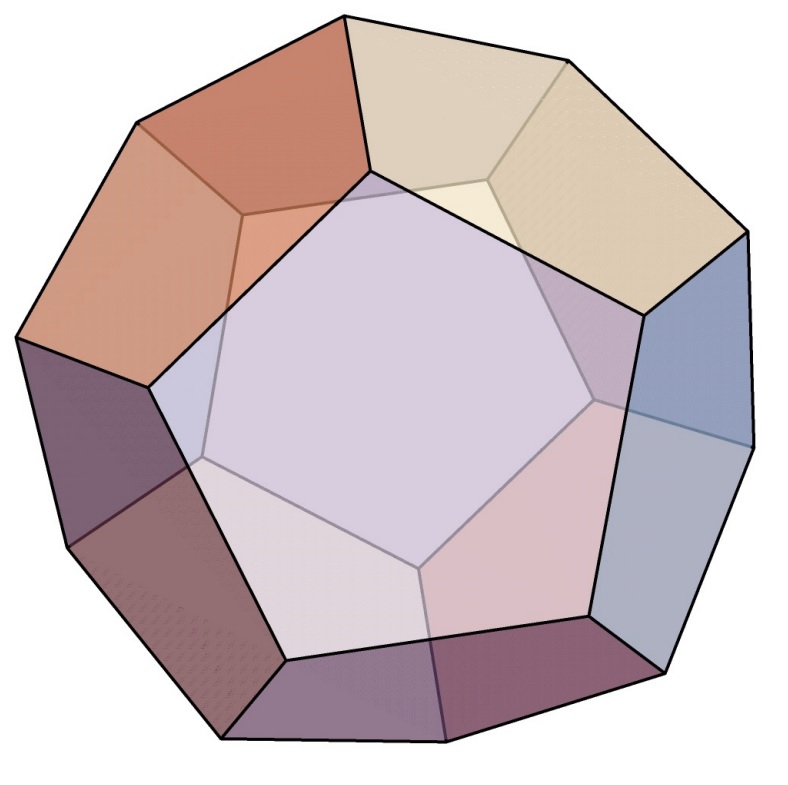
또한 3차원 공간을 살펴보면 구에는 사면체, 유클리드 공간에는 사면체, 삼각기둥, 또는 정육면체 만이 존재할 수 있는데 반하여 쌍곡 공간에는 다양한 콕세터 다면체가 존재합니다. \(3\)차원 쌍곡 공간에 존재 가능한 콕세터 \(3\)-다면체는 어떤 것들이 있는지도 잘 알려져 있습니다 [2],[3]. 예를 들어 모든 각이 \(90^\circ\)인 십이면체도 존재합니다!
그렇기 때문에 \(2\)차원 또는 \(3\)차원과 같이 저차원에서는 구 또는 유클리드 공간보다 쌍곡 공간이 더 흥미롭다고 이야기합니다. 한편, 구와 유클리드 공간에서는 모든 차원에 콕세터 다면체가 존재할 수 있는데 반하여 쌍곡 콕세터 \(n\)-다면체는 놀랍게도 차원 \(n\)이 \(29\)보다 클 수 없습니다 [4]. 지금까지 알려진 가장 차원이 큰 쌍곡 콕세터 다면체의 차원은 8차원입니다 [5]. 마지막으로 아직 알려지지 않은 다음의 질문을 던지며 이 글을 마칠까 합니다. 과연, \(n\)이 9와 29 사이일 때 쌍곡 콕세터 \(n\)-다면체가 존재하여 반사를 이용한 \(n\)차원 쌍곡 공간의 타일링을 만들 수 있을까요?
참고문헌
- H. S. M. Coxeter. Discrete groups generated by reflections. Ann. of Math. (2), 35(3):588-621, 1934.
- F. Lann\('e\)r. On complexes with transitive groups of automorphisms. Comm. S\('e\)m., Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.], 11:71, 1950.
- E. M. Andreev. On convex polyhedra in Lobachevskil spaces. Math. USSR, Sb., 10(3):413-440, 1971.
- E. B. Vinberg. Absence of crystallographic groups of reflections in Lobachevskil spaces of large dimension. Trudy Moskov. Mat. Obshch., 47:68-102, 246, 1984.
- V. O. Bugaenko. Arithmetic crystallographic groups generated by reflections, and
reflective hyperbolic lattices. In Lie groups, their discrete subgroups, and invariant theory, volume 8 of Adv. Soviet Math., pages 33-55. Amer. Math. Soc., Providence, RI, 1992.