비국소non-local 게임은 심판이 출제한 문제를 두 명의 플레이어1, Alice와 Bob이 풀어내는 협동게임이다. 다만 문제를 구성하는 정보가 Alice와 Bob에게 각각 제한적으로 공개된다는 것이 흥미로운 점이다. 예를 들어 심판이 Alice에게 5만 원을 50%의 확률로, Bob에게도 5만 원을 50%의 확률로 지급한 후 지급액 총액이 10만 원 이상일지 묻는다고 하자. 이때 Alice와 Bob 모두 정답을 말해야 하는데 서로 정보를 교환할 수 없다면 곤혹스러운 경우가 생긴다. Alice의 입장에서 5만 원을 지급받지 못했다면 총액이 10만 원 미만이므로 고민할 필요가 없지만, 만약 5만 원을 지급받았다면 총액이 5만 원일 수도 있고, 10만 원일 수도 있기 때문이다. 따라서 제한된 정보만으로는 완벽한 결론을 내릴 수 없고, 이는 Bob 또한 마찬가지이다.
독자분들은 이미 75%의 승률을 확보하는 방법을 염두에 두고 있을 터인데, 위와 같은 게임의 최대승률과 최적전략을 고민하는 것이 비국소 게임에서의 주된 관심사이다. 각 플레이어에게는 국소적 전략만이 허용되지만, 이들의 협동전략과 이에 따른 승률은 모든 상황을 아우를 수 있도록 합성계composite system에서 이해하여야 하기에 비국소 게임이라 불린다. 이때 Alice와 Bob에게 양자전략이 허용될 경우 승률을 높일 수 있는지가 중요한 주제이다. 실제로 우월양자전략을 찾을 수 있는지에 대한 논의가 양자역학에서 비국소성 개념을 다룰 때 등장하는 벨Bell 부등식의 성립 여부와 맥락을 같이 한다.
양자전략을 구성하는 두 요소는 양자얽힘quantum entanglement과 양자측정quantum measuremet이다. 이때 Alice와 Bob에게 주어지는 양자측정을 행렬대수의 텐서곱tensor product모델에서 허용하는 경우와 이보다 일반적인 교환작용소commuting operator 모델에서 허용하는 경우를 비교하는 것은 아주 중요한 문제이다. 실제로 칠레슨Boris Tsirelson은 후자에서 얻어낼 수 있는 양자전략들이 전자에 의해 근사될 것이라 주장하였고[1,2], 이는 칠레슨Tsirelson 추측이라 일컬어지며 양자정보이론quantum information theory 분야의 주요 난제로 여겨져 왔다.
2010년대 초에 밝혀진 놀라운 사실은 칠레슨Tsirelson 추측이 상당히 다른 분야인 작용소대수operator algebra분야의 가장 중요한 난제 중 하나였던 콘의 임베딩Connes embedding 문제와 동등하다는 것이다.[3,4,5] 콘의 임베딩Connes embedding 문제의 역사는 필즈메달 수상자인 알랭 콘Alain Connes의 1976년 Ann. of Math. 논문[6]으로 거슬러 올라가며, 그간 수많은 노력이 있었지만 오랜 시간 난제로 남아있었다.
2020년 작용소대수 분야에서 가장 놀라운 소식 중 하나는 Arxiv에 등장한 한 초안이었다.[7] 이 초안은 양자 계산복잡도 이론quantum complexity theory을 응용하여 칠레슨Tsirelson 문제에 반례가 있음을 설명하였는데, 이는 콘의 임베딩Connes embedding 문제 또한 해결하였음을 의미하기 때문에 대단히 중요한 결과이다. 이에 관한 보다 자세한 내용은 [7]의 저자 중 한 명인 토마스 비딕Thomas Vidick의 QIP2021 기조강연 영상을 참조할 수 있다. 이번 글의 목표는 비국소 게임과 양자전략을 보다 구체적으로 이해할 수 있도록 돕고, 텐서곱 모델과 교환작용소 모델의 차이를 설명하여 칠레슨Tsirelson 추측에 대한 이해를 돕는 것이다. 대표적인 비국소 게임 중 하나인 그래프 색칠 게임을 먼저 살펴보도록 하자.
1. 그래프 색칠 게임과 비국소 게임
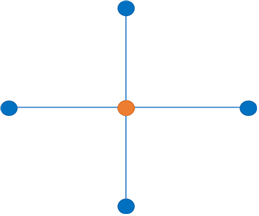
그래프 색칠 문제는 주어진 그래프의 꼭짓점마다 색을 칠하는데, 인접한 두 꼭짓점은 다른 색으로 칠할 수 있는지에 관한 그래프이론 문제이다. 예를 들어 아래의 그래프를 살펴보면,
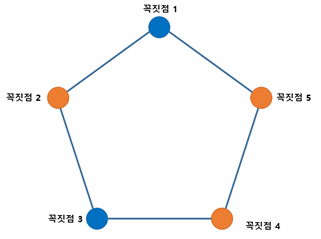
두 가지 색을 이용하여 주어진 조건을 만족하도록 칠할 수 있음을 알 수 있다. 이러한 의미에서 위의 그래프의 채색수chromatic number를 2라 한다. 한편 아래의 그래프
는 세 가지 색으로 칠할 수 있는데, Alice와 Bob이 [그림2]를 공유하고 있다면 어떠한 검증에도 모순 없이 답을 할 수 있다. 예를 들어 심판이 검증을 위해 Alice에게 “꼭짓점 3은 무슨 색을 칠했나요?”라는 메시지를 보내고, Bob에게 “꼭짓점 4는 무슨 색을 칠했나요?”라는 메시지를 보냈다고 하자. 이때 Alice와 Bob은 사전에 공유한 [그림2]를 살펴보고 각각 “꼭짓점 3은 파란색을 칠했습니다.”와 “꼭짓점 4는 주황색을 칠했습니다.”라는 모순 없는 답변을 제출할 수 있다. 만약 심판이 Alice와 Bob에게 같은 메시지 “꼭짓점 5는 무슨 색을 칠했나요?”라는 메시지를 보낸다면, 공유하였던 [그림2]를 살펴본 후 각각 “꼭짓점 5는 연두색을 칠했습니다.”라는 모순 없는 답변을 제출할 수 있다.
한 가지 흥미로운 점은 위의 검증과정을 살펴보면 Alice와 Bob이 완벽한 답을 갖고 있지 않더라도 심판의 질문에 때로는 모순 없는 답변을 제출할 수 있다는 것이다. 예를 들어 Alice와 Bob이 아래와 같이 채색된 [그림3]을 공유하고, 두 가지 색만을 사용하여 모순 없이 채색하였다고 심판에게 주장한다고 하자.
이에 미심쩍어하는 심판이 검증을 위해 Alice에게 “꼭짓점 2는 무슨 색을 칠했나요?”라는 메시지를 보내고 Bob에게 “꼭짓점 3은 무슨 색을 칠했나요?”라는 메시지를 보낸다면, Alice와 Bob은 사전에 공유하였던 [그림3]을 토대로 “꼭짓점 2는 주황색을 칠했습니다.”와 “꼭짓점 3은 파란색으로 칠했습니다.”라는 모순 없는 답변을 제출할 수 있다. 이 경우에는 심판을 속일 수 있는 것이다. 하지만 운이 좋지 않게도, 심판이 Alice에게 “꼭짓점 5는 무슨 색을 칠했나요?”라는 메시지를 보내고, Bob에게 “꼭짓점 4는 무슨 색을 칠했나요?”라는 메시지를 보내는 경우에는 모순된 답을 제출하게 되므로 거짓 주장이 적발됨을 알 수 있다.
이때 주목할 점은 심판이 무작위로 만들어낼 수 있는 질문의 쌍 “Alice, 꼭짓점 \(i\)는 무슨 색으로 칠했나요?”와 “Bob, 꼭짓점 \(j\)는 무슨 색으로 칠했나요?”는 25가지인데, 이 질문들에 대하여 Alice와 Bob이 모순적인 답을 제출하는 경우는 2가지뿐이라는 것이다. 즉 92%의 확률로 모순 없는 답을 제출하게 된다. 꼭짓점 \(i\)와 \(j\)가 인접한 경우만을 묻는다 하여도 80% 확률로 모순 없는 답을 제출하게 된다.
비국소 게임은 위와 같은 상황을 일반화한 것인데, 게임의 승리 및 패배 규칙이 정해져 있을 때 Alice와 Bob이 최대승률을 확보하기 위한 전략을 사전에 공유한 뒤 심판의 질문에 대응하는 게임이다. 이를 보다 수학적으로 표현하자면, 승리 및 패배 규칙은 함수 \(V:O \times O \times I \times I \rightarrow \{ 0,1 \}\)로 나타낼 수 있다. 이때 \(I\)는 심판이 사용하는 입력input 메시지들의 집합이며, \(O\)는 플레이어들이 회신하는 출력output 메시지들의 집합이다.
위에서 살펴본 [그림3]의 경우에는 \(I\)가 그래프의 꼭짓점들의 집합이므로 \(I=\{1,2,3,4,5\}\)이고 \(O\)는 채색에 사용한 색의 집합이므로 \(O=\{주황, 파랑\}\)임을 알 수 있다. 이때 \(V\)는 승리 및 패배 규칙을 나타내어야 하는데, 승리하는 경우는 \(V(주황,파랑,2,3)=1\) 그리고 패배하는 경우는 \(V(주황,주황,4,5)=0\) 등으로 표현한다. 또한 Alice와 Bob이 사전에 준비한 전략은 다음의 함수,
\(f:I \rightarrow O, \begin{cases} f(1)=파랑\\f(2)=주황\\f(3)=파랑\\f(4)=주황\\f(5)=주황\end{cases}\)
를 이용하여 각 입력 메시지에 대응되는 출력 메시지를 심판에게 제출하는 것이다.
따라서 위의 게임은 규칙함수 \(V\)와 전략함수 \(f\)로 구성되며, 각 라운드마다 심판이 Alice에게 메시지 \(x\), Bob에게 메시지 \(y\)를 보내는 것으로 시작한다. 이후 Alice가 심판에게 메시지 \(a=f(x)\), Bob이 심판에게 메시지 \(b=f(y)\)를 제출하는 것으로 진행되며, \(V(a,b,x,y)=1\)을 만족할 경우 승리한 것으로 \(V(a,b,x,y)=0\)일 경우 패배한 것으로 이해한다.
2. CHSH 게임과 확률적 접근
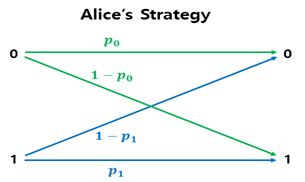
보다 일반적으로는 Alice와 Bob이 동일한 전략함수 \(f\)를 사용할 필요가 없고, 답변 또한 확률적으로 선택하여 제출하는 것이 가능하다. 이를 벨Bell 부등식을 이해하는 방식 중 하나로 널리 알려진 CHSH2 게임을 통해 살펴보자. 이 게임은 심판이 Alice와 Bob에게 각각 0 또는 1을 무작위로 택하여 메시지로 보내고, Alice와 Bob은 각각 주어진 메시지 \(x,y\)에 대하여 등식 \(a+b=x \cdot y (mod 2)\)가 성립하도록 심판에게 메시지 \(a,b\)를 회신하면 승리하는 게임이다. 이때 Alice가 취할 수 있는 확률적 전략을 다음과 같이 나타낼 수 있다.
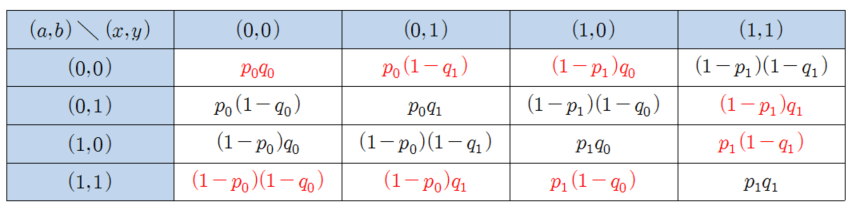
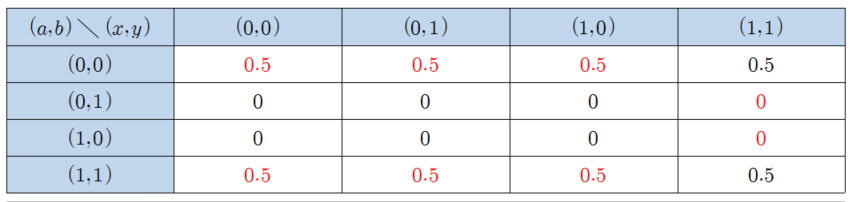
즉 메시지 \(x=0\)을 받으면 심판에게 확률 \(p_0\)로 메시지 \(a=0\)을, 그리고 확률 \(1-{p_0}\)로 메시지 \(a=1\)을 보내는 것이다. 또한 메시지 \(x=1\)을 받으면 심판에게 확률 \(1-{p_1}\)으로 메시지 \(a=0\)을, 확률 \(p_1\)으로 메시지 \(a=1\)을 보내는 전략을 택하는 것이다. 마찬가지로 Bob 또한 확률 \(q_0\)와 \(q_1\)을 이용하여 주어지는 메시지 \(y\)에 대하여 회신할 메시지 \(b\)를 택하는 본인의 확률적 전략을 수립할 수 있다. 이에 따라 심판의 초기 메시지 \((x,y)\)에 따른 조건부 확률을 분석한 결과는 [그림5]와 같이 주어진다.
주어진 승리조건인 등식 \(a+b=x \cdot y (mod2)\)이 성립하는 경우가 빨간색으로 칠해져 있는데, 각 경우의 확률의 합이 \(p_0, p_1, q_0, q_1\)에 대한 4변수 함수로 나타난다. 핵심은 이 함수의 최댓값이 3이라는 것인데, 이는 초기 메시지 \((x,y)\)가 무작위로 주어질 때 Alice와 Bob의 최대 평균 승률이 75%임을 의미한다. 이때 75%를 달성하는 최적전략은 유일하지 않은데, 예를 들어 \((p_0, p_1, q_0, q_1)\)이 \((1, 1, q_0, 0)\) 꼴로 주어질 때마다 초기 메시지 \((x,y)\)에 따른 승률이 각각 \(q_0, 1, 1-{q_0}, 1\)로 주어져 평균 승률 75%가 달성됨을 알 수 있다.
3. CHSH 게임과 양자전략
앞에서는 곱product 확률분포만을 고려하여 평균 승률을 논하고 있는데, 물론 이에 해당하지 않는 확률분포 또한 존재한다. 예를 들어 아래의 분포
는 곱 확률분포로 표현되지 않는 대표적인 예이다. 흥미로운 사실은 Alice와 Bob이 소위 ‘얽힌 양자상태entangled quantum state‘를 공유하고 있다면, 적절히 택한 양자측정을 이용하여 우월전략을 찾아낼 수 있다는 점이다. [그림6]의 경우는 실제로 최대로 얽힌maximally entangled 양자상태로부터 얻어낼 수 있는 전략 중 하나이기는 하지만, 평균 승률이 75%이므로 우월전략이라고 할 수는 없다.
CHSH 게임에서 Alice와 Bob이 양자측정을 택하는 가장 간단한 방법은 심판으로부터 받은 메시지가 \((x,y)\)인 경우에 사용할 2차원 단위벡터 \(\xi _{0}^{(x)}\)와 \( \eta _{0}^{(y)}\)를 각각 준비하는 것이다. 이때 \(\xi _{0}^{(x)}\)에 수직인 단위벡터 \(\xi _{1}^{(x)}\), 그리고 \( \eta _{0}^{(y)}\)에 수직인 단위벡터 \( \eta _{1}^{(y)}\)를 생각할 수 있으며 여기까지가 양자측정을 준비하는 단계이다. 이후 최대로 얽힌 양자상태와 위의 양자측정을 이용하면 입력메시지 \((x,y)\)가 주어질 때마다 Alice와 Bob은 메시지 \((a, b)\)를 \( \frac{1}{2} \cdot | \xi _{a}^{(x)} \cdot \eta _{b}^{(y)} | ^{2}\)의 확률로 출력하여 심판에게 회신할 수 있다. 만약 Alice와 Bob이 입력메시지 \((x, y)\)에 무관하게 양자측정을 단순히 \(\xi _{0}^{(x)} = \eta _{0}^{(y)} = \begin{bmatrix}1 \\ 0 \end{bmatrix}\)과 \(\xi _{1}^{(x)} = \eta _{1}^{(y)} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\)로 택하는 경우에는 [그림6]과 같이 주어지는 확률분포를 얻게 된다.
따라서 75%를 초과하는 우월전략을 얻기 위해서는 보다 정교하게 양자측정을 택하여야 하는데, Alice가 \(x=0\)일 경우 사용할 단위벡터 \(\xi_{0}^{(0)} = \begin{bmatrix}1 \\ 0 \end{bmatrix}\)와 \(x=1\)일 경우 사용할 단위벡터 \(\xi _{0}^{(1)} = \begin{bmatrix} cos( \pi /4) \\ sin( \pi /4) \end{bmatrix}\)를 준비하였다고 하자. 또한 Bob이 \(y=0\)일 경우 사용할 단위벡터 \(\eta _{0}^{(0)} = \begin{bmatrix} cos( \pi /8) \\ sin( \pi /8) \end{bmatrix}\)와 \(y=1\)일 경우 사용할 단위벡터 \(\eta _{0}^{(1)} = \begin{bmatrix} cos( – \pi /8) \\ sin( – \pi /8) \end{bmatrix}\)를 준비한다면, 입력메시지 \((x,y)\)가 주어질 때마다 Alice와 Bob은 출력메시지 \((a,b)\)를 아래와 같은 확률로 심판에게 회신할 수 있다.
따라서 입력 메시지 \((x,y)\)에 무관하게 항상 \(cos^2( \pi /8)\), 약 85.36%의 승률을 확보할 수 있음을 살펴볼 수 있고, 이는 우월전략이라 할 수 있다.
4. 교환작용소 모델과 칠레슨Tsirelson 문제
CHSH 게임은 심판이 입력 가능한 메시지의 종류가 2개이고 Alice와 Bob이 각각 심판에게 회신 가능한 출력메시지의 종류도 2개였는데, 일반적인 비국소 게임에서는 입력메시지의 종류가 \(m\)개이고 출력메시지의 종류가 \(k\)개라 가정한다. 이때 얽힌 양자상태와 양자측정을 동원하여 다양한 양자전략을 만들어내는 것은 중요한 문제이고, 실제로 CHSH 게임에서 입력메시지 \((x,y)\)에 따라 Alice와 Bob이 각각 단위벡터 \(\xi _{a}^{(x)}\)와 \( \eta _{b}^{(y)}\)를 어떻게 택하는지가 승률을 결정하는 중요한 역할을 하였다. 한 가지 유념할 것은 확률을 벡터 \(\xi _{a}^{(x)}\)와 \(\eta _{b}^{(y)}\)의 내적값으로서 얻어내기 때문에, \(\xi _{a}^{(x)}\)와 \( \eta _{b}^{(y)}\)의 차원이 고정되어 있을 필요가 없다는 점이다. 즉 가능한 입력메시지의 개수 \(m\)과 출력메시지의 개수 \(k\)가 고정되어 있을 때, 양자측정을 구성할 단위 벡터들을 임의의 차원에서 택할 수 있다는 것이다.
이때 단위 벡터들만으로는 모든 양자측정을 나타낼 수 없는데, 일반적으로는 입력메시지 \((x,y)\)에 대하여 사용할 행렬 \(M_{a}^{(x)}\)와 \(N _{b}^{(y)}\)를 Alice와 Bob이 각각 준비하여야 한다. 벡터의 경우와 마찬가지로 이 행렬들은 임의의 유한차원에서 택할 수 있는데, 이렇듯 행렬로 구성된 임의의 양자전략으로부터 얻어낼 수 있는 조건부확률의 집합을 \(C_q(k,m)\)으로 나타낸다. 일반적으로 \(C_q(k,m)\)의 원소를 행렬 텐서곱 모델로부터 얻어진다고 하는데, 그 이유는 양자측정이 \(\{M_{a}^{(x)} \bigotimes N_{b}^{(y)}\}_{a,b}\)꼴이기 때문이다.3
이때 주어지는 조건부 확률은 입력메시지 \((x,y)\)가 주어졌을 때 메시지 \((a,b)\)를 회신할 확률을 나타내어야 하므로 \(a,b,x,y\) 총 \(k^2, m^2\)개의 변수로 갖는 함수라 할 수 있다. 따라서 유클리드공간 \(\mathbb{R}^{k^2,m^2}\)의 원소라 할 수 있고, 이러한 원소들의 모임인 집합 \(C_q(k,m)\)는 유클리드공간 \(\mathbb{R}^{k^2,m^2}\)의 부분집합이다. 이의 닫힘closure을 \(C_{qa}(k,m)\)라 표기하는데, 이때 \(C_{qa}(k,m)\)의 원소들은 행렬 텐서곱 모델로부터 얻을 수 있는 원소들로 근사 가능하다고 한다.
위의 내용을 정리해보자면 가능한 입력메시지의 개수 \(m\)과 출력메시지의 개수 \(k\)가 고정되었을 때, 행렬을 이용한 양자전략을 통해 얻을 수 있는 혹은 근사 가능한 조건부확률들의 모임을 \(C_{qa}(k,m)\)로 정의한 것이다. 이때 주목해야할 것은 양자측정이 반드시 텐서곱 \(\{M_{a}^{(x)} \bigotimes N_{b}^{(y)}\}_{a,b}\)꼴로 주어질 필요가 없다는 점이다. 이에 대하여 보다 일반적 방법을 제공하는 것이 교환작용소 모델인데 이는 실제로 작용소대수 이론에서 핵심적인 역할을 하며, 이외에도 대수적 양자장론 등에 이용되는 개념이다.[8] 또한 텐서곱 모델은 유한차원인 경우만을 고려하지만 교환작용소 모델에서는 무한차원 힐버트Hilbert 공간에 작용하는 작용소 또한 허용한다. 따라서 교환작용소 모델이 보다 많은 양자전략을 제공하여 평균 승률을 높일 수 있을 것이라 기대해볼 수 있는데, 주어진 상황을 다시 한번 정리해보자면 아래와 같다.
가능한 입력메시지의 개수 \(m\)과 출력메시지의 개수 \(k\)가 고정되었을 때 행렬만을 이용한 텐서곱 모델로부터 얻을 수 있는 조건부확률들이 모임을 \(C_{qa}(k,m)\)라 표기하였고, 무한차원 경우도 허용한 교환작용소 모델로부터 얻을 수 있는 조건부확률들의 모임을 \(C_{qc}(k,m)\)이라 표기한다. 이때 포함관계 \(C_{qa}(k,m)\) ⊆ \(C_{qc}(k,m)\)가 성립하는데, 임의의 \(k,m\)에 대하여 등호가 성립하는지 여부가 바로 칠레슨Tsirelson 문제이다.
1993년 칠레슨Tsirelson은 [1]에서 두 집합이 실제로 일치한다고 주장하였는데, 2006년에 철회하였으며 이를 [2]에서 미해결 문제로 제시하였다. 이후 2010년대 초 일련의 연구들 [3,4,5]를 통해 칠레슨Tsirelson 추측이 작용소대수에서의 가장 중요한 난제 중 하나였던 콘의 임베딩Connes embedding 문제와 동등하다는 것이 밝혀졌고, 최근 Arxiv에 게재된 초안 [7]은 칠레슨Tsirelson 추측에 대하여 반례가 존재함을 설명하고 있다. 즉 \(C_{qa}(k,m)\) ⊊ \(C_{qc}(k,m)\)임을 보인 것인데, 이는 비국소 게임의 관점에서는 유한차원 행렬 텐서곱 모델로부터 얻어낼 수 있는 양자전략만으로는 근사 불가능한 교환작용소 모델에서의 양자전략이 있음을 의미하고, 또한 콘의 임베딩Connes embedding 문제에 대한 해답 또한 제시함으로써 작용소대수 분야의 새로운 지평을 열었다고 할 수 있다. 어느 한 사람만의 노력으로 이루어지지 않은 이 쾌거가 작용소대수 연구자들이 새로이 나아갈 길의 초석이기를 기원한다.
참고문헌
- B.S. Tsirelson, Some results and problems on quantum Bell-type inequalities, Hadronic Journal Supplement 8 (1993), 329–345.
- B.S. Tsirelson, Bell inequalities and operator algebras, problem statement for website of open problems at TU Braunschweig (2006), available at here.
- T. Fritz, Tsirelson’s problem and Kirchberg’s conjecture, Rev. Math. Phys., 24 (2012),
1250012, 67 pp. - M. Junge, M. Navascues, C. Palazuelos, D. Perez-Garcia, V.B. Scholz and R.F. Werner,
Connes embedding problem and Tsirelson’s problem, J. Math. Phys., 52 (2011), 012102,
12 pp. - N. Ozawa, About the Connes embedding conjecture. Jpn. J. Math. 8, 147–183 (2013).
- A. Connes, Classification of injective factors. Cases Ⅱ1,Ⅱ∞, Ⅲλ, λ≠1. Ann. of Math. (2) 104 (1976), no. 1, 73–115.
- Z. Ji, A. Natarajan, T. Vidick, J. Wright, and H. Yuen. "Mip*= re." arXiv preprint arXiv:2001.04383 (2020).
- R. Haag, and D. Kastler, An Algebraic Approach to Quantum Field Theory, Journal of Mathematical Physics 5 (1964), no. 7, 848–861.