마음속으로 1부터 1157920892373161954235709850086879078528375642790749
04382605163141518161494336 사이에 있는 자연수를 하나 골라보자. 이 숫자는 다른 사람에게 알려주지 않도록 하자. 선택한 순간, 이 수를 비밀번호로 갖는 당신의 비트코인 주소, 즉 계좌번호도 결정되었기 때문이다. 나는 이 글을 준비하며 연습 삼아 이 비밀번호에 해당하는 숫자를 하나 선택했다. 이로부터 결정된 비트코인의 주소는 bc1qrkzwa4mczc5zlnvqn
eew6pcfn3rjrc37q2w2a5이다. 이 주소에 얼마의 비트코인이 있는지는 공개된 장부를 통해 확인할 수 있다. 이 장부를 비트코인의 블록체인이라 하는데, 블록체인의 데이터를 인터넷에서 쉽게 확인할 수 있도록 도와주는 웹사이트들도 있다. 가령 이 링크를 방문하면
(https://www.blockchain.com/btc/address/bc1qrkzwa4mczc5zlnvqneew6pcfn3rjrc37q2w2a5)
이 주소의 거래 내역을 볼 수 있다. 비트코인을 가지고 있는 사람은 이 주소로 비트코인을 보낼 수 있다. 만약 선택된 비밀번호가 무엇인지 알아낼 수 있는 사람이라면, 누구의 허락 없이도 조용히 이 주소에 있는 비트코인을 자신의 주소로 옮길 수 있다. 비밀번호의 소유자는 곧 비트코인의 소유자이다.
사람이 숫자 하나를 고르는 것은 누구의 허락이 있어야 하는 일일 수 없다. 그 숫자로부터 정해진 방식대로 약간의 계산을 하면 주소가 탄생한다. 따라서 개개인이 비트코인 계좌를 만드는 일을 누군가가 막는다는 것은 실질적으로 불가능하다. 사람이 숫자 하나를 선택할 권리와 계산을 할 권리를 제약할 방법이 없다면 말이다.
마음속으로 숫자를 하나 고른 순간 계좌가 결정된다는 말은 선뜻 이해되지 않는다. 보통 우리가 저금하고 거래를 할 수 있는 은행 계좌를 만든다고 하면, 당연히 은행을 방문하거나 아니면 앱과 같은 은행이 제공하는 다른 수단을 이용해야 한다. 은행에서 우리의 신원을 확인하고 계좌 발급을 진행해 준 이후에야, 우리는 계좌번호도 받고 계좌의 비밀번호를 설정할 수 있다. 그런데 은행이 없어도 혼자서 계좌를 만들어 거래를 시작할 수 있다는 것은 도대체 무슨 말일까?
이 글에서는 비밀번호에 해당하는 숫자에서 시작해 비트코인의 주소가 만들어지는 과정의 배후에 있는 수학에 대해 이야기해보려 한다. 그 핵심은 ‘유한체 위의 타원곡선에는 가환군 구조가 존재한다’라는 짧은 문장으로 요약할 수 있다. 수학자가 아니라면 이런 말은 외계어에 가깝지만, 약간의 인내심을 가지면 이를 이해하는 일이 불가능한 것도 아니다. 수학자 서지 랭이 ‘타원곡선에 대해서는 끝없이 쓸 수 있다’라고 했듯이[1], 타원곡선은 수학적으로 매우 풍부한 소재다. 그 끝없는 이야기의 목록에 비트코인도 한자리를 차지하게 되었다. 이제 비트코인과 타원곡선 사이의 기묘한 관계를 살펴보도록 하자.
유한체
학교의 수학 시간에 우리는 여러 가지 수의 체계에 대해 배운다. 하나, 둘, 셋에서 시작해 자연수, 정수, 유리수, 실수, 복소수와 같은 다양한 개념을 만나게 된다. 유한체는 사실 이들보다 더 간단한 것이지만, 중고등학교에서 가르치는 것은 아니므로 이런 단어를 처음 들었다고 해도 크게 이상한 일은 아니다.
수학에서 체field라는 것은 그 안에서 덧셈, 뺄셈, 곱셈, 나눗셈의 연산이 가능하며, 그 연산이 몇 가지 정해진 규칙을 만족하는 원소들의 모임을 말한다. 가령, 자연수들의 모임은 체가 아니다. 자연수끼리 뺄셈을 하다 보면 음수가 될 수도 있는데, 이는 자연수의 범위를 벗어난다. 정수들 역시 체를 이루지 않는데, 정수를 서로 나누면 2분의 1과 같이 정수의 세계 밖으로 나가는 일이 생기기 때문이다. 하지만 유리수, 즉 분수들의 모임은 그 안에서 사칙연산이 완벽하게 작동한다. 유리수끼리 사칙연산을 해서 유리수 밖의 세계로 나가지 않는다는 말이다. 유리수들은 체의 구조를 이룬다고 할 수 있다. 실수와 복소수도 같은 성질을 갖는다. 그래서 우리는 유리수체, 실수체, 복소수체와 같은 용어를 사용할 수 있다.
유한체는 유한개의 원소만이 있는 체이다. 예를 들어보자. 여기에 0, 1, 2, 3, 4로만 이루어진 수의 세계가 있다. 이 세계의 덧셈과 곱셈은 다음과 같은 표로 이해할 수 있다:
\(\begin{array}{c|ccccc}+ & 0 & 1 & 2 & 3 & 4 \\\hline0 & 0 & 1 & 2 & 3 & 4 \\1 & 1 & 2 & 3 & 4 & 0 \\2 & 2 & 3 & 4 & 0 & 1 \\3 & 3 & 4 & 0 & 1 & 2 \\4 & 4 & 0 & 1 & 2 & 3 \\\end{array}\)
\(\begin{array}{c|ccccc}\times & 0 & 1 & 2 & 3 & 4 \\\hline0 & 0 & 0 & 0 & 0 & 0 \\1 & 0 & 1 & 2 & 3 & 4 \\2 & 0 & 2 & 4 & 1 & 3 \\3 & 0 & 3 & 1 & 4 & 2 \\4 & 0 & 4 & 3 & 2 & 1 \\\end{array}\)
여기에서 덧셈과 곱셈은 등장하는 수를 일단 정수로 여기고 연산을 한 다음, 그 결과를 5로 나눈 나머지로 바꿔 쓰는 것과 같다. 그러니까 \(4+3=2\)가 되는 것은 7을 5로 나눈 나머지가 2이기 때문이다. 마찬가지로 \(3\times 2 = 1\)가 성립하는 것은 6을 5로 나눈 나머지가 1이기 때문이다. 두 수의 뺄셈은 덧셈을 이용해서 이해할 수 있는데, 가령 \(a-b\)를 계산하는 문제는 \(a=b+c\)가 되도록 하는 \(c\)를 찾는 문제로 생각할 수 있다. 나눗셈도 이와 비슷한데 \(b\)가 0이 아닐 때, \(a/b\)를 계산하는 것은 \(a = b\times c\)가 되도록 하는 \(c\)를 찾는 것으로 생각할 수 있다. 이런 방식으로 0, 1, 2, 3, 4만으로 이루어진 수의 세계에 사칙연산이 잘 작동하게 된다.
여기서 사칙연산이 모두 가능한 근본적인 이유는 5가 소수이기 때문인데, 더 일반적으로 임의의 소수 \(p\)에 대해 \(0,1,\dots, p-1\)만으로 이루어진 원소의 개수가 \(p\)인 체 \(\mathbb{F}_p\)를 만들 수 있다. 소수가 아닌, 예를 들면 4로 나눈 나머지로 이루어진 수의 세계에서는 \(2\times 2=0\)과 같이 0이 아닌 두 수를 곱해서 0이 되는 문제가 발생한다. 뒤에서 다시 얘기하겠지만, 비트코인에서는 소수
\(p=2^{256}-2^{32}-977\)
를 원소의 개수로 갖는 유한체를 사용한다.
타원곡선
타원곡선에 대한 이야기에 앞서 먼저 강조할 사실은 타원곡선은 타원이 아니라는 것이다. 중고등학교의 수학·과학 시간에 우리는 타원에 대해 배운다. 타원은 일상의 어디에서나 찾을 수 있다. 주변에 있는 원을 정면에서 바라보는 것이 아니라면, 원은 언제나 눈에 타원의 모습으로 보이게 된다. 지구와 같은 행성이 태양 주위를 타원 궤도로 돌고 있다는 사실의 발견은 지동설에서 만유인력의 법칙으로 이어지는 근대 과학 혁명에서도 중요한 위치를 차지한다. 이런 역사적 사실 덕분에 타원은 인류에게 특별한 의미가 있는 도형이기도 하다.
오래전에 수학자들은 이 타원의 둘레의 길이를 구하는 문제에 관심을 가졌다. 얼핏 사소해 보이는 이 문제에 대한 도전의 과정에서 오랜 시간에 걸쳐 수많은 새로운 수학이 등장하게 된다. 특히 19세기에 타원적분, 타원함수, 타원곡선으로 이어지는 중요한 수학적 발견도 여기서 비롯된 것이다. 타원 둘레의 길이는 타원적분으로 표현되고 타원적분을 이해하려는 노력에서 그 역함수인 타원함수가 발견된다. 타원함수가 복소평면에서 이중주기를 갖는 것으로 이해되자, 이런 함수가 살고 있는 공간으로서의 타원곡선이 발견된다. 타원적분의 이해를 어렵게 만들던 다가 함수multivalued function의 문제는 이 적분을 타원곡선 위에서 이해할 때 완전히 사라지게 된다. 이러한 깨달음의 과정은 복소해석학, 리만곡면론, 다양체의 개념, 보형함수론 등의 형성 및 발전을 자극하며 수학 전체에 큰 영향을 주었는데, 이후 현대수학의 비약적인 발전에 중요한 토대가 되었다. 타원에서 영향받은 이러한 수학에 대한 이야기도 매우 흥미로운 것이다. 이에 대해 관심이 있는 사람들에게는 펠릭스 클라인의 저서 ’19세기 수학의 발전에 대한 강의’[2]를 추천한다.
그렇다면 타원곡선이란 무엇일까? 타원곡선은 체 \(K\)의 주어진 원소 \(a, b\)에 대하여 (이 때, \(4a^3 + 27b^2 \neq 0\)), 방정식
\(y^2 = x^3+ ax+b\)
을 만족하는 점 \((x,y)\in K^2\)들의 모임이다. 타원적분과 이런 방정식의 복소수해로 기술되는 공간의 필연적 관계 때문에, 여기에 타원곡선이라는 이름이 붙게 되었다. 비트코인과 관련된 타원곡선은 \(a=0,\, b=7\)인 경우에 해당한다. 다시 말해, 비트코인 시스템은 \(y^2 = x^3+ 7\)이라는 특정한 방정식을 사용하고 있다.
앞으로의 이야기에서는 \(a,b\)가 정수라고 가정한다. 이런 경우 \(x,y\)가 살고 있는 체를 바꿔가면서 생각할 수 있다. 그러니까, 타원곡선의 방정식을 만족하는 모든 실수의 쌍 \((x,y)\)을 생각하기도 하고, 모든 유리수 쌍 \((x,y)\)를 생각하기도 한다. 우리가 고려하고 있는 \(a,b\)가 정수이므로 이들을 유한체 \(\mathbb{F}_p\)의 원소로 생각해, 같은 유한체 원소의 쌍 \((x,y)\)들의 모임으로서의 타원곡선을 생각할 수도 있다. 방정식이 같아 보여도 다루고 있는 체가 달라질 수 있으므로, 수학자들은 ‘실수체 위에서의 타원곡선’, ‘유리수체 위에서의 타원곡선’, ‘유한체 위에서의 타원곡선’과 같은 말을 사용한다.
특별히, 정수론에서는 타원곡선의 모든 유리수해를 찾는 문제가 중요하게 다뤄진다. 이에 대한 질문을 따라가다 보면 현대수학의 매우 심오한 다양한 주제들을 만날 수 있다. 한 예로, 버치-스위너턴다이어 추측은 타원곡선의 유리수해의 개수와 유한체에서의 해의 개수 사이에 있는 놀라운 관계에 대한 수학의 중요한 미해결 문제이다. 유리수체 위의 타원곡선이 갖는 보형성은 ‘페르마의 마지막 정리’를 해결하는 데 결정적으로 사용되기도 하였다. 이에 관련된 이야기는 호라이즌의 글 ‘2018년 아벨상 수상자 로버트 랭글랜즈’에서도 다뤄진 바 있다. (https://horizon.kias.re.kr/6772/)
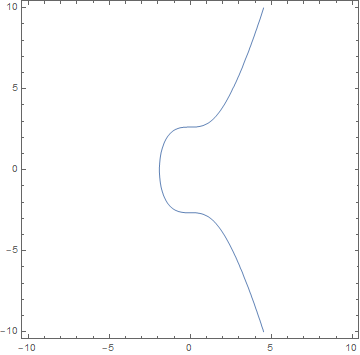
비트코인과 관련된 타원곡선의 방정식 \(y^2 = x^3 + 7\)의 실수해는, 좌표평면에서 다음과 같은 형태의 곡선으로 나타난다.[그림1] 이 타원곡선에 대한 각종 수학적 데이터는 이 링크에서 확인할 수 있다. (https://www.lmfdb.org/EllipticCurve/Q/21168/ce/2)
타원곡선에서의 덧셈
특정한 체에서 타원곡선의 방정식을 만족하는 해를 모아놓고 생각하면, 흥미로운 작업이 하나 가능해진다. 그것은 타원곡선의 두 점이 주어져 있을 때, 이 두 점을 이용해 타원곡선의 또 다른 점을 찾아내는 방법에 대한 것이다. 타원곡선의 모든 유리수해를 찾아내는 문제가 중요하다면, 이미 찾은 두 점을 이용해서 또 다른 점을 찾아내는 방법은 매우 유용한 것일 수 있다. 두 개를 찾으면, 하나를 더 찾을 수 있는데 사용하지 않을 이유가 없지 않은가?
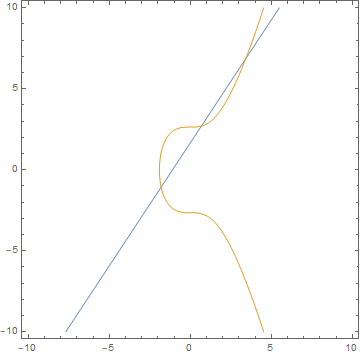
타원곡선의 실수해에 대해 생각하면 이는 기하학적으로 이해할 수 있다. 좌표평면상에서 \(x\)-좌표가 서로 다른 두 점 \(P, Q\)를 지나는 직선을 생각하면, 이 직선은 타원곡선과 세 점 \(P,Q,R\)에서 만나게 된다.[그림2] 타원곡선 방정식의 오른쪽에 3차식이 등장한다는 사실이 여기서 중요하다. 즉, \(P=(x_P, y_P)\), \(Q=(x_Q, y_Q)\)이고 \(x_P\neq x_Q\)인 경우라면, \(R=(x_R,y_R)\)은 다음과 같은 공식으로 표현된다:
\(\begin{align}s &= \frac{y_P – y_Q}{x_P – x_Q}\\x_R &= s^2 – x_P – x_Q\\y_R &= y_P + s(x_R – x_P)\end{align}\)
만약에 \(P\)와 \(Q\)가 같은 점이라면, 이때는 \(P=(x_P, y_P)\)를 지나는 접선이 타원곡선과 만나는 점을 이용하여 새로운 점 \(R\)을 찾을 수 있다. 이 경우, \(R=(x_R,y_R)\)은 다음과 같다:
\(\begin{align}s &= \frac{3{x_P}^2 + a}{2y_P}\\x_R &= s^2 – 2x_P\\y_R &= y_P + s(x_R – x_P).\end{align}\)
마지막으로, \(P\)와 \(Q\)의 \(x\)-좌표는 같지만 \(y\)-좌표의 부호만 다른 경우라면, \(P\)와 \(Q\)를 지나는 직선은 \(y\)축과 평행하게 되어 타원곡선과 두 점에서만 만나게 된다. 이 예외적인 상황은 타원곡선의 먼 곳에 어떤 가상의 점 \(\mathcal{O}\)이 하나 더 있는 것으로 생각해 개선할 수 있다. 그러면 이 직선도 역시 타원곡선과 \(P, Q, R=\mathcal{O}\)이라는 세 점에서 만난다고 말할 수 있다. 약간 억지스럽게 들릴 수도 있지만, 처음부터 타원곡선을 사영공간이라는 곳에 집어넣어 다루는 방식을 취하면 수학적으로 훨씬 자연스럽고 우아하게 이야기를 전개할 수 있다.
이렇게 알고 있는 두 점으로부터 새로운 점을 얻는 방법은, 마치 타원곡선 위에 있는 점들 사이의 일종의 연산처럼 보인다. 위에서처럼 두 점 \(P,Q\)로부터 \(R\)을 얻는 상황을 새로운 연산 기호 \(\circ\)를 도입해 \(P \circ Q = R\)이라고 표현해 보자. 그런데 이렇게 만들어진 연산에는 하나의 문제점이 있는데, 바로 결합법칙을 만족하지 않는다는 것이다. 즉,
\((x \circ y)\circ z = x \circ (y\circ z)\)
와 같은 식이 성립하지 않는다.
이 상황은 비교적 단순한 방식으로 개선할 수 있다. 점 \(R=(x_R,y_R)\)의 \(y\)-좌표의 부호만을 바꾸어 얻어지는 점을 \(-R=(x_R,-y_R)\)로 쓰자. 이제 위에서처럼 타원곡선의 두 점 \(P,Q\)로부터 새로운 점 \(R\)을 얻는 상황을 \(P+Q = -R\)라는 기호로 표현하면, 이 때의 연산 ‘+’은 결합법칙을 만족하게 된다. 이런 방향에서 생각을 계속 진전시키면, 가상의 점 \(\mathcal{O}\)는 덧셈에서 마치 0과 같은 역할을 하고 있음을 깨닫게 된다. 그리고 \(R+(-R)= \mathcal{O}\)과 같은 등식이 성립하는 것으로 생각할 수 있다. 두 점의 순서를 바꿔서 \(Q+P\)를 생각한다고 해도, \(P,Q,R\) 세 점이 한 직선 위에 있다는 사실에는 변함이 없으므로, 이 연산은 \(P+Q=Q+P\)와 같은 성질도 가지고 있다.
정리하자면, 타원곡선의 방정식을 만족하는 모든 실수해와 가상의 점 \(\mathcal{O}\)으로 이루어진 집합에는 덧셈과 유사한 성질을 갖는 연산을 정의할 수 있다. 이를 수학자들은 ‘실수체 위의 타원곡선에는 가환군 구조가 존재한다’고 말한다.
타원곡선에서의 덧셈과 관련된 위의 공식을 잘 들여다보면, \(x_R\)과 \(y_R\)은 \(x_P, y_P, x_Q, y_Q\)로부터 사칙연산만을 이용해 표현된다는 것을 알 수 있다. 이 공식들은 그림의 도움을 받아 유도되었지만, 사실은 그림이 없어도 본질적으로 대수적인 작업만을 이용해 유도되는 것이다. 부처님 말씀처럼 강을 건넜으면 배를 버려야 언덕에 오를 수 있다. 그림이 없이 실수체가 아닌 다른 체에 대해 생각하더라도 우리는 ‘유리수체 위의 타원곡선에는 가환군 구조가 존재한다’, ‘유한체 위의 타원곡선에는 가환군 구조가 존재한다’와 같은 결론을 내릴 수 있다. 덧셈에 대한 공식도 그대로 성립한다.
다음 이야기로 넘어가기 전에 유한체 \(\mathbb{F}_5\) 위에서 타원곡선 \(y^2=x^3+1\)의 예를 보자. 이 경우, \(\mathcal{O}\)를 포함하여 다음과 같은 여섯개의 타원곡선 상의 점이 존재한다:
\(\mathcal{O}, (0,1), (0,4), (2,2), (2,3), (4,0).\)
이 점들 사이의 덧셈은 다음 표로 주어진다:
\(\begin{array}{c|cccccc}+ & \mathcal{O} & (0,1) & (0,4) & (2,2) & (2,3) & (4,0) \\\hline\mathcal{O} & \mathcal{O} & (0,1) & (0,4) & (2,2) & (2,3) & (4,0)\\(0,1) & (0,1) & (0,4) & \mathcal{O} & (2,3) & (4,0) & (2,2) \\(0,4) & (0,4) & \mathcal{O} & (0,1) & (4,0) & (2,2) & (2,3) \\(2,2) & (2,2) & (2,3) & (4,0) & (0,4) & \mathcal{O} & (0,1) \\(2,3) & (2,3) & (4,0) & (2,2) & \mathcal{O} & (0,1) & (0,4) \\(4,0) & (4,0) & (2,2) & (2,3) & (0,1) & (0,4) & \mathcal{O} \\\end{array}\)
비트코인의 타원곡선과 비트코인 주소
이제 비트코인의 타원곡선에 대해 이야기할 준비가 되었다. 이제 소수 \(p=2^{256}-2^{32}-977\)를 고정한다. 비트코인 시스템은 유한체 \(\mathbb{F}_p\)위에서 정의된 타원곡선 \(y^2 = x^3+7\)을 사용한다. 이 타원곡선은 secp256k1라고 불린다.[3]
점 \(G=(x_1,y_1)\)
\(x_1 = 55066263022277343669578718895168534326250603453777594175500187360389116729240,\\y_1 = 32670510020758816978083085130507043184471273380659243275938904335757337482424\)
는 이 타원곡선 상에 놓여 있다. 이 사실은 컴퓨터를 활용하여 \(x_1^3+7\)과 \(y_1^2\)를 각각 \(p\)로 나눈 나머지가 같음을 확인하여 알 수 있다.
타원곡선의 점들끼리는 덧셈을 할 수 있으므로, 임의의 자연수 \(k\)에 대하여 \(G\)를 \(k\)번 더해서 얻어지는 점
\(kG = \overbrace{G+\dots+G}^{k}\)
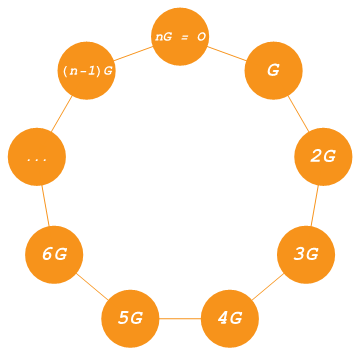
도 역시 타원곡선 위에 놓여있다. 이런 식으로 \(G,2G,3G,\dots\)와 같이 타원곡선 상의 다른 점을 얻을 수 있다. 이때, \(k\)를 키워나가다 보면 언젠가는 \(kG=\mathcal{O}\)가 되는 경우가 나타나는데, 이런 일은 \(k\)가
\(n=115792089237316195423570985008687907852837564279074904382605163141518161494337\)
일 때 처음으로 일어난다. 그 이후에 \(k\)의 값을 키우면 이제 \(G, 2G,\dots\)가 다시 등장한다.[그림3] 이렇듯 \(G\)의 반복적인 덧셈으로 타원곡선의 점 \(n\)개를 얻을 수 있는데, 이들이 모두 다르다는 것은 군론에 의해 보장된다.
글의 처음에서처럼 이제 1부터 \(n-1\) 사이의 자연수 \(k\)를 하나 선택했다고 하자. 그러면 타원곡선의 점
\(kG = (x_k, y_k)\)
는 컴퓨터를 이용하여 쉽게 계산할 수 있다. 암호학적으로 중요한 사실은 \((x_k, y_k)\)를 알고 있다고 해도, 거꾸로 \(k\)를 알아내는 것은 계산의 측면에서 굉장히 어려운 문제라는 것이다. 이를 이산 로그 문제라고 부른다. 타원곡선 암호학에서는 \(k\)를 비밀키, \((x_k, y_k)\)를 공개키라고 부른다. 공개키는 비밀키에서 쉽게 유도되지만, 공개키를 안다고 비밀키를 알아낼 수는 없다.
이제 비트코인 계좌번호, 즉 주소를 얻기 위해서는 공개키 \(x_k, y_k\)를 16진법으로 표현하고 이를 문자열로 생각한다. 그다음 정해진 약속에 따라 특정한 문자열을 더하고 SHA-256, RIPEMD-160와 같은 해시함수를 적용하는 과정을 반복적으로 거친다. 해시함수는 임의의 길이를 갖는 문자열을 입력받아 고정된 길이의 출력을 주는 컴퓨터 과학의 개념이다. 출력값으로부터 입력값을 찾는 것은 거의 불가능하기에, 비트코인 주소를 안다고 해도 공개키를 알 수는 없다. 비밀키에서 공개키, 공개키에서 주소로의 변환이 모두 비가역적이므로, 비밀키를 더 숨겨주는 효과가 생긴다.
현재 사용되고 있는 비트코인 주소의 형식에는 여러 가지가 있는데, 각각 약간씩 변형된 규칙이 적용된다. 다음과 같은 비트코인 주소들은 1을 비밀키로 갖는다:
- 1EHNa6Q4Jz2uvNExL497mE43ikXhwF6kZm (P2PKH 주소)
- 3JvL6Ymt8MVWiCNHC7oWU6nLeHNJKLZGLN (P2SH 주소)
- bc1qw508d6qejxtdg4y5r3zarvary0c5xw7kv8f3t4 (P2WPKH 주소)
이 주소의 비밀키는 모두가 알고 있으므로, 여기로 보내진 비트코인은 먼저 자기 주소로 가져가는 사람이 주인이다.
비밀키를 보관하고, 그로부터 주소를 생성해 주는 작업을 해주는 소프트웨어를 지갑이라고 부른다. 지갑에 들어있는 것은 비트코인이 아니라 비밀키일 뿐이다. 현실에서 일반 사용자가 타원곡선을 직접 다룰 필요는 전혀 없지만, 그들이 사용하고 있는 지갑 소프트웨어는 타원곡선의 계산을 수행해야만 한다. 주소를 생성하는 절차를 직접 실행하는 데 관심이 있는 사람들은, 이 링크에서 파이썬 코드를 살펴볼 수 있다.
(https://github.com/chlee-0/btc_native_segwit_address)
요약하면, 비밀키가 \(k\)인 비트코인 주소는 타원곡선의 점 \(kG\)의 좌표에 해시함수를 적용하여 얻어진다.
타원곡선 디지털서명 알고리듬
이렇게 해서 큰 숫자인 비밀키를 가지고 있고, 그로부터 비트코인 주소도 만들었다고 하자. 이렇게 스스로 만든 계좌를 가지고 있다고 해도, 어디에 로그인을 할 수 있는 것도 아니고 도대체 무엇을 할 수 있다는 것일까?
앞에서 나는 내가 생성한 비트코인의 주소를 언급했다. 그런데 이것이 정말로 내가 만든 것인지, 다른 사람의 것을 그냥 가져온 것인지 어떻게 알 수 있을까? 물론 주소에 대한 비밀키를 알려주면, 누구나 납득시킬 수 있다. 비밀키에서부터 같은 주소가 만들어지는지는 쉽게 확인할 수 있는 것이기 때문이다. 그러나 비밀키를 알려주지 않고도 내가 비밀키를 가지고 있다는 사실을 모든 사람이 믿게 만들 방법이 있을까?
이 문제를 해결해 주는 것이 바로 타원곡선 디지털서명 알고리듬이다. 타원곡선은 단지 비트코인의 주소 만드는 과정을 어렵게 만들기 위해서 사용된 것이 아니다. 디지털서명은 은행과 같은 중재자가 없는 환경에서, 비밀키를 가진 사람이 비밀키를 드러내지 않고서도 실제로 그것을 가지고 있음을 증명할 수 있는 수단을 제공해 준다. 그리고 이것이 새로운 형태의 거래를 가능하게 한다. 다음 글에서는 이 마법같이 들리는 타원곡선 디지털서명 알고리듬과 타원곡선의 암호학에 대한 이야기를 좀 더 소개하고자 한다.
참고문헌
- Serge Lang. Elliptic curves: Diophantine analysis. Springer-Verlag. 1978.
- 펠릭스 클라인. 19세기 수학의 발전에 대한 강의. 한경혜 옮김. 나남. 2012.
- Standards for Efficient Cryptography Group. SEC 2: Recommended Elliptic Curve Domain Parameteres, Version 2.0. 2010. https://www.secg.org/sec2-v2.pdf