[8월의 퍼즐 해설] 체스판 색칠하기

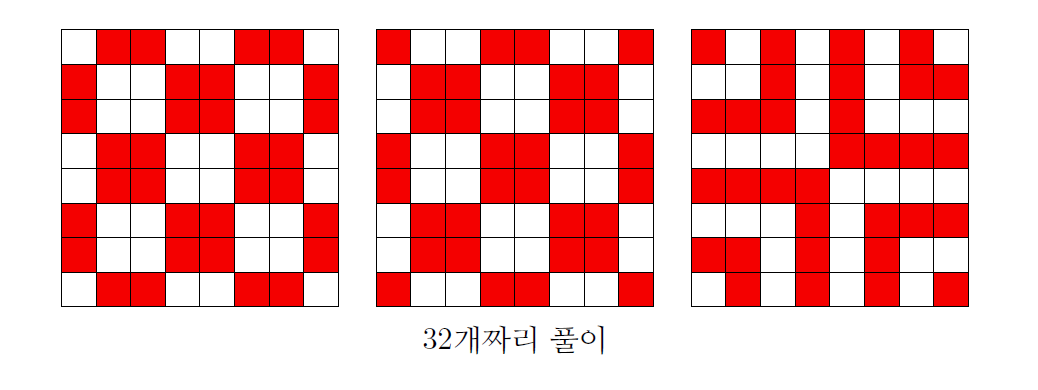
다음과 같이 대칭성 있는 32개짜리 답안을 제시한 분이 많았다. 이렇게 아름다운 풀이가 정답이 아닐 리가 없어 보이지만, 이보다 더 적은 칸을 칠하는 답이 존재한다.

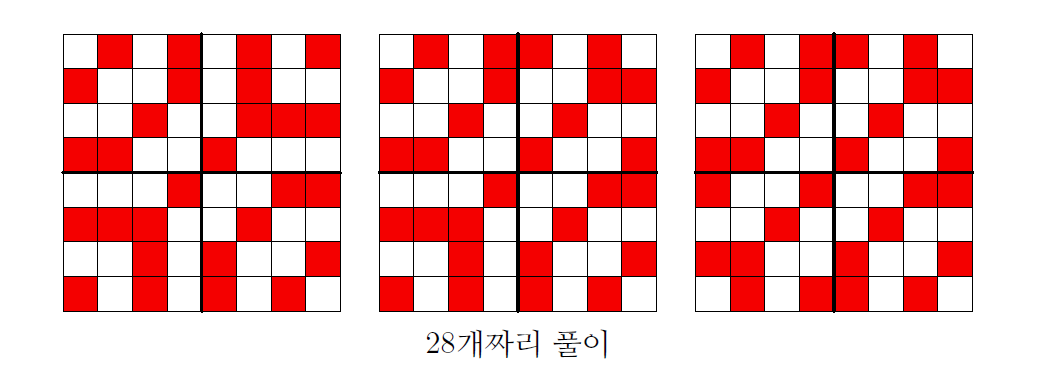
정답은 28개의 칸을 칠하는 것으로, 다음과 같이 세 종류가 가능하다. 체스판을 4등분하여 생각하면, 제2사분면과 제4사분면은 모두 똑같이 생겼고, 제1사분면과 제3사분면은 두 종류의 패턴을 바꾸어 가며 채웠음을 알 수 있다. 각 사분면은 7개의 칸이 색칠되어 있다. \(4 \times 4\) 격자에서 8개보다 적게 칸을 채운다고 생각하면 어렵지 않게 풀이를 발견할 수 있다.

체스판의 격자를 늘리면 어떻게 될까? \(8 \times 8\) 대신 \(9 \times 9\)를 생각하면, 이때는 뒤집거나 돌리는 것을 하나로 생각할 때 다음과 같은 35개짜리 답이 유일하게 존재한다.

다음은 8월의 정답자로 선정된 김일희님의 해설입니다.

흰 타일의 집합을 A, 붉은 타일의 집합을 B라고 하고, A 와 B 사이에 두 타일이 인접할 경우 edge 를 연결하는 이분그래프를 그려보자.
이 이분그래프의 edge의 갯수를 세는 방법으로 A에 있는 각 점에 연결되어 있는 edge의 갯수를 더하는 방법과 B에 있는 각 점에 연결되어 있는 edge의 갯수를 더하는 방법. 두 가지가 있다.
전자의 방법으로 갯수를 세면 조건에 의해 정확히 2|A| 가 나오고, 후자의 방법으로 센 결과는 4|B|보다 작거나 같다.
따라서 2|A| ≤ 4|B| 이고, |A| + |B| = 64 이므로 두 식을 이용하면, 3|B| ≥ 64. 즉, 빨간 타일의 갯수는 적어도 22 이상이어야 함을 쉽게 알 수 있다.

만약 전체 체스판이 아주 크다면, 혹은 무한한 체스판이라면, |B| 가 전체 타일 갯수의 1/3 이상이라는 이 부등식이 매우 타이트한 부등식이 된다.
왜냐하면, 대각선으로 번갈아가며 두 줄을 흰색, 한 줄을 빨간색으로 칠하면 조건을 만족하면서 빨간 타일이 전체의 1/3 가량 되도록 할 수 있기 때문이다. 하지만 체스판이 작은 사이즈이면, 바운더리 부근에서 조건을 만족하기 위해 빨간타일을 좀 더 써야하기 때문에 실제로는 1/3 보다 더 사용해야 한다.

위에서 edge 갯수의 상한을 4|B| 라고 했는데, 노력을 조금 더 기울이면 상한을 조금 더 낮추어 |B|의 하한을 조금 더 높일 수 있다.
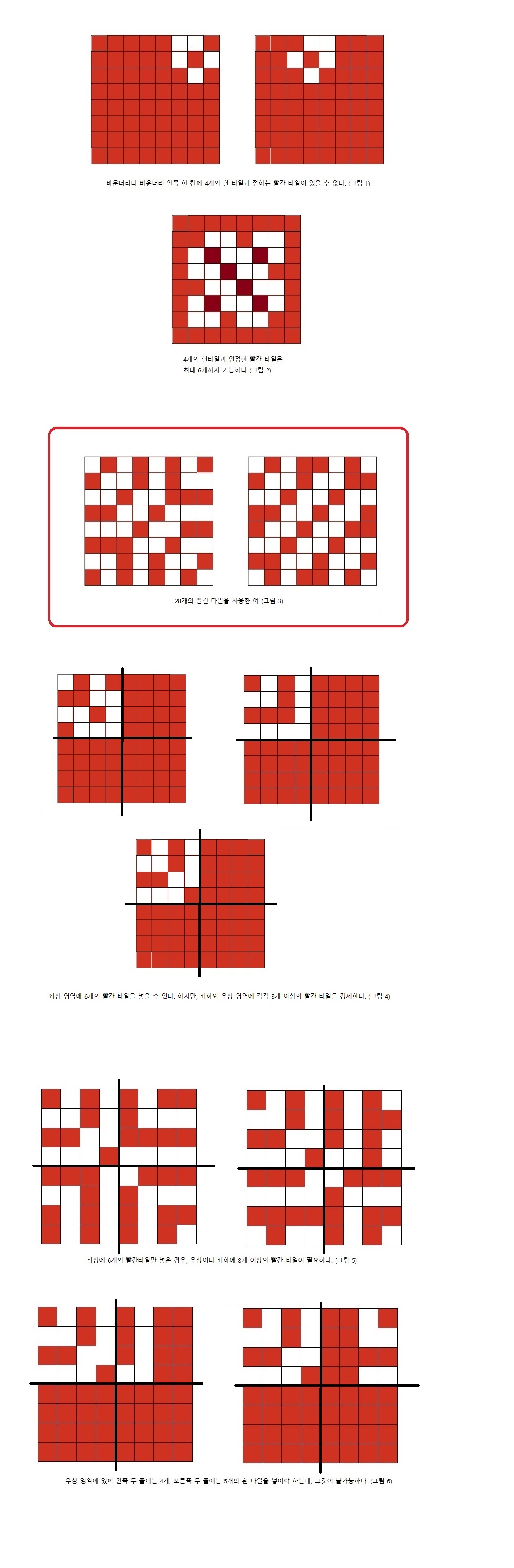
예를 들어, 바운더리나 바운더리 한칸 안쪽에는 흰 타일을 4개씩이나 접하는 빨간 타일이 존재할 수 없다는 사실을 보일 수 있다.
(바운더리에서는 총 접하는 타일자체가 4개보다 적으니 당연하고, 바운더리 한칸 안쪽에서는 그런 타일이 존재한다고 가정하면
그 빨간 타일에 접한 바운더리에 있는 흰 타일에 접한 또다른 흰 타일이 두개의 빨간타일을 접한다는 조건을 만족할 수 없다. 그림1 참고)

그리고, 흰색 타일을 4개 접하는 빨간 타일이 존재할 수 있는 정가운데 4*4 영역 안에서 그런 타일이 최대 6개까지 존재할 수 있다는 것도 어렵지 않게 생각할 수 있다. (그림2 참고 – 7개이상 있다고 하면, 두개의 2*4 영역 으로 나누었을 때, 적어도 한 영역에 4개의 흰 타일이 있어야 하는데, 각각 주변이 모두 빨간타일이어야 하니 지그재그로 교차하여 있으려고 하다보면, 빨간 타일 두개를 인접하는 것이 불가능하다.)
따라서, 4|B| 대신 4*6 + 3*(|B|-6) = 3|B| + 6으로 edge 갯수의 상한을 낮출 수 있다.
이를 이용하면, 2.5|B| +3 >= 64. 즉, 빨간 타일은 적어도 25 개 이상이어야 함을 알 수 있다.

그렇다면, 빨간타일 25개로 조건을 만족하며 칠할 수 있을까?
만약 그렇다면, 그것을 보여주는 것으로 문제가 끝나겠지만, 아쉽게도 25개만을 사용해서 조건을 만족하게 체스판을 칠하는 것은 불가능하다.
26개, 27개가 되어도 불가능하긴 마찬가지이다.
28개를 사용한다면, 비로소 그림 3의 두 예시처럼 조건을 만족하며 칠하는 것이 가능해진다.

이제, 27개 이하로 칠하는 것이 불가능함을 증명해보자.
모순을 위해, 27개 이하로 칠할 수 있다고 가정해보자.
그렇다면, 좌상, 좌하, 우상, 우하 총 4개의 4*4 영역 중 적어도 하나는 6개 이하의 빨간타일 (즉, 10개 이상의 흰타일)로 칠해져 있어야 한다. 일반성을 잃지 않고, 그 영역이 좌상영역이라고 해도 괜찮다.

그림 4에서와 같이 실제로 10개의 흰 타일로 칠해지는 그림이 가능하다.
하지만, 예들에서 보듯이 오른쪽과 아래쪽 경계에 흰 타일이 많이 포진되어 있어 우상영역과 좌하영역 경계에 많은 빨간 타일을 강제하고 있음을 알 수 있다. 먼저 흰 타일이 10개일 수 밖에 없고 (11개 이상은 불가능), 좌하 영역과 우상 영역의 경계에 3개이상의 빨간 타일을 강제할 수 밖에 없음을 보여보자.
(그리고 나서, 좌하와 우상에 빨간 타일이 많을 수 밖에 없다는 것을 통해 모순을 이끌어 내보자.)

위에서 설명한 이분그래프를 이 좌상 4*4 영역에만 한정해보고, 이 영역안에서 edge의 갯수를 세어 보자.
이제, 흰 타일입장에서 세는 edge 의 갯수는 2로 고정되어 있지 않다.
오른쪽과 아래쪽 경계에 있는 흰 타일에 대해서는 edge의 갯수가 1일 수도 있고, 가장 우하단 타일이 흰 타일일 경우 edge가 0개일수도 있다.
따라서 edge 의 갯수를 흰 타일 입장에서 세면, 2* (흰타일수) – (오른쪽과 아래쪽 경계에 있는 흰타일수) – 1 이상이 된다.

빨간 타일 입장에서 edge 를 세어보자. 먼저 4개의 흰 타일과 접하는 빨간 타일이 존재하는 경우부터 생각해보자.
그런 타일은 3번째 행 3번째 열에 있는 타일에만 존재할 수 있음을 쉽게 알 수 있다. (그림1에서 얘기한 바운더리 한칸 안쪽에 불가능한 논리 사용)
그리고, 전체 좌상 영역에 10개 이상의 흰타일이 존재해야 하는 (혹은 6개 이하의 빨간타일) 조건을 이용해 보면, 그림4의 첫번째 예가 유일한 경우임을 어렵지 않게 체크할 수 있다.
이 경우 우측 경계와 아래쪽 경계에 3개이상의 흰 타일이 포진되어 있고, 좌하와 우상 영역에 3개 이상의 빨간타일을 강제하고 있는 것이 참이다.

다음으로 좌상 영역에 흰타일을 4개씩이나 접하는 빨간 타일이 없는 경우를 생각해보자.
3개의 흰 타일과 인접한 빨간 타일은 몇개나 있을 수 있을까?
일단, 4*4 좌상 영역의 바운더리에 그런 타일이 있다고 가정해 보면, 전체 영역에 빨간 타일이 6개 이하라는 사실에 모순이 항상 발생함을 체크할 수 있다. 따라서 그런 타일은 내부 2*2 영역에만 존재할 수 있는데, 그 중 2개까지만 가능하여, 아래의 부등식이 성립한다.

2* (흰타일수) – (오른쪽과 아래쪽 경계에 있는 흰타일수 + 1) ≤ edge 갯수 ≤ 3 * 2 + 2 * (빨간타일수-2)

먼저, 좌상 영역에 총 흰 타일수가 11개 이상일 수는 없다. 22 – (7+1) ≤ 6 + 6 = 12 가 되어 모순이기 때문이다.
따라서, 빨간타일의 갯수는 정확히 6개 이고, 흰 타일의 수는 정확히 10개이며, 이 경우 부등식은
20 – (오른쪽과 아래쪽 경계에 있는 흰타일수의 갯수 + 1) ≤ 14
가 되어 오른쪽과 아래쪽 경계에 있는 흰타일수의 갯수가 5개 이상이라는 결론을 얻는다.
5개라고 하면 모든 부등호가 등호여야 하는데, 그럴 경우, 3개의 흰타일과 인접하는 빨간 타일 2개를 두면서, 오른쪽과 아래를 제외한 3*3 영역안에 흰 타일 5개를 둘 방법이 없으므로 불가능하다.
6개나 7개의 경우엔 실제 그림4의 2번째 3번째 예와 같이 가능하고, 이 경우에 우상이나 좌하영역의 경계에 각각 3개 이상의 빨간 타일을 강제하는 것이 모두 참이다.

이제, 우상과 좌하영역을 생각해보자.
좌상과 접하는 우상 영역의 왼쪽 열이나, 좌하영역의 위쪽 행을 각 영역의 오픈 경계라고 하자.

다음을 증명하자.
좌하나 우상의 영역처럼, 4*4 영역의 오픈 경계에 3개 이상의 빨간타일이어야 하는 조건이 붙으면,
그 영역 안에 적어도 8개 이상의 빨간 타일이 필요하다.

이것을 증명하면, 좌하, 우상 영역에서 각각 8개 이상의 빨간 타일이 필요하기 때문에,
총 6 + 8 + 8 + 6 = 28개 이상의 빨간 타일이 필요하게 되므로, 총 27개 이하로 칠한 가정에 모순이 발생하여 증명이 완성된다.
(실제로 좌상에 6개 이면서 총 28개인 construction 도 불가능해 보인다. 좌상에 6개이면 그림 5와 같이 6 + 8 + 8 + 9 = 31 혹은, 6 + 9 + 9 + 6 = 30개 정도가 최선으로 보이지만, 본 문제를 위해선 28개 이상을 증명하는 것으로 충분하기 때문에, 이 부분은 더 고려하지 않겠다.)

모순을 위해 오픈 경계에서 3개 이상이 빨간 타일인 조건을 달고, 우상 영역을 총 빨간타일 7개 이하로 칠할 수 있다고 가정해보자. (즉, 흰 타일이 9개 이상이어야 한다.)
오픈경계를 포함한 왼쪽 두 열에 들어갈 수 있는 흰 타일 갯수의 최대값은 5이다. 그런데, 5개가 다 들어가게 되면,
오른쪽에서 두번째 열이 모두 붉은 타일이어야 하고, 오른쪽 경계에 4개의 흰타일을 채우는 것이 불가능하다. (그림 6)
따라서, 오픈경계를 포함한 왼쪽 두 열에 들어갈 수 있는 흰 타일 갯수의 최대값은 4이다.
그리고, 오른쪽 두 열에 들어갈 수 있는 흰 타일 갯수의 최대값도 5임을 체크할 수 있다. (그림 6)
따라서, 총 9개가 들어가려면, 왼쪽 두 열에 정확히 4개, 오른쪽 두 열에 정확히 5개가 들어가야 한다.
그런데, 오른쪽 두 열에 5개가 들어가면, 왼쪽에서 두번째 열에 2개 이상 빨간 타일을 강제하게 되니,
왼쪽 두 열에 흰타일이 3개까지밖에 들어갈 수 없어 모순이 발생한다.

따라서, 우상 영역에 8개 이상, 같은 논리로 좌하 영역에 8개 이상의 빨간 타일이 필요하게 되므로, 전체적으로 28개 이상이 필요하게 된다.