10월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
10월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 김소윤님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
좌표평면의 원점에서 출발하여 x축 방향으로 1만큼 움직이고, 이어서 90도씩 꺾으며 2, 3, 4, . . . , n으로 움직인다면, 도착지 좌표의 x축 성분은 1±3±5±. . .가 되어야 하고, y축 성분은 ±2 ± 4 ± 6 ± . . .가 되어야 한다. 마지막에 y축을 따라 움직여 출발 지점으로 도착해야 하므로, n은 짝수라야 한다.
그러면 n = 2k라 할 때 x축 방향의 성분은 1 ± 3 ± 5 ± · · · ± (2k − 1)이 되고, 여기서 −를 모두 +로 바꾸면 홀수를 두 번 더한 셈이므로 1 + 3 + 5 + · · · + (2k − 1) = (2k − 1)k가 짝수가 되어야 한다. 따라서 k = 2ℓ이라 하자.
이제 세로 방향의 움직임을 나타내는 ±2 ± 4 ± 6 ± · · · ± n에서 −를 모두 +로 바꾸면 짝수를 두 번 더한 셈이므로, 2 + 4 + 6 + · · · + n이 4의 배수가 되어야 한다. 그러면
2 + 4 + 6 + · · · + 2k = 2(1 + 2 + 3 + · · · + k) = k(k + 1) = 2ℓ(2ℓ + 1)
이 4의 배수가 되는 경우는 ℓ이 짝수일 때이므로, 결국 n = 2k = 4ℓ은 8의 배수가 되어야 함을 알 수 있다.
실제로 1 ± 3 ± 5 ± 7 = 0이면서 ±2 ± 4 ± 6 ± 8 = 0인 경우를 찾아보면
1 − 3 − 5 + 7 = 0, 2 − 4 − 6 + 8 = 0
이므로 다음과 같은 그림을 그릴 수 있다.
이와 같은 도형을 처음 생각한 사람은 리 샐로스Lee Sallows로 그는 이 도형에 골리곤golygon이라는 이름을 붙였다.
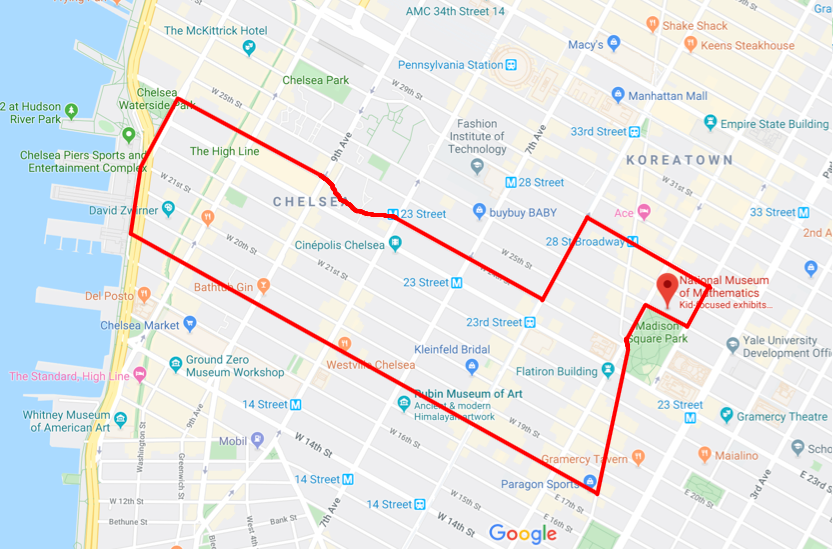
문제의 상황에서 미국 뉴욕 맨하탄의 MoMath 부근에서 도로를 따라 골리곤을 그릴 수 있다고 했는데, 약간 억지스러운 부분이 있기는 하지만, 다음과 같이 차례대로 한 블록, 두 블록, …, 여덟 블록을 움직여 제자리로 돌아올 수 있다.
다음은 10월의 정답자로 선정된 김소윤님의 해설입니다.