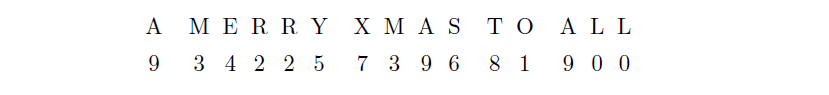12월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
12월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 남수연님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
이 문제는 Charles W. Tirgg의 책 Mathematical Quickies에서 발췌하였다.
A MERRY XMAS TO ALL의 모든 단어가 제곱수이므로, A로 가능한 값은 1, 4, 9이다. 이제 ALL을 생각해 보면, 제곱수가 되는 경우는 100, 400, 900, 144의 네 가지가 가능하다. 네 경우 모두 각 자리 숫자들의 합이 제곱수가 된다.
XMAS를 생각해 보면, 1296, 1849, 2916, 3249, 4096, 5041, 6241, 7396, 8649, 9216의 열 가지가 가능하고, 이 가운데 각 자리 숫자의 합이 제곱수가 되는 것은 \(7+3+9+6=25\)인 7396뿐이다. 따라서 \(\mathrm{X}=7, \mathrm{M}=3, \mathrm{A}=9, \mathrm{S}=6\)이 된다. 그러면 A가 9이므로 L은 0이 된다.
한편, TO가 제곱수이면서 각 자리 숫자들의 합도 제곱수가 되는 경우를 구해 보면 36, 81의 두 가지가 가능한데, 6은 S에서 이미 쓰였으므로, \(\mathrm{T}=8, \mathrm{O}=1\)이다.
이제 남은 숫자는 2, 4, 5이고 남은 단어는 MERRY=3ERRY이므로, 네 숫자가 모두 다 쓰이고 R에 해당하는 숫자는 두 번 쓰이게 된다. 그러면 \(\mathrm{M}+\mathrm{E}+\mathrm{R}+\mathrm{R}+\mathrm{Y} = 3+2+4+5+\mathrm{R} = 14+\mathrm{R}\)이므로 이 값이 제곱수가 되려면 R는 2일 수밖에 없다.
3E22Y가 제곱수가 되는 경우를 찾아보면 \(185^2 = 34225\)이므로, 이상의 결과를 정리하면
다음은 12월의 정답자로 선정된 남수연님의 해설입니다.