복잡한 것 단순하게 바라보기 [2]: 엄밀하지 않은 단순화의 위험

단순화의 조건

지난 1월호의 글 “복잡한 것 단순하게 바라보기[1]: 생화학 분야의 근의 공식, 미카엘리스-멘텐식”에서 준평형상태 근사^{Quasi-steady state approximation; QSSA}를 이용해 효소 반응을 묘사하는 4차원 멀티-타임스케일^{Multi-timescale}시스템을 1차원의 긴 타임 스케일 시스템으로 단순화하는 과정을 살펴보았다.

효소 반응 멀티-타임스케일 시스템은 빠르게 변화하는 변수들(\(C\), \(E\))와 느리게 변화하는 변수들(\(S\), \(P\))로 구성되어 있고 \(C\)와 \(E\)가 \(S\)와 \(P\)에 비해서 빠른 속도로 준평형상태(\(C(S)=\frac { { E }_{ T }S }{ S+{ K }_{ M } } ,\quad E(S)=\frac { { E }_{ T }{ K }_{ M } }{ S+{ K }_{ M } }\))에 도달한다. 이를 이용해서 아래 그림과 같이 빠른 변수들을 준평형 상태로 대체하여 제거함으로써 천천히 변화하는 변수들의 긴 타임스케일 변화를 묘사하는 단순화된 미분방정식을 유도할 수 있었다.

단순화된 미분방정식인 미카엘리스-멘텐^{Michaelis-Menten}식은 생명과학의 근의 공식이라고 할 수 있을 정도로 널리 사용되어 왔다. 이는 1903년 헨리^Henri와 1913년 미카엘리스^Michaelis와 멘텐^Menten의 논문[1]에서 처음 제안되었고 위와 같이 준평형상태를 이용해서 식을 유도한 것은 1925년 홀데인^Haldane이다.[2]

이후 1983년에 시겔^Segel과 슬램로드^Slemrod는 이 과정을 특이 섭동^{Singular perturbation} 이론을 이용해 수학적으로 엄밀히 연구하였다.[3] 그들은 이 연구에서, 미카엘리스-멘텐식이 \(C\)와 \(E\)가 \(S\)나 \(P\)에 비해 빠르게 준평형상태에 도달한다는 가정하에서만 가능한데 이는 항상 가능한 것은 아니며 특별한 경우에만 가능함을 증명하였다. 즉, 아래 조건과 같이 전체 효소 농도(\({ E }_{ T }=E+C\))가 전체 기질 농도(\({ S }_{ T }=S+C+P\))와 미카엘리스-멘텐 상수(\({ K }_{ M }=\frac { { k }_{ b } }{ { k }_{ f }+{ k }_{ cat } } \))의 합에 비해 훨씬 작을 경우에만 가능함을 밝혔다.

\(\frac { { E }_{ T } }{ { S }_{ T }+{ K }_{ M } } \ll 1\)

아래 그림에서 볼 수 있듯이 위 조건을 만족하는, 즉 효소 농도(\({ E }_{ T }\))가 낮을 때(왼쪽 그림)는, 단순한 미카엘리스-멘텐식의 해(점선)와 복잡한 원래 미분방정식의 해(실선)가 비슷하다. 즉 미카엘리스-멘텐식은 단순하지만 효소 반응의 생산물(\(P\)) 시간이 변함에 따라 어떻게 증가하는지 정확하게 예측함으로써 높은 가성비를 보인다. 하지만 효소 농도(\({ E }_{ T }\))가 높아지면 단순화된 미분방정식이 부정확해진다.(가운데/오른쪽 그림). 따라서 효소 농도가 높을 때는 미카엘리스-멘텐식을 사용하면 안 된다는 것이 자명하다. 게다가 효소 농도를 정확하게 측정할 수 없는 경우도 있어 미카엘리스-멘텐식을 사용해도 되는지 체크하는 것이 불가능할 때도 많다.

하지만 안타깝게도 이러한 미카엘리스-멘텐식에 대한 정확한 이해 없이, 수많은 논문에서 효소 농도가 높을 때에도 미카엘리스-멘텐식이 사용되고 있다.

더 넓은 범위에서 정확한 단순화

왜 효소 농도가 낮을 때에만 미카엘리스-멘텐식을 사용할 수 있을까? 효소 농도가 낮을 때는 \(C\)와 \(E\)가 \(S\)에 비해서 빨리 변화하지만 효소 농도가 높아지면 \(S\)와 비슷한 속도로 변화하거나 혹은 오히려 더 느려진다. 따라서 이 경우에는 \(C\)와 \(E\)가 빠르게 준평형 상태로 도달한다는 가정을 할 수 없다. 즉 단순화를 할 수 없다.

이 문제는 아주 간단한 치환으로 해결할 수 있다. 바로 \(S\)를 더 느린 변수로 치환함으로써 효소 농도에 상관없이 \(C\)와 \(E\)가 항상 빠른 변수가 되도록 하는 것이다. 즉 기존의 미분방정식에서 \(S\) 대신 더 느린 변수인 \(T=S+C\)라는 새로운 변수로 치환하면 원래 시스템과 동일한 미분방정식을 유도할 수 있다. \(T\)에 대한 미분방정식은 위의 \(S\)와 \(C\)미분방정식을 합하면 된다.

\(\frac { dT }{ dt } =-{ k }_{ cat }c\\ \frac { dE }{ dt } =-{ k }_{ f }E(T-C)+{ k }_{ b }c+{ k }_{ cat }c\\ \frac { dC }{ dt } ={ k }_{ f }E(T-C)-{ k }_{ b }c-{ k }_{ cat }c\\ \frac { dP }{ dt } ={ k }_{ cat }c\)

이 간단한 치환이 놀라운 변화를 가져온다. 기존 미분방정식을 단순화하려면 \(C\)가 \(S\)에 비해서 더 빠르게 준평형상태에 도달하는지가 관건이었는데 치환 후에는 \(S\) 대신 \(T\)와 비교하면 된다. \(T\)가 \(S\)에 비해서 더 느리게 변화하기 때문에 더 넓은 조건에서 그러할 것이라 예상할 수 있는데, 실제로 효소 농도와 상관없이 \(C\)는 \(T\)에 비해서 항상 더 빠르게 준평형 상태에 도달한다.[4] 느린 변수를 더 느린 변수로 치환한 덕분에 이제 아무런 제약 없이 미분방정식을 단순화할 수 있게 되었다.

준평형상태는 기존과 마찬가지로 \(\frac { dc }{ dt } =0\)\((i.e.\quad{ k }_{ f }({ E }_{ T }-C)(T-C)-{ k }_{ b }c-{ k }_{ cat }c=0\))을 풀어 아래와 같이 구할 수 있다. 다만 기존의 준평형 상태는 \(S\)에 의해서 결정되는 함수였다면 이제는 \(T\)에 의해서 결정되는 함수이다.

\(C(T)=\frac { { E }_{ T }{ +K }_{ M }+T-\sqrt { { ({ E }_{ T }{ +K }_{ M }+T) }^{ 2 }-4{ E }_{ T }T } }{ 2 }\)

그리고 \(E(T)={ E }_{ T }-C(T)\)가 된다. 중학교에서 배우는 2차 방정식 근의 공식을 이용해 구한 위 식을 이용해서 빠른 변수 \(C\)와 \(E\)를 제거하면 아래와 같이 새롭게 단순화된 미분방정식을 유도할 수 있다.

\(\frac { dT }{ dt } =-{ k }_{ cat }\frac { { E }_{ T }{ +K }_{ M }+T-\sqrt { { ({ E }_{ T }{ +K }_{ M }+T) }^{ 2 }-4{ E }_{ T }T } }{ 2 } \\ \frac { dP }{ dt } ={ k }_{ cat }\frac { { E }_{ T }{ +K }_{ M }+T-\sqrt { { ({ E }_{ T }{ +K }_{ M }+T) }^{ 2 }-4{ E }_{ T }T } }{ 2 } \)

전체 기질 농도 \({ S }_{ T }=T+P\)가 불변량임을 이용하면 \(T={ S }_{ T }-P\)이므로 변수 \(T\)를 제거하여 아래와 같이 더 단순화된 미분방정식을 구할 수 있다.

\(\frac { dP }{ dt } ={ k }_{ cat }\frac { { E }_{ T }{ +K }_{ M }+{ S }_{ T }-P-\sqrt { { ({ E }_{ T }{ +K }_{ M }+{ S }_{ T }-P) }^{ 2 }-4{ E }_{ T }({ S }_{ T }-P) } }{ 2 }\)

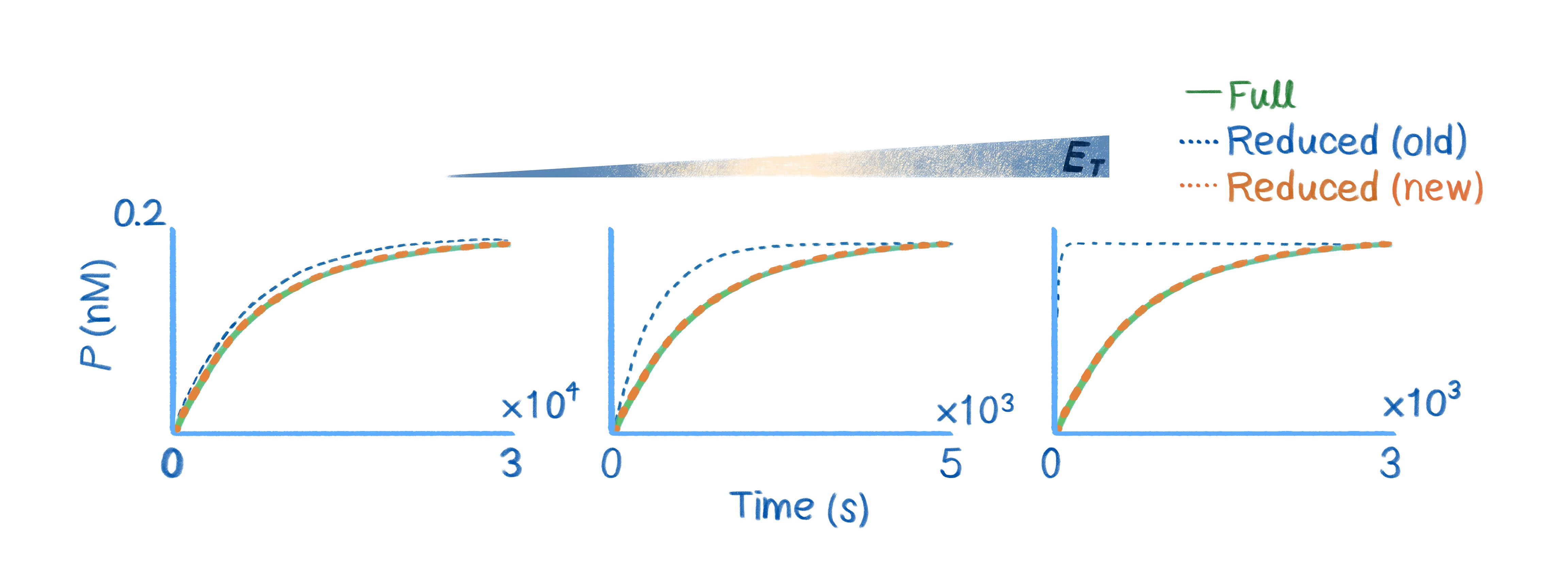
아래 그림에서 볼 수 있듯이 기존의 단순화된 미분방정식(파란 점선)과 달리 새로운 미분방정식의 해(빨간 점선)는 효소 농도와 상관없이 원래 미분방정식의 해(초록 실선)에 정확하게 근사함을 알 수 있다. 이 식은 미카엘리스-멘텐식만큼 단순해서 가성비도 좋고 미카엘리스-멘텐식과 달리 정확도 면에서도 흠잡을 데가 없다.

따라서 기존의 미카엘리스-멘텐식에 비해 이 식이 널리 사용되어야 할 것 같지만, 미카엘리스-멘텐식에 비해 덜 직관적이고 해석의 복잡함으로 인해 미카엘리스-멘텐식만큼 널리 사용되지는 않았다. 최근에야 이 새로운 식을 이용해서 효소들의 반응 속도 매개 변수들(\({ k }_{ cat }\), \({ K }_{ M }\))을 역으로 추정해내는 연구들이 진행되고 있다.[5]

위와 같이 변수 치환(\(T=S+C\))을 통해서 기존 시스템과 동일하지만 변수들 사이의 속도 차이를 극대화하여 더 넓은 범위에서 정확한 단순화 방법을  총합 준평형상태 근사^{Total Quasi-steady-state approximation}라고 한다. 하지만 시스템이 복잡해지면 어떤 변수들을 치환해야 하는지를 찾는 것은 복잡한 문제여서 이를 위한 일반적인 방법과 알고리즘이 존재하지 않아 이를 위한 연구가 여전히 진행중이다.[6]

멀티스케일 확률미분방정식의 단순화

지금까지 멀티스케일 생화학 반응을 묘사하는 상미분방정식 시스템을 단순화하는 것에 대해 살펴보았다. 그런데 실제 생화학반응은 확률적으로 일어나는 스토캐스틱^Stochastic 시스템이다. 즉, 실제로 실험을 통해서 생산물(\(P\))이 어떻게 증가하는지 측정하면 위에서 보았던 그래프처럼 부드럽게 증가하는 것이 아니라 들쭉날쭉할 것이다. 이러한 변동^Fluctuation을 묘사하기 위해서는 상미분방정식 대신 확률미분방정식^{Stochastic differential equation}을 사용해야 한다. 멀티스케일 상미분방정식을 단순화하는데 사용했던 것처럼 멀티스케일 확률미분방정식 역시 빠른 변수의 준평형상태를 이용해서 단순화할 수 있다.

다만 확률미분방정식의 준평상태는 천천히 변화하는 변수가 고정되어 있다고 가정했을 때 빠르게 변화하는 변수들의 “조건부 평균”이다. 따라서 빠르게 변화하는 변수들을 각각의 조건부 평균으로 치환하면 느리게 변화하는 변수들로만 구성되어 있는 단순화된 확률미분방정식을 구할 수 있다.

하지만 아주 특별한 경우에만 조건부 평균을 구할 수 있다. 예를 들어, 모든 반응이 선형이라서 조건부 평균을 구하는 것과 상미분방정식의 준평형 상태를 구하는 식이 동치가 되는 경우, 비선형적인 반응이 있는 경우에는 단순한 Birth-death 프로세스, Feed-forward 프로세스 등에서만 유도할 수 있다.[7]

이런 특별한 경우를 제외한 대부분의 경우에는 확률미분방정식의 준평형상태를 계산할 수 없기 때문에 이를 손쉽게 구할 수 있는 상미분방정식의 준평형상태로 대체해서 사용하는 방법(확률준평형근사, Stochastic QSSA)이 수백 편의 논문에서 사용되고 있다. 하지만 원래 확률 미분 방정식의 변동성을 단순화된 미분 방정식이 정확하게 근사하는 경우(위 그림)도 있고 그렇지 못한 경우(아래 그림)도 있다. 이렇게 경우에 따라 부정확 할 수 있지만, 이 방법을 사용하면 계산 속도가 적어도 수백 배는 빨라지기 때문에 많은 연구자들이 사용하고 있다. 이러한 방법의 정확도에 대한 연구는 최근에 들어서야 시작되었고 몇 가지 유명한 수리 모델에 대해서만 답을 알고 있다.[8][9][10]  따라서 일반적인 확률미분방정식의 준평형 상태를 계산하는 방법이나 혹은 이를 정확하게 근사하는 방법을 찾는 것은 수리 생물학 분야의 가장 중요한 문제 중 하나이다.

미카엘리스-멘텐식에 기반한 “상미분방정식”이 어느 조건에서 정확한지 시겔^Segel과 슬램로드^Slemrod가 엄밀하게 유도하기까지 약 90년이 걸렸다.[1][2][3] 미카엘리스-멘텐식에 기반한 “확률미분방정식”에 대한 답은 좀 더 일찍 알 수 있었으면 좋겠다.