2월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
2월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 곽욱탁님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
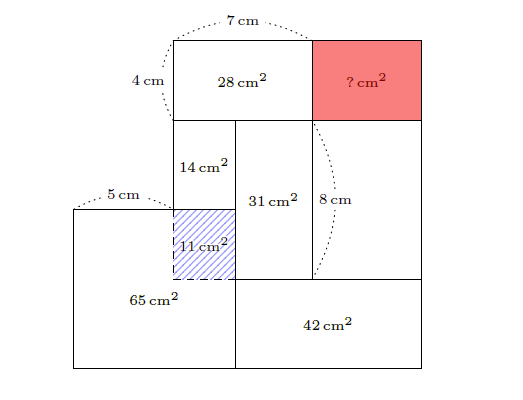
먼저 위쪽 넓이 \(28\,\mathrm{cm}^2\)인 직사각형의 가로는 \(7\,\mathrm{cm}^2\)이다. 이제 그림과 같이 왼쪽 아래 넓이 \(65\,\mathrm{cm}^2\)인 직사각형의 오른쪽 구석에 작은 직사각형을 하나 그린다. 그러면 빗금 친 부분의 널이는 \(7 \times 8 – 14 – 31 = 11\,(\mathrm{cm}^2)\)가 된다.
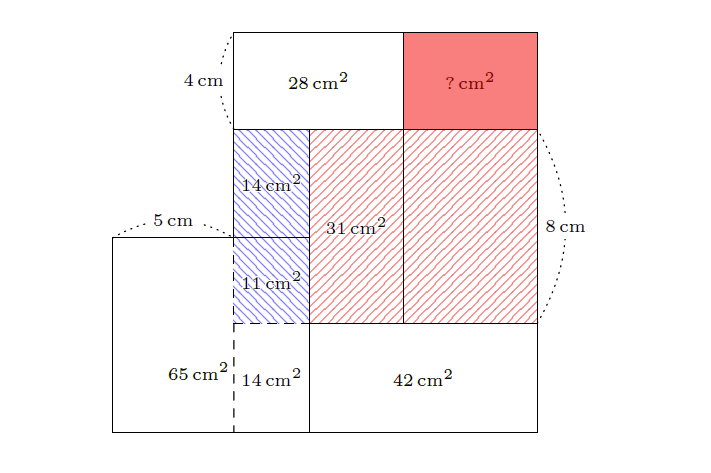
이번에는 넓이 \(14\,\mathrm{cm}^2\)인 직사각형과 넓이 \(11\,\mathrm{cm}^2\)인 직사각형의 왼쪽에 직사각형을 그리면, 빗금 친 부분의 넓이는 \(5 \times 8 + 14 + 11 = 65\,(\mathrm{cm}^2)\)가 된다. 그런데 이 넓이는 왼쪽 아래에 있던 원래 직사각형의 넓이와 같다.
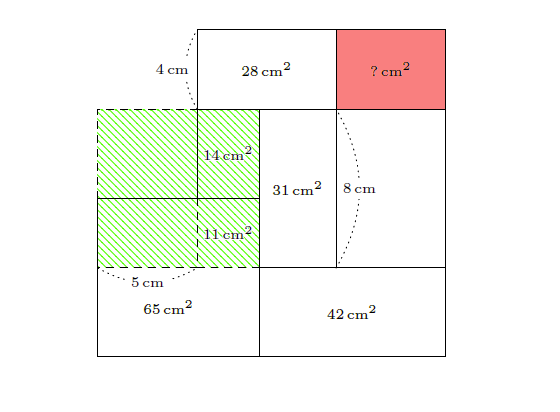따라서 아래 그림에서 빗금 친 직사각형의 넓이는 \(14\,\mathrm{cm}^2\)와 같다. 그러면 이 직사각형과 그 오른쪽 직사각형의 넓이의 비는 \(1:3\)이다.
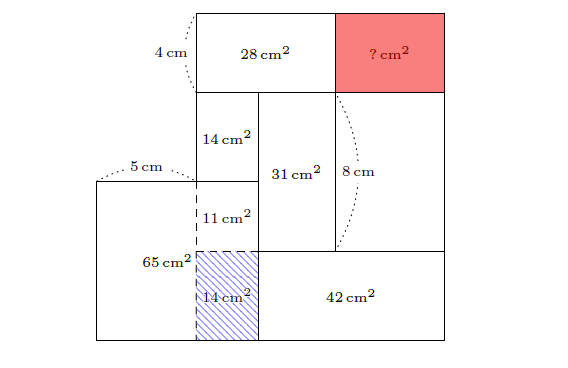
이제 아래 그림에서 빗금 친 두 영역의 넓이를 비교하면, 물음표로 표시된 직사각형 아래 큰 직사각형의 넓이는 \(3 \times (14+11)-31 = 44\,(\mathrm{cm}^2)\)가 된다. 아래위 두 직사각형의 높이가 각각 \(4\,\mathrm{cm}\)이고 \(8\,\mathrm{cm}\)이므로, 물음표로 표시된 직사각형의 넓이는 \(44\,\mathrm{cm}^2\)의 절반인 \(22\,\mathrm{cm}^2\)이다.
2020년 2월 문제이니 답이 22인 것은 당연하지 않은가?
다음은 2월의 정답자로 선정된 곽욱탁님의 해설입니다.
모처럼 아마추어도 풀수 있는 문제로군요.
