스트림스 게임으로 시작하는 강화학습 [1]

Hands-on Reinforcement Learning with the Streams Game [1]

딥러닝과 강화학습의 출현!

2010년대 중반은 기계학습의 지도학습분야에서 딥러닝^{deep learning}이 기존 알고리즘들의 성능을 압도하면서, 데이터 기반 함수 작성법에 대한 인기가 급부상하고 있는 즈음이었고, 많은 컴퓨터 공학자들이 새롭게 이를 공부하느라 분주하던 무렵이었다.[1]

그런 와중에 2016년 3월 딥마인드의 알파고가 이세돌 9단과의 5번기를 4대 1로 승리하는 믿을 수 없는 사건이 벌어졌다.[2] 바둑만큼은 인공지능의 도전을 받지 않을 마지막 성역 같은 곳이라고 생각했었는데 완전히 허를 찔린 기분이었다. 그때 알파고가 사용한 방법은 ‘강화학습^{reinforcement learning}’에 딥러닝을 접목한 ‘심층강화학습^{deep reinforcement learning}’이라는, 당시에는 내가 전혀 관심을 갖고 있지 않던 기법이었다.[3][4]

과거에는 엄두도 못 내던 엄청난 크기와 복잡도의 바둑 문제를 해결해버린 이 외계인 같은 알고리즘 앞에서, 내가 동경하던 ‘우아한 수학적 알고리즘’의 시대는 종말을 맞이한 것인가 하는 막연한 두려움이 앞섰다. 당장은 새로운 공부거리가 계속 늘어가는 것에 대한 부담도 커졌다. “이 새로운 함수 작성법들을 언제 다 배우고 마스터하지?”

절반은 호기심에서 나머지 절반은 첨단 연구 동향을 추적해야 하는 연구원의 소명으로, 결국 딥러닝과 더불어 강화학습도 함께 공부해 보기로 했다. 다만 좀 남다른 방식으로 접근해서 배워 보고 싶었다. 딥마인드가 해결한 아타리^ATARI 게임처럼 잘 알려진 게임을 다루기보다는 전혀 새로운 문제에 도전해 보고 싶었다. 그렇다고 바둑처럼 어마어마한 게임에 도전할 여력은 없었다. 연구소에서 맡은 일 외에 별도로 하는 일이라 시간이나 계산자원을 따로 할당하기도 쉽지 않은 터였다.

그러던 와중에 연구소의 자발적인 학습 동아리인 GTA^{Game Theory AOC, 게임이론 동호회}에서 심층강화학습 스터디를 시작하게 되었고, 이때 소개받은 ‘스트림스 게임’에 심층강화학습을 적용해 보면 좋겠다는 생각이 들었다.[5]

이번 연재글에서는 스트림스 게임, 그리고 이 게임을 스스로 플레이하는 함수, 즉 스트림스 게임 에이전트^{game agent}를 제작하는 방법을 소개하고자 한다. 먼저 1편에서는 스트림스 게임을 소개하고 전통적인 규칙·탐색기반 방법까지 설명한 뒤, 2편에서 심층강화학습과 이를 적용한 스트림스 게임 에이전트에 대해서 살펴볼 예정이다.

스트림스 게임이란?

스트림스 게임은 ‘오름차순 빙고게임’이라고 정의할 수 있다. ‘빙고’가 암시하듯이 이 게임의 가장 큰 매력은 간단한 규칙에 있다.[5] 초등학생 정도면 규칙 설명을 듣자마자 바로 플레이를 해볼 수 있을 것이다. 또한 여럿이 함께 모여 플레이가 가능한 소셜 게임이기도 하다.

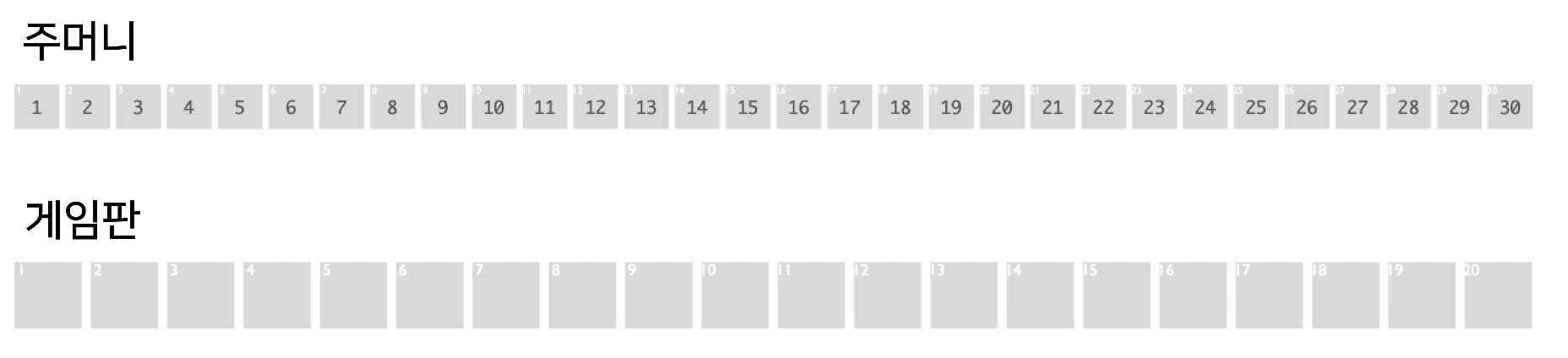
자, 규칙을 살펴보자. 스트림스 게임에는 말판과 말이 필요하다. 말판에는 20개의 빈 칸이 한 줄로 배열되어 있다. 말은 주머니에 들어 있는 1부터 30까지의 숫자들이다. 주머니에 반복되는 숫자들은 없다. 이 주머니에서 말을 하나씩 꺼내서 말판의 빈칸이라면 어디라도 배치하면 된다. 단, 최종적으로 20개의 칸에 말들이 모두 배치되었을 때 가장 긴 오름차순의 배열이 만들어지도록 하면 된다. 꺼낸 숫자는 주머니에 다시 넣지 않는다. (아래에서 이 기본 게임을 S20.30으로 부르기로 한다.)

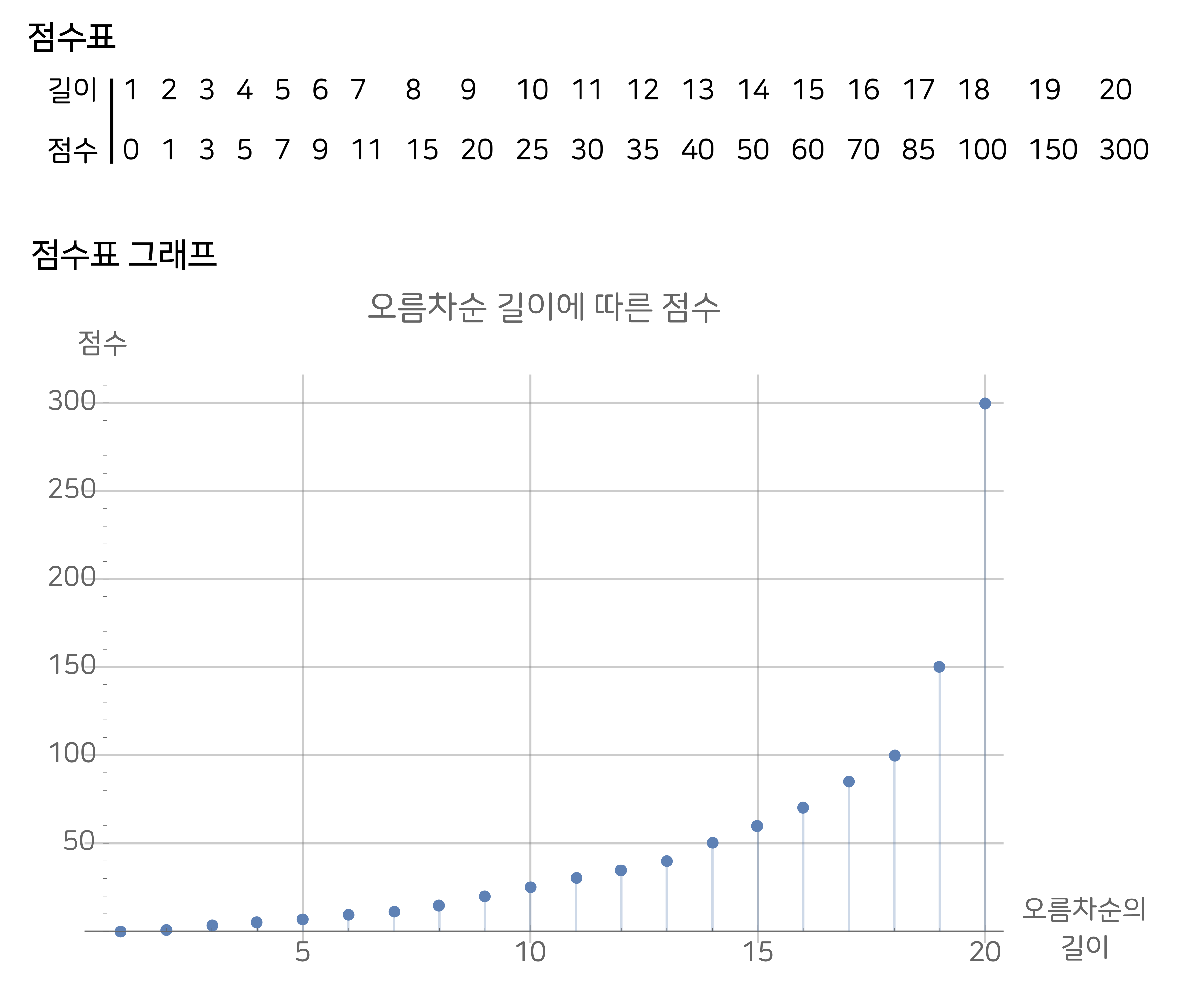
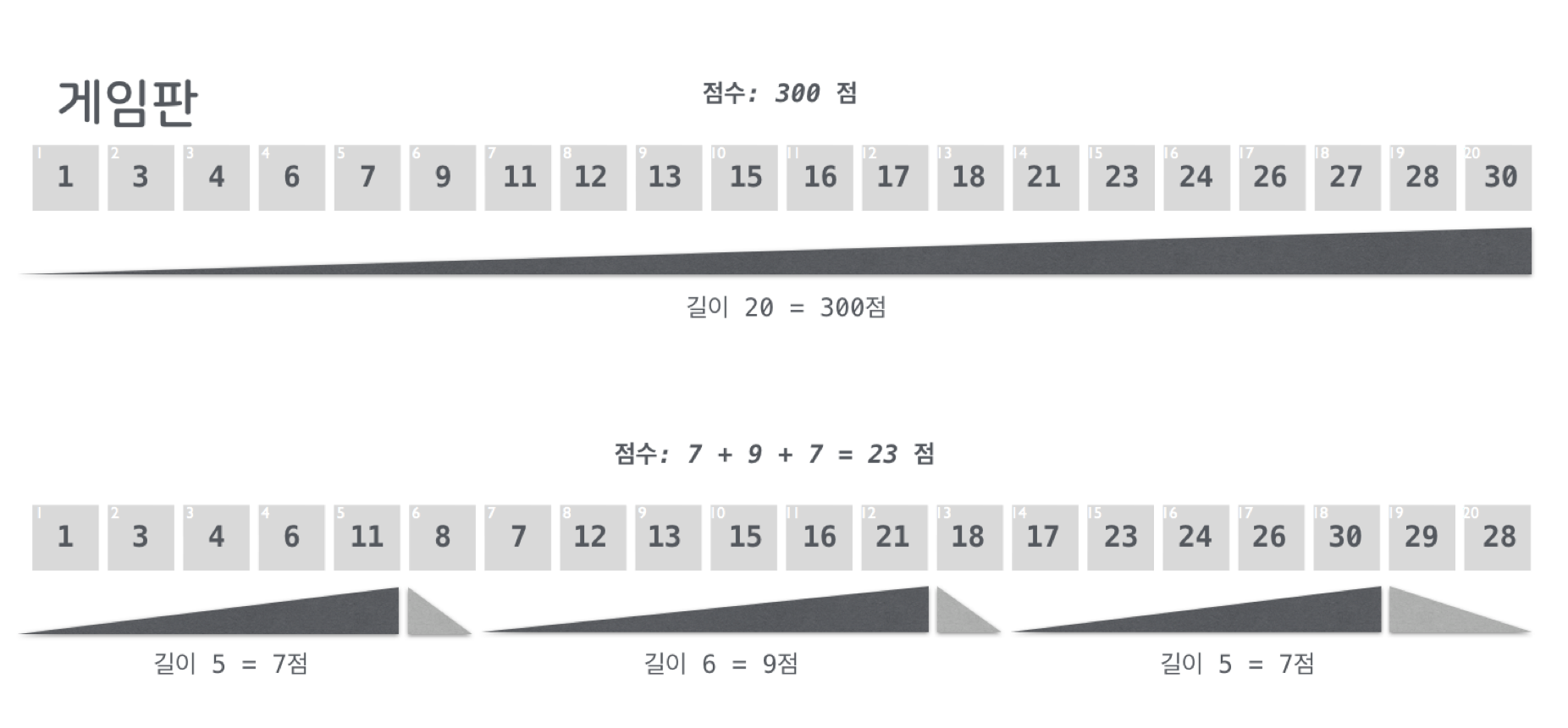
스트림스 게임의 점수는 차례로 꺼낸 (또는 불러 준) 스무 개의 숫자를 말판에 모두 채우고 나서, 오름차순 배열의 덩어리마다 점수를 구하고 이들을 모두 더하여 계산한다. 이때 점수는 오름차순 배열의 길이에 따라 기하급수적으로 증가한다. 즉, 길이가 한 칸이라도 더 긴 배열은 점수가 훨씬 높아진다.

아래 [그림3]은 채점의 예를 보여준다. 먼저 말판의 스무 칸이 모두 하나의 오름차순 배열이 된다면 최고점을 받는다. 하지만 두 번째 예처럼 세 개의 덩어리로 나눠진다면, 부분 점수 세 개를 각각 구하고 이를 더하면 된다. 중간에 끊어진 부분은 계산하지 않는다.

스트림스 게임의 다른 매력은 게임의 크기를 조정할 수 있다는 점이다.  예를 들어, S5.10 ‘미니’ 스트림스 게임은 1부터 10까지의 숫자 중에서 다섯 개의 숫자를 무작위로 하나씩 꺼내고, 그때마다 다섯 칸 길이의 말판에 오름차순의 배열이 되도록 채워 넣으면 된다. 이렇게 작은 규모의 게임을 만들 수 있으면 컴퓨터 알고리즘을 테스트할 때 무척 편리하다. (특히 강화학습처럼 시간이 오래 걸리는 알고리즘의 테스트에는 필수적이다!) 스트림스 게임을 처음 접하는 사람들도 S20.30을 본격적으로 풀어 보기 전에 S5.10이나 S10.20을 몸풀기로 풀어보면 도움이 많이 된다.

세 번째 매력은 게임의 우연성이다. 이는 스트림스 게임의 결정적인 재미요소이다. 말판에 넣어야 할 다음 숫자가 어떤 것이 나올지 모르기 때문에 말판의 현재 상황을 파악하며 미래의 위험을 함께 관리해야 하는 등의 세심한 전략이 필요하다. 따라서 스트림스 게임의 진정한 실력을 가늠하기 위해서는 여러 번의 서로 다른 플레이를 해서 그 점수들을 종합적으로 판단해야 한다. 단 한 번의 플레이로 참가자의 실력을 파악할 수는 없다. 따라서 스트림스 게임 에이전트를 제작해야 한다면 이러한 우연성에 의한 통계적 특성을 고려할 수 있어야 한다. 아래에서 실제 스트림스 게임을 플레이해 보며 게임의 특성을 몸소 느끼고 또 생각해 보자.

스트림스 게임을 해보자

스트림스 게임은 시중에서 보드게임 형태로 판매되고 있다.[5] 하지만 규칙만 알고 있으면 간단한 도구들로 혼자서도 손쉽게 플레이를 해볼 수 있다. 먼저 종이와 연필, 그리고 난수 생성기^{random number generator}를 준비하자. 난수 생성기는 웹이나 앱으로 쉽게 구할 수 있다. 종이에는 스트림스 말판이 칸으로 그려져 있으면 된다. 아래 [그림4]는 S5.10, S10.20, S20.30의 말판을 예로 보여준다. 말판 하단에는 점수표도 표시되어 있다. 이 표를 인쇄하고, 난수 생성기를 실행하며 나온 숫자를 오름차순을 만드는 것을 목표로 빈칸에 하나씩 적어나가면 된다. 난수 하나를 생성하고 이를 말판에 적고, 또다시 난수를 생성해 말판에 적는 과정을 반복하면 된다.

스트림스 게임의 전략에서 가장 중요한 것은, 현재의 말을 말판의 어느 곳에 배치할지 결정하는 것이다. 작은 숫자부터 차례로 말을 뽑는다는 보장이 없는데 말판의 왼쪽에서부터 차례로 말을 채워나간다면 고득점을 받을 수 있을까? 스트림스 게임 플레이의 매력은 현재의 말판, 새로 뽑은 말, 주머니 안의 남은 말들을 모두 고려하여 말판에서 오름차순을 만들어 내는 것이다. 자, 이제 스트림스 게임 플레이에 도전해 보자!

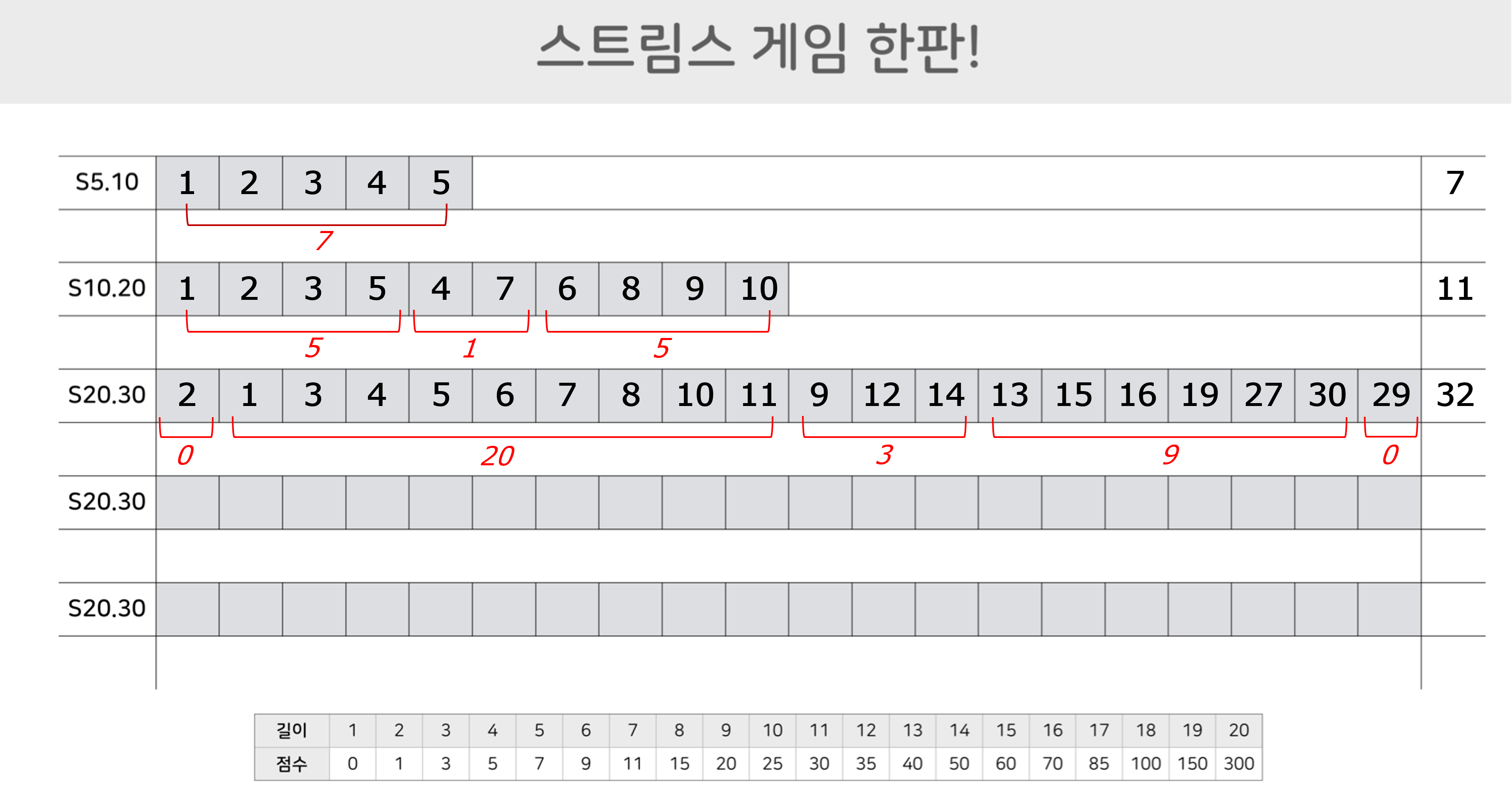
몸풀기 S5.10에서 본 게임 S10.20까지 각 게임이 끝나면 위에서 설명한 방식으로 채점을 해 본다. 아래 [그림5]는 S5.10, S10.20, S20.30에 대한 채점의 예를 보여 준다.

자, 독자들이 어느 정도 점수를 받았는지 궁금하다. 앞서 말했지만, 스트림스는 통계적 게임이기 때문에 한 두 번의 플레이로 여러분의 실력을 가늠할 수는 없다. 다만 앞으로 설명할 스트림스 게임 에이전트의 대략의 성능을 공개하자면, S5.10, S10.20, S20.30 게임에서 평균적으로 5.2점, 14.2점, 50점의 성능을 얻었다. 다음에는 강화학습 방법을 적용하기에 앞서 전통적인 방법인 규칙기반^rule-based과 탐색기반^search-based 방법으로 스트림스 게임 에이전트를 제작한 이야기를 들려 드리고자 한다.

스트림스 게임의 구현

본격적으로 스트림스 게임 에이전트를 구현하기 시작하던 2017년 무렵에는 심층강화학습에 대한 경험이 거의 없는 터였다. 그래서 먼저 평소에 선호하고 잘 아는 방법으로 스트림스 에이전트를 구현해 보고, 그 성능에 필적하는 심층강화학습 에이전트를 최종적으로 구현해 보는 것이 좋겠다고 생각하였다.

그리고 위에서 스트림스 게임을 직접 플레이해 본 분들이라면 느꼈겠지만, 사실 이 간단한 게임을 위해 첨단 “심층강화학습”까지 사용해야 하는지에 대한 의구심도 갖고 있었다. “기존의 ‘우아한 알고리즘’만으로는 스트림스 게임 에이전트를 만들 수 없는 것일까?”

규칙 기반 방법

모든 게임이 그러하지만, 스트림스 게임 역시 ‘매순간의 선택’들이 모여 성패를 결정한다. 매순간 판단해야 할 문제는 간단하다. “새로운 말을 현재 말판의 빈칸 어디에 넣어야 긴 오름차순을 만들어 높은 점수를 받게 될까?”

이에 대한 가장 간단한 구현 방법은 특정 조건을 만족하면 그에 해당하는 미리 정의된 행동을 선택하도록 하는 것이다. (보통 컴퓨터 코딩에서는 If-Then-Else 구문으로 이를 구현한다.) 예를 들어, “1이 들어 오면 말판의 맨 앞에 넣는다”도 규칙이 될 수 있다. 이 방법의 핵심은 가능한 많은 조건들을 찾아내고, 그에 대한 적합한 행동을 지정하는 것이다. 초기에는 이렇게 조건과 행동을 찾아내고 코딩으로 구현하는 것이 매우 순탄했다.

하지만, 그것은 정말 처음에만 그랬다. S5.10과 같은 미니 게임은 연역적인 방법으로 어느 정도의 최적화된 규칙들을 찾아낼 수 있었다. 그러나 조금만 문제가 커져도 직관적으로 찾아낸 규칙은 그다지 섬세하지 못하다는 것을 알게 되었다. 머지않아 예외 케이스를 발견하게 되고, 이에 대한 새로운 규칙의 추가가 계속 필요해졌다. 예외는 정말 끝도 없이 발생했다. 때로는 근본적인 새 아이디어가 떠올라서 규칙으로 구현해봤지만 결국 효과 면에서는 좋지 않은 경우도 많았다. “직관은 유쾌하지만 항상 옳은 것은 아니다.” 필자가 스스로 만들어 자주 읊는 경구인데, 딱 여기에 해당한다. 결국 나의 직관을 믿으며 수많은 규칙을 추가하고 수정을 거듭하는, 매우 성실한 코딩 과정을 통해 꽤 높은 성능의 에이전트를 만들 수 있었다. 하지만 수작업 코딩의 한계도 절감하게 되었다. 오히려 이는 지나치게 성실한 코딩이었고 이러한 코딩 자체를 차라리 컴퓨터에 맡기는 게 좋겠다는, 기계학습에 대한 수요를 몸소 체험할 수 있었다.

스트림스 게임을 하다 보면 나오지 않았으면 하는 숫자가 나오는 경우가 있다. 예를 들어, 말판에서 6과 8이 나란히 붙어 있는 상황에서 7을 배치해야 하는 경우다. 6, 7, 8을 연속적으로 넣어야 하지만, 이미 6과 8 사이에는 자리가 없으니 7을 다른 적당한 곳에 배치해야 한다. (나는 이 골치 아픈 문제를 해결하는 함수를 FindDump[]라고 이름 지었다.) 자, 어디에 배치하는 게 좋을까? 이런 골치 아픈 숫자들이 계속 나올 텐데 그때마다 어떤 전략을 써야 할까? 여러 가지 아이디어들을 규칙으로 추가하면서 코드는 계속 수정되어갔다. [그림6]은 규칙기반 방법에서 성실하게 코드를 수정해 가던 예들을 보여 준다.

수많은 규칙을 추가하고 수정하는 지루한 과정이었지만, 이를 통해 기저^baseline 방법을 확보할 수 있었다. 즉, 앞으로 다른 방법들이 만들어지면 비교실험이 가능해진 것이다.

규칙기반 방법은 인간이 어떤 게임을 정복하는 일반적인 방법이 아닐까 하는 생각이 든다. 판세의 다양한 패턴들을 범주화해서 이를 아우르는 일반적인 규칙을 만들게 되고, 이를 ‘정석’이란 이름을 붙이며 기억하게 된다. 때로는 이유를 묻지도 않고 정석은 어기면 안 되는 규칙이 되고, 이를 지식으로 전수해 나아간다. 그러면서 정석들은 점점 더 정교해진다. 즉, 규칙 기반 방법은 인간 사고과정과도 유사해서 코딩이 비교적 쉽다. 하지만 결국 처음에만 쉬울 뿐이고, 수많은 섬세한 규칙을 발견하고 검증해서 이를 추가해 나가는 과정은 매우 험난하다.

탐색기반 방법

규칙기반 방법과 달리 탐색기반 방법은 좀 더 컴퓨터에 의존적이라고 볼 수 있다. 물론 규칙기반 방법에서도 복잡한 조건 판단을 반복적으로 수행하기 위해서는 컴퓨터의 계산이 중요하지만, 이는 현재의 상황만을 중심으로 판단하는 것이고, 앞으로의 상황 예측에는 계산 자원을 거의 소비하지 않는다.

반면 탐색기반 방법에는 ‘몇 수 앞을 내다본다’는 관점이 개입되어 있다. 그리고 내다본 수에 기반하여 가장 유망한 곳에 말을 두게 된다. 기존의 복잡한 규칙들이 ‘가장 유망하다’라는 일반적인 규칙 하나로 대체된다. 그러다 보니 섬세한 규칙을 일일이 인간이 찾아내어 구현할 필요가 없어진다. 아래 [그림7]처럼 코드는 매우 간단해진다. 가장 유망하다는 판단의 근거가 되는 자료를 수집하는 데만 계산자원을 할당하면 된다. 이 판단을 위한 수읽기는 깊고 넓게 할수록 유리하지만, 계산 시간은 그만큼 많이 걸린다.

예를 들어, S5.10 미니 스트림스 게임에서 말판에 현재 비어있는 칸이 두 개가 있다고 하자. 이를 각각 s₁과 s₂라고 하자. 말판에 숫자 세 개가 있고 현재 넣어야 할 숫자 한 개 p가 알려져 있다면, 주머니에는 여섯 개의 숫자가 남아 있게 된다. 주어진 숫자 p를 넣을 위치 s_i를 결정하면(이 경우에는 s₁과 s₂중의 하나), 앞으로 만들어질 수 있는 말판의 경우의 수는 남아있는 숫자와 같아서 여섯 가지가 된다. 만약 높은 평균 점수를 추구하는 전략을 취한다면, 여섯 가지 경우 점수의 평균을 s_i를 선택한 기대값으로 볼 수 있다.

정말 간단하면서도 그럴듯한 방법이지 않은가? 하지만 문제는 ‘유망함’을 판단하기 위한 계산량에 있다. S5.10에서 비어 있는 칸이 두 개 대신, 세 개 있는 경우를 살펴보자. 이제 새롭게 주어진 수 p를 넣을 말판의 위치 s_i를 결정하고 나면, 비어있는 두 개의 칸에 남아 있는 일곱 개의 숫자를 순서 있게 배열할 수 있는 경우의 수는 42개이다. 이 42가지 경우 각각에 대해 평균을 계산하면 p를 어느 특정한 s_i에 배치하는 것에 대한 가치를 알게 된다. 빈칸이 세 칸이었으므로 n₃= 3*42 = 126가지 경우에 대한 계산을 해야 한다.

주머니에 m개의 숫자가 있고, 말판의 길이가 l인 일반적인 스트림스 게임 Sl.m에 대해서 생각해 보자. 말판에 빈칸이 q개 있을 때 어떤 빈칸에 숫자를 넣는 상황에 대한 기대값을 계산하기 위해서는, _(m–l+q-1)P_(q-1) 개의 서로 다른 경우를 고려해야 한다. 위에서 l = 5, m = 10, q = 3 이므로 ₇P₂= 7×6 = 42이고, 빈칸이 세 개 있으므로  3× ₇P₂= 126의 경우를 고려해야 다음 숫자를 넣을 최적의 위치를 알 수 있다 .

S5.10 에 대해서 요구되는 계산량을 따져 보자. 빈칸이 q개 있는 각 경우 별로 고려할 경우의 수는 다음과 같다.

따라서 한 번의 S5.10 게임을 완료하기 위해서는 위의 숫자를 모두 합한 16,603번의 경우에 대한 기대값 계산을 해야 한다. (물론 중복된 계산이 있지만, 이를 고려하지는 않았다.) 각 경우에 따라 말판에 숫자를 채우고, 그에 따른 예상 점수를 계산하는 일은 그리 비싼 계산이 아니므로, 매번 플레이마다 이를 반복하는 것은 (비록 비효율적이기는 하지만) 시간상으로는 충분히 가능하다. 실제로 S5.10을 탐색기반으로 한 번 플레이하는 데는 0.12초가 걸린다. (3.1 GHz i7, Mathematica 12 기준.) 반면 앞서 말한 규칙기반 방법으로 S5.10을 플레이하는 데는 0.0015초가 걸린다. 탐색기반 방법은 이보다 100배 정도 느린 셈이다. 탐색기반 방법의 이러한 문제는 본격적인 스트림스 게임인 S10.20이나 S20.30을 풀게 될 때 심각하게 드러난다. 먼저 S10.20의 경우 빈칸이 q개 있을 때 고려해야 할 경우의 수 n_q 다음과 같다.

그 크기가 S5.10에 비해 훨씬 큰 것을 알 수 있다. 한 번의 S10.20을 탐색방식으로 플레이하기 위해서는 무려 3.51927×10¹¹번의 경우를 고려해야 한다. 같은 계산환경을 가정하면 S5.10에 비해 2천만 배 이상(=2.11966×10⁷)의 시간이 걸린다. 약 28일에 해당한다. 본격적인 S20.30의 경우는 상황이 더 심각하다. 한 번의 S20.30을 탐색방식으로 플레이하기 위해서는 무려 5.03834×10²⁵번의 경우를 고려해야 한다. 계산시간은 9.62264×10¹³년이다. 우주의 나이(약 9.62264×10¹³년)보다도 긴 시간이 필요하다! (양자 컴퓨터는 이를 단축시켜 줄 수 있을까?)

즉, 탐색기반 방법을 통해 스트림스 게임의 복잡도를 수학적으로 가늠할 수 있었지만, 이 방법을 그대로 수행하는 것은 불가능하다는 것을 알 수 있다. (물론 탐색기반 방법을 근사하거나 가속하는 현대적인 기법들이 있지만, 여전히 한계는 있다.) 규칙기반 방법의 복잡한 코딩을 피하려고 상대적으로 구현이 간단한 탐색기반 방법을 살펴보았는데, 근사적 방법이나 계산 자원의 파격적인 할당 등의 적당한 보완책 없이는 그 실행이 터무니없이 비현실적이라는 것을 알게 되었다. 자, 그러니 이제 강화학습 방법을 시도해 볼 적당한 시점이 되었다.

1편은 여기서 마치고 이어지는 2편에서 심층강화학습을 소개하고 이를 스트림스 게임의 에이전트 제작에 사용한 예를 살펴보자.