스트림스 게임으로 시작하는 강화학습 [2]

강화학습 이해하기

복습합시다! 규칙 및 탐색기반 방법

이전 글 “스트림스 게임으로 시작하는 강화학습 [1]”에서 ‘오름차순 빙고’ 게임인 스트림스 게임의 규칙과 특징을 소개하였다.[1,2] 스트림스 게임을 스스로 플레이하는 에이전트를 만드는 방법으로 규칙기반 방법과 탐색기반 방법을 소개하였다. 각 방법은 명확한 장단점을 갖고 있는데, 특징을 요약하면 다음과 같다. 

규칙기반 방법: 섬세한 규칙을 일일이 입력하는 수작업 코딩의 ‘손맛’을 느끼기에는 적합하지만, 어느 정도 능선을 넘고 나면 매우 노동집약적인 방법이라는 것을 깨닫게 된다. 처음에는 ‘직관’에 의존하여 새로운 규칙을 찾아가는 것이 즐겁기도 하지만, 시행착오에 의존하는 경향이 강하고 체계적이지 않아서 어느 수준에 이르게 되면 더 이상 성능을 향상시키기 어렵다. 규칙들 간의 의존도가 강해서 작은 규칙의 변화에도 연결된 많은 부분의 코드를 함께 수정해야 하는 경우가 있다. 정성스러운 코딩을 통해 이런 어려움을 극복한다면 문제의 크기에 의존적이지 않고 안정적인 성능을 낼 수 있는 기저^baseline 코드를 확보할 수 있다. (버트런드 러셀의 ‘게으름에 대한 찬양’ 관점에서 보면 인간에게 지나친 성실함이 요구된다고 볼 수 있다.[3])

탐색기반 방법: 구현의 난이도 기준으로 보면 규칙기반 방법과 비교할 수 없을 만큼 간단하다. 탐색기반 방법은 수많은 규칙을 사람이 일일이 입력하는 대신, 컴퓨터를 이용해 가능한 모든 수(또는 많은 수)를 탐색하고 평가해서 가장 유망한 수를 결정한다는 전략이다. 즉, 세세하고 다양한 규칙들을 찾는 대신 ‘일반적인 탐색 전략’ 하나를 모든 경우에 적용하는 것이다. 확실히 코딩이 단순하지만, 실행 속도는 문제의 크기에 심각하게 영향을 받는다. 스트림스 게임을 예로 들면, S5.10과 같은 미니 게임에서는 탐색기반 방법이 전혀 문제가 없다. 하지만 S10.20이나 S20.30의 본격적인 스트림스 게임에는 도저히 적용할 수가 없는데, 이는 거대한 탐색 공간을 다루기에는 계산 자원에 현실적 한계가 있기 때문이다. (‘일반적인 탐색 전략’이라는 아이디어는 인간의 코딩 노동과 실수를 줄여 준다는 점에서 참 매력적이지만, 컴퓨터 한 대의 성실함만으로는 감당할 수 없는 문제들이 많다. 이 시대의 컴퓨터들에게는 성실함을 넘어 탁월한 지능이 요구되고 있다.)

그렇다면 강화학습 방법은 규칙 및 탐색기반 방법의 이런 단점을 극복하고, 구현과 탐색의 효율 모두를 만족시켜 줄 수 있을까? 아래에서 그 답을 찾아보자.

강화학습의 기본개념

이전 글 “스트림스 게임으로 시작하는 강화학습 [1]”에서 스트림스 게임의 성패는 매 순간 선택의 결과가 모두 모여 결정된다고 이야기했다. (물론 운도 크게 작용한다.) 지금까지 좋은 선택을 해왔다고 해도, 결정적인 순간에 한 번의 실수를 하게 되면 고득점을 얻는 데 치명적이다. 마지막까지 좋은 선택을 계속해야 최종적으로 고득점을 얻을 수 있다. 이러한 순차적 선택의 문제^{sequential decision problem}는 우리 주변에서 쉽게 찾아볼 수 있다. 대부분의 컴퓨터 게임이 그러하고, 로봇 제어의 문제도 관련이 있다.

이러한 순차적 선택의 문제를 선택과 보상의 개념을 도입하여 해결하겠다는 것이 강화학습의 기본 아이디어다. “어떻게 하면 매순간마다 좋은 선택을 하여 높은 보상을 받을 수 있을까? 어떻게 하면 보상들의 합을 최대로 만들 수 있을까?” 이러한 문제 해결에 적합한 기계학습 방법이 강화학습이다. [그림1]처럼 강화학습은 다른 기계학습과 다른 독특한 구성을 갖고 있다. 우선 이를 살펴보자.

강화학습에서 에이전트^agent는 문제를 해결하는 대행자이다. 환경^environment에서 얻은 경험과 보상^reward에 기반하여 현재 상태^state에서 취할 수 있는 최선의 행동^action을 배워나간다. ([그림1]) 이 점에서 정답 데이터가 미리 주어지고 이를 배우는 (또는 외우는) 지도학습^{supervised learning}과는 크게 다르다. 강화학습에서는 미리 만들어진 교과서나 참고서가 없다. 아무런 사전지식 없이 미지의 환경에서 맨몸으로 부딪히며 배우는 수밖에 없다. 시행착오^{trial-and-error}방식이기 때문에, 일단 환경에 행동을 가하고 그에 따른 보상 또는 벌칙을 받으며 그 상황에서의 선택에 대한 가치를 배워 나간다. (아이가 걸음마를 배우는 것과 같다. 잘하면 엄마가 박수를 쳐주고 웃어 주지만, 실패하면 엉덩이가 매우 아프다.)

처음에는 아무런 사전 지식도 없고 전략도 없기 때문에 에이전트 스스로 일련의 경험 데이터를 수집하고, 이로부터 나름의 선택 기준을 세워나가야 한다. 이렇게 충분히 시간이 흐르다 보면 세상을 보는 안목과 상황에 대처하는 판단력이 키워진다. 하지만 모든 것이 에이전트의 역할은 아니다. 보상을 정의하는 ‘개발자’의 역할도 중요하다. (보상을 어떻게 설정하는지는 강화학습의 중요한 연구분야이기도 하다.) 만약 보상을 주는 기준이 적절하지 않다면 아무리 시간이 흘러도 에이전트의 판단력은 향상되지 않을 수 있다. 오히려 ‘나쁜 버릇’이 생겨서 이를 고치지 못하게 되기도 한다.

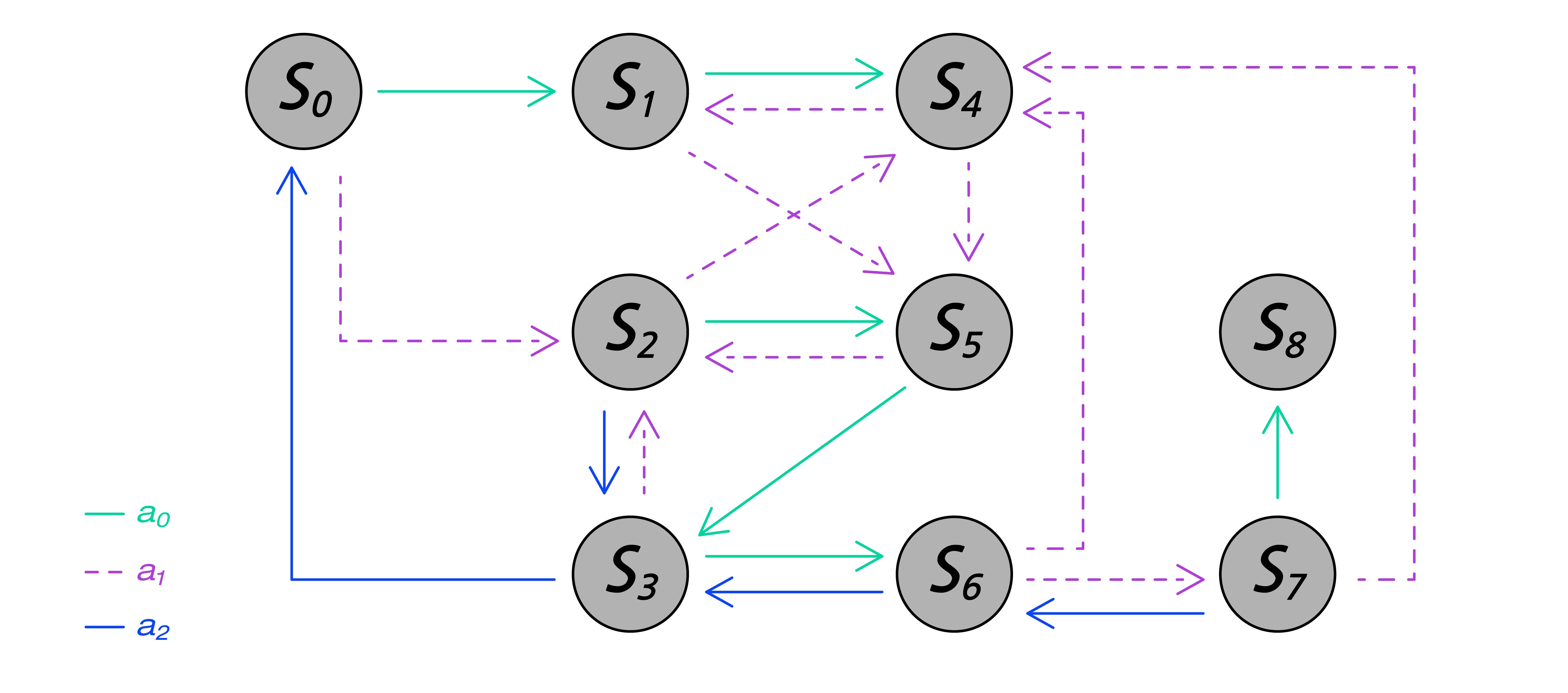
어떻게 보면 당연하지만 아직은 모호한 이 아이디어를 어떻게 컴퓨터에서 구현해야 할까? 이를 위해 우리는 문제를 좀 더 형식에 맞춰 정리해 볼 필요가 있다. 특히, 상태^state와 전이^transition의 개념이 필요하다. ([그림2])

시간에 따른 상황의 변화가 있을 때 이를 상태^state와 전이^transition로 표현할 수 있으면 편리하다. 하나의 상태는 관찰 가능한 여러 가지 값들로 표현된다. 상태 전이는 하나의 상태에서 다른 상태로 변경되었다는 의미인데, 주로 현재 상태에서 어떤 행동을 취했을 때 다음 상태로의 전이가 발생한다. 따라서 시작 상태에서 일련의 행동을 취하게 되면 상태 전이가 계속된다. [그림2]에서 \(s_i\)는 상태이고, \(a_i\)는 행동이다. (슈퍼마리오 게임이라면, 방향키를 누르는 것이 행동을 취하는 것이고, 그에 따라 마리오가 어떤 방향으로 달리거나 점프를 하는 것이 상태의 변화에 해당한다.)

만약 새로운 상태에 도달할 때마다 보상(또는 점수)이 발생한다면, 이 보상들의 합을 최대로 만드는 것이 우리의 목표이다. 중간 상태에서는 보상이 발생하지 않고 최종 상태에서만 발생하는 경우도 있는데, 이때는 최종 점수만 고려하면 된다. (슈퍼마리오 게임에서는 적을 없애거나 코인을 얻을 때마다 점수가 누적되지만, 바둑에서는 매번 두는 수마다 보상이 발생하지 않는다. 바둑은 마지막에 승패로 보상이 주어진다.)

그렇다면 미래를 모르는 상황에서, 각 상태에서 어떤 선택을 하는 것이 최선일까? 선택의 가치를 판단하는 기준이 있을까? 강화학습은 미지의 환경에서 경험 축적을 통해 선택의 기준을 학습한다. 반복적인 학습을 통해 선택의 기준을 개선해가는 과정이 강화학습의 핵심이다. 어쩌면 오랜 경험을 통해 각 상태에서 받을 미래 보상을 모두 기억해 나가는 것으로도 볼 수 있다. 각 상태에서 구체적인 최선의 행동을 선택하는 것을 ‘정책^policy’을 따른다고 한다. 보통 정책을 \(π\)로 표현한다. 강화학습의 최종 목표는 우수한 정책을 학습하는 것이다.

여기까지는 강화학습의 가장 기본적인 개념들이었다. 아래에서는 강화학습 적용을 위해 이 개념들을 좀 더 구체화해 보자.

강화학습의 적용

어떤 문제에 강화학습 기법을 적용하기에 앞서, 그 문제가 특정 조건을 만족시키는지 우선 살펴봐야 한다. 이를 전문 용어로는 마코프 결정 과정^{MDP, Markov Decision Process}으로 모델링 가능한지 살펴본다고 한다. 복잡한 용어 같지만 개념은 간단하다. 먼저 현재 상태에서 다음 상태로의 상태 전이는 오로지 현재 상태에만 영향을 받고, 이전의 어떠한 상태에도 전혀 영향을 받지 않아야 한다. 이를 마코프^Markov 성질이라고 한다. 내일의 날씨를 오늘의 날씨로는 예측할 수 없다는 점에서, 날씨 변화는 마코프 성질을 따르지 않는다. 반면에 대부분의 보드게임들은 다음 상태로의 진행이 현재 상태와 던져진 주사위로 결정되기 때문에 마코프 성질을 따른다.

어떤 문제가 마코프 성질을 갖고 있다면, 그 문제를 아래와 같은 MDP 형식^formalism으로 기술할 수 있다. (그림 참조)

1. 상태^state \(S\) : 에이전트가 관찰할 수 있는 환경의 상태 \(s_i\)들의 집합 
2. 행동^action \(A\): 에이전트가 환경에 취할 수 있는 모든 행동 \(a_i\)들의 집합 
3. 전이 확률^{transition probability} \(P\) : 상태 \(s\)에서 행동 \(a\)를 수행했을 때 상태 \(s’\)로 옮겨 갈 확률
4. 보상^reward \(R\) : 상태 \(s\)에서 행동 \(a\)를 수행하고 상태 \(s’\)로 옮겨가며 환경에서 받는 보상
5. 감가율^{discount rate} \(γ\): 미래에 받을 보상에 대한 신뢰도. \(0\)에서 \(1\) 사이의 수

MDP의 위 구성요소들 중에서 ‘감가율’은 조금 어렵게 느껴질 수 있다. 이는 보상의 미래 가치와 관련이 있는데, 뒤에서 설명과 예를 통해 다시 살펴볼 예정이다.

이제 위에서 설명한 MDP 형식으로 스트림스 게임을 기술해 보자. (여기서부터는 이전 글 “스트림스 게임으로 시작하는 강화학습 [1]”에서 설명한 스트림스 게임의 규칙에 대한 이해가 필요하다!)

1. 상태 \(S\) : 스트림스 게임의 상태는 현재의 말판^slot \(s\)와 새롭게 배치해야 할 말^number \(n\)으로 이루어진다: \([s|n]\). 예를 들어, 스트림스 미니 게임 S5.10의 상태는 말판 \(s\)의 크기 5와 새롭게 넣을 수 1개를 포함하여 6개의 숫자로 구성된다. 예를 들어, 현재 말판이 \([0, 3, 0, 8, 0]\)이고 새롭게 넣을 수가 5라고 한다면, 상태를 \([0, 3, 0, 8, 0 | 5]\)와 같이 표시한다. (0은 숫자가 차지 않은 빈칸을 의미한다.)
2. 행동 \(A\) : 입력할 말을 배치할 수 있는 빈칸의 위치가 액션에 해당한다. 즉, 특정 액션은 슬롯의 특정 위치를 의미한다. 현재 말판이 \([0, 3, 0, 8, 0]\)이라면 첫 번째, 세 번째, 다섯 번째 칸이 비어 있으므로, 취할 수 있는 액션 집합은 \(A = {1, 3, 5}\)이다.
3. 전이 확률 \(P\) : 새로운 상태 \(s’\)는 이전 말판에 숫자를 입력하고 새롭게 입력할 숫자로 구성된다. 새롭게 입력할 숫자는 현재 주머니에서 남아 있는 숫자들 중에서 임의로 선택된다. 현재 상태 \(s=[0, 3, 0, 8, 0 |5]\)에서 액션을 \(a=3\)으로 취하고, 새로운 입력 숫자 10을 받는다면 새로운 상태는 다음과 같다: \(s’ = [0, 3, 5, 8, 0 |10]\). 이때 \(s\)에서 \(s’\)로의 전이 확률은 \({3, 5, 8}\)을 제외하고 남은 숫자 7개 중에서 하나를 선택한 것이므로, \(P(s, s’)\)는 \(\frac { 1 }{ 7 }\)이 된다.
4. 보상 \(R\) : 스트림스 게임에서 보상은 마지막에만 주어진다. 즉, 말판이 모두 채워져 점수를 계산할 수 있을 때 보상이 주어진다. 중간 단계에는 보상이 주어지지 않으므로 중간 단계의 보상은 0이다. (보상을 정의하는 정해진 규칙은 없으며, 보상을 어떻게 설정하느냐는 학습에 큰 영향을 줄 수 있다. 문제에 따라 보상 설정은 MDP의 가장 어려운 과정이 될 수 있다.)
5. 감가율 \(γ\): 강화학습에서는 현재의 보상뿐만 아니라 미래의 보상도 함께 고려한다. 감가율은 미래에 받게 될 보상에 대한 불확실성을 고려한 신뢰를 표현한다. 감가율은 \(0\)과 \(1\) 사이의 값을 사용한다. (스트림스 게임 실험에서는 \(γ = 0.99\)를 사용했다.) 만약 앞으로 세 수 후에 받게 될 보상이 \(r_3\)이라고 할 때, 미래를 전적으로 신뢰하면 \(γ = 1\)로 설정하여 감가되지 않은 보상을 받을 것으로 예측하면 된다: \(γ^3r_3 = r_3.\) 하지만 불확실성 등의 이유로 \(γ = 0.7\)의 감가율을 설정하면 미래의 보상의 가치를 낮춰서 예상하게 된다: \(γ^3r_3 = 0.343 r_3\).

위의 MDP 모델을 바탕으로 아래에서는 강화학습의 기본적인 방법인 큐러닝^Q-Learning을 설명하고, 큐러닝에 심층신경망^{DNN, Deep Neural Net}을 결합한 심층큐러닝^{DQN, Deep Q-Learning} 방법을 설명하고자 한다.

강화학습 방법 1. 큐러닝^Q-Learning

위에서는 스트림스 게임을 MDP로 모델링해 보았다. 이를 바탕으로 강화학습의 가장 기본 방법인 큐러닝^Q-learning을 스트림스 게임에 적용해 보자. 큐러닝에서 큐^Q는 어떤 상태 \(s\)에서 취한 행동 \(a\)의 가치^quality를 의미한다: \(Q(s,a) = q\). 이 큐값^Q-value들을 테이블에 저장하기 때문에 큐테이블^Q-table 방법이라고도 한다. 큐러닝 의 의미를 조금 자세히 설명하기 위해 몇 가지 수식을 소개할 예정이다.

수식들은 생각보다 복잡하지 않아서 천천히 읽어 보면 누구나 대강의 맥락은 이해할 것이다. 하지만 강화학습 이론의 중요한 기본이므로 본격적인 강화학습 공부와 에이전트를 직접 구현해 보고 싶은 분들은 정확한 이해를 권한다. (강화학습 관련 전문서적으로는 서튼^Sutton과 바트로^Barto의 『강화학습 소개 ^{Reinforcement Learning: An Introduction}』가 가장 유명하다.[4] 필자가 번역에 참여한 입문자용 서적도 있다.[5]) 강화학습의 최종목표를 좀 더 상세히 기술해 본다면, 특정 상태 \(s\)에서 최선의 행동 \(a\)를 선택하게 해주는 정책 함수 \(π\)를 만드는 것이다: \(π(s) = a\). 그렇다면 ‘최선’이란 정확히 어떤 의미일까? 이를 위해 상태의 가치와 행동의 가치를 정의해 보자.

현재 상태 \(s_t\)에서 선택한 행동 \(a_t\)의 가치는 다음 상태 \(s_{t+1}\)로 전이해서 받게 되는 보상 \(r_{t+1}\)과 그 이후에 받는 모든 보상들의 총합으로 평가할 수 있다. 이러한 미래 보상들의 합^{total future reward}을 총 누적보상^return이라고 하며, 다음과 같이 표현한다:

\begin{equation}
R_t = r_{t+1} + r_{t+2} + \cdots + r_{T}
\quad \cdots \quad (1)
\end{equation}

위 식에서 각 보상 \(r_{t+1}\)은 상태 \(s_t\)에서 취한 액션 \(a_t\)로 인해 상태 \(S_{t+1}\)에서 받은 보상이다. 따라서 총 누적보상 \(R_t\)은 상태 \(s_t\)에서 출발하여 마지막 상태 \(s_T\)까지 거치면서 받을 모든 보상의 합이다.

그런데 총 누적보상 개념에는 한가지 고려되지 않은 것이 있다. 바로 미래에 대한 불확실성이다. (예를 들어, 게임에서 등장하는 적이 어떻게 늘 같은 위치에만 있겠는가?) 이러한 불확실성을 고려한다면, 현재 계산한 미래 보상을 액면 그대로 받아들이기 어렵다. 아마도 다소 낮추어 보수적으로 계산하는 것이 안전할 수 있다. 이러한 조정의 역할을 하는 것이 MDP의 감가율 \(γ\)이다. (이론적으로는 반복적인 학습 후에 보상값의 수렴을 보장하는 중요한 역할을 하기도 한다.[6]) 감가율을 0으로 두면 미래의 보상을 전혀 고려하지 않는 것이고, 감가율을 1로 두면 미래의 보상을 무조건 신뢰하는 것이다. 감가율을 고려한 감가된 미래 보상^{discounted future reward}으로 총 누적보상을 다음과 같이 표현할 수 있다:

\begin{equation}
R_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots + \gamma^{T-t-1} r_{T} = r_{t+1} + \gamma R_{t+1}
\quad \cdots \quad (2)
\end{equation}

따라서 어떤 상태 \(s_t\)에서 선택한 특정 액션의 가치는 감가된 미래 보상 \(R_{ t }=r_{ t+1 }+\gamma R_{t+1}\)으로 가늠할 수 있다. 이를 더 정확히 계산하기 위한 개념이 상태가치함수^{state-action value function}이다.

특정 정책 \(π\)을 행동 선택한다고 할 때, 상태가치함수 \(Vπ(s)\)는 어떤 상태 \(s\)에서 기대할 수 있는 총 누적보상 \(R_t\)의 기대치이다. 특정 액션을 고려하지 않고 상태에만 관련된 값이며, 총 누적보상의 예상 평균값이라고 볼 수 있다.

\begin{equation}
V^\pi(s) = \mathbb{E}_\pi\left[ R_t | s_t = s\right] =
\mathbb{E}_\pi \left[ \sum_{k=0}^{\infty} \gamma^k r_{t+k+1}| s_t = s \right]
\quad \cdots \quad (3)
\end{equation}

상태-행동 가치함수는 큐함수^Q-function라고도 하는데, 정책 \(π\)를 따라 특정 상태에서 특정 액션을 취할 때의 가치를 나타낸다. 상태-행동 가치함수는 상태가치함수와 유사하게 총 누적보상의 기대치인데, 특정 액션 \(a\)에 대한 경우로 한정한다.

\begin{equation}
Q^\pi(s,a) = \mathbb{E}_\pi\left[ R_t | s_t = s, a_t = a \right] =
\mathbb{E}_\pi \left[ \sum_{k=0}^{\infty} \gamma^k r_{t+k+1}| s_t = s, a_t = a \right]
\quad \cdots \quad (4)
\end{equation}

큐함수를 이용하여 정책 함수를 정의하면 다음과 같다. 즉, 어떤 상태에서 최고의 상태-행동 가치를 주는 액션 \(a\)를 선택하는 것이다.

\begin{equation}
\pi(s) = \mathrm{argmax}_{a’}Q(s,a’) =a
\quad \cdots \quad (5)
\end{equation}

즉 큐함수는 어떤 정책 \(π\)이 행동을 선택하는 기준이다. 큐러닝은 바로 이 큐함수를 찾는 강화학습 방법의 하나이다. 큐함수를 찾는 가장 기본적인 방법은 벨만 방정식^{Bellman equation}을 이용해서 재귀적으로 큐함수를 정의하고, 이를 순차적으로 업데이트하는 방법이다.[4,5] 큐함수에 대한 벨만 방정식은 다음과 같이 표현할 수 있다.

\begin{equation}
Q^\pi(s,a) = \sum_{s’} P^{a}_{s s’} \left[ R^{a}_{s s’} + \gamma
\sum_{a’} Q^\pi(s’, a’)\right]
\quad \cdots \quad (6)
\end{equation}

위 식에서 \(P^{a}_{s s’}\)는 상태 \(s\)에서 액션 \(a\)를 취해서 \(s’\)로 상태가 전이할 확률이고, \(R^{a}_{s s’}\)는 이때 받는 보상이다. 이 식은 상태 \(s\)에서 액션 \(a\)를 취할 때 전이할 수 있는 상태가 다양한 경우를 가정하고 있다. 만약 전이 상태가 \(s’\)로 정해져 있다면 식은 더 간단하게 표현된다.

\begin{equation}
Q^\pi(s,a) = R^{a}_{s s’} + \gamma \sum_{a’} Q^\pi(s’, a’)
\quad \cdots \quad (7)
\end{equation}

큐러닝^Q-learning에서는 위의 재귀식을 더 간단히 표현한다. 즉, 상태 \(s\)에서 액션 \(a\)를 취하고 보상 \(R^{a}_{s s’}\)를 받고 \(s’\)상태로 전이했다고 할 때, 새로운 상태-행동 가치값 또는 큐값^Q-value을 다음과 같이 재귀적^recursive으로 업데이트한다.

\begin{equation}
Q^\pi(s,a) = R^{a}_{s s’} + \gamma \max_{a’} Q^\pi(s’, a’)
\quad \cdots \quad (8)
\end{equation}

여기서 새로운 개념이 또 등장하는데, 바로 학습률^{learning rate} \(α\)이다. 감가율이 미래에 대한 신뢰의 문제를 다루었다면, 학습률은 현재 경험에 대한 신뢰의 문제를 다룬다. 즉, 학습 초반에는 상태-행동-보상에 대한 경험이 부족하기 때문에 이에 근거해서 만든 큐함수와 정책을 그대로 믿기는 어렵다. 따라서 미숙한 정책을 그대로 따를 바에는 새로운 경험에서 얻은 가치를 함께 고려하는 것이 좋다. 하지만 충분한 경험을 쌓은 학습 후반부에는 전혀 새로운 경험을 만나게 될 가능성이 작고, 큐함수와 정책도 성숙한 편이라 그대로 신뢰하는 편이 좋다.

즉, 현재의 큐함수가 추정한 가치와 새로운 경험을 고려한 가치 사이의 비중을 학습률 \(α\)로 조정하게 된다. 수식으로 표현하자면, 현재의 큐함수 \(Q^\pi(s,a)\)가 제시한 가치와 새로운 경험을 고려한 재귀적 가치(수식 8)를 \(α\)값으로 선형 보강한 중간값으로 큐값을 업데이트하게 된다.

\begin{eqnarray}
Q^\pi(s,a) & \leftarrow& (1-\alpha) Q^\pi(s,a)
+ \alpha(R^{a}_{s s’} + \gamma \max_{a’} Q^\pi(s’, a’)) \nonumber \\
&=& Q^\pi(s,a) + \alpha\left( R^{a}_{s s’} + \gamma \max_{a’} Q^\pi(s’, a’) – Q^\pi(s,a)
\right)
\quad \cdots \quad (9)
\end{eqnarray}

만약 상태전이가 확률분포 \( P^{a}_{s s’}\)를 따른다면 다음과 같이 표현 가능하다.

\begin{equation}
Q^\pi(s,a) \leftarrow (1-\alpha) Q^\pi(s,a)
+ \alpha \sum_{s’} P^{a}_{s s’} \left[ R^{a}_{s s’} + \gamma
\sum_{a’} Q^\pi(s’, a’)\right]
\quad \cdots \quad (10)
\end{equation}

이러한 큐함수는 충분한 반복 업데이트를 통해 최적값으로 수렴하는 것으로 알려져 있다.[6] 학습률은 0과 1사이의 값에서 선택하게 된다. 보통 학습의 초반에는 큰 값을 넣어서 새로운 경험에 대한 가중치를 더 주고, 학습이 진행될수록 작은 값을 사용해서 현재의 정책을 신뢰하도록 한다.

강화학습에서 경험 수집의 중요성은 앞에서 강조한 바 있다. 이와 관련해서 경험 수집 방식을 제어하는 탐험률^{exploration rate}의 개념이 필요하다. (참고: 앞에서 설명한 학습률 \(α\)는 경험이 모두 수집된 후에 큐함수를 업데이트할 때 사용하는 값이다.) 만약 현재 학습한 정책을 100% 신뢰하고 경험을 수집하면 새로운 경험, 또는 지금까지보다 더 높은 보상을 주는 경험을 만날 확률이 높지 않다. 가끔은 기존 정책을 과감히 탈피하여 미지의 경험에 대한 탐험을 통해서 전혀 새로운 수준의 보상을 추구하기도 해야 한다. 강화학습에서 현재의 정책을 그대로 따르는 것을 수확^exploitation라 하고, 현재의 정책을 무시하고 새로운 가능성을 추구하는 것을 탐험^exploration이라고 한다. 이러한 수확-탐험^{exploitation-exploration}의 조화는 강화학습에서 중요한 시스템 변수인데, 이러한 수확과 탐험의 비율을 탐험률 \(ϵ\)라고 한다.

큐러닝을 구현하는 간단한 방법은 큐함수를 \(<s, a, Q>\)의 테이블로 표현하고, 이를 반복적으로 업데이트하는 것이다. 이 테이블을 큐테이블^Q-table이라고 한다.

단순한 문제라면 큐테이블로 큐함수를 표현하는 데 별 문제가 없다. 하지만 문제의 크기가 조금만 커져도 큐테이블의 크기는 폭증하는 것이 보통이다. 이 경우 테이블 검색, 개별 항목의 업데이트와 기타 관리에 많은 계산 자원이 필요하다. 예를 들어, 스트림스 미니 게임 S5.10의 경우 가능한 상태-행동 쌍 \(<s , a>\)의 개수는 63,590개이다. 하지만, 본격적인 스트림스 게임인 S10.20는 상태-행동 쌍이 약 1.56*10¹²개에 이르고, S20.30의 경우는 3.78*10²⁶개가 된다.

상태-행동 가치함수를 큐테이블로 표현하는 것이 현실적으로 불가능한 대규모 문제에서, 테이블 대신 심층신경망을 사용한 것이 심층큐러닝^{Deep Q-Network}의 탄생배경이다. 아래에서는 심층큐러닝을 위해 큐러닝에서 수정된 부분을 중심으로 살펴보자.

강화학습 방법 2. 심층큐러닝^{Deep Q-Network, DQN}

ATARI 2600은 1980년대를 풍미한 고전 콘솔 게임기로, 팩맨^Pac-Man 등의 유명한 게임을 포함하고 있다. 2013년에 구글 딥마인드^{Google DeepMind}는 이 유명한 고전 게임들을 인간 수준으로 플레이하는 에이전트를 만든 연구를 소개했다. 이때 사용한 방법이 바로 심층큐러닝^{DQN, Deep Q-Learning} 방법이다.[7,8] 

심층큐러닝 방법은 앞에서 설명한 큐러닝과 딥러닝의 결합이다. 특히 큐값을 저장하는 테이블 대신에 심층 신경망으로 큐함수를 표현한다. 이를 큐신경망^Q-Net이라고 한다. 현재의 큐함수를 이용한 정책으로 새로운 경험을 수집하는 과정은 기존의 큐러닝과 완전히 동일하다. 하지만 이 경험들을 이용하여 큐함수를 업데이트하는 과정에서 차이가 있다.

심층큐러닝에서는 큐함수가 심층신경망으로 표현되어 있기 때문에, 값을 업데이트할 때는 딥러닝의 역전파^{back propagation}방법을 사용한다.[9] 이는 일반적인 지도학습 방법과 동일한데, 이때 학습할 데이터가 바로 기존의 큐테이블에 저장된 경험들이다. 즉, 상태-행동 쌍 \(<s, a>\)이 데이터가 되고 이때의 큐값 \(q\)값이 주석정보^annotation가 된다.

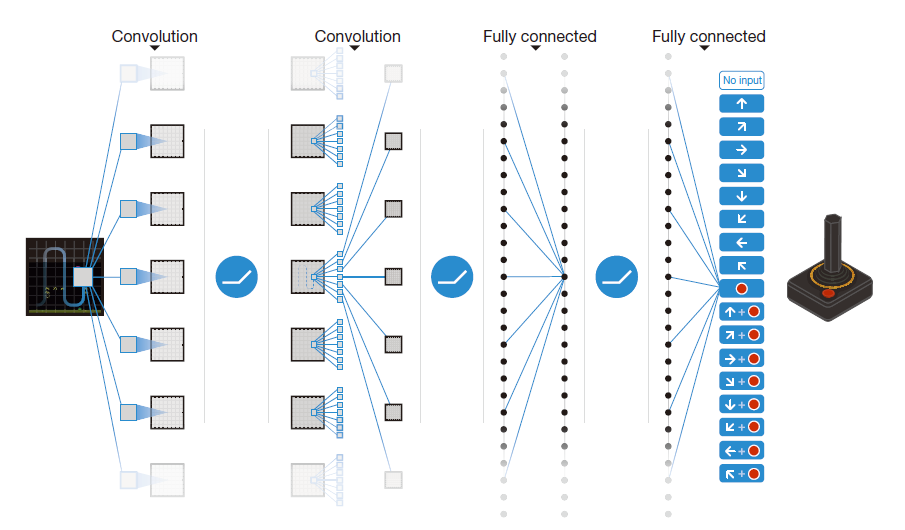
딥러닝과 심층신경망이 익숙하지 않은 독자들을 위해서 요약하자면 다음과 같다. 신경망은 데이터를 분류^classify하거나 값을 추정^regress하는데 사용하는 기계학습 방법이다. 주어진 이미지에 고양이가 있는지 아니면 강아지가 있는지를 알아내는 것은 분류의 기능이고, 며칠 동안 관찰한 온도를 기반으로 내일의 날씨를 예측하는 것은 추정의 기능이다. 위에서 설명한 큐신경망은 큐값을 추정하는 기능을 한다. 그런데 상태-행동 쌍의 개수가 대단히 많고, 그 경우도 매우 다양하게 되면 일반적인 신경망으로는 표현이 어렵다. 이때 신경망의 층을 더 높이 쌓아 올린 심층신경망을 사용하는 것이다. 그림은 아타리 게임을 해결한 DQN의 심층신경망 구조를 보여준다.

심층큐러닝 강화학습의 구현은 크게 두 부분으로 되어 있다. 첫 번째는 경험을 수집하는 부분이고 두 번째는 큐함수를 업데이트하는 부분이다. ([그림5] 참조) 경험을 수집하는 부분은 환경에서 상태를 읽어서 정책을 통해 큐함수를 업데이트하는 부분이다. 경험을 수집하는 부분은 환경에서 상태를 읽어서 정책을 통해 결정된 행동을 환경에 입력하여 새로운 상태와 보상을 받는 과정을 포함한다. (탐험률 \(ϵ\)에 따라 무작위 행동을 고르기도 한다.) 이때 수집된 경험값들을 메모리^{experience memory}에 저장하고 두 번째 단계에서 큐함수 심층신경망을 업데이트할 데이터로 사용한다. 경험 메모리에 저장되는 큐값은 학습률 \(α\)를 적용하여 기존의 큐함수에서 얻은 값과 벨만 방정식으로 만든 새로운 큐값을 혼합하여 업데이트한다.

강화학습에서 환경은 게임 엔진이나 로봇 시뮬레이터에 해당한다. 주로 복잡한 모델이 구현되어 있기 때문에 CPU에서 구동되는 것이 일반적이다. 환경에 입력할 행동을 선택할 때는 정책의 큐함수를 활용해야 한다. 이때 큐함수는 심층신경망으로 되어있기 때문에 GPU로 계산하게 된다. 이는 신경망에 대한 순전파^{forward propagation} 과정이므로 학습과정과는 다르다. 탐험률 \(ϵ\)는 경험을 수집하는 과정에서 사용된다. 난수 발생기를 통해 얻은 값이 미리 지정한 탐험률보다 크면 정책이 결정한 행동을 취하고, 그렇지 않으면 정책을 따르지 않고 무작위 행동을 선택한다.

수집된 경험 데이터로 큐함수 자체를 업데이트할 때는, 딥러닝 지도학습에서 역전파^{back propagation}로 신경망을 수정하는 것과 같다. 다만 일반적인 딥러닝 지도학습에서는 동일한 데이터를 반복적으로 학습하게 되지만, 심층강화학습에서는 새롭게 수집한 경험 데이터로 매번 다르게 학습을 하게 된다.

이상으로 심층큐러닝 방법을 간단히 소개하였다. 아래에서는 심층큐러닝 방법으로 스트림스 게임 에이전트를 만든 경험을 소개하고자 한다.

강화학습으로 스트림스 게임 에이전트 만들기

아래에서는 드디어 심층큐러닝^DQN 강화학습 기법을 스트림스 게임에 적용한 이야기를 다룬다. 특히 학습과정에서 발견한 흥미로운 관찰과 해결해야 할 문제들도 함께 소개하니, 스트림스 게임 에이전트의 성능 개선에 관심 있는 여러분들의 도전을 기대해 본다.

S5.10

심층큐러닝의 의미를 이해했고, 문제를 MDP로 모델링했다면(이전 글 “스트림스 게임으로 시작하는 강화학습 [1]” 참조), 이를 코드로 구현하는 것은 크게 어렵지 않다. 다만 학습에 필요한 각종 시스템 인수값들 (예를 들어, 학습률 \(α\), 감가율 \(γ\), 탐험율 \(ϵ\))을 설정하는 과정에서 시행착오를 반복하기 쉽다. 스트림스 미니게임 S5.10 를 위한 에이전트는 앞에 설명한 기본 시스템 인수 값으로도 괜찮은 성능을 학습할 수 있었다: 예, \(ϵ = 1.0\).

스트림스 S5.10 에 대해 규칙기반, 탐색기반 방법과 강화학습 방법으로 에이전트를 만들었을 때, 그 성능은 아래 표와 같이 비교할 수 있다. 큐러닝 방법이 규칙·탐색기반 방법에 비해 우수함을 알 수 있다.

[그림7]에서 상태 개수는 게임 에이전트가 상태 전이를 통해 방문한 모든 상태의 개수를 의미한다. (상태 전이를 그래프로 그리면 최초 상태 \([0,0,0,0,0|0]\)을 루트로 하는 트리 그래프를 그릴 수 있는데, 상태 개수가 많다는 것은 그래프의 노드가 많은 것과 같은 의미이다.) 흥미로운 것은, 규칙기반 방법이 탐색기반 방법에 비해 더 많은 상태를 방문하고도 더 낮은 점수를 얻었다는 것이다. 이는 규칙 기반 방법을 위해 수동으로 찾은 세부 규칙의 효율이 그다지 높지 않다는 것으로 해석할 수 있다.

큐러닝 방법의 상태의 개수는 더욱 흥미롭다. 규칙·탐색기반 방법에 비해서 방문한 상태가 압도적으로 많다. 이는 강화학습 과정에서 다양한 경험 축적을 통해 섬세한 내부 전이 규칙들을 찾아내었기 때문이다. 즉, 더 다양한 상태의 가치를 고려했다는 의미이기도 하다. 그리고 심층큐러닝 방법이 큐테이블 방법에 비해 더 적은 상태를 방문했는데, 이는 신경망을 이용한 큐함수 표현이 유효하며 또한 효율적이기 때문이라고 생각된다.

이렇게 미니 스트림스 게임 S5.10을 다양한 방법으로 풀어보고 성능을 비교해 심층강화학습의 의미와 구현 과정을 조금 더 이해할 수 있었다. 이제 준비운동을 마쳤다고 생각하고 드디어 본격적인 스트림스 게임 S10.20과 S20.30에 도전해보았다. S5.10경험을 살려 쉽게 우수한 성능의 에이전트의 얻을 줄 알았는데, 그 여정은 꽤나 험난했다.

S10.20

S5.10에 대한 강화학습 과정은 시행착오가 없이 한 번에 이루어졌다. 하지만 게임이 어려워질수록 학습과정은 쉽지 않다. 학습을 잘 하고 있는지를 살펴볼 기준이 필요하다. 따라서 S10.20 스트림스 게임을 다루기 전에, 에이전트의 성능을 평가할 가장 직관적인 지표로서, 첫수 전략^{first move}에 대해서 살펴보자.

스트림스 게임에서 첫수란 완전히 비어 있는 말판에 넣는 첫 번째 수를 의미한다. (오목이나 바둑에서 첫 번째 돌을 두는 것과 같다.) 이전 글 “스트림스 게임으로 시작하는 강화학습 [1]”에서 여러분들이 직접 스트림스 게임을 할 수 있는 방법을 소개했는데, 아마도 각자 첫수 전략을 세워야 했을 것이다. 첫수는 다른 수에 비해 비교적 단순한 판단만 하면 된다고 생각할 수 있다.

예를 들어, S5.10 같은 경우에 1이나 2가 나오면 맨 앞칸에, 9나 10이 나오면 맨 뒷 칸에 넣는 것이 일반적인 (그리고 나쁘지 않은) 첫수 전략이 될 수 있다. 이런 전략을 확장해서 각 숫자와 첫수의 위치를 그래프로 그려보면 대각선 모양을 예상할 수 있다. [그림9]는 첫수에 대한 큐값을 보여 주는데, 짙은 부분이 높은 값이다.

그런데 강화학습 에이전트는 수많은 경험에 기반해서 훨씬 섬세한 첫수 전략을 구사한다. 예를 들어, S5.10에서 큐러닝으로 학습한 에이전트는 2나 9를 첫수로 넣어야 할 때, 말판의 맨 뒷 칸 대신 끝에서 두 번째 칸에 배치한다. 이러한 현상은 S6.12에서도 발견된다. ([그림9])

이러한 관찰에 근거해서, S10.20의 에이전트를 강화학습으로 처음 만들었을 때에도 첫수 전략은 하나의 대각선을 이룰 것이라고 예상했다. 하지만 아래 [그림10]과 같이 두 개의 대각선이 발생해서 무척 놀랐다. (앞으로 이를 반푼이 현상이라고 부르자.) 그림에서는 붉은색이 높은 큐값이고 푸른색이 낮은 큐값이다.

분석해보니 이런 반푼이 현상은 탐험율 설정의 문제였다. 즉, S5.10에서처럼 탐험율을 100%로 설정하고(\(ϵ = 1.0\)) 학습을 했더니 기존 경험을 모두 무시하고 새로운 경험만 기억하려고 했던 것이다.

이 문제를 해결하기 위해 탐험율을 학습의 ‘경륜’에 맞춰 조정해주면 좋을 것 같았다. (이렇게 직관에 의존해서 값을 설정하는 것이 기존의 규칙기반 코딩의 수작업과 뭐가 다른가 하는 회의가 아직도 들지만…) 탐험율을 90%에서 시작해서 차츰 10%로 낮추어 주자 강한 단일 대각선이 형성되었다. 첫수가 만들어지는 과정은 다음 그림과 같다.

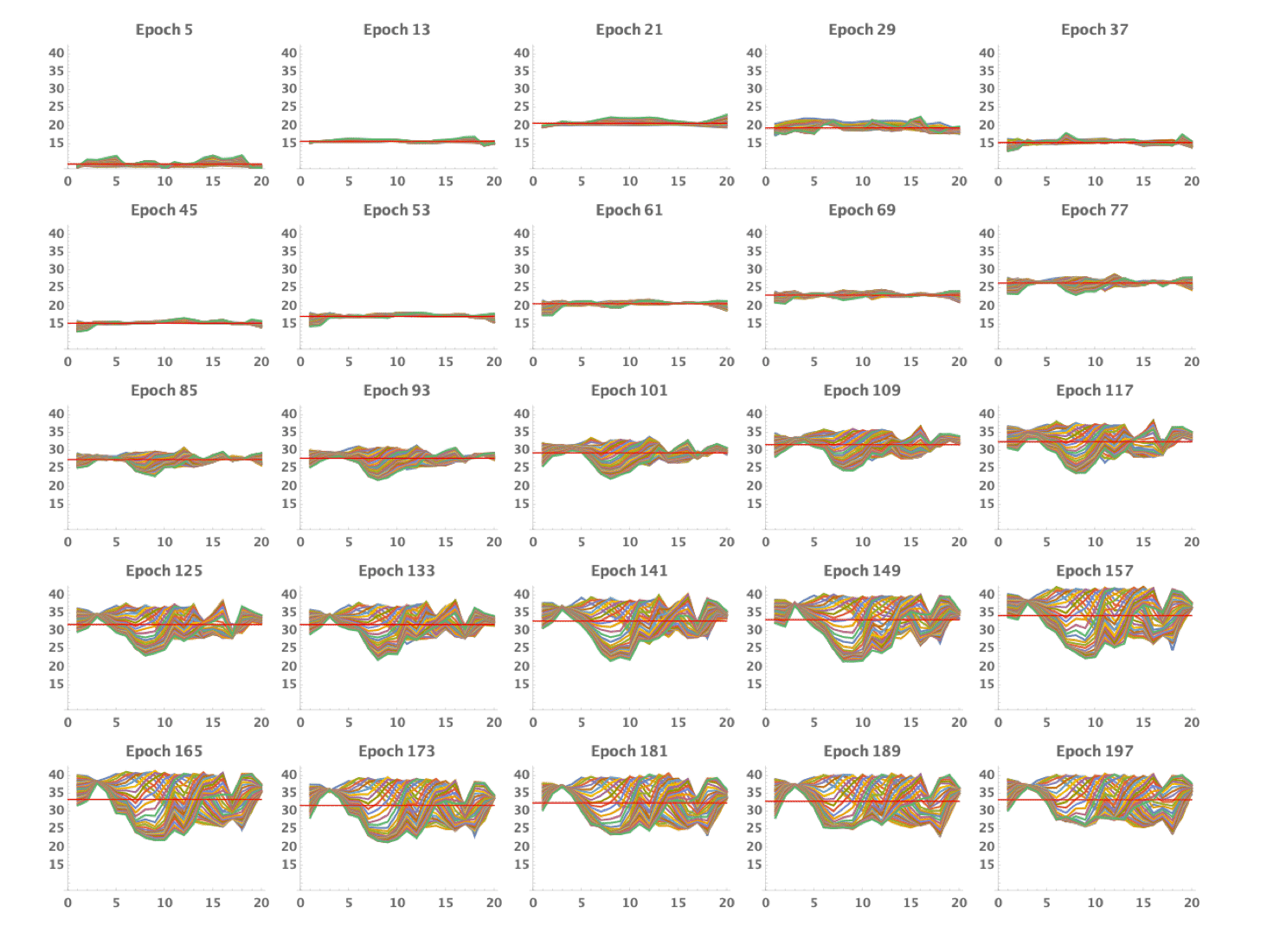
위 그림에서 시간이 갈수록 (또는 학습 epoch가 진행될수록) 첫수를 선택하는 패턴이 점점 뚜렷해짐을 알 수 있다. 패턴의 뚜렷함 여부^{macro state}로 학습의 완성을 구별한다고 했을 때, 학습이 무르익었을 때 첫수의 패턴은 다른 패턴들과 뚜렷하게 구별되는 희귀한 경우^{micro state}이다. 상대적으로 엔트로피가 낮고 높은 정보량을 갖고 있다고 볼 수 있다. 반면에 학습 초기의 첫수 선택의 양상은 거의 무작위이다. 구별할 수 없는 많은 패턴들^{micro state}이 여기에 해당한다. 이는 엔트로피가 높고 정보량이 낮다고 볼 수 있다. 우리가 똑똑하다고, 지능적이라고 일컫는 행동들은 다양한 선택지들에서 망설임 없이 명확한 선택을 일관성 있게 해내는, 즉, 낮은 엔트로피의 패턴이라고 생각된다.

시간에 따라 경험을 쌓아가면서 큐함수에 대한 전체적인 값들이 상승하고 이와 더불어 선택의 기준도 명확해지는 것이 흥미로운데, 필자는 이러한 점에서 강화학습의 과정에서 열역학 실험이 연상된다. 좋은 경험은 시스템의 온도를 높이는 연료 역할을 하게 되고, 시스템이 일정수준의 높은 온도에 올랐을 때 비로소 낮은 엔트로피의 패턴이 탄생하는 것이다.

탐험에서 경험의 다양성을 추구하는 것도 중요하다. 지금까지와는 전혀 다른 경험을 얻고 거기에서 고득점이 가능한지 알아봐야 한다. 이렇게 얻은 양질의 경험을 연료 삼아서 시스템 온도에 해당하는 큐함수의 전반적인 값들이 효율적으로 상승하면, 비로소 매우 낮은 엔트로피의 명확하고 희귀한 패턴이 만들어지는 것이다. (실험 과정에서 이러한 ‘비유’는 시스템의 변수를 설정하고 결과를 해석하는 데 많은 도움이 되었다. 여기에 더 나아가 엄밀한 수학적 물리학적 분석이 필요하다고 생각한다.) 

이렇게 강화학습과정을 이해했을 때, 문제는 결국 학습 효율이다. 문제의 크기가 커질수록 효율의 문제는 더욱 심각해진다. S10.20 심층큐러닝 에이전트가 규칙기반 방법의 성능을 능가하여 14점대의 평균 성능을 보이는 데는 약 두시간이 소요된다. 하지만, S20.30의 경우는 규칙기반의 최고치인 50점대의 성능을 얻는데 약 2일의 학습시간이 소요된다. (시간 측정을 위한 실험은 모두 Nvidia 1080 Ti급의 GPU 기준이다.) 아래에서는 드디어 최종 보스 S20.30에 도전한 이야기를 시작한다.

S20.30

S5.10에서 시작해서 S10.20까지 오면서 에이전트의 최적 정책을 찾는데 여러 가지 시행착오를 겪어야 했다. 하지만 이러한 반복적인 실험은 딥러닝에서는 일상적인 일이다. (크게 어렵지도 않지만, 결코 우아하지도 않다.)

S10.20은 처음에는 하루 정도의 학습시간이 소요되었다. 학습 효율을 높이기 위한 코드 최적화 과정과 수많은 인수 튜닝의 과정을 거치면서 학습은 두 시간 정도로 단축되었다. 하지만 S20.30의 최적정책에 도달하는 것은 결코 만만하지 않았다. 초기에는 2일 넘게 학습해도 목표로 하는 50점의 절반에도 미치지 못했다. 최종적으로 50점대의 성능에 도달했을 때는 1.7일 정도가 걸렸다.

S20.30의 학습 효율을 높이는데 여러 가지 작은 고안들이 필요했지만, 가장 큰 도움을 준 방법은 직관에 의거한 휴리스틱^heuristic 방법이었는데, 이름을 붙이자면 경험의 재활용이고 경험 망각의 문제를 해결하는 데 큰 도움을 주었다.

새롭게 축적한 경험을 반영하기 위해 심층신경망에 저장된 큐함수를 업데이트할 때는 역전파^{back propagation} 방법을 쓰게 된다. 이 과정에서 신경망에 저장된 기존의 경험들이 사라지거나 값이 흐트러지는 경우가 발생하는 것이 일반적이다. (이는 기존의 테이블이나 데이터베이스를 사용하는 방법과 크게 다르다.) 예를 들어, 무작위 탐험으로 얻은 낮은 큐값의 경험들을 기존에 축적한 좋은 큐값의 기억들을 지워가며 기억하게 되는 것이다. 이를 경험 망각의 문제라고 한다.

이런 경험 망각의 문제를 해결하기 위해서 고안한 방법은 간단하다. 기존의 정책을 100% 따라 수확한 경험들과 현재의 탐험율 \(ϵ\)로 수집한 새로운 경험을 1:1로 혼합한 경험을 구성하고, 이를 지도학습 데이터로 삼아 큐함수를 업데이트하는 것이다. 효과는 꽤나 좋았다.

이를 열역학적 실험에 비유하자면, 기존의 시스템 온도를 유지하는 데 필요한 연료와 온도를 상승시키는 데 필요한 연료를 적당한 비율로 함께 섞어 주는 것이 아닐까 생각된다. 연료 혼합의 최적의 비율, 즉 기존 경험과 새로운 경험을 어떤 비율로 섞는 게 좋을지를 매 순간 결정하는 것도 해결해야 할 중요한 문제 중 하나이다.

이 방법을 통해 얻은 첫수의 진화 과정은 다음 그림과 같다. 학습이 진행되면서 대각선이 중앙에서 선명해지는 것을 볼 수 있다.

S20.30의 강화학습에서 발견한 가장 흥미로운 사실은 버퍼 전략의 탄생이다. 이는 위 그래프를 통해서 알 수 있다. S5.10과 S10.20에서 첫수 그래프는 전체를 관통하는 대각선으로 표현된다. 하지만 S20.30의 첫수는 대각선의 모양이지만 양끝을 차지하지 않는다. 즉, 1을 첫수로 배치해야 할 때, 첫 번째 칸에 두지 않고, 앞에 두어 칸을 비워 둔다는 이야기다. 30을 첫수로 배치할 때도 유사하다. 맨 끝에 넣는 대신 끝에서 두어 칸 떨어진 곳에 배치하는 것이다. 이런 식이라면 20칸을 모두 연결한 가장 긴 오름차순은 발생하지 않는다. 왜 이런 전략이 발생했을까?

버퍼 전략은 게임 플레이 과정에서 인접한 칸에 배치하지 못하는 경우, 예를 들어 10과 12가 붙어 있는 상황에서 11을 입력해야 하는 경우를 처리하는 데 큰 도움이 된다. 이런 버퍼 전략은 평균 성적을 최대화하는 방식으로 학습을 했다는 것을 의미한다. 20칸을 모두 오름차순으로 만들어 300점의 최고점을 받는 경우는 아예 고려하지 않는다는 것이다. 물론 탐험 과정에서 수집했을 수도 있지만, 희귀한 케이스이기 때문에 신경망에서는 곧 잊혀졌을 것이다.

사실 규칙기반 방법에는 이미 네 칸의 버퍼 전략을 말판의 한쪽 끝에 적용해서 평균 50점대를 달성할 수 있었다. 규칙기반 방법에 버퍼 전략을 구현한 것은 직관적인 선택이었고 실험적으로 버퍼를 설정했을 때 최고점이 나온 것을 확인한 후의 결정이었다. 이러한 버퍼 전략이 인간의 개입이 전혀 없이 강화학습에서 창발되었다는 사실은 매우 흥미롭다.

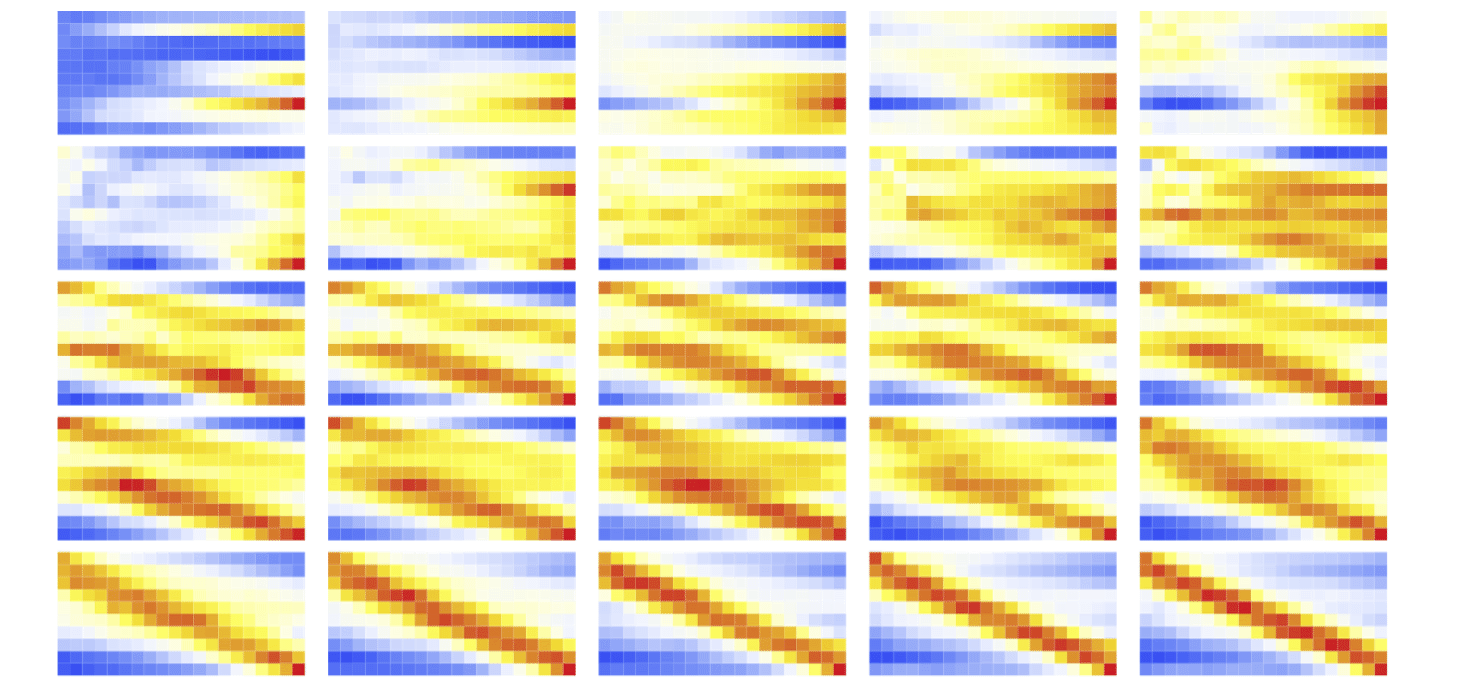
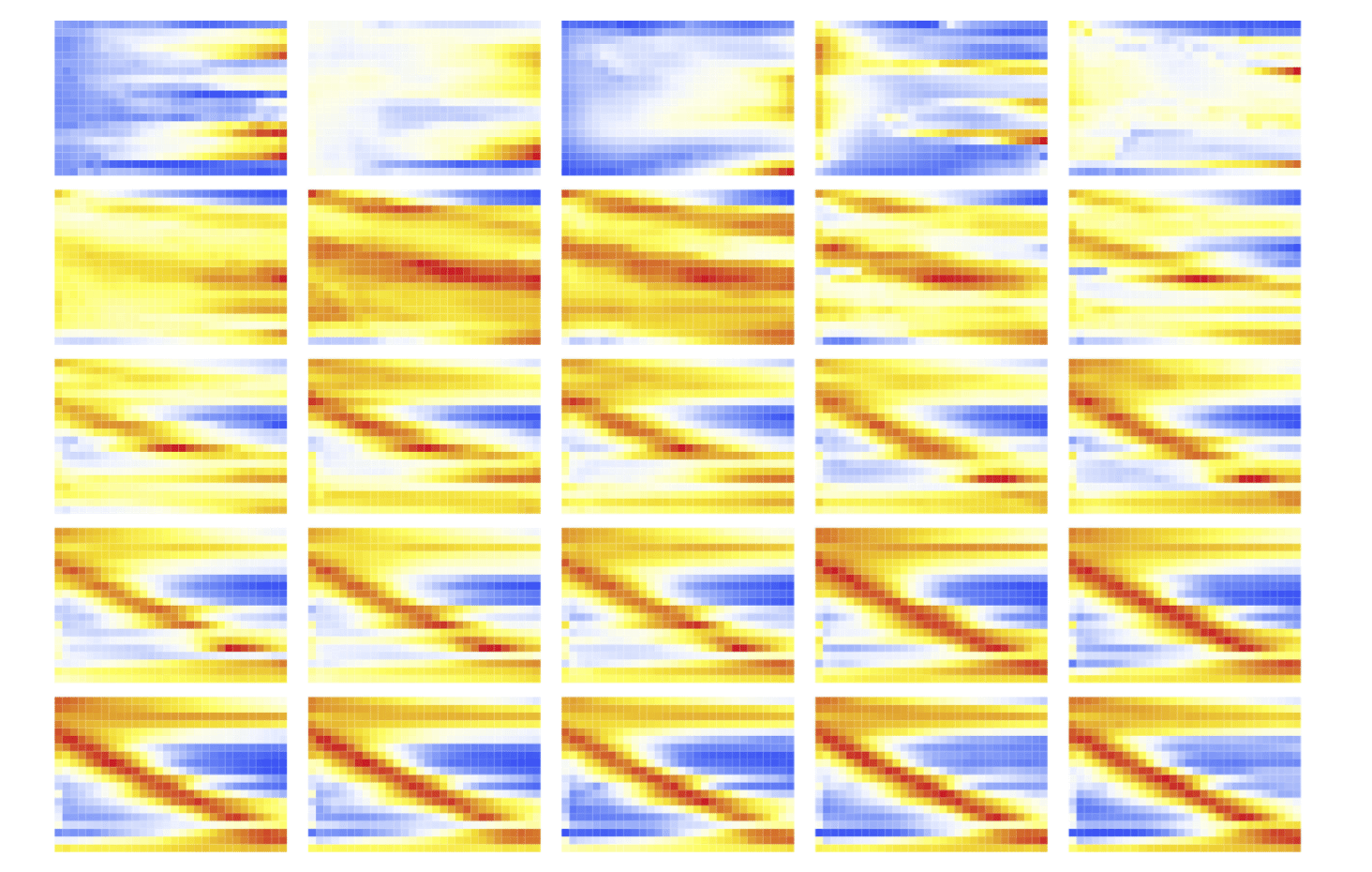
또 한 가지 중요한 고찰은 전체적인 큐값의 상승이다. 아래 그림에서 초기에는 엔트로피가 높고 전체적으로 낮은 큐값의 첫수 선택 패턴을 볼 수 있다. 하지만 시간이 갈수록 전체적인 큐값은 상승하고 이와 더불어 선택의 기준도 명확해져서 엔트로피가 낮은 패턴이 발생함을 볼 수 있다. (위 그래프에서 하나의 선은 1부터 30까지의 숫자 하나에 해당하고, 가로축은 말판의 위치, 세로축은 큐값이다. 즉, 어떤 숫자를 첫수로 넣을 때 말판 각 위치에서의 큐값을 보여준다.)

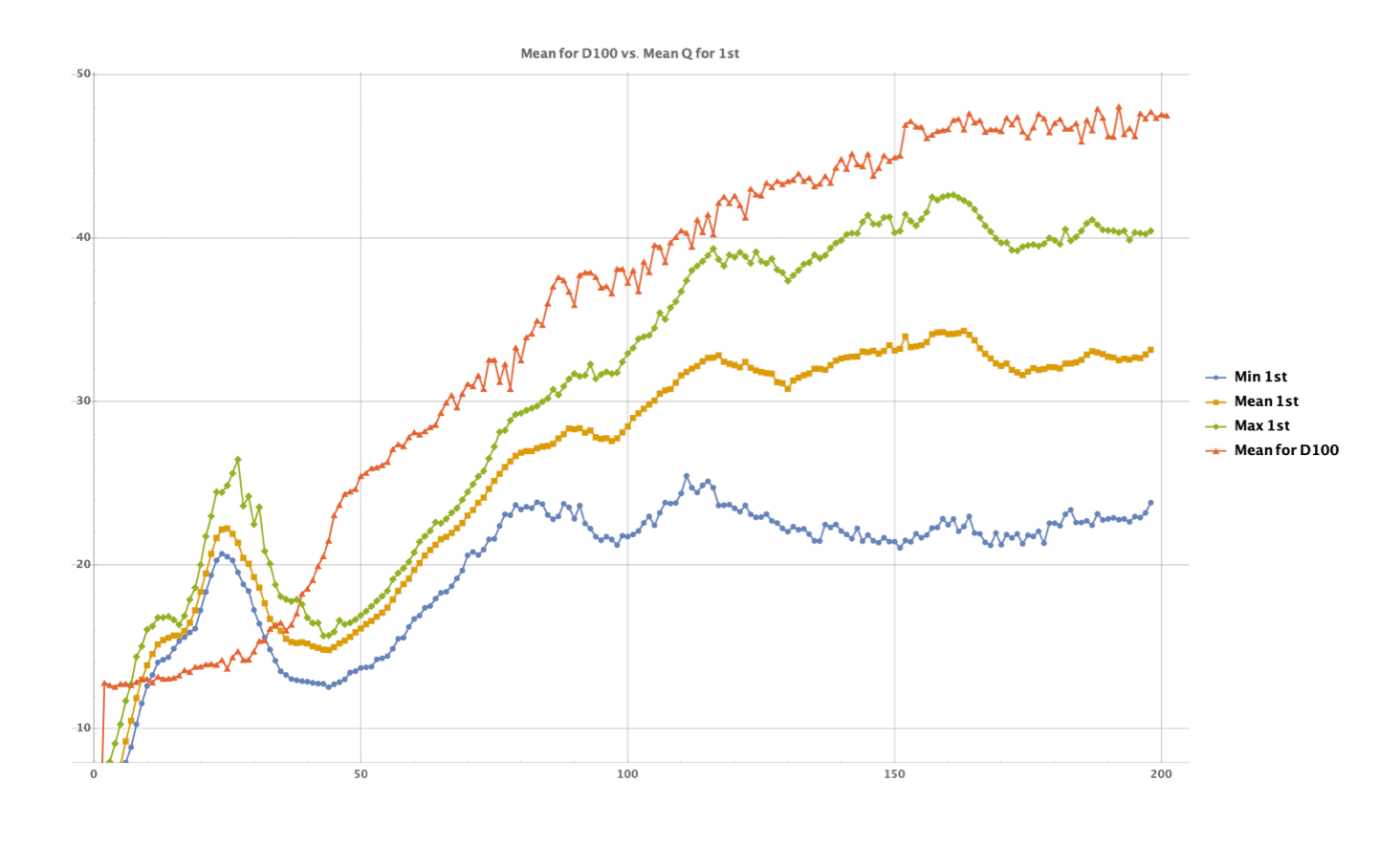
[그림13]의 그래프가 개별 숫자에 대한 그래프였다면, [그림14]의 그래프는 첫수에 대한 평균 큐값과 전체적인 평균 성적의 진화를 볼 수 있다. 첫수에 대한 큐값은 초기에는 무작위 초기화에서 출발하기 때문에 전체적으로 불안하고 비정상적인 값을 갖다가, 초기화 이후 전반적으로 상승하는 것을 볼 수 있다. 또한 감가율(\(γ\))을 적용하여 미래 보상을 모두 신뢰하지 않았기 때문에 첫수의 큐값은 실제 평균 득점보다 낮은 것도 알 수 있다.

[그림15]의 그래프는 점수 분포의 진화,즉 시작에서 학습 종료까지의 점수 분포가 어떻게 변화하는지를 보여준다. 붉은색은 학습이 전혀 되지 않은 초기화 상태의 정책으로 플레이할 때 점수의 분포이다. 정책 없이 무작위로 플레이하는 것과 같다. 평균은 13점 정도이고, 낮은 점수대의 구간에서 정규분포의 형태를 보인다.

하지만 학습을 끝마치고 난 후에는 평균 50점 정도의 푸른색의 분포를 갖게 된다. 전체적으로 점수가 상승하여 높은 점수대까지 이르고 있는 것을 볼 수 있다. 회색은 학습 중간에서의 점수 분포이다.

이상에서 심층강화학습 에이전트가 S20.30을 약 1.7일간 학습하여 평균 50점대의 성능을 낼 수 있었던 과정을 설명하였다. 유사한 성적을 내는 규칙기반의 코딩에 보름 이상이 소요된 것에 비하면 상당히 짧은 시간에 기계가 코드를 만들어 낸 것이다. 최종 학습에 성공하기까지는 훨씬 더 긴 시간과 수많은 GPU 컴퓨팅 자원이 필요했지만, 덕분에 필자의 강화학습 연구도 여러 가지로 발전할 수 있었다.

나가며

이제 스트림스 게임을 통한 강화학습으로의 짧은 여행을 마칠 때가 되었다. 여정을 정리해 보면 다음과 같다. 스트림스 게임은 오름차순 빙고 게임으로 매우 단순한 규칙을 갖고 있지만, 경우의 수가 매우 많아서 이를 스스로 플레이하는 에이전트를 규칙·탐색 기반의 방법으로 작성하기가 생각보다 매우 어렵다는 것을 살펴보았다. 최근 주목받고 있는 강화학습의 원리를 간단히 설명하고, 이를 스트림스 게임에 적용하기 위한 모델과 실제 실험 결과를 소개하였다.

특히, 스트림스 게임 에이전트를 강화학습으로 만드는 과정에서 발견한 재미있는 사실들은 다음과 같다.

1. 사람의 직관과 수작업만으로는 어려웠던 섬세하고 다양한 규칙들을 강화학습의 데이터 기반의 방법으로 찾아낼 수 있었다.
2. 거대한 탐색 공간을 심층신경망기반 큐함수에 효율적으로 저장할 수 있었다.
3. 평균을 최대화하는 과정에서 버퍼 플레이와 같은 묘수를 스스로 찾아내었다.

하지만 최고의 성능에 도착했다고 보기는 이르다. 학습 효율면에서도 해결해야 할 문제들이 가득하다. 아래는 관련해서 독자들에게 드리고 싶은 질문이기도 하다. 

첫 번째는 최신 강화학습기법의 적용이다. 본고에서 적용한 강화학습 기법은 가장 기초적인 심층큐러닝 방법이기 때문에 최근에 연구된 강화학습 기법을 적용한다면 성능과 학습 효율은 많이 개선될 것이라고 생각된다. 최신 기법의 구현을 통해 스트림스 게임 성능 벤치마크를 만들고자 하는데, 여기에 함께 하실 분들의 참여를 환영한다.

두 번째는 열역학적 관점에서 문제를 기술하고 해결하는 것이다. 우선은 이를 비유적으로 기술하였는데, 이를 다시 정리하면 다음과 같다.

1. 관찰된 바에 의하면, 시스템의 온도가 일정 수준 이상 상승해야 엔트로피가 낮은, 즉 지능적인 선택의 패턴이 발생한다.
2. 시스템 온도를 높이기 위해서는 성능 좋은 땔감에 해당하는 양질의 경험들이 필요한데, 이를 효과적으로 수집하고 선별하는 방법이 필요하다.
3. 양질의 땔감은 흔하지 않으며 넓은 경험 축적을 통해서만 구할 수 있다. 넓은 경험은 높은 엔트로피의 패턴을 보여야 한다.
   
   

필자의 열역학에 대한 지식의 한계와 제한된 지면 관계상 더 상세한 기술을 하지는 못했는데, 혹시라도 이 문제에 흥미를 느끼시고 함께 토의하고 조언해 주실 분들은 언제라도 연락을 주시기 바란다.

최근에 딥러닝의 발전을 통해 인류 역사상 최초로 거대한 데이터를 제대로 다룰 수 있는 시대에 접어들었다고 생각한다. 이는 새로운 불을 발견한 것과도 유사한 것 같다. 불에 구운 고기의 맛에 심취해서 너도나도 다양한 실험들을 하고 있지만, 아직 그 불을 완전히 정복하지는 못했다고 생각한다. 거대한 데이터에 기반한 새로운 함수 작성법의 원리를 규명하고 새로운 도구를 정복하는데 물리학자와 수학자들, 그리고 젊은 과학도들의 참여를 권유하는 바이다.

지금까지 스트림스 게임을 통해 강화학습에 입문한 필자의 경험을 여러분들과 공유하였다. 부디 과학의 지평을 넓히는 데 일조했기를 바라는 마음으로 연재를 마친다.