9월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
9월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 김등힐님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
이 문제는 더그 채텀Doug Chatham의 논문 “Reflections on the \(n+k\) dragon kings problem”을 참고하였다. 이 논문은 \(n \times n\) 격자에 \(k\)개의 보병과 \(n+k\)개의 용왕을 배치하는 방법을 다루고 있다. 이번 호의 문제는 \(9+4\) dragon kings problem에 해당하고, 가능한 모든 경우를 다 세어 보면 48374가지 경우가 있다. 이 가운데 90도 회전해서 같아지는 배치를 채텀Chatham은 doubly centrosymmetric solution이라 불렀다.
다음은 90도 돌려도 같아지는 배치이면서 어느 두 용왕도 서로를 공격하지 못하는 한 예이다. 대칭성을 고려하면 아래 예와 다른 풀이가 세 종류 더 존재한다.
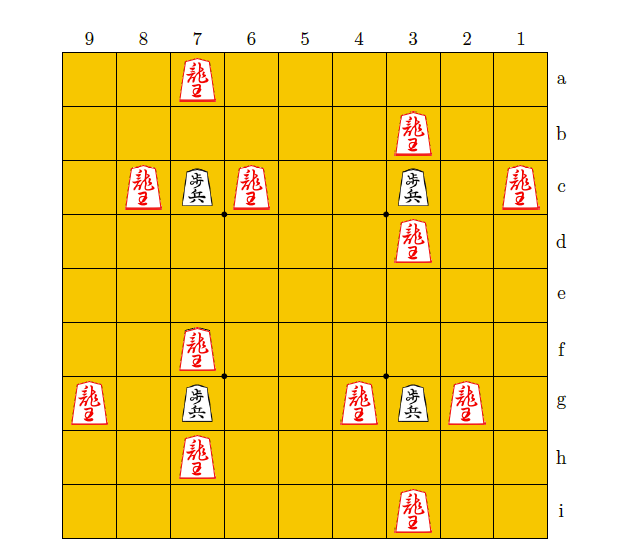
90도 회전 대칭인 경우는 \(9+4\)가 용왕을 배치할 수 있는 최대 개수이며, 90도 회전 대칭이 아닌 경우라면 최대 \(9+5\)개의 용왕을 3540가지 방법으로 배치할 수 있다. 다음은 보병 5개, 용왕 14개를 배치한 것으로, 이 배치는 180도 대칭을 이룬다.
다음은 9월의 정답자로 선정된 김등힐님의 해설입니다.




