10월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
10월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 김운기님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
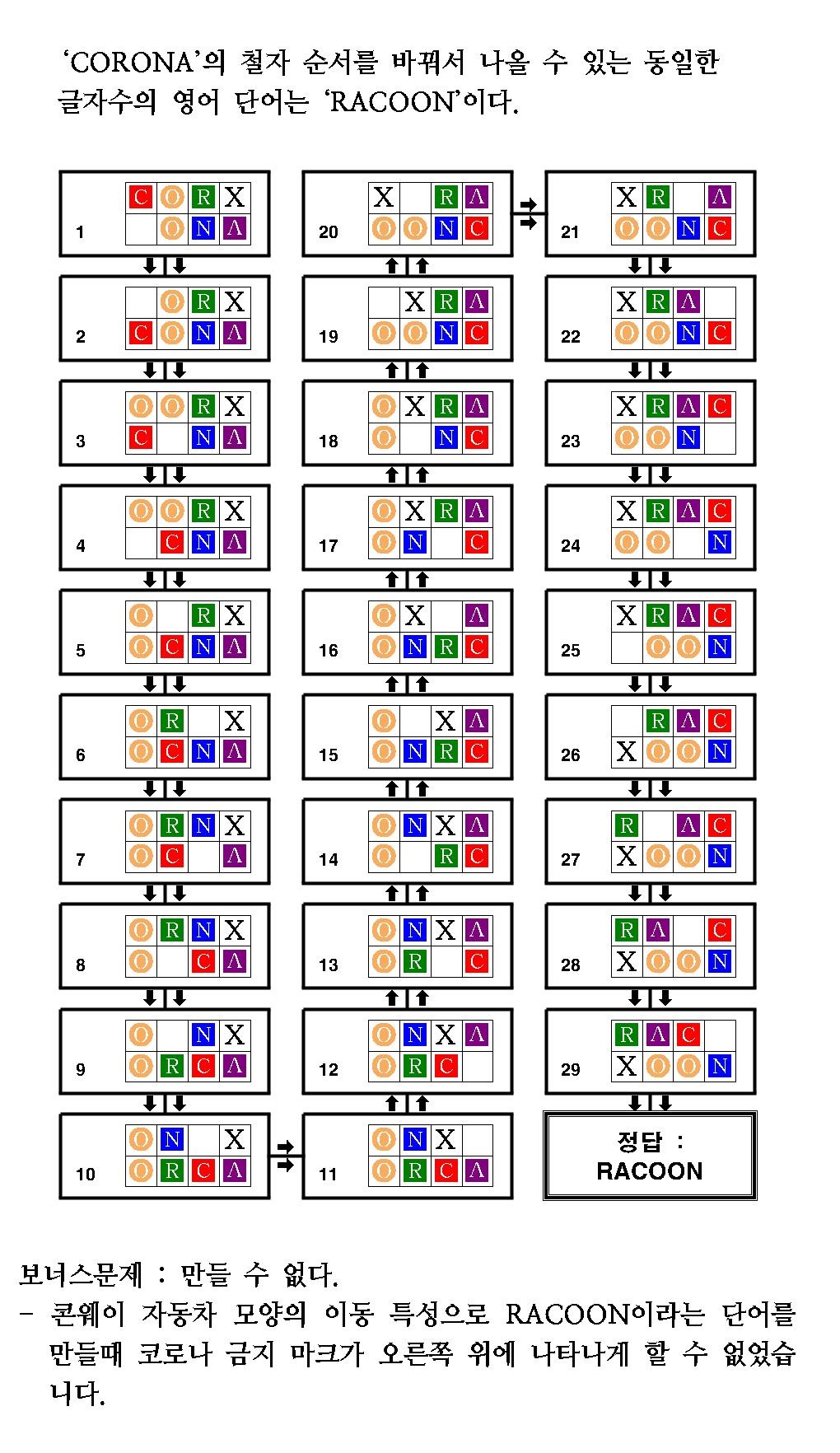
차례대로 다음과 같이 움직이면 28단계만에 RACOON을 만들 수 있다.
O(회전) – R – N – A – X – N – A – O(이동) – C – R – A – O(회전) – C – R – A – O(회전) – X – N – O(이동) – C – X – O(회전) – N – O(회전) – C – A – R – X – O(이동) – N
이해하기 쉽게 움직이는 그림으로 나타내면 다음과 같다.
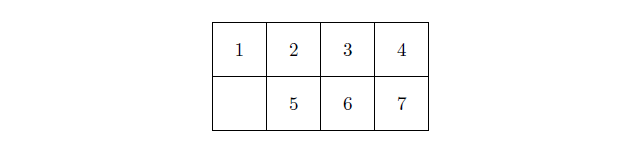
보너스 문제로 제시한, RACOON을 만들면서 코로나 금지 마크가 오른쪽 위로 오게 만드는 것은 불가능하다. 각각의 조각에 다음과 같이 차례대로 번호를 붙였다고 생각하자.

이제 위 줄 왼쪽에서 오른쪽으로, 다시 아래 줄 왼쪽에서 오른쪽으로 순서를 정하여, 각 수마다 자기보다 앞에 오면서 자기보다 큰 수를 세어 본다. 이 개수를 각 수의 반전수inversion라 한다. 지금은 모든 수가 크기 순으로 놓여 있으므로, 반전수는 모두 0이다. 이제 이 반전수들의 합에 빈칸이 있는 행의 번호를 더한다. 지금은 반전수는 모두 0이고 빈칸이 있는 행은 2이므로, 계산 결과는 짝수가 된다.
조각 하나를 움직일 때 반전수가 어떻게 변하는지 살펴보면, 가로로 조각을 움직이면 반전수가 변하지 않는다. 반전수는 아래 위로 조각이 움직일 때만 변한다. 예를 들어, 위의 배치에서 1번 조각을 아래로 내리면 다음과 같은 배치가 되고, 다른 수의 반전수는 여전히 0이지만, 1 앞에는 2, 3, 4가 있으므로 1의 반전수는 3이 된다. 그러면 각각의 반전수를 더하고 빈칸이 있는 행의 번호 1을 더한 결과는 3+1이 되어 역시 짝수가 된다.
이와 같이, 조각을 어떻게 움직이더라도 반전수의 합에 빈칸이 있는 행의 번호를 더한 같은 항상 짝수이다. 이것을 이 퍼즐의 불변량invariant이라 한다. 즉, 배치가 바뀌어도 변하는 않는 성질이다.
우리가 원하는 최종 상황은 4번 조각이 제자리를 지킨 다음 두 가지 배치라 할 수 있다.
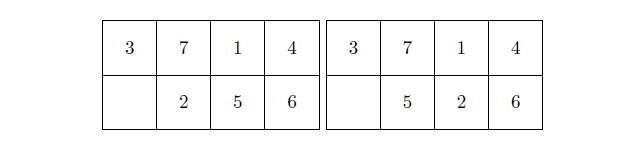
2번과 5번은 똑같은 알파벳 O로 구별이 되지 않으므로 위의 두 가지 상황이 가능하다. 그런데 불변량을 구해 보면, 첫 번째 배치는 반전수의 합
\[
0+0+2+1+3+1+1 = 8
\]
에 빈칸이 있는 행의 번호 2를 더한 값이 짝수이지만, 두 번째 배치는 반전수의 합
\[
0+0+2+1+1+4+1 = 9
\]
에 빈칸이 있는 행의 번호 2를 더한 값이 홀수가 된다. 조각을 어떻게 움직여도 불변량은 짝수여야 하므로 두 번째 배치는 불가능함을 알 수 있다.
이 결과로부터, 보너스 문제를 해결하려면 처음에 세로로 놓여 있던 2와 5를 움직여서, 두 번째 행에 2, 5 순서로 놓이도록 배치해야 한다. 그런데 처음에는 2가 위, 5가 아래에 있었고, 이 세로 조각의 왼쪽에 빈칸이 있었으므로, 2-5 조각을 두 번째 행에 가로로 놓으면 반드시 5, 2 순서가 된다. 이 상황에서 조각들을 움직여 첫 번째 행에 빈칸을 만들었다고 생각해 보자. 두 번째 행에 5, 2 순서로 놓인 2-5 조각을 세로로 옮기면, 2번이 위로 가는 경우에는 5번이 있던 자리에 빈칸이 생기고, 5번이 위로 가는 경우에는 2번이 있던 자리에 빈칸이 생긴다.
2-5 조각을 움직여 2번이 위로 가게 한 경우, 왼쪽에 빈칸이 생기므로, 조각을 어떻게 움직이더라도 2-5 조각을 다시 두 번째 행으로 옮기는 순간 5, 2 순서가 된다. 한편, 2-5 조각을 움직여 5번이 위로 가게 한 경우, 오른쪽에 빈칸이 생기므로 이번에는 2-5 조각을 두 번째 행으로 옮기는 순간 다시 5, 2 순서가 된다. 따라서 2-5 조각을 두 번째 행에 2, 5 순서로 놓을 수가 없으므로, 아무리 움직여도 보너스 문제에서 제시한 상황은 만들 수 없다.
만약 두 O가 분리되어 있다면 보너스 문제도 해결할 수 있다. 이 경우 조각을 24번 움직여서 원하는 배치를 만들 수 있다.
다음은 10월의 정답자로 선정된 김운기님의 해설입니다.