3월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
3월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 안진후님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
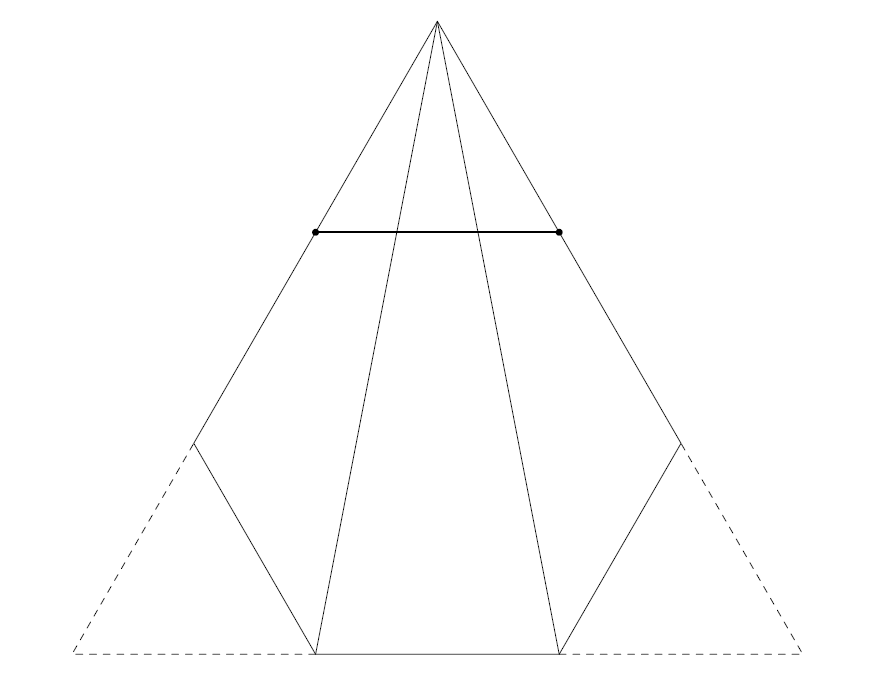
다음과 같이 선분의 아래위로 정삼각형과 정육각형을 그리면 선분을 삼등분할 수 있다.

이 방법이 선분을 삼등분한다는 것은 다음 그림과 같이 보조선을 그려 보면 알 수 있다.
다음은 3월의 정답자로 선정된 안진후님의 해설입니다.
어떤 3 이상의 자연수 n에 대해서도 정2n각형 하나만 그리면 주어진 선분을 삼등분 할 수 있다.
작도법:
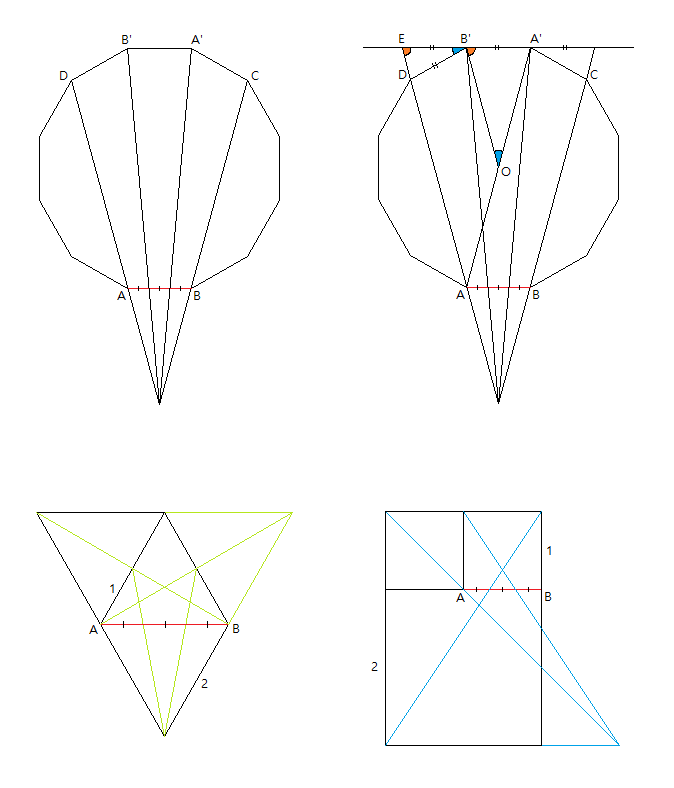
1. 주어진 선분을 AB라 할 때, AB를 한 변으로 갖는 정2n각형을 작도한다. 여기서 정2n각형의 중심 O에 대해 A의 대칭점을 A’, B의 대칭점을 B’이라 칭하자. 그리고 A’과 정2n각형의 한 변을 이루면서 B’이 아닌 점을 C, B’과 정2n각형의 한 변을 이루면서 A’이 아닌 점을 D라 하자.
2. 직선 AD, BC를 그어 그 교점 X를 찾는다.
3. 직선 A’X와 B’X를 그어 선분 AB와의 교점을 찾으면 바로 AB의 삼등분점이 된다.
증명:
B’A’의 연장선과 직선 AD의 교점을 E라 하자. B’A’과 AB가 평행하므로 증명은 EB’=A’B’을 보이는 것으로 충분하다.
1) 정다각형의 대칭성의 의해 직선 AD와 직선BB'(=직선 OB’)은 평행하다. 따라서 각DEB’=각BB’A’(=각OB’A’)
2) 각EB’D는 정2n각형의 외각이므로 그 크기가 360/2n이고 각A’OB’역시 정다각형의 성질에 의해 그 크기가 360/2n이므로 각EB’D=각A’OB’
3) 1)과 2)에 의해 삼각형EDB’과 삼각형 A’B’O는 닮음이다. 삼각형 A’B’O가 이등변 삼각형이므로 삼각형 EDB’도 이등변삼각형이고, 따라서 EB’=DB’=B’A’. 증명끝.
이외에서 정삼각형 3개 혹은 정사각형 3개를 그리면 주어진 선분을 3등분 할 수 있다. (길이비가 1:2인 선분들을 찾으면 쉽게 보일 수 있다.)