[6월의 퍼즐 해설] 주사위로 만든 주사위

이 문제는 영국의 잡지 <New Scientist> 2013년 9월 2일에 연재된 퍼즐 코너 “Enigma”의 1768번 문제였다. 출제자는 수전 데넘^{Susan Denham}이었다. 원제는 “Die hard”. 주사위를 영어로 die라고 하는 사실을 이용한 말장난이었다.

큰 주사위의 각 면은 작은 주사위의 면 네 개로 이루어지므로, 큰 주사위의 각 면에 나타나는 점은 4개 이상 24개 이하이다. 이 범위에서 제곱수는 4, 9, 16이 확정되고 소수는 2, 3, 5, 7, 11, 13, 17, 19, 23 가운데 세 개를 골라야 한다.

4와 16이 각각 소수와 마주 본다면, 마주 보는 두 면의 합이 홀수가 되어야 하고, 그러면 9와 마주 보는 면이 2일 수밖에 없는데, 이렇게 되면 합이 11이 되어 16의 짝이 없으므로 불가능하다.

4와 9가 마주 본다면 합이 16보다 작으므로 역시 불가능하고, 9와 16이 마주 보는 경우는 4와 21이 짝을 이루어야 하는데 21은 소수가 아니므로 역시 불가능하다.

따라서 4와 16이 서로 마주 볼 수밖에 없으므로, 4-16, 9-11이 서로 짝을 이루고, 소수로는 7-13이 짝을 이룬다. 즉, 큰 주사위의 마주 보는 면의 합은 20이다.

큰 주사위 전체로 보면 겉에 드러난 점은 \(20 \times 3 = 60\)개이다. 작은 주사위의 4가 모두 안으로 숨어 있다는 것은 마주 보는 면인 3이 모두 겉으로 드러나 있다는 뜻이 된다. 큰 주사위의 점 60개 가운데 \(3 \times 8 = 24\)개를 제외한 36개를 3이 아닌 수, 즉, 1, 2, 5, 6의 합으로 나타낼 수 있어야 한다. 작은 주사위는 모두 여덟 개이고, 1-6, 2-5는 서로 마주 보는 면이므로, 겉으로 드러난 1이 \(x\)개이고 2가 \(y\)개라면 6은 \(8-x\)개, 5는 \(8-y\)개가 드러난다. 그러면 \(x\)와 \(y\)는

\[
1x+2y+5(8-y)+6(8-x) = 36, \quad
0 \le x, y \le 8
\]
라는 조건을 충족해야 한다. 이 방정식은 \(x=8, y=4\)가 유일한 정수해이므로, 다음과 같은 결과를 얻는다.

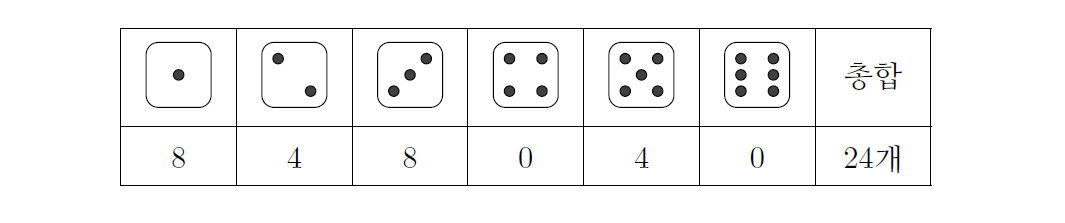
깔끔한 풀이기는 하지만 이 방법의 문제점은 실제로 이러한 주사위를 구성할 수 있는지는 알 수 없다는 점이다. 이제 실제로 큰 주사위를 어떻게 구성할 수 있는지 알아보자.

주사위 네 면의 합이 4가 되는 경우는 네 주사위가 모두 1인 \((1,1,1,1)\)밖에 없다. 편의상 큰 주사위의 각 면을 면4, 면7, 면9, 면11, 면13, 면16으로 부르자.

면7을 구성할 수 있는 경우를 찾아보면, 4는 사용할 수 없으므로,

\[
(1,1,2,3),\quad
(1,2,2,2)
\]
의 두 가지가 가능하다.

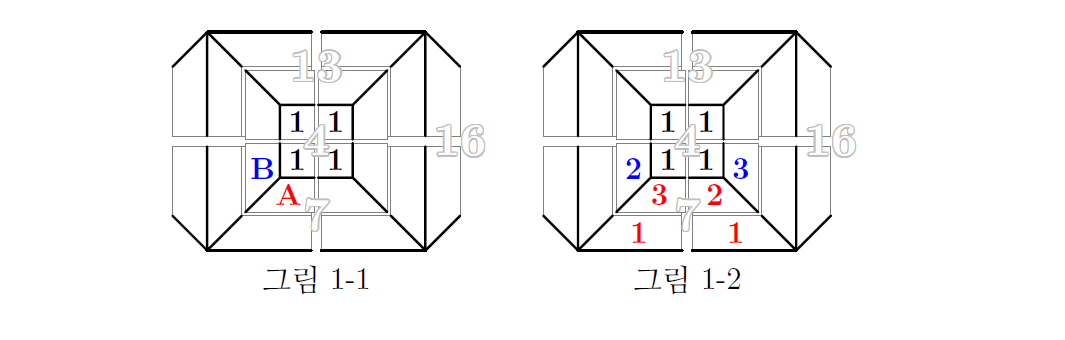
면4를 윗면으로 하고 면7을 앞면에 배치해 보면, 다음 그림 1-1에서 A 자리에는 2가 올 수 없다. 만약 A에 2가 오면, 작은 주사위가 오른손잡이 주사위이므로 B 자리에 4가 나타나기 때문이다. 따라서 앞면이 7이 되는 것은 다음 그림 1-2뿐이다. 양쪽 옆면의 2와 3은 자동으로 결정된다.

면9를 구성하는 방법은

\[
(1,1,1,6), \quad
(1,1,2,5), \quad
(1,2,3,3), \quad
(2,2,2,3)
\]
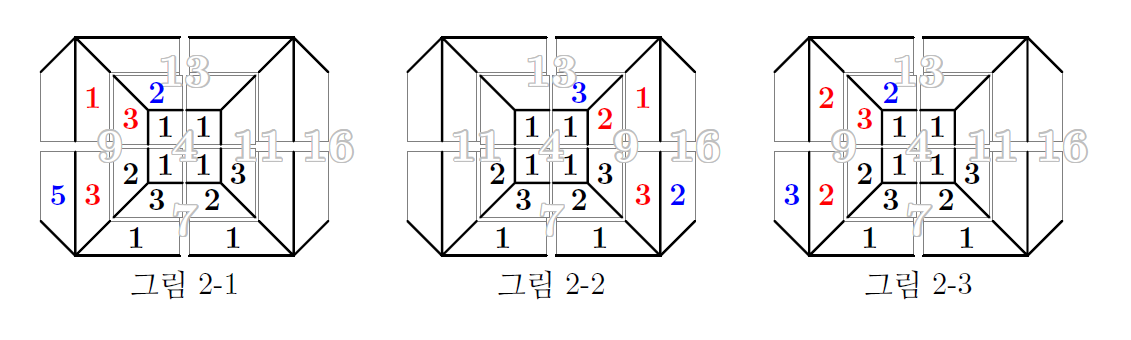
의 네 가지가 가능한데, 이미 1을 여섯 개 사용하였으므로 1이 세 개 더 필요한 첫 번째 경우는 불가능하다. 또, 위의 그림에서 이미 자리 잡은 1과 다른 주사위가 되는 칸이 하나뿐이므로 1 두 개를 배치하는 것도 불가능하다. 따라서 합이 9가 되는 경우는 \((1,2,3,3)\)과 \((2,2,2,3)\)뿐이다. 4가 겉에 드러나지 않도록 이 수들을 배치하는 방법은 다음 세 가지가 가능하다.

합이 11이 되는 경우는

\[
(1,1,3,6), \quad
(1,2,2,6), \quad
(1,2,3,5), \quad
(2,2,2,5), \quad
(2,3,3,3)
\]
의 다섯 가지 경우가 있다.

먼저 면9를 \((1,2,3,3)\)으로 만든 그림 2-1과 2-2를 생각하자. 이 배치에는 1이 일곱 개 사용되었고, 이때 쓰인 주사위는 반대쪽 면에 6이 있으므로, 추가로 사용할 수 있는 1은 하나뿐이고, 1과 6을 동시에 사용할 수도 없다. 따라서 합이 11이 되는 경우는 다음 세 가지뿐이다.

\[
(1,2,3,5), \quad
(2,2,2,5), \quad
(2,3,3,3)
\]
위의 그림 2-1에 각 경우를 배치해 보면, 다음 세 가지가 가능하다.

4가 없고 1과 6이 많아야 하나뿐이면서 합이 13이 되는 경우를 구하면

\[
(1,2,5,5), \quad
(2,2,3,6), \quad
(2,3,3,5)
\]
의 세 가지이다.

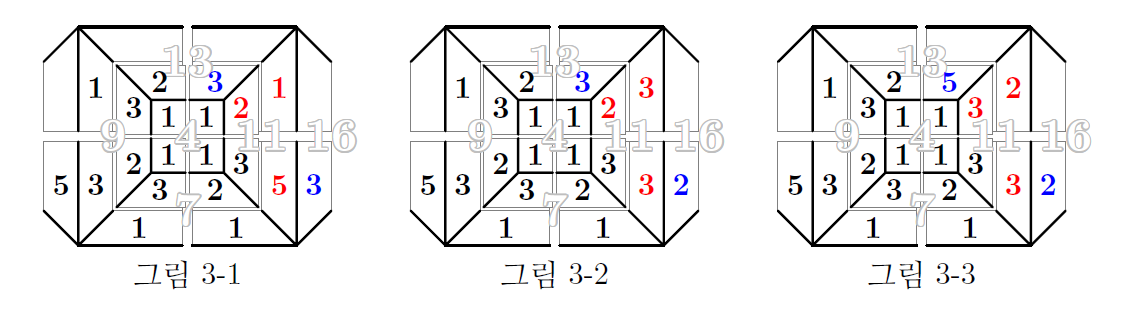
그림 3-1은 2와 5가 합쳐서 이미 여섯 번 사용되었으므로, 여기에 \((1,2,5,5)\)를 배치할 수는 없다. 또, 면13에 남은 두 자리 양쪽에 1이 있으므로, 빈자리 어디에도 \((2,2,3,6)\)의 6을 쓸 수가 없다. 따라서 그림 3-1에 배치할 수 있는 것은 \((2,3,3,5)\)뿐이다. 바닥에 4가 나오지 않으려면 다음과 같이 배치할 수밖에 없고, 이 배치는 모든 조건을 충족한다.

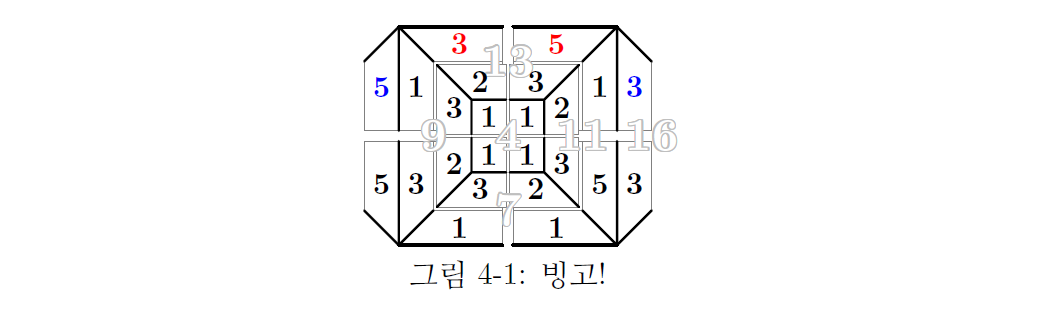
그림 3-2도 2와 5가 합쳐서 여섯 번 사용되었으므로 여기에도 \((1,2,5,5)\)를 배치할 수 없다. \((2,2,3,6)\)을 배치하면 다음 그림처럼 바닥면의 합이 16이 되지 않으므로 이 배치도 불가능하다.

또, 그림 3-2는 이미 3을 일곱 번 사용하였으므로, \((2,3,3,5)\)를 배치할 수도 없다.

이제 그림 3-3의 경우를 생각해 보자. 이때 2와 5가 합쳐서 이미 일곱 번 사용되었으므로, 합이 13이 되는 세 경우 모두 배치할 수 없다.

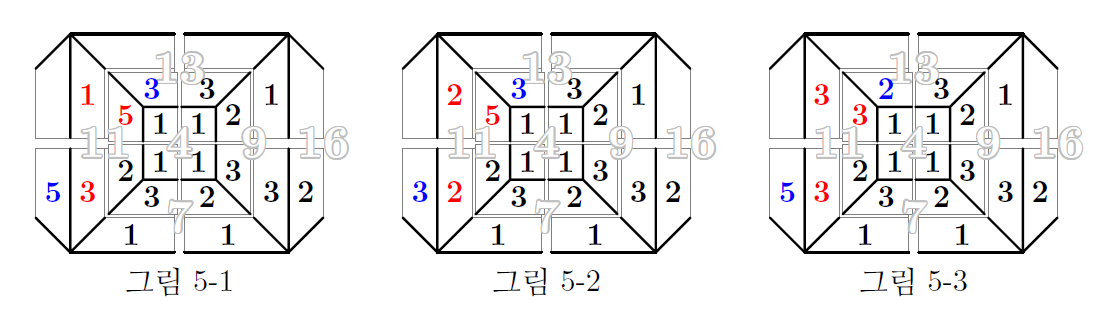
다음으로 그림 2-2에서 합이 11이 되는 경우를 채워 보자. 4가 드러나지 않도록 \((1,2,3,5)\), \((2,2,2,5)\), \((2,3,3,3)\)을 채우면 다음과 같다.

그림 5-1에서 면16의 빈자리 두 수는 합이 9가 되어야 한다. 이것은 3과 6만 가능한데, 두 개의 빈자리 모두 이웃한 면에 1이 있으므로 두 자리 어디에도 6을 쓸 수 없다. 따라서 그림 5-1에 나머지 수를 채우는 것은 불가능하다.

그림 5-2에서 면13을 채우려면 합이 7이 되는 두 수를 사용해야 하는데, 1과 6은 1과 이웃한 자리를 채울 수 없으므로 쓸 수 없다. 또, 2와 5는 2와 이웃한 자리를 채울 수 없으므로 역시 배치가 불가능하다.

그림 5-3에서 면16은 3과 6으로 채워야 한다. 1과 이웃한 칸은 6을 채울 수 없으므로 다음 그림과 같은 배치만 가능하다. 이때 13면에는 \((2,2,3,5)\)가 채워지는데 네 수의 합이 13이 되지 않으므로 이런 배치도 불가능하다.


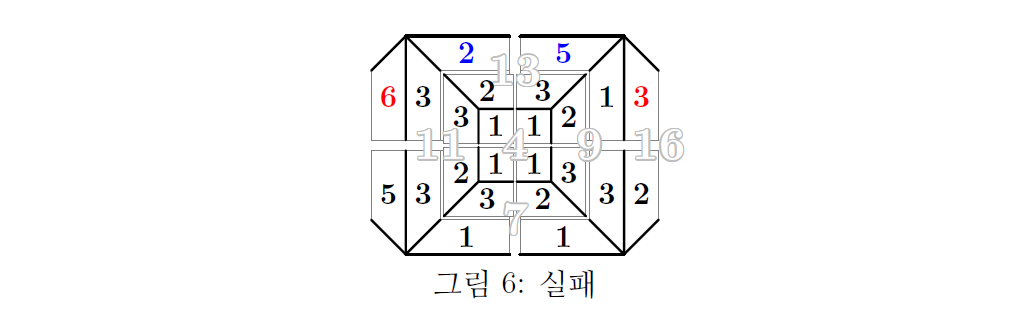
마지막으로 그림 2-3에 면11을 배치하는 경우를 생각하자. 합이 11이 되는 경우는

\[
(1,1,3,6), \quad
(1,2,2,6), \quad
(1,2,3,5), \quad
(2,2,2,5), \quad
(2,3,3,3)
\]
의 다섯 가지 경우가 있었다.

여기서는 면11에 1을 배치할 수 있는 자리가 하나뿐이고 3이 하나 사용되었으므로, 다음과 같이 \((1,2,3,5)\)와 \((2,3,3,3)\)을 배치할 수 있다.

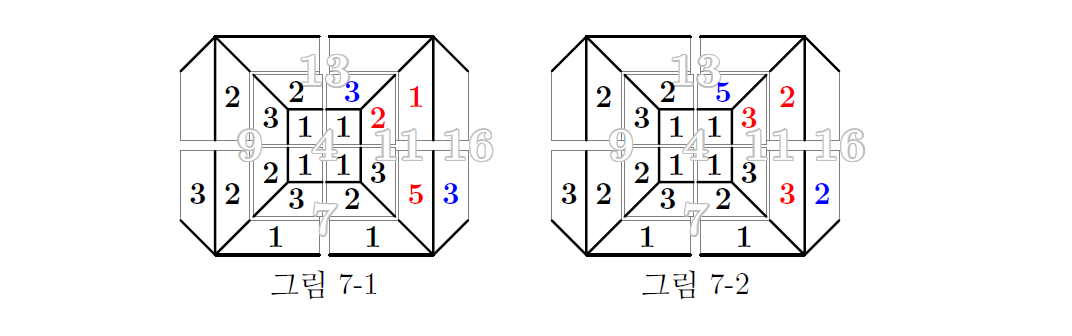
그림 7-1에서 면16의 비어있는 두 자리는 모두 5를 채울 수밖에 없다. 그런데 이미 2와 5를 합쳐 일곱 개를 사용하였으므로 이것은 불가능하다.

그림 7-2에서는 면16의 비어있는 두 자리에 5와 6을 채울 수밖에 없는데, 어느 자리도 2와 이웃한 면이므로 5를 채울 수는 없다.

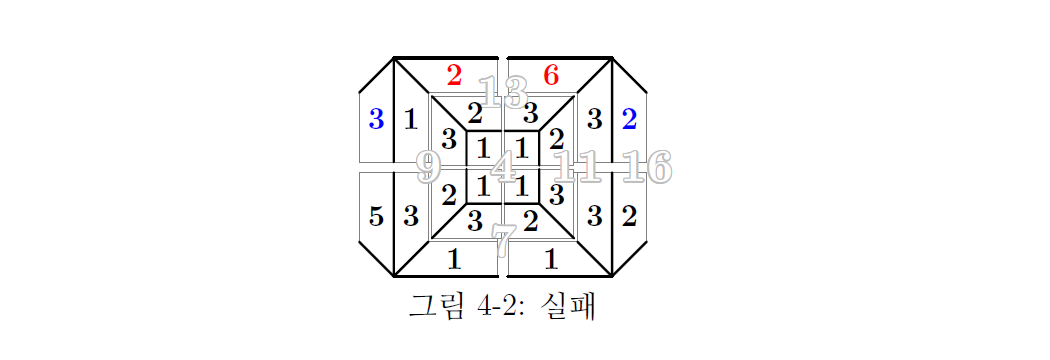
이상의 결과로부터 그림 4-1이 유일한 배치 방법이 된다.