7월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
7월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 정경훈님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
ORION과 ION을 7로 나눈 나머지가 같으므로, 두 수의 차이인 OR\(\times 1000\)은 7의 배수가 되어야 한다. 따라서 두 자릿수 OR도 7의 배수이다.
HORIZON이 가장 큰 값을 가지는 경우로 H가 9인
\(\mathrm{9ORIZON}\)
을 생각하자. 그러면 여기서 7의 배수인 OR를 제거한 결과가 900IZON이고 9000000을 7로 나눈 나머지가 2이므로, HORIZON을 7로 나눈 나머지는
\(2+\mathrm{IZON}\)
을 7로 나눈 나머지와 같다. 이것은 IRON을 7로 나눈 나머지와도 같으므로, 두 수의 차이를 계산하면
\(2+(\mathrm{Z}-\mathrm{R})\times100\)
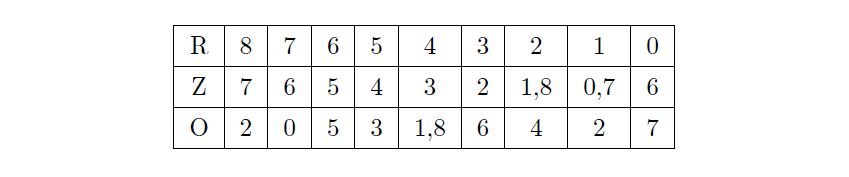
이 7의 배수가 되어야 한다. 100을 7로 나눈 나머지가 2이므로, 이런 일은 \(\mathrm{Z}-\mathrm{R}\)가 6이거나 \(\mathrm{R}-\mathrm{Z}\)가 \(1\)일 때 가능하다. 즉, R와 Z의 값은 다음과 같은 쌍이 가능하다. OR가 7의 배수이므로, 각각의 R에 대해 가능한 O도 함께 표시하였다.
\((9\times\mathrm{I}+\mathrm{R})\times100\)
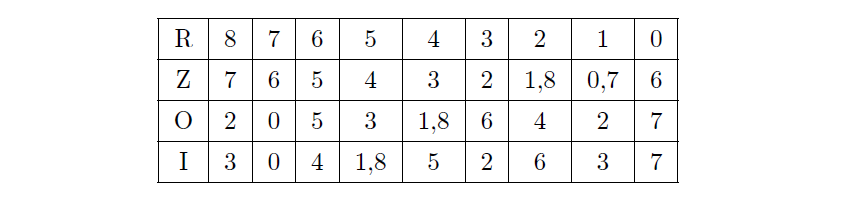
이고 이 값이 7의 배수가 되어야 하므로, \(2\times\mathrm{I}+\mathrm{R}\)가 7의 배수가 되어야 한다. 위의 표에 I에 해당하는 값을 덧붙이면 다음과 같다.
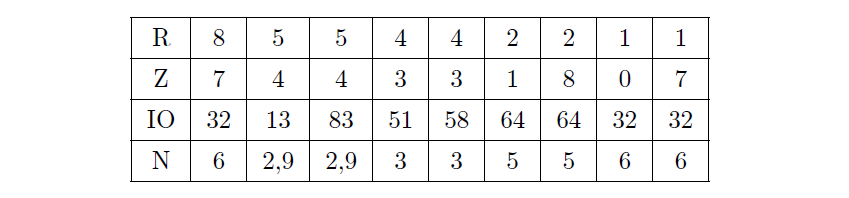
이제 \(\mathrm{ION}-\mathrm{IO} = 9\times\mathrm{IO}+\mathrm{N}\)이 7의 배수가 되는 경우를 생각하여 위의 표에 덧붙이면 다음과 같다. 위의 표에서 숫자가 중복되는 경우는 제외하였다.
HORIZON에서 H를 9로 두었으므로, 이 수가 가장 큰 값이 되는 것은 IO=64일 때이고, 식을 정리하면
\(\mathrm{HORIZON = 9426845}\)
가 가장 큰 값이다. 이때 다섯 개의 수를 7로 나눈 나머지는 1이다.
크기를 생각하지 않는다면 HORIZON으로 가능한 값은 다음과 같이 모두 46가지이다.
\(1283426, 1564258, 1564958, 1845083, 1845783, 1983496, \\
2351439, 2358439, 2496145, 2496845, 2913096, 2913796, 2983096, 2983796, \\
3564158, 3564851, \\
5213926, 5283926, 5913296, 5983296, \\
6145813, 6351239, 6351932, 6358239, 6358932, 6845183, \\
7213826, 7283126, 7426945, 7496245, 7913896, 7983196, \\
8145013, 8145713, 8213426, 8564251, 8564951, 8913496, \\
9213026, 9213726, 9283026, 9283726, 9351432, 9358432, 9426145, 9426845\)
다음은 7월의 정답자로 선정된 정경훈님의 해설입니다.
편의상 모든 합동식에서 (mod 7)은 생략한다.
“HORIZON” ≡ “ORION” ≡ “IO” ≡ “ION” ≡ “IRON” 을 정리하면 다음 식을 얻는다:
R ≡ 4O
I ≡ 5O
Z ≡ 3(H – O)
N ≡ 3O
관계식 사이에 cycle이 없으므로 H와 O에 해당하는 숫자를 먼저 정하면 나머지 자릿수가 모순 없이 정해지게 된다. 다만 서로 다른 알파벳에 같은 숫자가 할당되는 경우를 피해야 된다.
H = 9, O = 8 인 경우부터 “HORIZON”을 크게 만드는 순서대로 하나하나 확인해보면 다음과 같이 답을 구할 수 있다.
H = 9, O = 8: “HORIZON” = 9845383. Z = N = 3 이므로 배제.
H = 9, O = 7: O ≡ R ≡ I ≡ N ≡ 0 이 되어 {0, 7} 중 적어도 하나가 중복이 생기므로 배제.
H = 9, O = 6: “HORIZON” = 9632964. H ≡ I ≡ Z ≡ 2 가 되어 {2, 9} 중 적어도 하나가 중복이 생기므로 배제.
H = 9, O = 5: “HORIZON” = 9564551. O = Z = 5 이므로 배제.
H = 9, O = 4: “HORIZON” = 9426845. 숫자가 겹치는 알파벳 없음.
따라서 조건을 만족하면서 “HORIZON”이 가질 수 있는 가장 큰 값은 9426845이고, 이 때
“HORIZON” = 9426845
“ORION” = 42645
“IO” = 64
“ION” = 645
“IRON” = 6245
의 각각을 7로 나눈 나머지는 모두 1이다.