[12월의 퍼즐] 마법 육각형 위의 동전

100년도 더 전인 1910년 미국. 19살이던 클리포드 애덤스^{Clifford Adamas}는 신문에서 흥미로운 문제를 보았다. 다음 그림처럼 정육각형 19개를 벌집 모양으로 배열하면, 가로 방향과 대각선 방향으로 나란히 다섯 개씩, 정육각형이 맞붙어 만들어지는 줄이 총 15개가 있다. 1부터 19까지의 자연수를 정육각형에 넣어서, 15개의 줄 각각을 더한 값이 모두 같게 할 수 있을까?

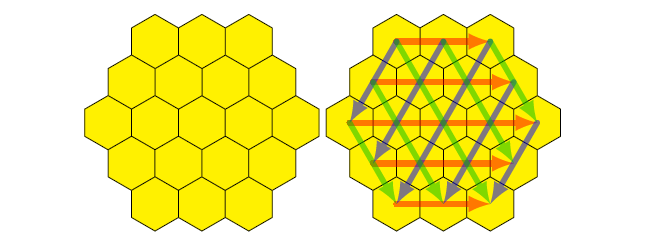
이것은 일종의 마방진인데, 애덤스가 보았던 신문에는, 조판 과정의 오류였는지, 합이 35인 경우를 찾는 것으로 되어 있어서 답이 없었다. 애덤스는 이 합이 \((1+2+\dots+19)/5 = 38\)이라는 것은 금방 알았지만 이 마법육각형의 답을 바로 찾지는 못하였다.

세월이 흘러 1957년. 수술을 받고 회복 중이던 애덤스는 병실에서 이 문제의 답을 찾았다. 무려 47년이 걸린 답안이었다. 그러나 답을 적어 놓은 종이를 잃어 버려서 1962년이 되어서야 다시 답을 찾을 수 있었다.

애덤스는 당시 인기 있던 수학 칼럼 “Mathematical Games”을 연재하고 있던 마틴 가드너^{Martin Gardner}에게 이 답안을 보냈다. 가드너는 이 풀이가 유일한지를 수학자 찰스 트리그에게 문의하였고, 트리그는 1부터 연속한 자연수를 채워서 이런 일이 가능한 경우는 이 배열이 유일하다는 사실을 밝혀내었다.

문제 자체는 간단하기에 이 문제를 독립적으로 만들어낸 사람은 여럿이었으나, 이후 연구를 통해, 현재 이 문제의 최초 출처는 1887년에 독일의 건축가 에른스트 폰 하젤베르크로 알려져 있다.

이제 이 문제를 조금 다르게 다루어 보자. 위의 마법육각형에 숫자를 채우는 대신, 동전들을 정육각형 한 칸에 하나씩 놓아, 15개의 줄에 놓인 금액의 합이 같게 만들 수 있을까?

우리나라에서 사용하고 있는 10원, 50원, 100원, 500원 동전으로는 이렇게 만드는 것이 불가능하다. 그러면, 동전이라는 특성을 이용하여, 딱 한 칸에는 동전 두 개를 겹쳐 놓을 수 있다고 하면 어떨까?

이것 또한 불가능하다. 그러면, 동전을 바꾸어, 미국에서 사용하는 1센트, 5센트, 10센트, 25센트의 네 종류의 동전으로 문제를 풀어보자. 50센트와 1달러 동전도 없지는 않으나 널리 쓰이지는 않으니 앞서 말한 네 종류의 동전을 각 칸에 하나씩 놓되, 딱 하나의 칸에는 동전 두 개를 겹쳐 놓을 수 있다. 이렇게 하여 가로와 대각선 방향인 15개의 줄에 놓인 동전의 금액이 모두 같게 만들려면 어떻게 놓아야 할까?

***

연재 종료 인사

2018년 1월 고등과학원의 웹진 HORIZON 창간과 함께 퍼즐 연재를 시작하여 2021년 12월까지 48회에 이르렀습니다. 훌륭한 필자들의 놀랍고 흥미로운 글들에 비해, 때로는 시시하기도 하고 때로는 유치하기도 한 퍼즐을 게재하려니 부끄럽기도 했습니다. 좀더 멋지고 재미있는 문제들을 만들고 찾아내었어야 하는데, 의욕만 앞서고 성과는 미미했던 것 같습니다.

이제 저보다 훨씬 뛰어난 분들에게 퍼즐 연재를 맡기고, 저는 구경꾼으로 물러나겠습니다. 지난 4년 동안의 성원에 감사드립니다.

* 2022년 1월부터는 새로운 필자분들이 HORIZON 퍼즐과 함께 해주실 예정입니다.