매월 정답자 한 분을 선정하여 고등과학원에서 소정의 상품을 드릴 예정입니다.
퍼즐 참여는 2월 27일까지 가능하며 다음달 초 해설과 함께 정답자가 공개됩니다.
(답안과 함께 이름, 연락처를 남겨주셔야 정답자 선정 연락이 가능합니다!)
다면체의 전개도란, 쉽게 말하자면 접어서 그 다면체를 만들 수 있는 종잇조각을 말한다. 즉, 전개도로써 성립하기 위해서는 종이를 적당히 잘라서 그 전개도를 만들 수 있어야 한다.
우리가 흔히 보는 볼록다면체들은 모두 한 꼭짓점에 모이는 면들의 각의 합이 360도 미만인 다면체들이다. 예를 들어 아래 그림들을 보자. 정사면체는 한 꼭짓점에서 정삼각형 3개가 만나서 각의 합이 180도가 되고, 정팔면체는 4개가 만나서 240도가, 정이십면체는 5개가 만나서 300도가 된다.
이렇게 한 꼭짓점에 모이는 면들의 각의 합이 360도 미만이기 때문에 전개도를 접어서 입체로 만들 수 있는 것이다. (엄밀한 정의는 아니지만, 이러한 입체도형들은 각 꼭짓점에서의 곡률이 양수라고 말할 수 있겠다.) 아래의 그림을 보면, 정삼각형 6개가 한 꼭짓점에서 만나도록 하면 합이 정확히 360도가 되어 그 꼭짓점 주변은 평면이 되어 버리니까 입체도형이 아니게 된다는 것을 알 수 있다. (이 경우에는 이 꼭짓점에서의 곡률이 0이라고 말할 수 있겠다.)
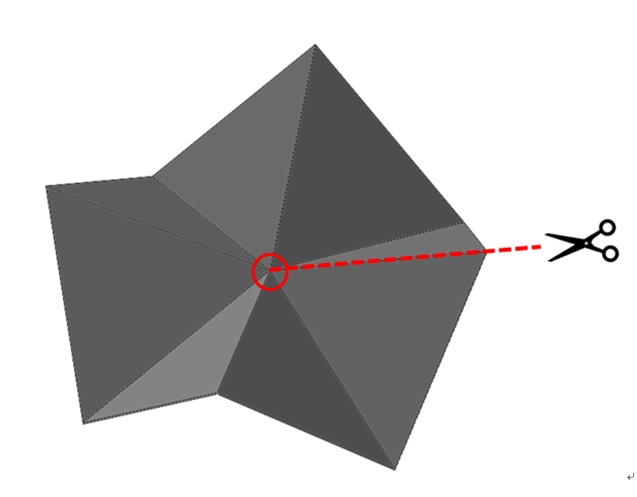
하지만, 오히려 360도를 초과하면 그 꼭짓점 주변은 입체가 될 수 있다. 예를 들어, 정삼각형 8개가 한 꼭짓점에서 만나는 경우를 그린 아래 그림을 보자. (이 경우에는 이 꼭짓점에서의 곡률이 음수라고 말할 수 있겠다.) 이 꼭짓점 주변에서 모이는 각의 합은 480도로, 360도를 초과했기 때문에 입체가 되었다.
하지만 위 그림에서 점선으로 표시한 것처럼 이 꼭짓점 주변의 모서리 하나를 잘라 펼쳐서 전개도를 만들려고 시도하면, 이 꼭짓점 주변에서 모이는 면들의 각의 합이 360도가 넘기 때문에 전개도가 자기 자신과 겹치게 된다. 전개도가 자기 자신과 겹친다는 말은 다시 말해 한 장의 종이를 잘라서 만들 수 있는 전개도가 아니라는 뜻이다. 이렇게 전개도가 자기 자신과 겹치는 경우는 주변에 모이는 면들의 각의 합이 360도를 넘는 모든 꼭짓점에서 발생할 수 있다.
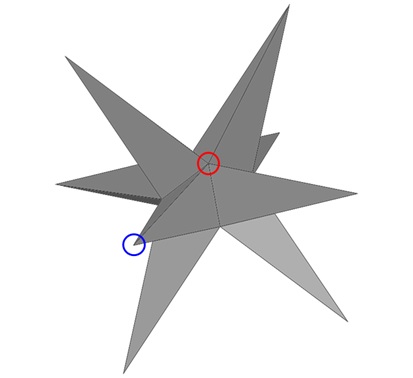
충명은 한 장의 종이를 가지고 다음과 같은 입체도형을 만들고 싶어 한다.
이 다면체는 정팔면체의 각 면에 삼각뿔을 붙여 만든 것으로, 겉면에 보이는 이등변삼각형들은 모두 합동이고 30도, 75도, 75도의 내각을 갖는다. 이 다면체의 바깥쪽 꼭짓점에 모이는 각의 합은 30도씩 3면으로 총 90도이지만 (파란색 원으로 표시), 안쪽 꼭짓점에서는 75도씩 8면으로 총 600도인 것을 관찰할 수 있다 (빨간색 원으로 표시). 정팔면체의 각 면에 정사면체를 붙여 얻은 입체도형의 이름이 별팔면체Stellated Octahedron이므로, 충명은 위 그림의 다면체를 뾰족한 별팔면체 라고 이름 붙이기로 했다.
어떻게 하면 종이 한 장을 잘라 만들 수 있는, 즉 자기 자신과 겹치지 않는 뾰족한 별팔면체의 전개도를 그릴 수 있을까? 그런 전개도를 그려 보자. 실제로 접어서 뾰족한 별팔면체가 만들어지는지 확인해 보면 더욱 좋을 것이다. 물론, 전개도는 다면체의 모서리를 따라서만 접거나 자를 수 있다. 면의 내부를 침범해서는 안 된다.
그러한 전개도를 찾는 데 성공한 사람을 위한 도전과제가 있다. 찾아낸 전개도는 정팔면체에 붙인 삼각뿔이 더 뾰족할 때도 성립하는가? 가령, 이등변삼각형의 내각이 10도, 85도, 85도일 경우에도 찾아낸 전개도가 자신과 겹치지 않느냐는 것이다. 그렇지 않다면, 붙인 삼각뿔이 아무리 뾰족하더라도 자신과 겹치지 않는 더 뾰족한 별팔면체의 전개도를 찾아보자.