리오빌 양자중력: 무작위 곡면의 성질에 관하여

우리 세상에는 무작위로 움직이는 것처럼 보이는 대상들이 많이 있습니다. 공기 중을 날아다니는 새와 미시적으로 움직이는 주식 가격 등 일상 생활에서 쉽게 접하는 많은 대상들이 무작위성의 성질을 가지고 있습니다. 이러한 실생활의 수많은 예시들은 시간이라는 1차원 매개변수^parameter 에 따라 무작위하게 변하는 곡선^curve 이라고 불리는 대상입니다.

                                           리오빌 양자중력 곡면 Jérémie Bettinelli

그렇다면 매개변수가 하나 더 주어질 때, 즉 두 개의 매개변수에 의해서 무작위로 변하는 대상은 무엇이 있을까요? 두 개의 매개변수를 가지는 대상을 곡면^surface라고 부릅니다. 예를 들어서, 돔 구장에서의 볼록하게 튀어나온 돔이나 공기 중을 떠다니는 비눗방울 모두 곡면이라고 볼 수 있습니다. 그렇다면 무작위하게 움직이는 곡면을 어떻게 묘사할 수 있을까요? 이번 호에서는 수학 뿐 아니라 물리학의 통계역학, 초끈이론 등 다양한 분야와 밀접한 연관성이 있는 리오빌 양자중력 곡면^{Liouville quantum gravity surface} 에 대해서 간략히 소개하고자 합니다.

무작위 걸음과 위너 과정

무작위 곡면을 설명하기 전에, 기본적인 무작위 모델인 무작위 걸음^{random walk} 을 이야기해보고자 합니다.격자판 위에서 무작위하게 움직이는 물체의 움직임을 생각해 봅시다. 즉, 현재 지점에서 인접한 지점들 중 한 지점으로 균등한 확률로 움직인다고 가정해 봅시다. 예를 들어서, 1차원 직선 상에서는 오른쪽 지점으로 1/2 확률, 왼쪽 지점으로 1/2 확률로 움직입니다.

이러한 무작위 걸음의 거시적인 움직임은 비교적 간단하게 묘사될 수 있습니다.시간이 무한대로 갈 때, 무작위 걸음의 (거시적인) 자취는 가우시안 분포^{Gaussian distribution} 를 가지는 무작위 곡선으로 수렴한다는 사실이 알려져 있습니다. 이는 수학적인 용어로 위너 과정^{Wiener process} 이라고 불리는데, 액체나 기체 속에서 불규칙하게 운동하는 입자들의 움직임을 묘사하는 브라운 운동^{Brownian motion} 을 수학적으로 나타낸 것입니다. 여기서 가우시안 분포는 어떤 모집단의 분포를 나타낼때 대표적으로 쓰이는 분포로, 다음과 같은 분포형태를 가집니다.

여기에서 흥미로운 점은 보편성^universality 이라 불리는 원리입니다. 즉, 앞서 언급한 특정한 형태의 무작위 걸음 외에도 다양한 다른 형태의 무작위 걸음에 대해서도 거시적인 움직임은 항상 가우시안 성질을 가집니다. 예를 들어, 반드시 인접한 지점이 아니더라도 먼 지점으로 점프하는 형태의 무작위 걸음에 대해서도 이의 거시적인 움직임은 가우시안 분포를 갖는 위너 과정으로 나타나게 됩니다.

무작위 평면 그래프

위너 과정은 시간이라는 1차원 매개변수를 가지는 무작위 곡선으로, 앞서 언급한 보편성 원리로 인해 시간의 흐름에 따라 무작위한 움직임을 하는 대상을 모델링하는데에 대표적으로 사용됩니다. 그렇다면, 자연스럽게 다음과 같은 질문을 던질 수 있습니다.

질문: 1차원이 아닌 2차원 매개변수를 갖는 보편성 원리를 포함하고 있는 무작위 대상이 무엇인가?

1차원 매개변수를 갖는 대상이 위너 과정같은 곡선^curve 이라면, 2차원 매개변수를 갖는 대상은 곡면^surface 입니다. 무작위 곡선의 이산^discrete 버전이 앞서 언급한 무작위 걸음이라고 할 수 있다면, 곡면의 이산 버전은 평면그래프^{planar graph} 라고 볼 수 있습니다.

평면 그래프를 이야기하기 전에 이산수학^{Discrete Mathematics} 에서 자주 등장하는 그래프^graph 에 관하여 간략히 이야기해보겠습니다. 그래프란 점들과 그 사이를 연결하는 선들로 구성된 대상입니다. 예를 들어서, 사람들의 모임을 생각할 때, 각 사람을 점으로 간주하고 두 사람이 서로 알 때 이 두 점을 선으로 연결했을 때 그래프를 하나 얻어낼 수 있습니다. 이렇게 선들이 그래프 상에 주어질 때, 두 점 사이의 거리를 구할 수 있습니다. 즉, 거리는 한 점에서 다른 점으로 이동하기 위해 거쳐야 하는 선의 최소 개수로 자연스럽게 정의할 수 있습니다.

예를 들어서, 위 그래프에서 두 점 0과 1 사이의 거리는 1이지만, 0과 3 사이의 거리는 2입니다. 이를 통해, 그래프를 이산 거리 공간^{discrete metric space}로 간주할 수 있습니다.

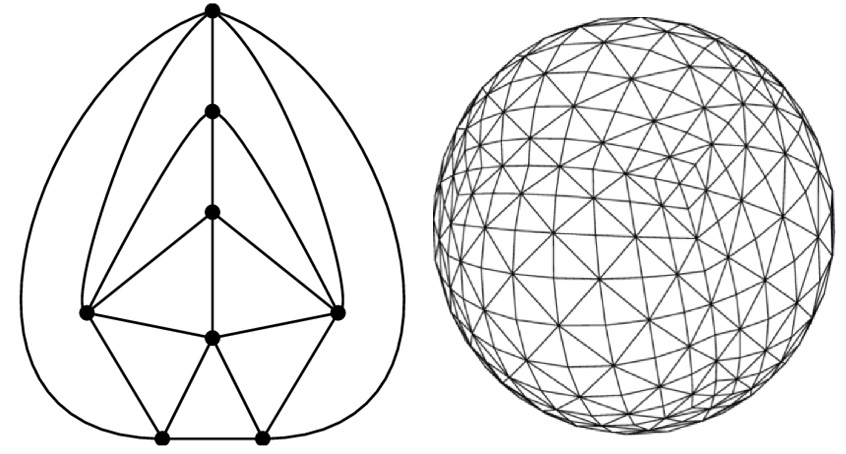
이제부터 그래프들 중에서 평면그래프라고 불리는 특수한 그래프를 고려할 것입니다. 평면그래프란, 선들이 서로 교차하지 않는 그래프입니다.평면그래프가 주어질 때에 선들로 구성된 면들을 생각할 수 있고, 매우 특수한 상황으로, 각 면들이 모두 삼각형으로 주어진 다음 왼쪽 그림과 같은 평면그래프를 생각해볼 수 있습니다.

 

  ^그림3(좌) 삼각화 평면그래프 / Ervin Gyori, Addisu Paulos, Oscar Zamora 

  ^그림4(우) 2차원 구 상에서의 삼각화 / Gustavo Montero

이제 2차원 구^sphere 를 하나 생각하고, 이를 위의 오른쪽 그림처럼 무작위로 삼각화를 시킵니다. 삼각화를 시키는 방법은 무한히 많지만, 어느 한 삼각화를 2차원 구를 잘 조정하여 (위상동형^{homeomorphism}) 다른 삼각화로부터 얻어낼 수 있다면 이 두 삼각화를 같다고 가정해봅시다. 이 삼각화 평면그래프를 앞서 언급했듯이 이산 거리 공간으로 생각할 수 있습니다. 물론 이 그래프의 점의 개수가 무한대로 늘어날수록 두 점 사이의 거리도 일반적으로 무한대로 늘어날 것이고 거리공간이 매우 복잡해질 것입니다. 놀랍게도, 이 평면그래프의 거시적인 성질에 대한 정확한 묘사가 가능합니다. Jean-Francois Le Gall 교수님은 다음 정리를 증명하였습니다.[8]

정리. 삼각화 평면그래프의 점의 개수가 무한대로 커질 때, 이 거리공간은 특정한 무작위 거리공간으로 수렴한다. 보다 더 자세히 말하자면, 삼각화 평면그래프의 점의 개수를 \(n\)이라 한다면, 이 \(n\)개 점 사이의 거리들을 \(n^{1/4}\) 로 나눈 후 적절한 상수를 곱하면 (\(n\)이 무한대로 커질 때) 어떠한 특정 무작위 거리공간으로 수렴한다.

여기에서 거리공간이 어떠한 거리공간으로 수렴한다^{Gromov–Hausdorff convergence} 는 말은, 두 거리공간이 갖는 기하학적인 성질이 거의 같아진다는 뜻입니다. 이 정리에서 매우 흥미로운 점은, 각 면이 삼각형이 아니더라도 사각형, 오각형 등의 (점의 개수가 \(n\)개인) 평면그래프들에 대해서도 점들 사이의 거리를 \(n^{1/4}\) 로 나눈 후 적당한 상수를 곱하면 전부 똑같은 거리공간으로 수렴한다는 것입니다. 각 면이 가지는 변의 개수가 달라지면 이 평면그래프들의 거리공간은 상당히 달라지게 됩니다. 그러나 놀라운 점은, 평면그래프의 크기가 무한대로 커지면 이 서로 다른 거리공간들의 거시적인 행동은 일정하게 나타난다는 것입니다. 이 사실은 Grégory Miermont 교수님에 의해 증명되었습니다.[9] 이것은 앞서 언급한 어떠한 종류의 무작위 걸음도 결국에는 위너 과정이라는 일정한 대상으로 수렴한다는 사실의 2차원 버전의 보편성 원리라고 간주할 수 있습니다. 이 2차원 무작위 거리공간은 브라운 맵^{Brownian map} 이라고 불립니다.

하우스도르프 차원^{Hausdorff dimension}

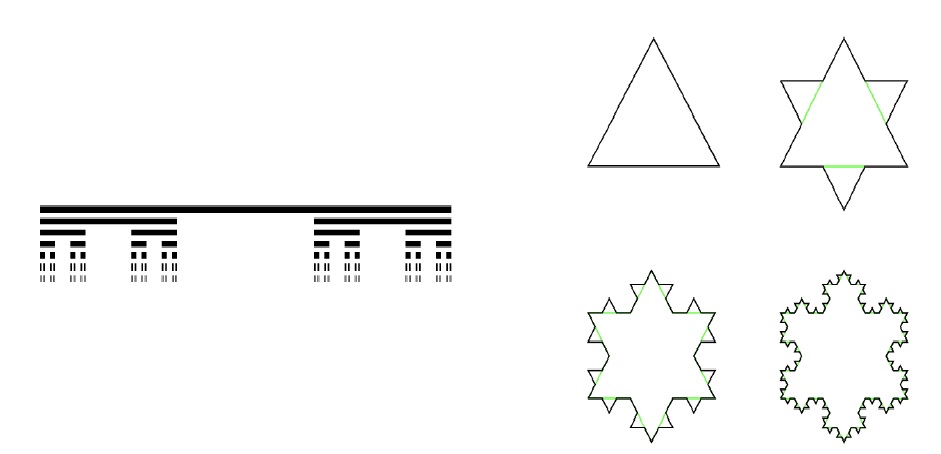
수학의 여러 분야에서 자연스럽게 등장하는 프랙털^fractal 이라는 개념은 대상의 자기닮음 성질이나 거친 정도를 의미합니다.하우스도르프 차원은 대상이 얼마나 프랙털한 성질을 가지는지 정량화시키는 척도입니다. 프랙털한 성질을 가지는 대표적인 예시로 아래 왼쪽 그림의 칸토어 집합^{Cantor set} 이 있습니다. 칸토어 집합은 구간 \([0,1]\)부터 시작하여 각 구간을 3등분하여 가운데 구간을 반복적으로 제외하는 방식으로 만들어진 대상입니다. 이는 자기닮음 성질을 가지는데, 칸토어 집합을 \(1/3\) 크기로 줄이면 원래 칸토어 집합의 왼쪽과 오른쪽 부분과 같게 됩니다. 각 단계마다 구간 3개 중 1개가 제외되고 2개만 유지되기 때문에, 칸토어 집합은 \(\frac{\log 2}{\log 3}\) 이라는 하우스도르프 차원을 가집니다. 빈 공간이 많고 원소들이 매우 드물게 나타나기 때문에, 칸토어 집합은 1보다 작은 하우스도르프 차원을 가집니다.

비슷한 예시로 아래 오른쪽 그림의 자기닮음 성질을 가지는 눈꽃 모양을 생각할 수 있습니다. 각 선분을 3등분하여 가운데 구간을 지우는 대신에 산 모양의 선 2개를 첨가합니다. 각 단계마다 선분의 개수가 3개에서 4개로 증가하기 때문에, 하우스도르프 차원은 \(\frac{\log 4}{\log 3}\) 로 나타나게 됩니다. 1차원인 선으로만 이루어진 대상이지만 이러한 프랙털한 성질 때문에 하우스도르프 차원이 1보다 크게 됩니다.

이제 본론으로 들어가서, 처음에 언급한 무작위 걸음의 거시적인 움직임을 묘사하는 위너 과정의 하우스도르프 차원에 관해 간략하게 이야기하고자 합니다. 무작위로 움직이는 위너 과정은 매우 거친 움직임을 가집니다. 예를 들어서, 위너 과정의 움직임은 연속적이지만, 미분 가능하지 않습니다. 1차원 직선에서 움직이는 위너 과정의 그래프는 하우스도르프 차원이 3/2로, 1보다 크다는 사실이 알려져 있습니다. 즉, 위너 과정은 위의 눈꽃 프랙털 모양처럼 꼬불꼬불하고 거친 자취를 가진다는 사실을 알 수 있습니다.

그 다음으로, 무작위 평면그래프의 극한으로 나타나는 브라운 맵의 하우스도르프 차원에 대한 질문을 비슷하게 할 수 있습니다. 위너 과정과 마찬가지로, 이 브라운 맵 또한 매끄럽지 않고 거친 성질을 가집니다. 브라운 맵의 하우스도르프 차원은 정확하게 알려져 있는데, Jean-Francois Le Gall 교수님은 브라운 맵의 하우스도르프 차원은 4가 된다는 사실을 증명했습니다.[7]

브라운 맵의 하우스도르프 차원 4는 곡면의 매개변수 2차원보다 크기 때문에, 브라운 맵은 거칠고 프랙털한 성질을 가진다는 것을 알 수 있습니다. 이 4라는 숫자는, 삼각화 평면그래프에서의 공의 부피가 반지름의 4제곱으로 증가한다는 것과 관련이 있습니다. 즉, 삼각화 평면그래프의 한 점을 중심으로 거리가 \(n\) 이하가 되는 점들의 개수가 대략적으로 \(n^4\)의 속도로 증가한다는 것입니다.

리오빌 양자중력

이제 본론으로 들어가서, 리오빌 양자중력^{Liouville Quantum Gravity} 에 관하여 이야기해보고자 합니다.리오빌 양자중력은 매우 거칠고 프랙털한 성질을 가지는 무작위 곡면 random surface 으로, 무작위하게 움직이는 곡면을 표현하는 자연스러운 모델입니다. 이 리오빌 양자중력은 물리학의 통계역학^{statistical mechanics}, 초끈이론^{string theory}, 등각장 이론^{conformal field theory} 등에서 영감을 받아 프랙털한 성질을 가지는 자연스러운 곡면을 어떻게 모델링하는지 질문에서 시작되었습니다.

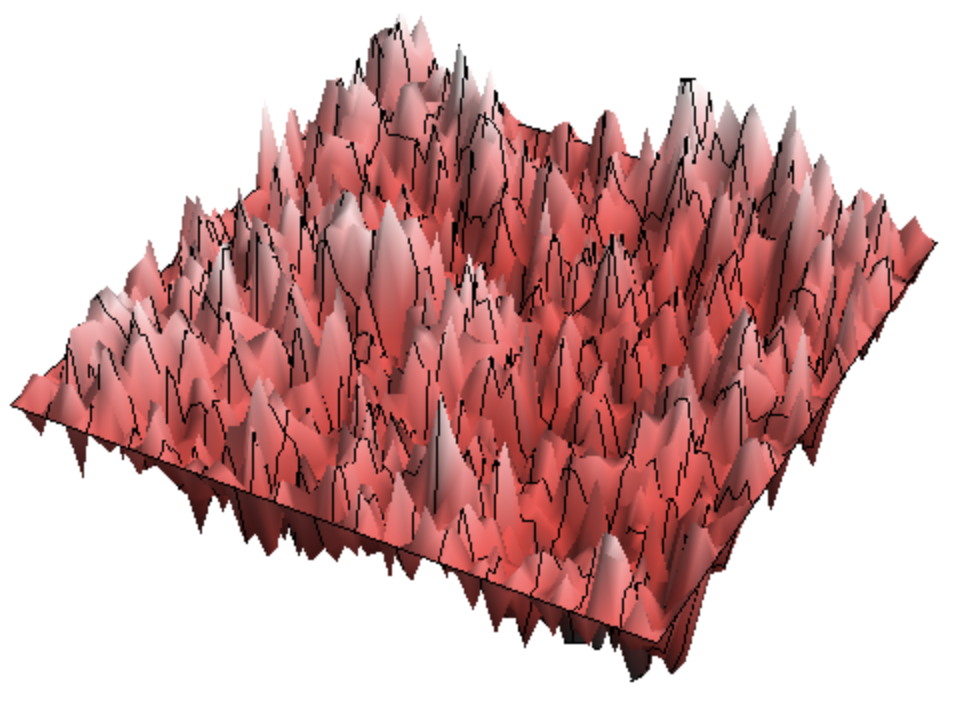
리오빌 양자중력은 가우시안 자유장^{Gaussian Free Field} 이라는 특수한 종류의 랜덤 곡면을 지수화^exponentiate 한 대상입니다.가우시안 자유장이란, 통계역학의 매우 기본적인 가우시안 모델들 중 하나로, 다양한 입자시스템의 거시적인 움직임을 묘사하는 데에 등장합니다. 다음 그림은 가우시안 자유장의 한 샘플을 예시로 보여줍니다.

\(h\)를 가우시안 자유장의 높이라고 가정해 봅시다. 리오빌 양자중력은, 높이 \(h\)를 \(\gamma\) 라는 매개변수를 이용하여 지수화시켜 얻어지는 대상입니다.

\begin{align*}
e^{\gamma h}
\end{align*}

높이 \(h\)는 함수로 정의가 되지 않기 때문에, 이를 지수화하기 위해서는 엄밀한 수학적인 과정을 거쳐야 합니다. 이 과정은 실제로 매우 까다로우며, 복잡한 확률론적 아이디어를 필요로 합니다.이 리오빌 양자중력은 \(\gamma\)의 값에 따라 성질이 크게 변하게 됩니다. 예를 들어서, 가장 간단한 경우인 \(\gamma=0\) 일 때는 평범한 2차원 평면을 얻어내지만, \(\gamma\)의 값이 커질수록 이 곡면은 프랙털한 성질을 가지게 됩니다.

리오빌 양자중력은 측도적인^{measure theoretical} 측면에서 Bertrand Duplantier‬ 교수님과 Scott Sheffield 교수님‪에 의해 중요한 연구가 진행되었습니다.[3] 리오빌 양자중력은 \(\gamma\)의 값이 2가 되는 기점으로 성질이 크게 바뀌게 됩니다. \(\gamma\) 의 값이 2 이상이면 리오빌 중력장은 자명한 경우가 되며 (\(e^{\gamma h}=0\)), \(\gamma\)의 값이 0과 2 사이가 되면 프랙털한 성질을 가집니다. 보다 더 자세히 말하자면, 리오빌 양자중력은 하우스도르프 차원이 \(2-\gamma^2/2\) 인 집합 위에서 정의가 됩니다. 즉, \(\gamma\)의 값이 0에 가까워지면 비교적 넓은 공간 위에서 정의되고, 극단적으로 \(\gamma\)의 값이 2에 가까워질수록 매우 좁은 집합 위에서 정의되는 프랙털한 무작위 곡면이 됩니다.

반면에, 리오빌 양자중력을 기하학적인 측면에서 이해하는 것은 훨씬 더 어려운 문제입니다. 두 점 사이의 거리를 이해하기 위해서는 두 점을 연결하는 모든 곡선에 대한 길이를 구한 다음, 이들의 최소값을 구해야 합니다. 그러나 리오빌 양자중력의 경우 곡선의 길이가 복잡한 확률변수로 주어지기 때문에, 이들을 종합적으로 이해하는 것은 매우 까다로운 작업을 요구로 합니다. 그렇지만 매우 최근에, 두 그룹 Jian Ding-Julien Dubedat-Alexander Dunlap-Hugo Falconet[1] 와 Ewain Gwynne-Jason P. Miller[6] 에 의해서 큰 진전이 있었습니다. 이 두 그룹은 리오빌 양자중력 곡면에 자연스러운 거리공간을 부여할 수 있음을 증명하였습니다.

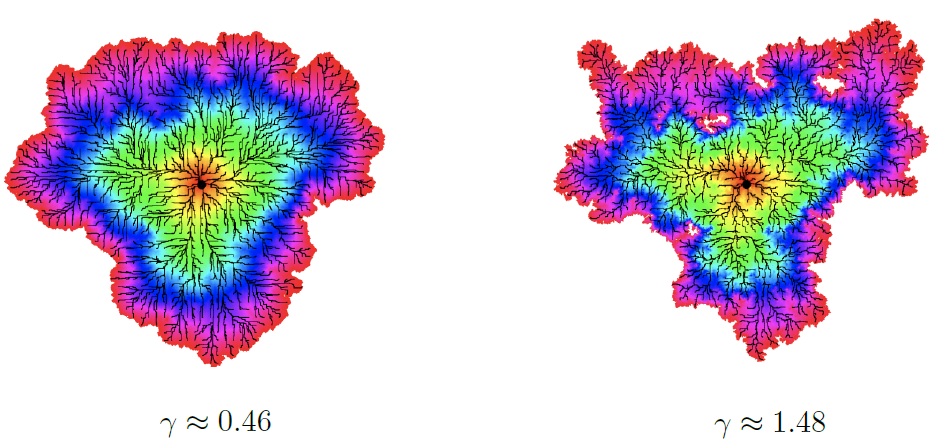
아래 두 그림은 리오빌 양자중력의 서로 다른 \(\gamma\)의 값에 따라 원의 모양이 어떻게 변화하는지 묘사합니다. 가운데 검은색 점을 중심으로, 동색의 점들은 검은색 중심점과 같은 거리에 떨어져 있습니다. \(\gamma\)의 값이 더 클수록, 이 원들의 모양이 더 꼬여있고 프랙털하다는 사실을 알 수 있습니다.

측지선^geodesic 의 성질

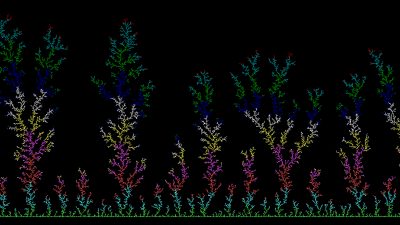
리오빌 양자중력 곡면에서의 거리공간은 일반적인 실생활에서 경험하는 거리공간과 큰 차이점을 가집니다. 두 점 사이를 연결하는 가장 짧은 경로를 측지선^geodesic 이라고 합니다. 우리가 살아가는 공간에서 본인의 위치가 고정되어 있다고 가정해 봅시다. 이 때, 본인과 다른 사람들의 위치를 연결하는 측지선은 항상 직선으로 나타나고, 측지선의 방향은 0도부터 360도까지 다양하게 나타날 수 있습니다. 그렇지만, 리오빌 양자중력에서는 이와 완전히 다른 측지선의 성질이 나타나게 됩니다. 본인과 다른 사람들의 위치를 연결하는 측지선들은 모두 특정한 지점에서 교차해야 합니다. 즉, 측지선들을 모아놓으면 나뭇가지 Tree 들이 뻗어나오는 형태로 나오게 됩니다. 위 그림에서 검은색 선들은 가운데 검은색 점을 중심으로 뻗어나가는 측지선들을 표현합니다. 이 측지선들이 나뭇가지 형태로 갈래를 펼쳐나간다는 사실을 알 수 있습니다. 이러한 흥미로운 결과는 Ewain Gwynne 교수님과 Jason P. Miller 교수님에 의해 도출되었습니다.[5]

위의 그림에서 볼 수 있듯이, 측지선을 표현하는 검은색 선들은 일반적인 직선과는 달리 꼬불꼬불하게 구성되어 있음을 알 수 있습니다. 이를 통해, 리오빌 양자중력 곡면에서의 측지선들은 하우스도르프 차원이 1보다 크게 될 것이라는 추측을 할 수 있습니다. 그렇지만 앞서 언급하였듯이 측지선의 프랙털 성질을 이해하기 위해서는 두 점 사이를 연결하는 모든 곡선들의 거리에 대한 정보를 알아야 하기 때문에, 이는 매우 까다로운 문제입니다. 최근에 두 그룹 Jian Ding-Subhajit Goswami[2] 와 Jian Ding-Fuxi Zhang[4] 은 리오빌 양자중력의 이산 버전에서 \(\gamma\)가 충분히 0에 가까운 값을 가질 때 측지선의 하우스도르프 차원이 1보다 크다는 사실을 증명했습니다.

브라운 맵

앞서 브라운 맵은 삼각화와 사각화 등 다양한 무작위 평면 그래프의 거시적인 기하학적인 성질을 묘사하는 무작위 거리 공간이라는 사실을 언급하였습니다.놀랍게도,
Jason P. Miller 교수님과 Scott Sheffield 교수님은 브라운 맵은 리오빌 양자중력의 \(\gamma=\sqrt{8/3}\) 인 특수한 경우라는 사실을 증명하였습니다.[10] 즉, 리오빌 양자중력 곡면은 브라운 맵을 포함하는 매우 일반적이고 자연스러운 형태의 무작위 곡면이라는 사실을 알 수 있습니다.

마지막으로, 리오빌 양자중력 이론에서 현재 활발히 연구되고 있는 흥미로운 문제들에 대해 언급하겠습니다.

질문: 리오빌 양자중력 곡면의 하우스도르프 차원은 얼마인가?

이 질문에 대한 답은 \(\gamma=\sqrt{8/3}\) 인 경우에만 알려져 있으며, 이 경우에는 하우스도르프 차원이 4가 됩니다. 리오빌 양자중력이 얼마나 프랙털한지 알아내는 문제는 매우 흥미로운 문제입니다.

질문: 일반적인 리오빌 양자중력 곡면을 무작위 평면그래프의 극한으로 표현할 수 있는가?

초반부에서 언급한 브라운 맵, 즉 \(\gamma=\sqrt{8/3}\) 인 경우에는 균등하게 선택한 무작위 삼각화 평면그래프의 극한으로 나타납니다. 다른 \(\gamma\)의 값에 대해서 어떠한 무작위 평면그래프의 극한으로 나타나는지 알아내는 것 또한 중요한 문제입니다.