3월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
3월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 조한슬님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
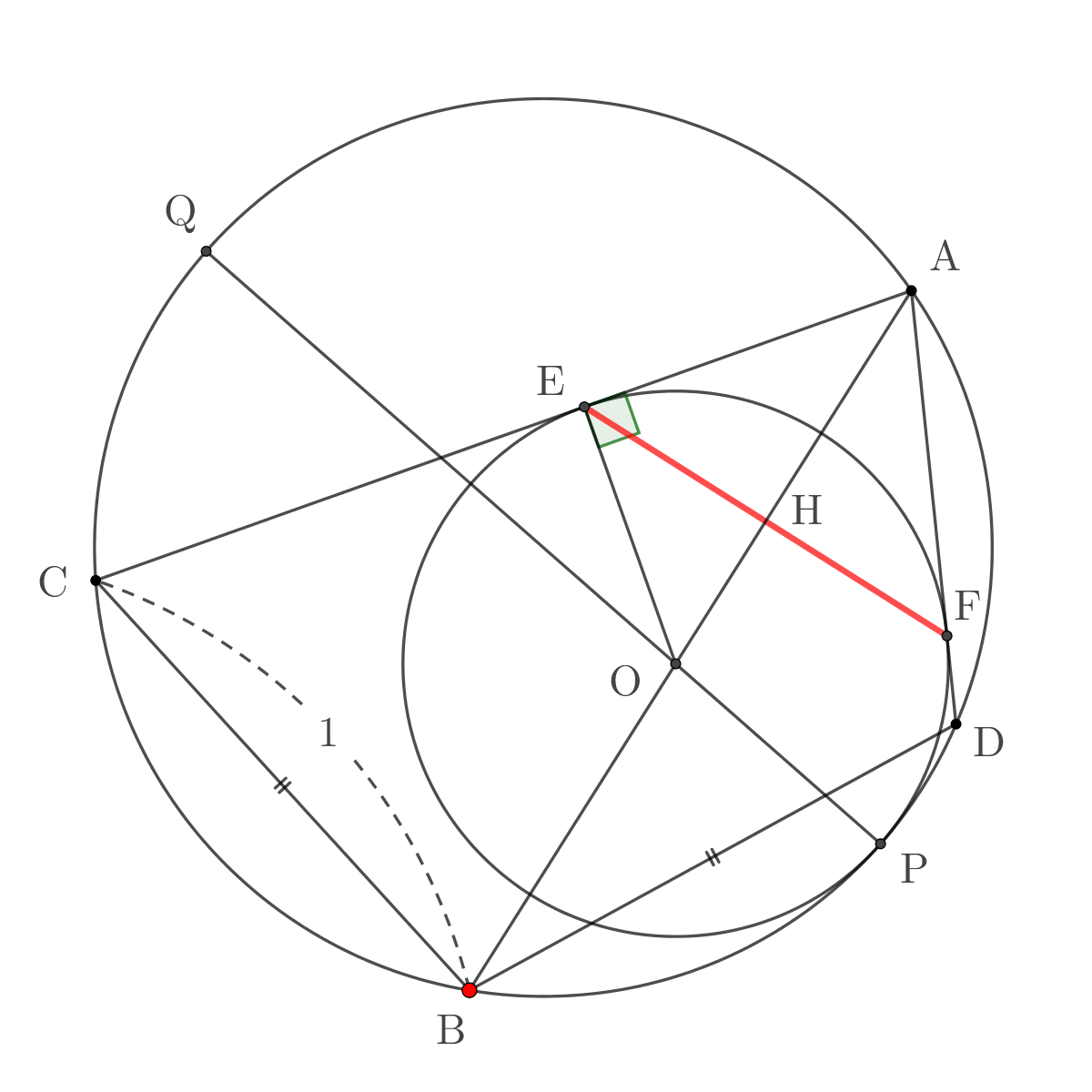
\(\overline{\mathrm{BC}} = \overline{\mathrm{BD}}\)에서 호 \(\mathrm{BC}\)와 호 \(\mathrm{BD}\)가 같은 길이임을 알고, 따라서 \(\angle \mathrm{BAC} = \angle \mathrm{BAD}\)임 또한 알 수 있다. 작은 원의 중심을 \(\mathrm{O}\)라 하면, \(\triangle \mathrm{OEA} \equiv \triangle \mathrm{OFA}\) (RHS)로 \(\angle \mathrm{OAE} = \angle \mathrm{OAF}\)임을 안다. 여기서 우리는 \(\mathrm{O}\)가 선분 \(\mathrm{AB}\) 위에 있음을 알 수 있다.
선분 \(\mathrm{EF}\)와 선분 \(\mathrm{AB}\)의 교점을 \(\mathrm{H}\)라 하면, \(\overline{\mathrm{AE}} = \overline{\mathrm{AF}}\)이고 \(\overline{\mathrm{AH}}\)가 공통으로 \(\triangle \mathrm{EHA} \equiv \triangle \mathrm{FHA}\) (SAS) 이다. 따라서 \(\angle \mathrm{EHA} = \angle \mathrm{FHA} = 90^\circ\)가 되고, \(\overline{\mathrm{EF}} \perp \overline{\mathrm{AB}}\)가 되어 우리가 구하고자 하는 거리는 \(\overline{\mathrm{BH}}\)가 된다.
큰 원의 반지름을 \(R\), 작은 원의 반지름을 \(r\), \(\angle \mathrm{BAC} = \alpha\), \(\overline{\mathrm{BH}} = d\)라 하자. 두 직각삼각형 \(\mathrm{OEA}\)와 \(\mathrm{OHE}\)에서,
\begin{align*}
\sin\alpha &= \frac{r}{\overline{\mathrm{OA}}}, \\
\sin\angle \mathrm{OEH} = \sin\alpha &= \frac{\overline{\mathrm{OH}}}{r}
\end{align*}
를 얻는다. 두 원의 접점을 \(\mathrm{P}\), 직선 \(\mathrm{OP}\)가 원과 만나는 또다른 점을 \(\mathrm{Q}\)라 하자. 이때 선분 \(\mathrm{OP}\)가 두 원의 동통접선에 수직이므로 선분 \(\mathrm{PQ}\)는 큰 원의 지름이 된다. 따라서, \(\overline{\mathrm{OP}}\cdot\overline{\mathrm{OQ}} = \overline{\mathrm{OA}}\cdot\overline{\mathrm{OB}}\)를
\begin{align*}
\overline{\mathrm{OP}}\cdot(\overline{\mathrm{PQ}}-\overline{\mathrm{PO}}) &= \overline{\mathrm{OA}}\cdot(\overline{\mathrm{BH}}-\overline{\mathrm{OH}}) \\
r(2R-r) &= \frac{r}{\sin\alpha}(d-r\sin\alpha)
\end{align*}
로 다시 쓸 수 있다. 정리하면 \(d = 2R\sin\alpha\)를 얻는데, 삼각형 \(\mathrm{ABC}\)에 대하여 사인법칙을 적용하면 \(2R = \frac{1}{\sin\alpha}\)이다. 그러므로 구하고자 하는 거리는 \(d = 1\)이 된다.
다음은 3월의 정답자로 선정된 조한슬님의 해설입니다.
첨부 이미지처럼 점들을 표시해 보겠습니다. 문제의 조건대로, AB =AD=1입니다. 이 두 선분은 큰 원의 현인데 그 길이가 같으므로 그에 대한 원주각도 같습니다. (각ACB=각ACD) 이때의 원주각의 크기를 세타(θ)라고 놓겠습니다. 한편 작은 원은 선분 BC, CD에 접하므로 이 작은 원의 중심(O’)은 각BCD의 이등분선, 즉 선분 AC 위에 놓입니다. 게다가 삼각형 CEF는 이등변삼각형이 되므로, 선분 AC와 EF는 점 H에서 직교합니다. 따라서 우리가 알아야 할 빨간 점(A)에서 빨간 선분(EF)까지의 거리는 AH의 길이와 같습니다. 큰 원과 작은 원의 반지름을 각각 R, r이라 놓겠습니다. 그럼 일단 사인법칙에 의해 sin θ = 1/2R을 만족합니다. 삼각함수의 정의를 활용하면 O’H= r sin θ=r/2R, O’C= r/ sin θ = 2Rr 등을 알 수 있습니다. 이제 O’A의 길이만 알면 됩니다. 한 점에서 만나는 두 현의 성질에 의해, (O’A)*(O’C)=(O’G)*(O’I) 입니다. 이때 GI는 큰 원의 지름입니다. O’I=r, O’G=2R-r이므로, (O’A)*2Rr=2Rr-r^2 이고, 즉 O’A=1-(r/2R)이 됩니다. 따라서 구하려는 길이는 AH = O’A+O’H =1-(r/2R)+(r/2R)=1입니다!