[4월의 퍼즐] 라틴 방진을 품은 라틴 방진

라틴 방진은 N×N 크기 정사각형 격자의 각 칸에 서로 다른 N가지 기호를 채워 넣어서, 각 행과 열에 N가지 기호가 모두 한 번씩 등장하게 만든 배열이다. 편의를 위해 N가지 기호 대신 1부터 N까지의 수 배열이라고 생각하자.

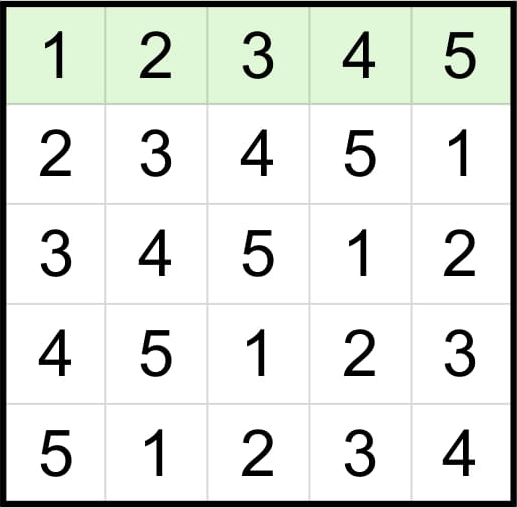
라틴 방진을 만드는 방법은 여러 가지가 있는데, 가장 간단하게 생각할 수 있는 방법은 다음과 같다. 먼저 첫 번째 행에 1부터 N까지의 수를 순서대로 적는다. 두 번째 행에는 첫 번째 행을 왼쪽으로 한 칸 회전한 배열을 적는다. 왼쪽으로 한 칸 회전한다는 것은 가장 왼쪽의 수를 가장 오른쪽으로 옮기는 것을 의미하며, 첫 번째 행을 왼쪽으로 한 칸 회전하고 나면 2, 3, ⋯, N, 1이 된다. 세 번째 행에는 두 번째 행을 왼쪽으로 한 칸 회전한 배열, 즉 3, ⋯, N, 1, 2를 적는다. 이를 반복해서 N개의 행을 모두 채우면 다음 그림과 같은 라틴 방진이 만들어진다.

이번 달의 퍼즐에서는 배열 안에 또 다른 라틴 방진을 품은 라틴 방진을 만들어 보자. 어떤 N과 M에 대해서, N×N 라틴 방진 안에 더 작은 라틴 방진을 이루는 M×M 배열이 존재하도록 라틴 방진을 만드는 것이 이번 퍼즐의 목표이다.

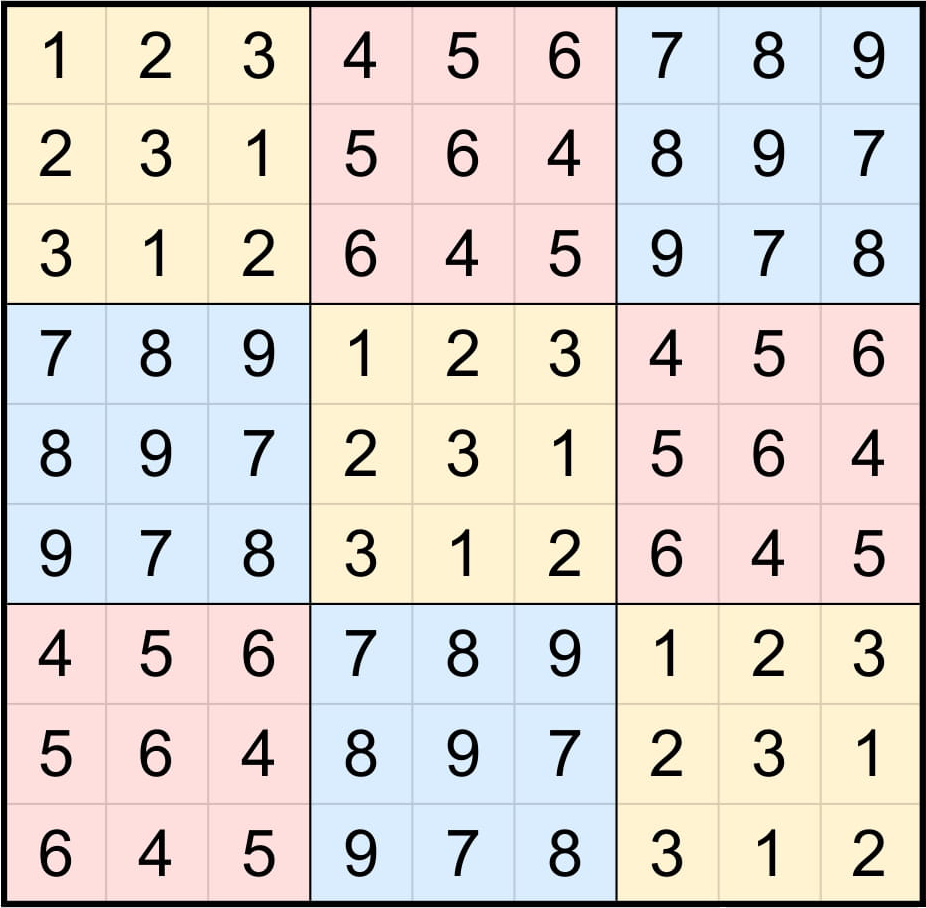
가장 간단하게 생각할 수 있는 예시는 M이 N의 약수인 경우이다. \(N = MK\) 일 때, K×K 라틴 방진의 각 칸에 서로 다른 기호 대신 서로 다른 M×M 라틴 방진을 채워 넣는 아이디어를 이용하는 것이다. 그러면 총 \(K^2\)개의 M×M 라틴 방진을 품은 N×N 라틴 방진이 된다.

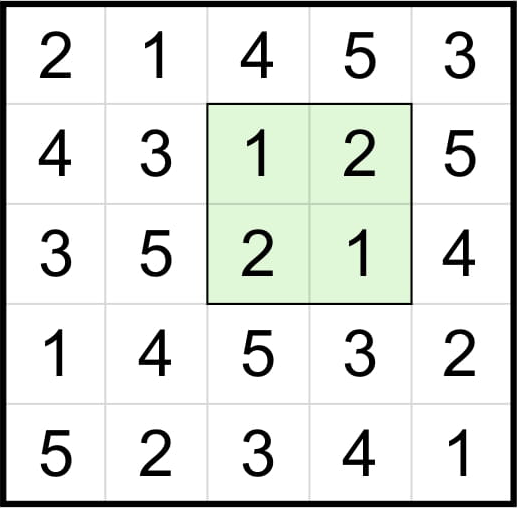
물론 M이 N의 약수가 아닌 경우에도 라틴 방진을 품은 라틴 방진을 만들 수 있다. 다음 예시는 2×2 라틴 방진을 품은 5×5 라틴 방진이다.

그렇다면 일반적으로 M×M 라틴 방진을 품은 N×N 라틴 방진을 만들 수 있는 N, M의 조건은 무엇일까? 다음 문제들을 풀어 보며 고민해 보자.

1. 5×5 라틴 방진을 품은 8×8 라틴 방진을 만들 수 있을까? 가능하다면 만들어 보고, 불가능하다면 증명해 보자.

2. 3×3 라틴 방진을 품은 8×8 라틴 방진을 만들 수 있을까? 가능하다면 만들어 보고, 불가능하다면 증명해 보자.

3. M×M 라틴 방진을 품은 N×N 라틴 방진을 만들 수 있는 N, M의 조건은 무엇일지 유추해 보자.

4. 위 조건을 만족하는 N과 M이 주어졌을 때, 어떤 규칙에 따라 수들을 배열해야 M×M 라틴 방진을 품은 N×N 라틴 방진을 만들 수 있을까? 만드는 방법은 무궁무진하니 자유롭게 규칙을 찾아 보자. 필자가 찾은 방법 중에는 N, M의 홀짝성에 따라 성립하지 않는 방법도 있었으니, 독자 여러분이 찾은 방법이 N, M의 홀짝을 고려한 4가지 경우에 모두 성립하는지 검증해 보면 도움이 될 것이다.