매월 정답자 한 분을 선정하여 고등과학원에서 문화상품권을 드립니다.
퍼즐 참여는 6월 27일까지 가능하며 다음달 초 해설과 함께 정답자가 공개됩니다.
(답안과 함께 이름, 연락처,메일 주소를 남겨주셔야 정답자 선정 연락이 가능합니다!)
클라인 병Klein Bottle은 독일의 수학자 Felix Klein(1849-1925)의 이름을 딴 곡면으로, 경계가 없지만 마치 뫼비우스 띠Möbius strip처럼 한 쪽 면밖에 존재하지 않는다. 4차원 공간상에는 제대로 그려낼 수가 있지만, 3차원 공간 내에 표현하려면 스스로를 교차하는 부분이 있도록 그려낼 수밖에 없다. 그렇게 만들어낸 모델 중 하나가 다음과 같이 병처럼 생겼기에 병Bottle이라고 불리게 되었다.
그런데, 동그란 구멍이 하나 뚫려 있는 클라인 병을 상상하면 그것은 3차원 공간 내에 온전히 그려낼 수 있다. 다음과 같이 그 뚫려 있는 구멍을 통해서 병의 주둥이가 바닥과 이어지도록 하면 되기 때문이다.
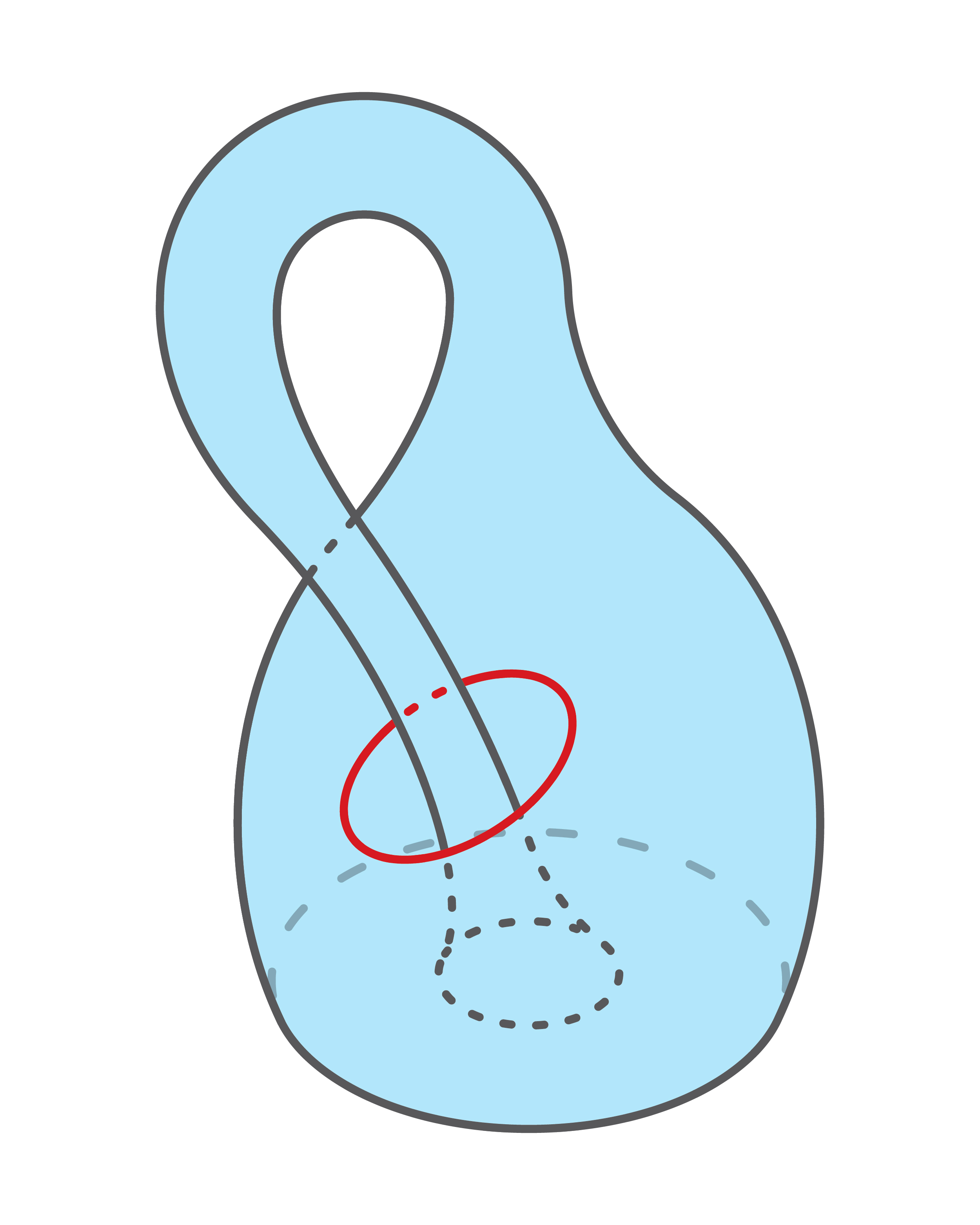
이렇게 구멍이 뚫린 클라인 병이 오늘의 주인공이다. 여기에 금속 고리가 (A)처럼 걸려 있다고 하자. 이 상태에서 클라인 병을 찢거나 붙이는 등의 조작 없이 변형해서 오른쪽의 (B) 상태로 만들려면 어떻게 해야 할까? 금속 고리는 변형할 수 없다고 가정하고, 클라인 병의 두께는 무시하며, 병의 재질이 무한히 신축성 있는 고무이기에 얼마든지 늘이거나 줄일 수 있다고 가정한다.
이 퍼즐은 이른바 “위상수학 퍼즐Topology Puzzle“이라고 불리는 퍼즐 갈래에 포함시킬 수 있다.