10월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
10월의 퍼즐 정답자 중 좋은 직관을 얻을 수 있는 풀이를 남겨주신 김규현님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
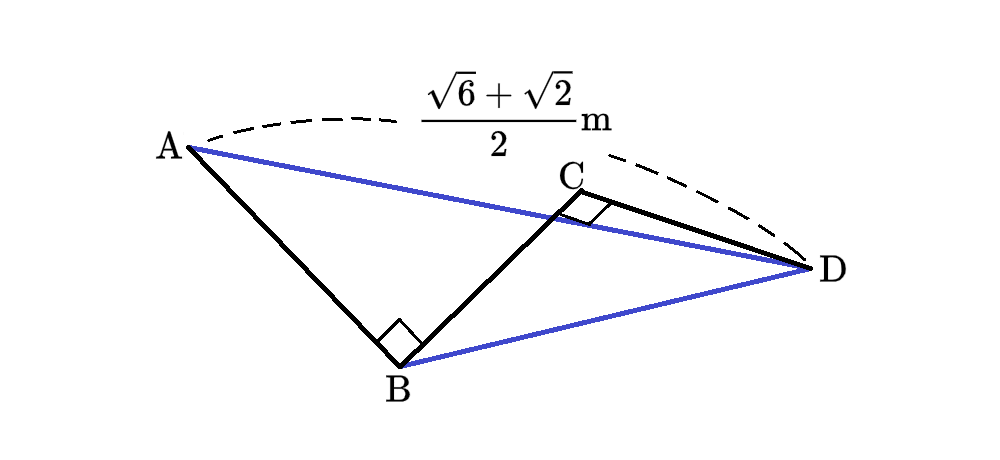
두 주황색 부품 간을 연결하는 데 쓰이는 봉이 1개이거나 2개이면 각각 거리가 1m, \(\sqrt{2}\)m로 고정되어 버린다. 그러니 주어진 길이만큼 벌리려면 일단 두 부품 사이에 봉이 3개가 이어져 연결되어 있어야 함을 알 수 있다. 봉을 3개만 준비해 와서 이어 조립하고, 양 끝을 \(\frac{\sqrt{6}+\sqrt{2}}{2}\)m 벌려 놓아 보자. 이 상황을 (약식으로) 그려보면 다음과 같이 된다.
여기서 공간상의 삼각형 ABD를 살펴보자. 선분 AB의 길이는 1m이고, 선분 BD의 길이는 (삼각형 BCD가 직각이등변삼각형이므로) \(\sqrt{2}\)m이다. 세 변의 길이를 모두 알았으니 코사인법칙을 쓸 수 있다. 각 BAD의 크기를 \(\alpha\)라고 하면,
\[\cos\alpha = \frac{1^2+\left(\frac{\sqrt{6}+\sqrt{2}}{2}\right)^2-\sqrt{2}^2}{2\cdot 1\cdot \frac{\sqrt{6}+\sqrt{2}}{2}} = \frac{1+\sqrt{3}}{\sqrt{6}+\sqrt{2}} = \frac{1}{\sqrt{2}}\]
이다. 즉 \(\alpha\)의 크기가 45도라는 이야기다. 그림이 대칭적이므로 이는 곧 각 CDA 또한 45도라는 점을 시사한다. 그러니, 똑같은 조립품을 하나 더 만들어온 뒤에 선분 AD 기준으로 180도 회전 대칭한 위치에 놓고 조립하면
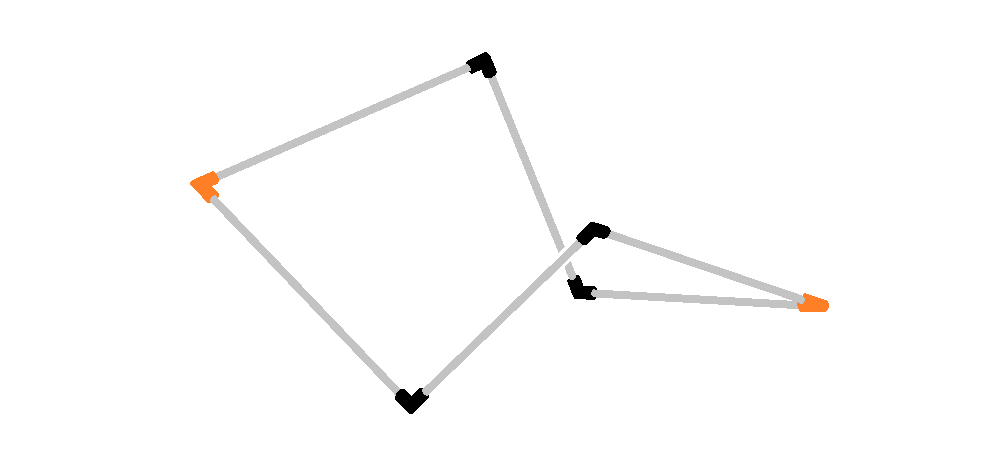
이렇게 원하던 구조물이 만들어진다.
번외로, 왜 \(\frac{\sqrt{6}+\sqrt{2}}{2}\)m이 최댓값인지 궁금한 독자들도 있을 것이다. 이를 추론하는 것은 어렵지 않다. 구조물을 공간상의 육각형 ABCDEF이라고 하고 주황색 부품이 있는 자리가 A와 D라고 하면, 선분 AC, CE, EA의 길이가 전부 \(\sqrt{2}\)m(직각이등변삼각형의 빗변)로 동일할 수밖에 없다. 따라서 삼각형 ACE는 정삼각형이며, 선분 CE의 중점을 M이라 할때 선분 AM의 길이는 \(\frac{\sqrt{6}}{2}\)m가 된다. 한편 삼각형 CDE가 직각이등변삼각혐임에서 우리는 선분 MD의 길이가 \(\frac{\sqrt{2}}{2}\)m임을 안다. 그러므로 삼각부등식에 의해 선분 AD의 길이는 두 길이를 합친 \(\frac{\sqrt{6}+\sqrt{2}}{2}\)m보다 작거나 같을 수밖에 없다.
사실 풀이에 쓰인 이 구조는 아주 흥미로워서 더 많은 이야기를 할 수 있다. 그 중 하나를 더 언급하면서 글을 마무리하려 한다. 철봉과 연결부가 이어진 곳이 윤활이 되어 있어 봉이 자유로이 회전할 수 있다고 가정하자. 그러면 문제 본문에도 그려져 있던 “ㄴ”자 모양의 구조를 만들고 난 뒤에, 그를 분해하지 않고 그대로 부드럽게 다른 “ㄴ”자 구조로 변형할 수 있다. 이 과정을 나타내면 다음과 같다. 빨간색 삼각형과 파란색 선분은 이전 문단에서 언급된 것들이다.
이 과정에 철봉이 휘는 일도 없고, 모든 순간 순간에 6개의 연결부 각도가 전부 90도로 잘 유지된다. 놀랍지 않은가? 이뿐만이 아니다. 변형 과정의 정중앙 시점에 파란 선분들이 일직선이 되는데, 그 상태가 정확히 문제의 정답이 되는 상태이다. 어째서 이런 일들이 가능한지 더 탐구해 보는 것은 독자의 몫으로 남긴다.
다음은 10월의 정답자로 선정된 김규현님의 해설입니다.
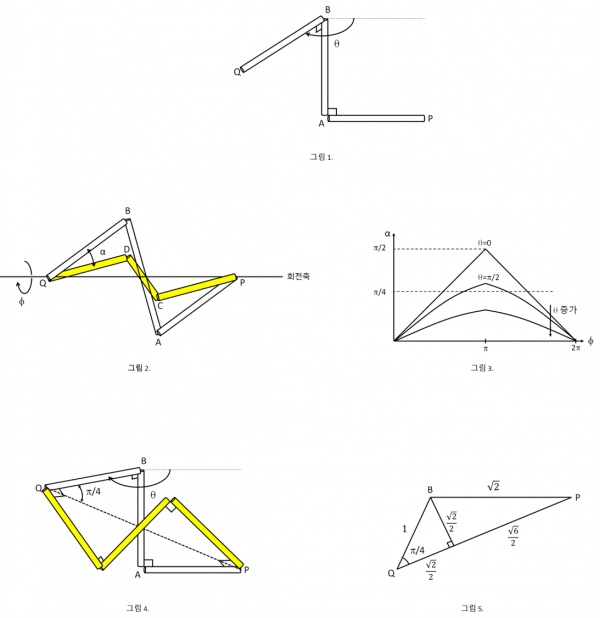
철봉 두 개를 사이에 둔 두 연결부 간의 거리는 항상 \(\sqrt{2}\)이므로, 주황색 연결부 사이에는 3개의 철봉이 있어야 한다. 전체 구조물의 반, 즉 철봉 3개의 구조는 [그림1]과 같이 단순화할 수 있다. 점 P와 Q를 주황색 연결부라고 가정하자. 철봉1(P-A)과 철봉2(A-B)를 [그림1]과 같이 고정했을 때, 철봉3(B-Q)은 1개의 자유도(즉, 철봉1(P-A)에 대한 회전각)를 가진다. 이 회전각을 θ라 할 때, P와 Q 사이의 거리는 θ의 함수이다. 다른 세 개의 철봉으로 이루어진 나머지 반쪽의 구조물도 가장 먼 연결부 간의 거리는 [그림1]의 P-Q 사이의 거리와 같아야 하므로, [그림1]의 구조와 동일한 구조 (즉 같은 θ)를 갖거나, [그림1]의 구조와 대칭적인 구조 (즉, -θ)를 가져야 한다. 이 중에서 대칭적인 구조는 생각하지 않아도 된다. (이유는 뒤에서 설명)
즉, 전체 구조물은 [그림1]의 동일한 반구조물 2개로 이루어진다. 두 개의 반구조물을 결합하기 위하여 [그림2]에서와 같이 반구조물 P-A-B-Q와 P-C-D-Q를 P와 Q에서 연결하고, 반구조물 P-A-B-Q는 고정시키고, 반구조물 P-C-D-Q는 P-Q를 회전축으로 하여 회전시킨다. 이때의 회전각을 φ라 할 때, P-A와 P-C 간의 각 및 B-Q와 D-Q 간의 각이 직각이 되어야만 조건을 만족한다. 두 반구조물이 동일한 구조이므로 각 CPA가 직긱이면 각 BQD도 직각이 된다. (두 반구조물이 서로 대칭이라면, 이것이 성립하지 않는다.)
각 CPA (=α)는 φ및 θ의 함수이며, 주어진 θ에 대해서 φ=[0,π]에서 단조증가, φ=[π,2π]에서 단조감소한다. α(φ)=π/2가 되는 φ일 때 조건을 만족하는 구조물이 된다.
그런데 PQ간의 거리는 θ가 클수록 크다 (0≤θ≤π). 따라서, α=π/2가 되는 φ가 존재하는 최대의 θ일 때 PQ간의 거리가 최대가 된다. 즉, α(π)=π/2가 구하는 조건이다. [그림4] 이때 ∠APQ = ∠CPQ= π/4이므로, [그림5]에서와 같이 이때의 PQ 간의 거리는 (\(\sqrt{6}\)+\(\sqrt{2}\))/2 이다.