[12월의 퍼즐 해설] 크리스마스 트리

문제1. \(n = 1, 2\)일 때는 각각 1가지밖에 없음을 쉽게 알 수 있다. 그러니 \(n \geq 3\)이라고 하자. 맨 위층을 제외한 각 층의 가장자리의 두 점들은 조건 3에 의해 바로 위층의 점과 연결되어야 하지만, 그러한 점이 하나밖에 없으므로 선택지가 하나밖에 없다. 하지만 나머지 \(\frac{(n-2)(n-1)}{2}\)개의 점들은 바로 위의 두 점 중 하나를 선택해서 변으로 연결할 수 있으며, 모든 점들에 대해서 선택을 수행하면 크리스마스 트리가 하나 만들어진다. 따라서 가짓수는
\[
2^\frac{(n-2)(n-1)}{2}
\]
이다. \(n = 1, 2\)일 때도 식의 값이 정답인 1이므로 이 식이 바로 원하던 식이다.

문제2. \(n = 1\)일 때 가짓수가 1임은 쉽게 안다. 그러니 \(n \geq 2\)라고 하자. 두 개의 연속된 층과 그 사이에 있는 변을 그리면

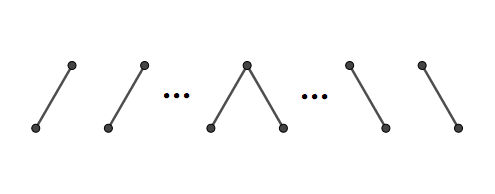와 같이 ‘/’자 모양의 변이 이어지다가 중간에 ‘\’ 모양의 변으로 바뀌고 그것이 끝까지 이어질 수밖에 없다. 그렇지 않을 경우, 순환을 만들지 않기 위해서는 반드시와 같은 경우가 중간에 포함될 수밖에 없는데, 상단 가운데에 있는 점 때문에 조건 4에 위배가 된다. 따라서, 각 층과 층 사이마다 어디서 ‘/’와 ‘\’ 사이의 전환이 일어날지만 정해지면 그것으로 안정적인 크리스마스 트리 하나가 결정이 되고, 가짓수는
\[
1\times 2\times\cdots\times(n-1) = (n-1)!
\]
이다. \(n = 1\)일 때도 식의 값이 정답인 1이므로 이 식이 바로 원하던 식이다.

문제3. 크기 \(n\)의 안정적인 크리스마스 트리는 앞서 구했듯 개수가 \((n-1)!\)가지이다. 또한 \(1, 2, …, n-1\)을 배열하는 순열의 가짓수도 정확히 \((n-1)!\)가지이다. 이 둘을 canonical하게 대응시키는 방법이 있다.

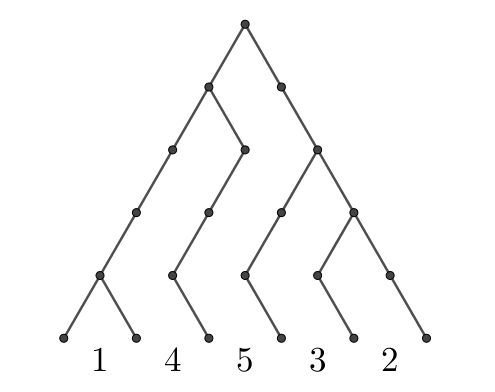
맨 밑층에 있는 \(n-1\)개의 공백에, 각 공백이 몇 칸씩 올라가서 닫히는지를 적어 넣으면 된다. 반드시 1부터 \(n-1\)까지가 전부 하나씩 나올 수밖에 없으며, 하나의 트리에 두 가지 이상의 순열이 대응될 수는 없다. 따라서 이 순열 하나가 안정적인 크리스마스 트리 하나와 정확히 대응된다.

두 안정적인 크리스마스 트리는 언제 동등해질까? 첫 번째 트리를 맨 위 꼭짓점에서 잘라 둘로 나눈 것을 각각 왼쪽에서 오른쪽으로 \(A\), \(B\)라 하고, 두 번째 트리를 그렇게 나눈 것을 \(A’\), \(B’\)이라 하자. 그러면 (동등한지를 따질 때 맨 위 꼭짓점은 맨 위 꼭짓점으로 대응시킨다 가정한다)

• \(A\)와 \(A’\)가 동등하고, \(B\)와 \(B’\)가 동등하다
• \(A\)와 \(B’\)가 동등하고, \(B\)와 \(A’\)가 동등하다

의 두 경우 중 하나이면 된다. \(n\)이 3 이상이므로 좌우대칭인 안정된 크리스마스 트리는 존재하지 않는다. 한 층에 분기점이 2개가 되는 경우가 생기기 때문이다. 그러니 여기서 두 번째 경우는 고려하지 않고 첫 번째 경우만 고려해서 개수를 구한 뒤 전체 수를 절반으로 나눠도 거울 대칭에 의해서 똑같은 결과를 얻게 된다. 그렇게 진행하도록 하자.

여기서 우리는 몇 가지 관찰을 할 수 있다. 트리를 순열로 표기할 때, \((p_1, \cdots, p_k, n-1, q_1, \cdots, q_{n-2-k})\)와 \((r_1, \cdots, r_l, n-1, s_1, \cdots, s_{n-2-l})\)이 첫 번째 경우로 동등하면,

• \(k = l\)이다
• \((r_1, \cdots, r_l)\)은 \((p_1, \cdots, p_k)\)의 재배열이다.
• \((s_1, \cdots, s_{n-2-l})\)은 \((q_1, \cdots, q_{n-2-k})\)의 재배열이다.

이뿐만이 아니다. \(p_i\)들을 크기순으로 재배열한 순열을 \((x_i)\)라고 하자. 그럼 \((p_1, \cdots, p_k)\)을 \((x_{\sigma(1)}, \cdots, x_{\sigma(k)})\)로 표기할 수 있고, 재배열이라는 조건을 사용하면 \((r_1, \cdots, r_l)\)을 \((x_{\tau(1)}, \cdots, x_{\tau(k)})\)로 표기할 수 있다. 여기서 다음 관찰까지 얻을 수 있다.

\(A\)와 \(A’\)가 동등하다 \(\Leftrightarrow\) \((\sigma(1), \cdots, \sigma(k))\)와 \((\tau(1), \cdots, \tau(k))\)가 동등하다.

여기서 오른쪽의 명제는 크기 \(k+1\)의 안정적인 크리스마스 트리로서의 동등함을 말하는 것이다. 이 관찰은, \(A\)에서 분기가 나눠지는 층을 제외한 모든 층을 압축시키는 작업을 수행하면 최후에는 크기 \(k+1\)의 안정적인 크리스마스 트리가 하나 나온다는 사실에 기반한다. 또한 방금의 관찰은 \(B\)와 \(B’\)가 동등한지 판정하는 데에도 그대로 적용할 수가 있다.

따라서 (첫 번째 경우로) 동등한 것을 제외한 크기 \(n\)의 크리스마스 트리는

1. 순열의 \(n-1\)개의 칸 중 숫자 \(n-1\)이 어디에 들어갈지 정한다.
2. \(n-1\)이 \(k+1\) 번째 칸에 들어갔다고 가정할 때, 그 앞의 \(k\)개의 숫자로 무엇이 들어갈지 (순서에 상관 없이) 정한다.
3. 크기 \(k+1\)의 안정적인 크리스마스 트리 \(a_{k+1}\)가지 중 하나를 골라서 그것과 대응되게 앞의 \(k\)개의 숫자를 배치한다.
4. 크기 \(n-1-k\)의 안정적인 크리스마스 트리 \(a_{n-1-k}\)가지 중 하나를 골라서 그것과 대응되게 앞의 \(n-2-k\)개의 숫자를 배치한다.
   
   

의 과정을 통해 하나로 정해진다. 또한 이 방법으로 모든 트리를 얻을 수 있으므로 이 4가지 과정을 통해 생기는 경우의 수를 모두 구하면 그것이 답이다. 이를 그대로 식으로 옮기면,

\[
\sum_{k=0}^{n-2}\binom{n-2}{k}a_{k+1}a_{n-1-k}
\]
이 된다. 앞서 언급한 대로 두 번째 경우의 동등까지 고려하여 전체를 반으로 나누고 index를 조금 고치면
\[
a_n = \frac{1}{2}\sum_{i=1}^{n-1}\binom{n-2}{i-1}a_{i}a_{n-i}
\]
을 얻는다.

참고로, 이 \(a_n\)은 OEIS에도 등록되어 있는 수열이다. 혹시 더 알아보고자 하는 독자들은 한번 들어가 보는 것도 좋을 듯하다.

임은성님이 보내주신 상세 페이지에서 좀 더 쉽게 보실 수 있습니다.