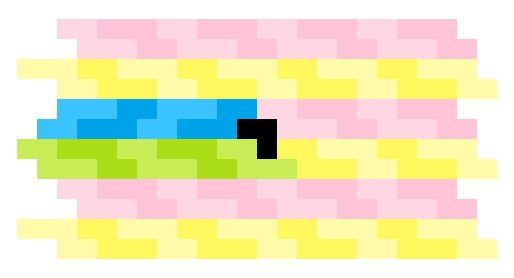[2월의 퍼즐 해설] 펜토미노로 구멍 뚫린 평면 채우기

모든 소문제는 2개 이상의 답을 가지고 있다. 어떤 접근법으로 접근했는가에 따라서 다양한 답이 나올 수 있다. 여기에서는 필자가 찾아낸 방법을 소개하겠지만, 독자들은 각자 다양한 방법과 답을 찾았을 것이다.

한 펜토미노를 무한히 이어붙여 선을 만든 다음, 그 선을 다시 다른 방향으로 무한히 이어 붙여 평면을 채울 수 있다면 결과적으로 펜토미노로 평면을 채울 수 있다. 아이디어는 여기에서 시작한다.

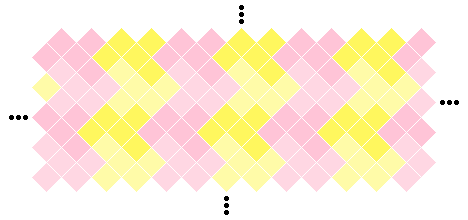
가령, F자 펜토미노를 보자. F자 펜토미노들을 잘 이어 붙여서 다음과 같은 무한히 긴 선을 만들 수 있다면, 이 선들을 다시 복사해서 평면을 채우는 건 일도 아니다.

이 선을 그대로 둔 모양과 180도 돌린 모양을 반복하면서 위아래로 늘어놓으면 간단히 평면이 채워지기 때문이다.

그리고 위 실루엣은 F자 펜토미노들을 다음과 같이 배치하여 만들 수 있다.

그러면 우리는 F자 펜토미노를 사용해 평면을 채우는 방법을 찾았다. 위에서 찾은 방법에 그대로 대입해 보면 아래와 같은 그림을 얻는다. 이는 구멍이 뚫리지 않은 평면을 F자 펜토미노로 빈틈없이 채우는 방법이다.

이제 다음이 중요하다. 위에서 찾은 선을 다른 방법으로 다시 만들 텐데, 이번에는 ㄱ자 모양 구멍이 남도록 딱 세 칸을 비워 놓고 만들 것이다. 아래와 같이 하면 가능하다.

이제 앞에서 한 것과 같이 선들을 무한히 이어 붙여 평면을 채우되, 선 중 딱 하나만 이렇게 구멍을 뚫은 선으로 대체하자. 그러면 ㄱ자 모양의 구멍이 뚫린 평면이 탄생한다.

위 예시에서는 3칸짜리 ㄱ자 구멍이 뚫린 선 하나를 썼지만, 1칸짜리 구멍이 뚫린 선과 2칸짜리 구멍이 뚫린 선을 하나씩 쓰는 것도 가능하다. 그러면 1칸짜리 구멍과 2칸짜리 구멍이 하나씩 뚫린 평면이 될 것인데, 그 두 구멍이 맞닿아 있다면 ㄱ자 구멍이 뚫린 평면을 만들 수 있다.

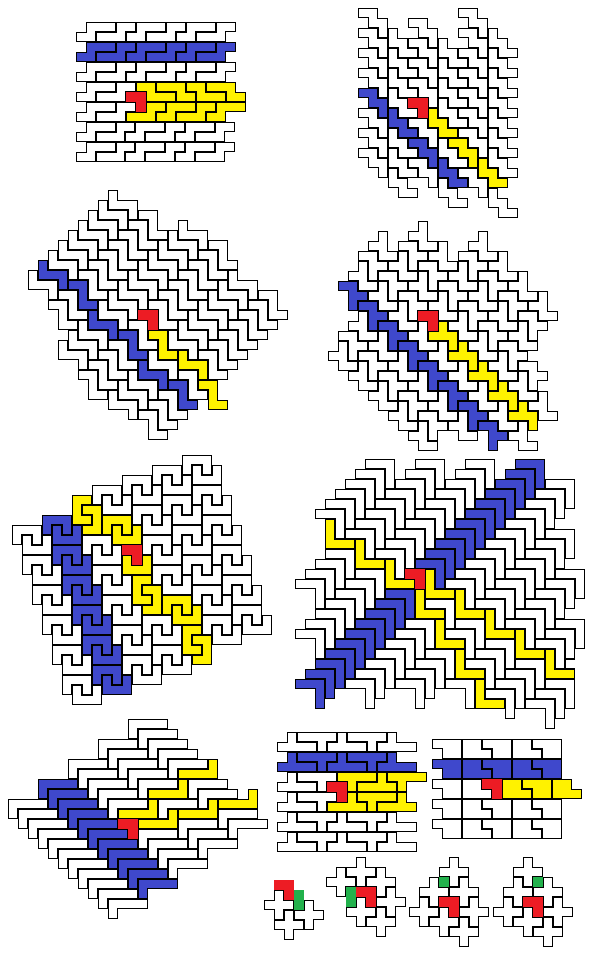
N자, W자, Z자, F자 펜토미노로 구멍 뚫린 평면을 채우는 방법은 위에서 소개한 방법으로 어렵지 않게 만들어낼 수 있다.

N자
(2칸짜리 구멍이 뚫린 선과 1칸짜리 구멍이 뚫린 선을 하나씩 썼음에 주목하자)

W자

Z자

F자 (위에서 소개한 답안이다)

V자 펜토미노에 대한 답안은 조금 더 어렵다. 앞에서 소개한 방법을 약간 시선을 바꿔서 재해석해 보자. 먼저 선을 만들고 그 선으로 다시 평면을 만드는 것은 똑같다. 그 다음에, 그 평면을 만들 때 쓴 선이 아니라 새로운 선을 몇 개 찾아낸다. 그리고 그걸 통째로 들어내고, 대신 그 자리에 꼭 맞도록 구멍이 뚫린 선들을 새로 제작해서 넣는 것이다. 여기서 선이라 함은 양쪽으로 무한한 직선이 아니라 한쪽으로만 무한한 반직선일 수도 있다. 이 방법을 이용하면 V자는 다음과 같이 만들 수 있다.

V자

파란색 펜토미노들이 선들을 들어내고 새로 끼워넣은 펜토미노들이다. 어떤 선을 들어내고 새로운 펜토미노들을 끼워넣었는지 알 수 있을 것이다.

U자 펜토미노는 위와 같은 접근법으로는 풀리지 않는다. U자 펜토미노로 평면을 채운 다음 반으로 갈랐다가 어긋나게 합쳐서 공간을 만드는 방식을 사용해볼 수 있다.

U자

먼저 주어진 그림을 보면 붉은색 펜토미노들만 보면 1. 무한한 평면을 가득 채우는 모양이며 푸른색은 2. ㄱ자 구멍에 의해 생기는 반복되는 변형이다.

이에 따라 다른 펜토미노로 ㄱ자 구멍을 남기고 평면을 채우기 위해서는 1. 먼저 무한한 평면을 가득 채우는 모양들을 찾고 2. ㄱ자 구멍을 추가하여 반복 가능한 변형을 가해야 한다.

그림에서 푸른색 펜토미노들은 1. 무한한 평면을 채우는 모양을 나타내며 노란색 펜토미노들은 2. 붉은 ㄱ자 구멍에 의해 생기는 반복가능한 변형이다.

추가적으로 X 펜토미노의 경우에는 ㄱ자 구멍 주변을 둘러서 덮는다고 하면 모든 경우에 초록색의 덮을 수 없는 영역이 생기기 때문에 ㄱ자 구멍만 남기고 무한한 평면을 가득 채울 수 없다.