2022 필즈상 수상자 마리나 비야조우스카: 8차원과 24차원의 기적

어떤 자연수로 이루어진 수열이 있다. 처음에는 1, 2, 3으로 시작하기에 당연히 다음에 4가 나올 것이라 기대하게 되지만, 그다음에 오는 숫자는 이상하게도 8이다. 그리고 그다음은 더 기이하게도 24이다. 1, 2, 3, 8, 그리고 24. 이들은 지금 이 순간 인류가 공간을 가장 밀도 높게 공으로 채우는 방법을 알고 있는 차원의 목록이다. 2016년 이전까지 이 기묘한 수열은 1, 2, 3에서 멈춰있었다.

2016년 3월 아카이브^arXiv라는 수학 논문 웹사이트에 우크라이나 출신의 여성 수학자 마리나 비야조우스카^{Maryna Viazovska}의 스무 페이지가량의 논문이 하나 올라왔다.[1] 논문의 제목은 ‘8차원에서의 공 채우기 문제’. 이 논문은 \(E_8\)이라 불리는 격자가 8차원 공간을 공으로 가장 밀도 높게 채우는 방법이라는 사실의 증명을 담고 있었다. 불과 일주일 뒤 비야조우스카와 헨리 콘^{Henry Cohn}, 아브히나브 쿠마르^{Abhinav Kumar}, 스티븐 밀러^{Stephen D. Miller}, 다닐로 라드첸코^{Danylo Radchenko} 다섯 명의 수학자가 힘을 합쳐 24차원의 공 채우기 문제를 해결한 논문이 아카이브에 올라오게 된다.[2] 두 논문은 이듬해 수학연보^{Annals of Mathematics}라는 권위 있는 수학 저널에 동시에 나란히 실리게 된다. 공 채우기 문제에 대한 이정표와 같은 결과가 언제나 그래왔듯이.

2022년 7월, 비야조우스카는 고차원의 공 채우기에 대한 결과와 후속 연구의 중요성을 인정받아 필즈상을 수상하였다. 지난 2014년 서울에서 필즈상을 수상한 마리암 미르자하니^{Maryam Mirzakhani}에 이어 두 번째 여성 수상자가 되었다. 2022년 세계수학자대회는 러시아에서 개최될 예정이었다. 그러나 그해 2월의 러시아의 우크라이나 침공은 수학자 공동체에 공분을 일으켰고, 러시아에서 열리는 수학자대회에 대한 보이콧 선언이 여기저기서 터져 나오게 된다. 결국 국제수학연맹은 대회를 온라인 행사로 변경하기로 결정한다. 그러한 연유로 핀란드에서 열리게 된 시상식에서 우크라이나 수학자가 필즈상을 받는 장면은 매우 극적인 것이기도 했다.

^영상 2022 필즈상 수상자 마리나 비야조우스카 / IMU

구 채우기 문제

구 채우기^{sphere packing}는 오랜 역사를 가진 수학 문제이다. 케플러의 추측이라는 이름으로도 널리 알려져 있으며 비교적 간단하게 설명할 수 있는 문제이기도 하다. 상자가 주어져 있고, 그 안에 똑같은 크기의 단단한 공을 가능하면 많이 넣으려고 한다. 상자의 모양이 제각각이라면 공의 크기도 고려해야 하고 답도 제각각이 될 것이다. 문제를 더 간단히 만들기 위해 상자의 크기는 무한히 크다고 가정한다면, 가장 밀도 높은 배열은 과연 무엇일까?

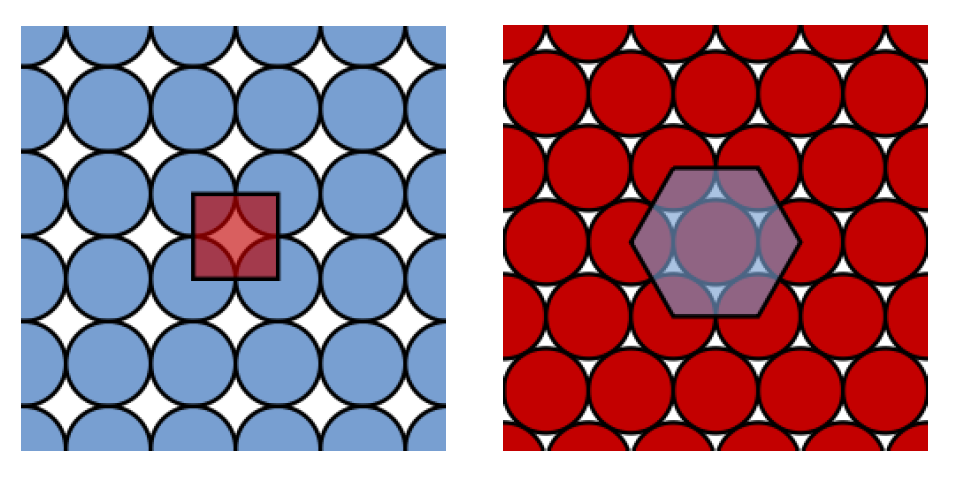
쉬운 상황을 먼저 생각해 보자. 2차원에서 이 문제는 넓은 평면에 같은 크기의 동전을 밀도 높게 배열하는 것으로 이해할 수 있다. 다음과 같은 모양으로 동전을 배열한다고 해 보자. ([그림1])

동전 사이사이에 동전으로 덮이지 않는 영역을 가능하면 줄여야 밀도 높은 배열이라 할 것이다. 동전이 얼마나 밀도 높게 배열되었는지의 여부는, 전체 영역에서 동전이 덮는 영역의 넓이의 비율로 따지는 것이 적절할 것이다. 이 경우는 배열이 주기적이므로, 그림에서처럼 하나의 정사각형이 원에 의해 얼마나 덮여 있는지 생각하면 된다. 이것은 이제 초등학교의 수학책에서 흔히 볼 수 있는 넓이 문제가 되었다. 이 경우 채우기의 밀도는 \(\pi/4\)로, 약 78.54%가 된다.

실제로 동전을 가지고 놀면서 실험을 해 본다면 어렵지 않게 벌집처럼 하나의 동전을 여섯 개의 동전이 둘러싸고 있는 조밀한 배열을 발견하게 될 것이다. ([그림2])

이 경우는 동전이 덮는 영역이 차지하는 넓이의 비율이 \(\pi/\sqrt{12}\), 즉 90.69% 정도가 된다. 사각형 형태의 배열보다 훨씬 밀도가 높아진다. 그리고 자연스럽게 이것이 가장 밀도가 높은 배열이라고 생각하게 된다. 하지만 이것이 모든 동전의 배열 중에서 가장 공간을 낭비하지 않는 방법이라는 사실을 증명하는 것은 그리 간단하지는 않다. 동전을 배열하는 무한히 많은 방법을 모두 고려해서 서로 비교하는 일이 간단하지 않기 때문이다. 이 사실에 대한 증명은 19세기 말 튜에^{Axel Thue}에 의해 얻어졌다.[3]

1600년대 초 케플러는 육각형 눈송이에 대한 에세이에서 3차원 공간에서 같은 크기의 공을 가장 밀도 높게 쌓는 방법에 대한 추측을 남겼다. 그런 방법이란 사실 매우 놀라운 것은 아니다. 과일가게와 같은 일상의 장소에서도 흔히 찾아볼 수 있는 것이기 때문이다.

맨 아래의 첫 번째 층은 2차원에서의 해법을 빌려와 정육각형 형태로 공들을 배열한다. 이제 세 개의 공이 만나는 곳 사이사이의 움푹 파인 곳에 공을 두는 방식으로 새로운 층을 쌓을 수 있을 것이다. 이런 방식으로 공을 한층 한층 쌓아 올리면 밀도가 \(\pi/\sqrt{18} \approx 0.7405\)이 되는데, 이것이 3차원에서 얻을 수 있는 가장 높은 밀도라는 것이 케플러의 추측이다.

이 추측은 제시된 이후 거의 400년 정도가 지난 1998년이 되어 토머스 헤일스^{Thomas C. Hales}가 증명하는 데 성공한다.[4] 그러나 그의 증명은 처음 공개된 이후 오랜 심사 과정과 논란의 시간을 거치게 된다. 증명이 길고 난해한 데다가, 컴퓨터가 결정적으로 이용되었다는 점이 많은 수학자를 만족시키지 못했기 때문이다. 이 결과는 7년이 지난 2005년에야 수학연보에 출판되었다. 비야조우스카의 8차원 공 쌓기에 대한 짧은 증명이 거의 즉각적으로 수학계에 받아들여진 점과 대조적이다. 3차원 케플러 추측의 증명은 4색 정리와 함께 중요한 수학적 결과가 컴퓨터를 이용해 증명된 사례로 유명하다.

수학자는 4차원, 5차원, 6차원의 세계도 상상하고, 그러한 세계에 있는 공도 생각한다. 학창 시절에 우리는 평면, 즉 2차원 유클리드 공간의 점 하나를 두 개의 실수를 이용하여 \((x,y)\)와 같은 식으로 나타내는 방법을 공부한다. 좌표를 이용하면, 원점을 중심으로 갖는 반지름이 1인 원은 \(x^2+y^2=1\)과 같은 방정식을 이용해 이해할 수 있다. 이는 고차원으로도 확장된다. 차원이 \(d\)인 유클리드 공간의 점은 \(d\)개의 좌표를 이용하여 \((x_1,\dots, x_d)\)와 같은 방식으로 나타낼 수 있고, 이 공간에서 원점을 중심으로 갖는 반지름 1인 구면은 \(x_1^2+\dots+x_d^2=1\)와 같은 식으로 표현할 수 있다. 물론 이런 고차원의 세계는 누구에게도 눈에 보이지 않는다. 하지만 수학자들은 그런 세계의 존재가 눈앞에 있는 사물의 존재보다 더 확실하게 믿을 수 있는 것이라고 생각하는 사람들인지도 모른다. 그러니 헤일스가 3차원 케플러의 추측을 증명한 후에도, 고차원의 공 채우기라는 무한히 많은 문제가 수학자들에게 숙제로 남아있었다.

3차원에서 보았듯이, 문제의 단순함에도 불구하고 고차원에서의 구 채우기 문제에 대한 답을 찾기는 매우 어렵다. 차원을 높여가며 마주치게 되는 조밀한 구 채우기의 배열들 사이에 일정한 패턴을 찾기도 어렵다. 이는 각 차원에서의 공 채우기 문제가 제각각 다른 문제임을 암시한다. 3차원에서의 풀이를 적당히 변형해, 4차원 문제를 푸는 식의 접근이 잘 통하지 않는다는 말이다.

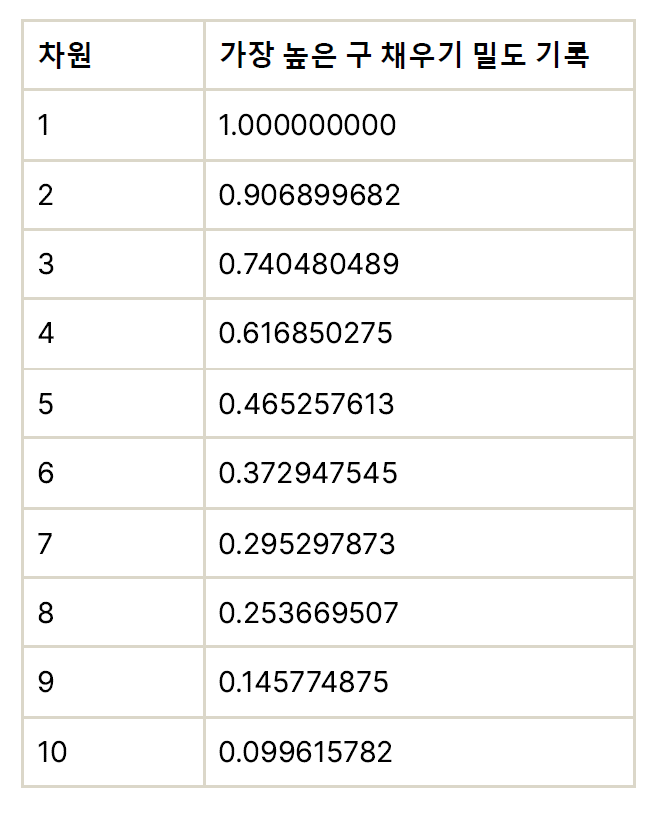
지금까지 알려진 가장 조밀한 공 채우기의 밀도는 10차원까지 다음과 같다[5]:

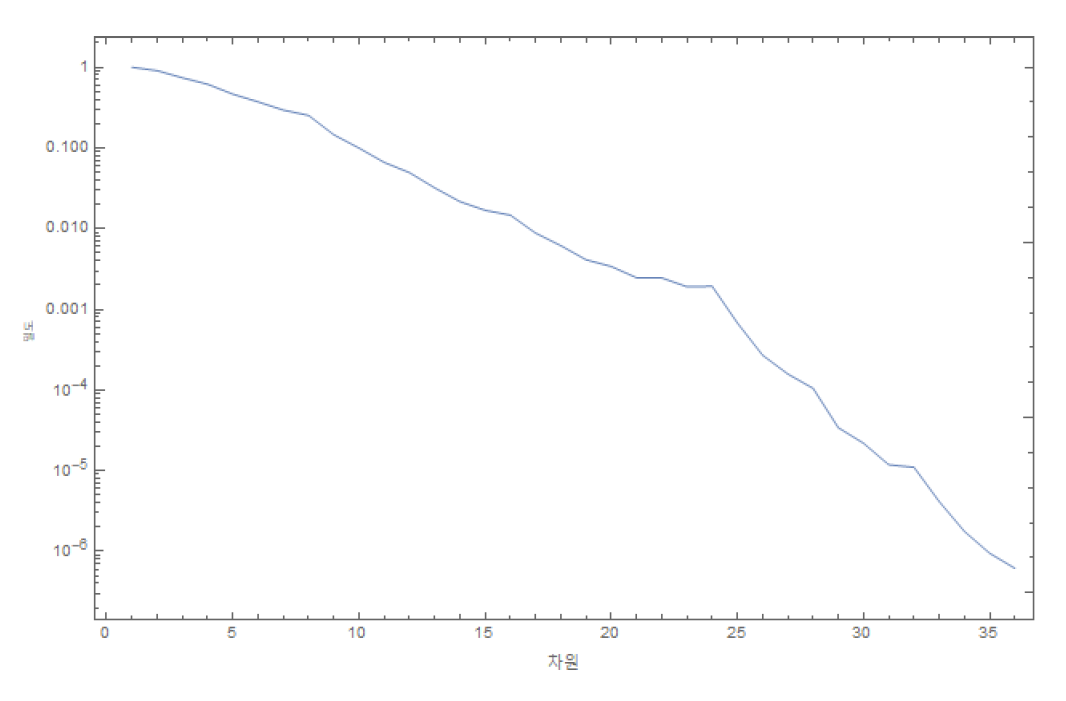
밀도는 차원이 커짐에 따라 지수적으로 빠르게 감소하는데, 밀도의 로그값을 이용해 그래프를 그리면 다음과 같다. ([그림4])

차원이 커지면서 밀도가 빠르게 감소하는 일반적인 경향성은 그래프에서 잘 드러난다. 그러나 8차원이나 24차원 부근에서는 약간의 불규칙성을 관찰할 수 있는데, 그 부근에서 그래프가 살짝 위쪽으로 당겨진 듯한 모습을 하고 있다. 여기엔 어떤 이유가 있을까?

수학의 예외적 구조들 그리고 \(E_8\)과 리치 격자

정삼각형, 정사각형, 정오각형으로 시작하는 정다각형의 목록에는 끝이 없다. 하지만 3차원에서 이에 대응되는 개념인 정다면체는 그렇지 않다. 3차원 공간에 살고 있는 정다면체는 오직 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체뿐이다. 2차원에는 무한히 많은 정다각형이 존재하지만, 3차원의 정다면체는 다섯 개밖에 없다. 이들은 학창 시절의 수학에서 접할 수 있는 진귀한 수학적 대상이라 할만하다. 정다면체의 대칭적인 형태와 이러한 희박한 존재성에는 어떤 마법적인 힘이 있는 듯, 시대를 뛰어넘어 수많은 사람들이 여기에 매료되어 왔다. 플라톤, 케플러, 데카르트 등이 그러한 사람들이며, 정다면체는 플라토닉 솔리드라고도 불린다. 서양의 역사에서 정다면체는 수학을 넘어 문화 전반에 상상력과 영감을 제공하며 영향력을 행사해 왔는데, ‘제5원소^quintessence‘라는 단어도 다섯 개 정다면체의 존재와 얽혀있다.

수학에서의 예외적인 구조란 이렇듯 어떤 면에서 희귀한 수학적 대상을 칭하는 말이다. 이들은 종종 특별한 성질이나 대칭성을 가지고 있어서 수학자들에게 흥미롭게 여겨진다. 조지 오웰의 풍자 소설 『동물농장』에는 ‘모든 동물은 평등하나, 어떤 동물들은 더욱 평등하다’라는 유명한 구절이 등장한다. 이 문장을 우리는 수학의 예외적인 구조에 대해 얘기할 때 활용할 수 있다. 가령, ‘모든 다면체는 평등하나, 정다면체는 더욱 평등하다’고 할 수 있다. 그리고 모든 격자는 평등하나, \(E_8\) 격자와 리치 격자와 같은 격자는 더욱 평등하다고 말할 수 있다. 콘웨이와 슬론은 구 채우기에 대한 고전 [5]의 서문에서 이 두 격자는 너무나 흥미로운 성질이 많아서 ‘…은 놀라운 사실이다’는 의미의 ‘It is a remarkable fact that’라는 영어 표현에 대한 축약어를 만들어 사용할지 고민했다고 농담처럼 적고 있다.

\(E_8\) 격자는 8차원 유클리드 공간에 살고 있다. 8개의 좌표가 모두 정수이거나, 모든 좌표가 정수에 \(1/2\)을 더한 꼴의 점 중에서 좌표의 합이 짝수가 되는 점들이 \(E_8\) 격자를 이룬다. 수식으로는 다음과 같이 쓸 수 있다:
\[
\left\{(x_i) \in \mathbb Z^8 \cup (\mathbb Z + \tfrac{1}{2})^8 : \sum_i x_i \equiv 0,\ \pmod 2\right\}.
\]
\(E_8\) 격자의 한 점과 원점에서의 거리를 제곱하면 모두 짝수인 정수가 된다. 또한 격자의 단위 영역^{fundamental domain}의 부피는 1이다. 이런 격자를 짝 유니모듈러 격자^{even unimodular lattice}라 하는데, 이런 격자는 8의 배수 차원에서만 존재할 수 있으며, 8차원에는 \(E_8\)이 유일하다.

이 격자에서 원점에서 가장 가까운 거리에 있는 점들은 240개이다. 다시 말해, 격자점을 중심으로 이용해 8차원 공간을 공으로 채운다면 하나의 공 주변을 240개가 둘러싸고 있는 형태가 된다. 그 본래의 모습을 눈으로 직접 볼 수는 없지만, 사용할 수 있는 하나의 방법은 이들을 적당한 평면에 투영하여 그림자를 보는 것이다. ([그림5])

이것이 원점 주위의 240개 격자점이 8차원에서 내려온 그림자이다. 2차원에서 조밀한 공 채우기 문제의 해답을 주는 정육각형 형태는 종종 눈송이에 비유된다. 평면에서 정육각형의 대칭적 형태를 유지하는 회전과 반사와 같은 직교변환^{orthogonal transform}이 12개라면, 8차원 공간의 직교변환 중에서 \(E_8\)의 형태를 보존하는 변환은 696,729,600개에 이른다. 이는 \(E_8\)이 3차원 공간의 정다면체처럼 매우 대칭적인 수학적 대상임을 말한다. 그렇다면 \(E_8\)은 8차원의 눈송이라 할만하지 않을까?

비야조우스카의 증명 이전에도 수학자들은 오랜 시간 8차원에서 가장 조밀한 구 채우기가 \(E_8\) 격자에 의해 주어질 것이라 믿어 왔다. \(E_8\)은 또한 8차원에서 하나의 공 주변에 가장 많은 공을 접하도록 하는 방법에 대한 해답을 주기도 한다. 가령 2차원에서는 하나의 동전 주변에 최대 6개의 동전을 접하게 만들 수 있다. 3차원에서는 최대 12개까지 가능하다. 이는 입맞춤 수^{kissing number}라 불리는데 8차원에서의 답은 240이 된다.

24차원 공간에 살고 있는 리치 격자^{Leech lattice}는 \(E_8\)과 마찬가지로 짝 유니모듈러 격자이다. 24차원에는 그러한 격자가 24개 존재하며, 리치 격자는 그중에서 원점에서의 거리가 \(\sqrt{2}\)인 점을 갖지 않는 유일한 격자이다. 리치 격자 역시 매우 풍부한 대칭성을 가지고 있다. 24차원에서 입맞춤 수 문제의 답 196560을 주며, 가장 조밀한 구 채우기의 방법이라 여겨져 왔다.

수학에서 잘 알려진 예외적인 구조의 다른 예로는 예외적인 리 대수^{exceptional Lie algebra}라 불리는 것이 있다. 이들은 큰 계열을 이루는 고전적인 리 대수와 구별되어, 각각 \(G_2\), \(F_4\), \(E_6\), \(E_7\), \(E_8\)라는 이름을 가지고 있다. 앞서 살펴본 \(E_8\) 격자는 여기서도 중요하게 등장한다. 또 다른 예외적인 구조로 산재군^{sporadic group}을 들 수 있다. 거의 모든 유한단순군은 몇 개의 큰 계열에 속하는데, 이들은 그러한 계열에 속하지 않는 26개의 예외를 일컫는 말이다. 이중 유명한 것으로 몬스터 군^{monster group}이 있다. 리치 격자는 이 몬스터 군과도 깊은 관계를 맺고 있으며, 리치 격자의 대칭성은 산재군의 연구 전반에 매우 중요하다.

콘과 엘키스가 찾아낸 전략

비야조우스카의 8차원의 구 채우기에 대한 작업은 2003년 수학연보에 출판된 헨리 콘과 노엄 엘키스^{Noam Elkies}의 논문 [6]에 기반을 두고 있다. 구 채우기 문제 자체는 기하학적이지만, 콘과 엘키스는 이 논문에서 특정한 성질을 만족하는 함수를 찾는 것이 구 채우기 문제에 큰 도움이 된다는 것을 보여주었다. 구 채우기가 이산적이며 기하학적인 세계에 속한다면, 여기 등장하는 함수들은 연속적이며 해석학의 세계에 속하는 수학적 대상이다. 이렇게 서로 다른 수학 사이의 깊은 상호작용은 수학의 역사에서 끊임없이 새로운 형태로 등장한다.

일반적인 고차원에서는 가장 조밀한 구 채우기가 어떠한지도 모르고, 그때의 밀도가 얼마인지도 알지 못한다. 하지만 콘과 엘키스는 선형 계획법이라 불리는 기법을 구 채우기 문제에 적용하여, 최적의 구 채우기가 갖는 밀도에 대한 상한을 얻는 방법을 제시하였다. 최적의 밀도에 대한 상한을 알면 어떤 구 채우기의 밀도도 그보다는 클 수 없다는 것을 알게 된다. 가령 4차원에서 그들의 방법으로 얻어진 밀도의 상한은 0.6477 정도이다. 4차원에서 알려진 가장 조밀한 구 채우기의 밀도는 대략 0.6169이다. 이 두 값이 서로 가까워질수록, 가장 조밀한 구 채우기의 이해에 더 가까워진다.

콘과 엘키스의 방법을 따르면 밀도의 상한을 얻기 위해 특정한 부등식을 만족시키는 함수를 찾아야 한다. 함수 \(f\)에 대한 부등식뿐만 아니라 그 함수의 푸리에 변환이라 불리는 함수 \(\widehat{f}\)도 어떤 부등식을 충족해야 한다. 좀 더 정확하게는 다음과 같이 서술할 수 있다 :

함수 \(f \colon \mathbb R^d \to \mathbb R\)는 우함수^even인 슈바르츠 함수이고 \(r\)은 양의 실수라고 하자. 여기서 \(f\)가 다음의 조건을 만족한다고 하자:

1. (1) \(|x| \ge r\)을 만족하는 모든 \(x \in \mathbb R^d\)에 대하여, \(f(x) \le 0\)

2. 모든 \(y \in \mathbb R^d\)에 대하여 \(\widehat{f}(y) \ge 0\)

3. \(f(0)=\widehat{f}(0)=1\)

그러면 \(\mathbb R^d\)에서 최적의 구 채우기 밀도는 최대 \(\pi^{d/2} (r/2)^d/\Gamma(d/2+1)\)이다.

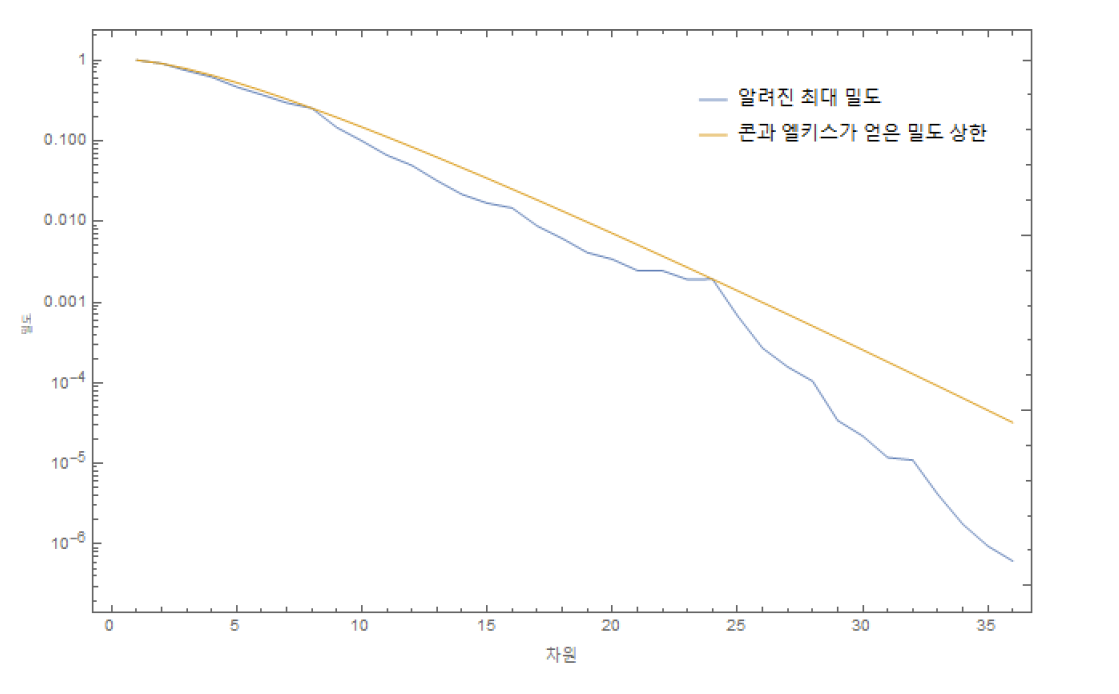
이 정리의 조건을 만족하는 함수 \(f\)를 하나 찾아내면 구 채우기 밀도의 상한을 얻게 된다. 그런 함수를 많이 찾아내면 운동 경기에서 기록을 경신하듯 상한의 크기를 낮춰갈 수 있다. 콘과 엘키스는 이 방법을 적용하여 36차원까지의 구 채우기의 밀도에 대한 새로운 상한을 얻었다. 다음은 차원을 \(x\)-축으로 하여 이 값들을 그래프로 나타낸 것이다. ([그림6])

그림에서 위에 놓인 선은 콘과 엘키스가 찾아낸 밀도의 상한이고, 아래의 선은 지금까지 알려진 가장 조밀한 구 채우기의 밀도이다. 실제로 가장 조밀한 구 채우기의 밀도는 두 선 사이의 어딘가에 위치하게 된다. 그래프는 콘과 엘키스의 방법으로 얻어지는 상한이 일반적으로 최적의 밀도와는 꽤 차이가 있음을 보여준다.

하지만 매우 흥미로운 점도 관찰할 수 있다. 차원 \(d\)의 값이 8과 24인 곳에선 두 선이 거의 붙어있다. 다시 말해 8차원과 24차원에서 그들이 얻은 상한은 8차원의 \(E_8\) 격자와 24차원의 리치 격자로부터 얻어지는 구 채우기의 밀도에 거의 근접한다. 이것은 8차원과 24차원에서 최적의 구 채우기의 해답이 \(E_8\) 격자와 리치 격자로부터 얻어짐을 강하게 뒷받침하는 동시에, 완벽한 증명에 대한 희망을 준다. 8차원의 경우라면 위에 서술한 콘과 엘키스의 정리에서 \(d=8\), \(r=\sqrt{2}\)로 두고 세 조건을 만족하는 함수 \(f\)를 찾아낼 수 있다면 증명이 끝난다. 24차원의 경우엔 \(d=24\), \(r=2\)로 두고 조건을 만족하는 함수를 찾으면 된다. 물론 그런 함수가 실제로 존재하는지의 여부는 모른다. 하지만, 이 그래프는 그런 함수의 존재성을 강력하게 지지한다. 그렇기에 콘과 엘키스는 훗날 사람들이 흔히 ‘마법의 함수’라 부르게 되는 8차원과 24차원의 공 채우기 문제를 해결해 주는 함수가 존재하리라 추측했다.

마법의 함수를 찾아서

콘과 엘키스의 결과에 의해 8차원과 24차원의 구 채우기 문제는 거의 해결된 것처럼 보였다. 콘은 당시에 문제를 마무리 짓지 못한 상태에서 다른 사람이 쉽게 답을 찾지 않을까 걱정했다고 회고한다.[7] 마법의 함수를 찾기만 하면, 수학의 역사에 이정표로 남을 증명을 얻는다는 점에서 이러한 조바심은 어렵지 않게 이해할 수 있다. 하지만 누구도 그러한 함수를 찾지 못한 채로 오랜 시간이 흐르게 된다. 그리고 콘은 이제 누구도 이것을 찾지 못할 것을 걱정했다고 전한다.

콘과 엘키스의 정리는 특정한 조건을 만족하는 함수가 존재할 때의 결론에 대해서 말해주지만, 그러한 함수를 어떻게 찾을 것인가에 대해서는 말해주지 않는다. 하지만 어렵지 않게 얻어낼 수 있는 몇 가지 추가적인 조건들은 있다. 가령, 8차원의 마법의 함수 \(f\)라면 다음과 같은 조건을 덧붙일 수 있었다:

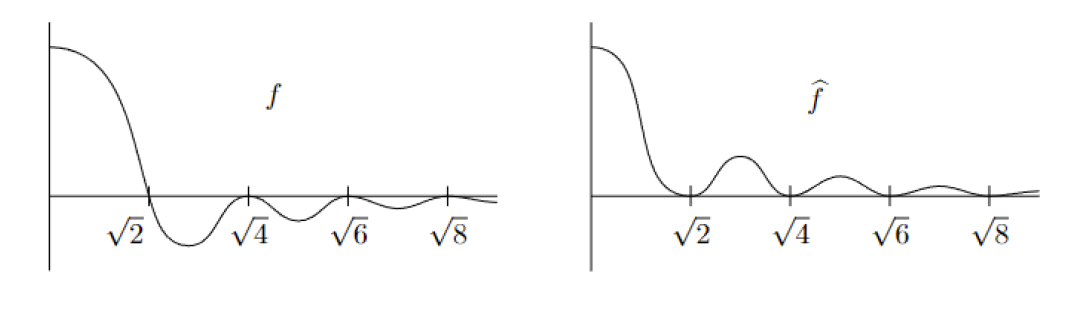
1. \(f(x)\)는 \(x\)의 길이, 즉 \(|x|\)에만 의존한다.
2. 점 \(x\in \mathbb R^8\)가 정수 \(k\geq 1\)에 대해 \(|x|=\sqrt{2k}\)를 만족하면, \(f(x)=\widehat{f}(x)=0\)이다.

그렇다면 \(f\)는 본질적으로 실수에 대해 정의되는 하나의 변수를 갖는 함수가 된다. 1변수 함수로서의 \(f\)와 \(\widehat{f}\)는 대략 다음과 같은 꼴의 그래프를 가져야 한다:

문제의 근본적인 어려움은 함수와 그 푸리에 변환을 동시에 다루는 일이 어렵다는 사실에 있었다.

비야조우스카가 해낸 일이 바로 8차원에서 이 마법의 함수를 명확하게 찾아낸 것이다. 1차원에서 \(x=\sqrt{2k},\, k=1,2,3,\dots\)의 위치에서 모두 0이 되면서 그래프가 위에서와 비슷한 꼴이 되는 마법의 함수 \(f\)를 만들어 내기 위하여, 그는 대담하게
\[
f(x) = \sin\big(\pi |x|^2/2\big)^2 \int_0^\infty A(t) e^{-\pi |x|^2 t} \, dt
\]
와 같은 형태의 함수를 탐색하기 시작한다. 이렇게 하면 일단 원하는 위치에서 함수가 0이 되도록 만들 수 있다. 물론 진짜 문제는 이 함수가 마법의 함수가 되도록 하는 적분 기호 안의 함수 \(A\)를 찾는 것이다.

그리고 이 탐색의 여정은 누구도 기대하지 않았던 놀라운 곳으로 향한다. 그는 적분 속의 함수를 정수론에서 보형 형식^{modular form}이라 불리는 함수를 사용하여 만들어 나간다. 이들은 매우 풍부한 대칭성을 가진 함수로, 페르마의 마지막 정리와 같은 문제의 해결에도 등장하는 현대수학의 매우 중요한 주제이다. 하지만 보형 형식이 이런 곳에서 등장할 것이라고는 이전엔 아무도 알지 못했다.

고전적인 수학의 장인과 같은 솜씨와 구석구석 새로운 아이디어를 결합해 그가 마침내 찾아낸 마법의 함수 \(f\)는 다음과 같은 모습을 하고 있다:
\[
f(x) = \frac{\pi i}{8640} a(|x|) + \frac{i}{240\pi} b(|x|).
\]
여기서
\[
a(r) = -4 \sin(\pi r^2/2)^2 \int_0^{i \infty} \phi_{0}(-1/z) z^{2} e^{\pi i r^2 z} \, dz,
\]
\[
b(r) = -4 \sin(\pi r^2/2)^2 \int_0^{i\infty} \psi_{I}(z) e^{\pi i r^2 z} \, dz,
\]
\[
\phi_{0} = \frac{1728 (E_2E_4 – E_6)^2}{E_4^3-E_6^2},
\]
\[
\psi_{I}=128 \frac{\theta_{00}^{4}+\theta_{01}^{4}}{\theta_{10}^{8}}+128 \frac{\theta_{01}^{4}-\theta_{10}^{4}}{\theta_{00}^{8}}.
\]

위에서 \(E_k\), \(\theta\)와 같은 기호로 등장하는 함수들이, 보형 형식의 이론을 공부하기 시작하면 머지않아 마주하게 되는 아이젠슈타인 급수, 세타 함수라는 이름을 가진 함수들이다. 오랜 시간 수학자들이 찾아 헤맨 마법의 함수의 구체적인 모습을 잠시나마 감상해 보는 것도 의미 있다고 여겨져 수식을 나열해 보았다.

맺음말

비야조우스카가 8차원에서의 공 채우기를 해결한 방식은 큰 변화 없이 24차원의 가장 조밀한 공 채우기가 리치 격자에 의해 얻어진다는 사실의 증명에도 적용된다. 비야조우스카는 증명에 사용된 아이디어를 더 발전시켜, 푸리에 보간법^{Fourier interpolation}이라는 주제의 새로운 일반적인 결과를 얻었다. 이는 함수와 그 푸리에 변환이 만족해야 하는 이산적 조건이 주어진 상태에서 그런 함수를 명시적으로 만들어 내는 방법에 대한 것이다.[8,9] 이후 물리학자들은 2차원 등각장론에 대한 부트스트랩이라 불리는 방법을 통해 구 채우기의 밀도와 마법의 함수를 이해하는 새로운 접근법을 제시하기도 하였다.[10]

\(E_8\)이나 리치 격자와 같은 수학에서의 예외적 구조들은 수학과 이론물리학의 여러 분야에 종종 기대하지 않은 방식으로 등장한다. 그래서 다양한 분야의 수학이 한 곳에서 만나는 새로운 접점을 제공하기도 한다. 리치 격자와 긴밀한 몬스터 군의 문샤인 현상^{monstrous moonshine}도 그러한 예라고 할 수 있다. 이에 대한 더 깊은 이해의 추구는 때로 새로운 수학의 발견으로 이어진다. 그래서 이들은 마치 미지의 세계로 들어가는 미스터리의 입구처럼 보이기도 한다. 비야조우스카의 업적은 수학에서 예외적인 구조들의 이러한 역할에 대한 놀라운 이야기를 이어가는 것이다.