5월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
5월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신
신동건님께 문화상품권을 전달드릴 예정입니다.
먼저 1번 대칭 게임 문제를 풀어 보자. 충명도 당신도 X-초콜릿과 F-초콜릿을 모두 쓸 수 있고, 자신의 차례에 초콜릿 하나를 선택해서 내려놓는 것이다.
대칭 게임 문제의 해답은, 바로 충명이 놓은 초콜릿과 정확히 같은 모양의 초콜릿을 와플의 “반대편”, 즉 좌표가 (+100, +100) 만큼 떨어진 곳에 그대로 평행이동해서 놓는 것이다.
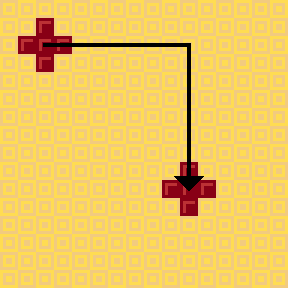
(200×200은 너무 크니까 16×16 와플로 표현했다.)
물론 좌표를 계산할 때는 와플의 상하좌우가 이어져 있다고 가정하고 계산하자. 문제에서 와플의 경계를 넘어가면 반대쪽에 놓는다고 했으므로 같은 와플이 무한히 상하좌우로 반복해 이어져 있다고 보아도 무방하기 때문이다. 충명이 어떤 지점에 초콜릿을 놓을 공간이 있었다는 말은 그 “반대편”에도 정확히 같은 모양의 초콜릿을 놓을 공간이 남아 있다는 말이므로, 당신은 언제나 초콜릿을 놓을 공간을 확보할 수 있다.
이제 2번 비대칭 게임 문제를 보자. 비대칭 게임 문제를 조금 변형하면 방금 푼 대칭 게임 문제와 같은 문제로 만들 수 있다. 와플을 이상한 안경을 끼고 본다고 생각해 보자.
이 안경은 와플과 그 위에 놓인 초콜릿을 왜곡해서 보여주며, 우리의 전략은 안경을 낀 채로 게임을 해서 대칭 게임을 하는 것이다. 즉, 충명이 보기에는 당연히 비대칭 게임으로 보이겠지만, 당신이 보기에는 대칭 게임처럼 보이게 하면 된다. 이제 우리가 할 일은 이상한 안경을 잘 디자인하는 것이다. 이상한 안경을 잘 디자인했다면 (와플이 왜곡되어 보이기 때문에) 충명이 언제나 X-초콜릿을 놓는 것처럼 보이지는 않겠지만, 대신 당신은 언제나 (+100, +100) 만큼 떨어진 곳에 충명이 놓은 초콜릿의 모양과 같은 모양의 초콜릿을 놓을 수 있게 될 것이다. 즉 이상한 안경을 쓴 당신의 시야 기준으로 충명이 F-초콜릿을 놓은 것처럼 보인다면 당신도 F-초콜릿을 와플의 “반대편”에 놓을 수 있어야 하고, 충명이 X-초콜릿을 놓은 것처럼 보인다면 당신도 X-초콜릿을 와플의 “반대편”에 놓을 수 있어야 한다. 이제 이 이상한 안경이 와플을 어떻게 왜곡해서 보여주어야 충명이 실제로 X-초콜릿을 놓았을 때 당신이 실제로는 F-초콜릿을 놓을 수 있는지를 찾기만 하면 된다.
당연히 실제로 X-초콜릿을 놓은 곳의 “반대편”에는 실제로 F-초콜릿이 와야 한다. 하지만 이상한 안경을 쓰고 보았을 때는 충명이 X-초콜릿을 놓았고 당신도 X-초콜릿을 놓았거나, 충명이 F-초콜릿을 놓았고 당신도 F-초콜릿을 놓은 것으로 보여야 한다. 다시 말해, 안경은 X-초콜릿이 놓인 위치에 따라 두 가지 중 하나의 기능을 수행해야 한다.
– 충명이 놓은 X-초콜릿은 왜곡하지 않고, 당신이 놓은 F-초콜릿을 왜곡해서 X-초콜릿처럼 보여준다.
– 충명이 놓은 X-초콜릿을 왜곡해서 F-초콜릿처럼 보여주고, 당신이 놓은 F-초콜릿은 왜곡하지 않는다.
가장 간단한 방법은 와플을 반으로 나누어서 한쪽은 “왜곡 영역”, 한쪽은 “일반 영역”으로 지정하는 것이다. 왜곡 영역 안에 X-초콜릿을 놓으면 F-초콜릿을 놓은 것처럼 보이고, F-초콜릿을 놓으면 X-초콜릿을 놓은 것처럼 보인다고 하자. 그러면 와플의 한 지점과 “반대편” 지점 중 하나는 항상 “왜곡 영역”에, 하나는 항상 “일반 영역”에 놓이므로, 충명이 놓은 X-초콜릿과 당신이 놓은 F-초콜릿 중 정확히 하나만 왜곡될 것이다.

(위쪽 절반은 왜곡 영역, 아래쪽 절반은 일반 영역이다.)
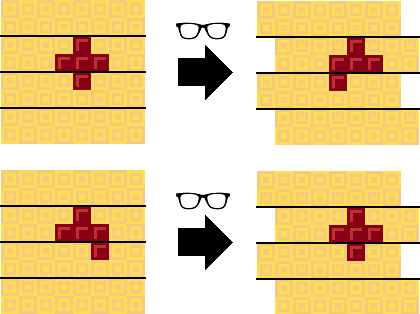
그러면 와플을 어떻게 왜곡해야 F-초콜릿을 X-초콜릿처럼 보이게, 그리고 X-초콜릿을 F-초콜릿처럼 보이게 할 수 있을까? 여기에서 중요한 관찰을 할 수 있는데, 바로 X-초콜릿을 살짝만 수정하면 F-초콜릿이 된다는 사실이다. X-초콜릿을 두 줄과 한 줄로 나눈 후 한 칸 밀면 반드시 F-초콜릿이 된다. 만약 와플에 두 줄마다 선을 긋는다면, X-초콜릿은 정확히 하나의 줄에 걸치게 될 것이다. 그렇다면 다음과 같은 왜곡을 생각할 수 있다.
보다시피 이런 왜곡을 사용한다면 X-초콜릿은 항상 F-초콜릿처럼 보이게 되고, F-초콜릿은 항상 X-초콜릿처럼 보이게 된다. 물론 F-초콜릿을 놓을 때는 위 그림과 같이 왜곡의 방향을 고려하여 알맞게 놓지 않으면 X-초콜릿처럼 보이지 않겠지만, F-초콜릿은 당신이 놓는 것이기 때문에 별로 문제는 되지 않는다. 당신이 알맞게 잘 놓으면 되니까.
이제 거의 다 왔다. “왜곡 영역”에만 위와 같은 왜곡이 적용되도록 하면 끝이다. 답안은 다음과 같이 정리가 가능하다.
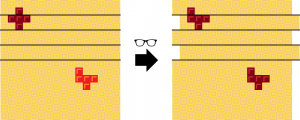
1. 다음과 같이 와플을 왜곡해서 보여주는 이상한 안경을 쓴다. 이상한 안경은 와플의 위쪽 절반의 칸들을 매 두 줄마다 한 칸씩 엇나가게 왜곡되어 보이게 한다.
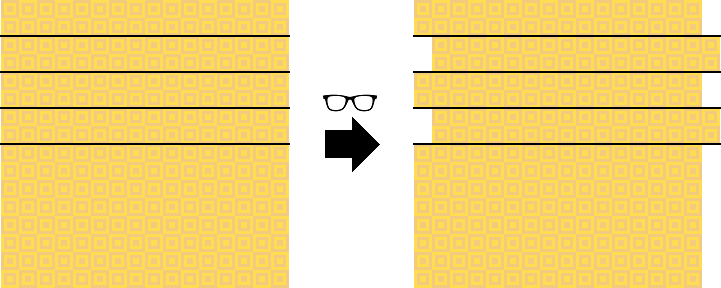
(왼쪽은 충명의 시야, 오른쪽은 이상한 안경을 쓴 당신의 시야에 보이는 와플의 모습이다.)
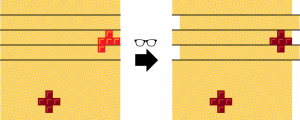
2. 왜곡된 와플을 보고, 충명이 놓은 초콜릿의 위치에서 (+100, +100)만큼 떨어진 곳에 충명이 놓은 초콜릿과 같은 초콜릿을 놓는다. 좌표가 와플을 벗어날 경우 와플의 상하좌우가 이어져 있다고 가정하고 계산한다.
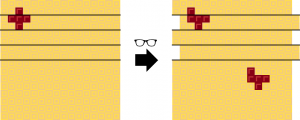
(충명이 놓은 초콜릿이 선에 걸친다면, 당신이 놓는 초콜릿은 선에 걸치지 않는다.)
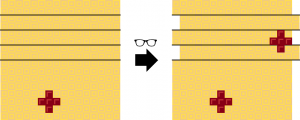
(충명이 놓은 초콜릿이 선에 걸치지 않는다면, 당신이 놓는 초콜릿은 선에 걸친다.)
3. 이 행동을 이상한 안경을 벗고 관찰하면, 당신은 항상 F-초콜릿을 놓고 있을 것이다.
(충명이 보기에, 당신은 항상 F-초콜릿을 놓고 있다.)
덤1. 이 전략에는 약간의 사소한 변형이 있을 수 있다. 가령 (+100, +100) 대신 (+0, +100)을 와플의 “반대편”으로 정의해도 된다. 또한 선으로 나뉜 매 영역을 [+0, +1, +0, …, +1, +0, +1] 만큼 왜곡하는 대신 [+0, +1, +2, …, +3, +2, +1] 만큼 왜곡해도 된다. 이외에도 몇 가지 사소한 변형이 가능하지만, 큰 틀은 같다.
덤2. 이 전략은 정사각형 와플의 한 변의 길이가 8의 배수일 때만 가능하다. 다행히도 와플의 크기는 200×200이므로 문제가 없다.
다음은 5월의 정답자로 선정된 신동건님의 해설입니다.
1. 따라서 대칭 게임의 경우, 상대방이 왼쪽 100칸에 초콜릿을 올려놓았을 경우에는 그 초콜릿의 오른쪽 100칸 위치에 동일한 초콜릿을 놓는 것이다. 오른쪽 100칸의 경우에는 왼쪽 100칸에 동일한 초콜릿을 놓는 것이다.
2. 하지만 비대칭 게임의 경우에는 동일한 초콜릿을 놓을 수 없지만, 힌트를 보면 X-초콜릿의 단 한 칸을 옆으로 밀면 F-초콜릿이 되니, 어떻게 X-초콜릿을 놓아도 항상 한 조각만이 다른 구역에 있도록 와플을 잘 나누어야 한다. 이는 와플을 두 줄 씩 번갈아 선택하여(그림의 노란색 구역과 초록색 구역) 선택된 구역에 있는 X-초콜릿을 한 칸 위나 아래로 미는 것이다. 이 때 위나 아래로 미는 규칙은 노란색 구역이 오른쪽 100칸 거리에 있는 초록색 구역의 한 칸 위가 되게 미는 것이다.
다시 말하면 왼쪽 100칸 X-초콜릿은 오른쪽 100칸 위치에 F-초콜릿을 노란색 영역의 X-초콜릿 조각이 한 칸 아래로 밀린 형태로 놓고, 오른쪽 100칸 X-초콜릿은 왼쪽 100칸 위치에 F-초콜릿을 초록색 영역의 X-초콜릿 조각이 한 칸 위로 밀린 형태로 놓는 것이다. 참고로 이 노란색 영역과 초록색 영역은 100칸 떨어진 영역과 다른 색이기만 하면 되며 그림에선 가로로 100칸만을 이동시켰으나 추가로 100칸을 이동시켜도 성립할 수 있다. 또한 영역을 가로로 이동시킬 수 있으며, 가로가 아닌 세로로 영역을 설정할 수도 있다.
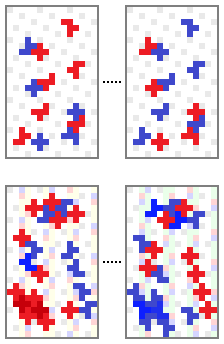
이를 종합하면 이러한 필승 전략은 2⁵⁰×2×4×2가지가 존재한다. 추가로 첫 번째 그림에서 회색 사각형은 X-초콜릿을 어떻게 놓아도 한 칸만을 차지하나 F-초콜릿은 그렇지 않은 것을 확인할 수 있다. 반면 두 번째 그림에서 X-초콜릿이 회색과 분홍색 사각형 중 단 하나의 칸만 차지함에 따라 F-초콜릿이 회색과 밝은 파란색 사각형 중 단 하나의 칸 만을 차지하는 것을 알 수 있다.