매월 정답자 한 분을 선정하여 고등과학원에서 문화상품권을 드립니다.
퍼즐 참여는 8월 28일까지 가능하며 9월 초 해설과 함께 정답자가 공개됩니다.
(답안과 함께 이름, 이메일과 전화번호를 포함한 연락처를 남겨주셔야 정답자 선정 연락이 가능합니다!)
다음과 같은 유명한 문제를 본 경험이 있는 독자들이 많을 것이다.
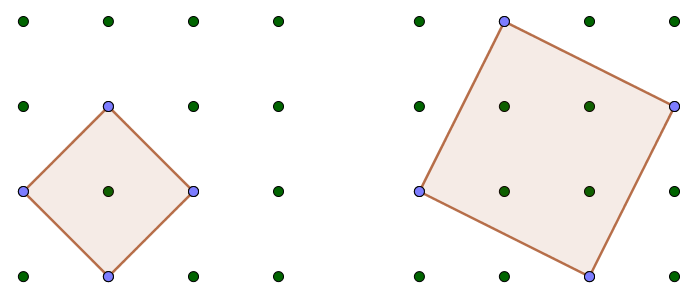
위와 같이 4 × 4 모양의 정사각 격자점들이 있다. 이 점들 중 일부를 꼭짓점으로 하여 만들 수 있는 정사각형은 총 몇 개일까?
한 변의 길이가 1인 것 9개, 2인 것 4개, 3인 것 1개로 하여 총 14개라고 답을 내는 사람이 많다. 하지만 이 문제에는 함정이 숨어 있는데, 이렇게 비스듬히 숨어 있는 정사각형까지 고려해야 한다는 것이다.
왼쪽과 같은 정사각형이 총 4개, 오른쪽과 같은 정사각형이 (좌우대칭을 감안하여) 2개가 있으므로 정답은 이를 합한 20개이다.
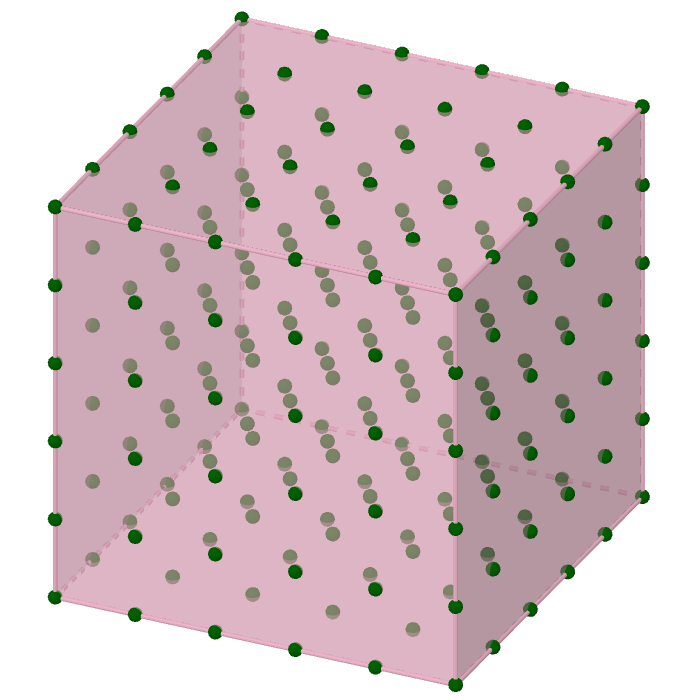
이번 달의 퍼즐은 이 문제를 3차원으로 확장한 것이다! 공간상에 다음과 같은 6 × 6 × 6 모양의 정육면체 격자를 생각하자.
좌표공간에서 x좌표, y좌표, z좌표가 전부 0,1,2,3,4,5 중 하나인 점들로 생각하면 된다. 이제 여기 있는 점들 중 일부만을 꼭짓점 삼아서 비스듬히 숨어 있는 정육면체를 하나 찾아 보자. 비스듬히 숨어있다는 것을 정확히 말하자면, 모서리들 중에 x축이나 y축, 혹은 z축에 평행한 것이 없다는 뜻이다.
힌트: 대칭을 고려하면 여러 가지의 답이 있지만, 그 중 하나는 (1,1,1)을 한 꼭짓점으로 갖는다.
이하는 좌표공간에서의 기하가 익숙하지 않은 독자들을 위한 팁이다.
좌표공간 위의 점들 A(a1,a2,a3),B(b1,b2,b3),C(c1,c2,c3),D(d1,d2,d3)에 대하여
- 선분 AB의 길이는
로 구한다.
- 선분 AB와 선분 CD가 수직인지 아닌지 알고 싶을 때는
의 값을 계산하여 0인지 아닌지를 살펴보면 된다. 0이 나오면 두 선분은 수직
이고, 0이 아니면 수직이 아니다.

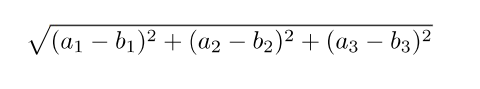
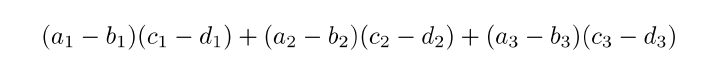


5 댓글
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.
Horizon 퍼즐에 답안이 제출되었습니다.