10월의 퍼즐에 참여해주신 모든 분들께 감사드리며,
참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신
박강민님께 문화상품권을 전달드릴 예정입니다.
세 조각인 상태에서 분리되지 않으려면, 그 중 두 조각이 하나로 합쳐져 있다고 생각했을 때에도 분리되지 않아야 한다. 그러므로 먼저 두 조각으로 나누어 본 다음, 그 중 하나를 다시 두 조각으로 나누는 전략을 생각해 보자.
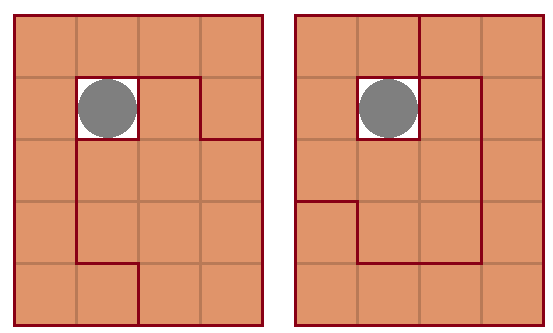
4방향 어디로 당겨도 빠지지 않도록 전체를 감싸는 조각을 만들어 보자. 전체를 감싸는 조각은 여러 방법으로 만들 수 있다. 예를 들면 다음과 같은 조각도 생각할 수 있다.
이제 안쪽에 있는 조각을 둘로 나누어서 답을 구성하는 것이 전략이다.
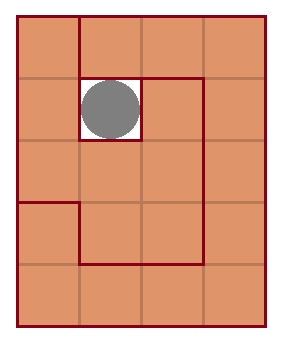
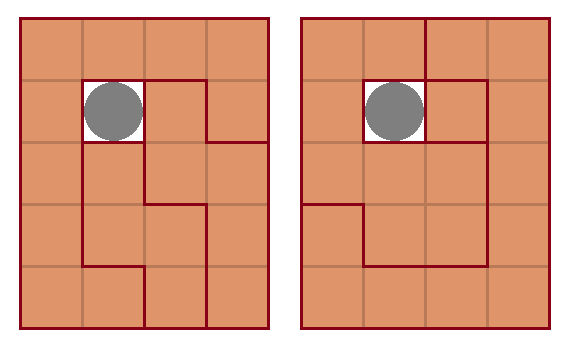
조각의 최소 크기가 있기 때문에, 전체를 감싸는 조각을 가능하면 작게 만드는 것이 좋을 것이다. 전체를 감싸는 조각의 최소 크기는 10칸이며, 동전을 빼냈을 때 분리될 수 있게 하려면 다음과 같이 두 가지 방법이 있다.
감싸진 조각을 둘로 나누어 보면 오른쪽 그림에서 다음과 같은 답을 얻는다.
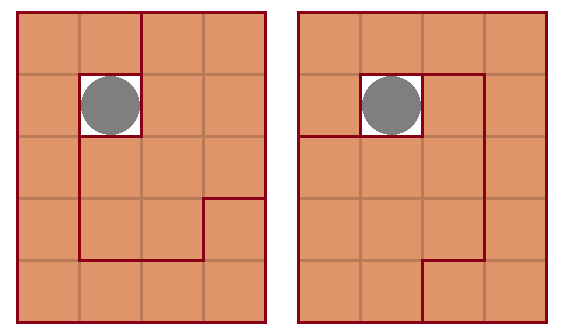
만약 전체를 감싸는 조각을 다른 방법으로 만들 경우, 2조각만으로는 동전을 빼내도 분리되지 않는 것을 확인할 수 있다.
이 상태에서 조각을 나누면, 동전을 빼내도 분리되지 않거나 조각의 최소 크기를 만족하지 못해 오답이 된다.
다음은 10월의 정답자로 선정된 박강민님의 해설입니다.
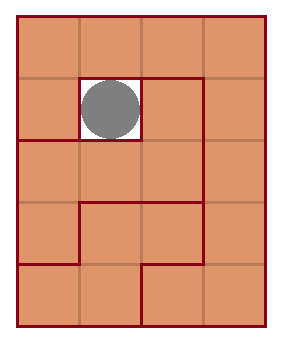
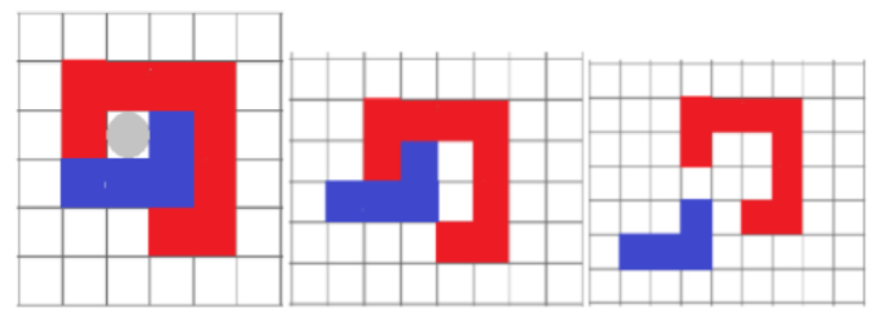
세 나무 조각들이 얽혀서 꼼짝없이 맞물려 있다 함은, 그 어느 세 조각중 아무 조각이나 골라 상하좌우의 방향으로 움직였을 때, 임의의 나무조각에 걸려 움직일 수 없다는 것을 의미한다. 이 때, 동전의 유무가 맞물림의 유무를 결정하니, 동전을 빼었을 때 슬라이딩 퍼즐처럼 나무조각들이 움직일 수 있는 틈이 생겨 빠져 나올 수 있어야 한다. 이 점을 잘 생각하면, 동전을 둘러싼 조각들 중 다음과 같은 메커니즘 활용한 ‘틀’을 찾을 수 있다. 핵심 조각으로는 전체적인 조각 뭉치를 붙들고 있는 조각 (빨간색), 동전이 빠져나가며 생긴 공간으로 상하좌우 평행이동하며 빠져나가는 조각 (파란색)이 있다.
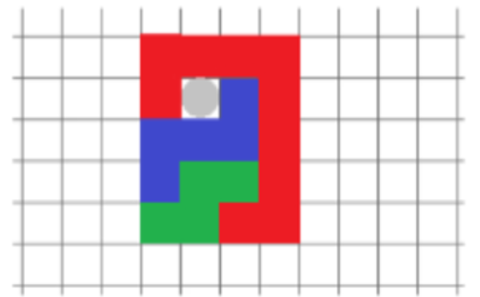
방금 보여준 ‘틀’은 좁은 공간에서 최소한의 조각과 공간을 사용해 만든 메커니즘의 예시이다. 자명하게 더 큰 공간인 4×5 격자에서는 남은 공간을 채워나가면서 위의 ‘틀’을 맞춘 경우는 여러가지가 있다. 하지만, 나무 조각이 단 3조각이어야 한다는 조건, 동전을 빼기 전에는 모두 서로를 붙들고 있어야 한다는 조건, 각 나무판의 최소 넓이는 4인 조건을 감안하면, 정답은 다음과 같다. 위의 ‘틀’에서 파란색 조각의 역할을 해치지 않고 서로 얽혀 고정되어 있는 넓이가 4인 초록색 조각이 추가된 모습이다.