[11월의 퍼즐해설] 해파리 가족의 힐베르트 호텔 바캉스

이 문제는 필자가 과거에 연구했던 모형론^{Model Theory}에서 수형 성질^{Tree Property}와 반사슬 수형 성질^{Antichain Tree Property}을 골라 처음 본 사람도 이해할 수 있게 변형, 각색한 것이다. 자세한 사항이 궁금한 독자는 논문(https://arxiv.org/abs/2106.03779)의 서장과 마지막 장의 예시 4.31을 참고하기를 바란다.

본문제

족보상의 모든 해파리들에게 서로 다른 소수^{Prime number}를 부여하자. 소수의 개수는 무한하므로 문제없이 지정할 수 있다.

다 지정했으면, 각 해파리가 머물 객실 번호를 ‘자신과 자신의 모든 후손 해파리들에게 부여된 각 소수들의 곱‘으로 계산한다. 직계의 경우 후손 집합이 포함관계에 있기 때문에 한 쪽이 다른 쪽의 배수가 되고(따라서 두 숫자 중에 작은 숫자가 공약수가 된다.) 방계의 경우 두 해파리의 후손집합은 서로소 관계에 있기 때문에(즉, 교집합이 공집합이기 때문에) 공약수가 될 수 있는 소수가 존재하지 않는다. 따라서 객실 번호는 서로소 관계가 된다.

보너스 문제

보너스 문제의 정답은 ‘가능하다’이다. 본 문제와 마찬가지로 소수를 어떻게 배정하느냐가 핵심이다.

해파리 가족의 모든 방계관계 쌍을 구하고, 이들 쌍에게 서로 다른 소수를 부여하자. 해파리 가족이 N명일 때 관계 쌍의 크기는 N(N-1)/2를 넘지 않으므로 유한하다.

다 지정했으면, 각 해파리가 머물 객실 번호를 ‘자신이 포함된 모든 방계관계 쌍마다 부여된 각 소수들의 곱’으로 계산한다. 두 해파리가 방계관계라면 그들 쌍에게 부여된 소수가 객실 번호의 공약수 역할을 한다. 역으로 두 해라피의 객실 번호 사이에 2 이상의 공약수가 있다면 둘은 방계관계이다. 이유는 다음과 같다.

공약수가 있다고 가정하고 가장 작은 소수 공약수를 p라고 하자. 객실 번호의 곱을 이루는 소수들은 방계관계 쌍마다 부여된 소수들이므로 p 역시 어떤 방계관계 쌍 {X, Y}에 부여된 소수였을 것이다. 그러면 객실 번호 정의에 의해 두 해파리는 모두 쌍 {X, Y}의 원소가 된다. 따라서 두 해파리는 방계관계이다. 대우를 취하면 직계관계의 해파리끼리는 객실 번호가 서로소임을 알 수 있다.

힐베르트 호텔은 자연수의 크기 만큼 방이 있는 가상의 호텔로 여러 퍼즐이 존재한다. 가장 먼저 모든 방이 차있는 호텔에 한 명이 또 오게 될 경우 n번 객실에 있는 손님은 n+1번으로 옮기면 1번 객실이 비게 된다. 마찬가지로 k명의 손님이 올 경우 n+k번으로 옮기면 k개의 객실이 비게 된다.

하지만 만약 다른 힐베르트 호텔이 문을 닫아 자연수의 크기 만큼의 또다른 손님이 온다면 무한히 멀리 있는 방으로 옮길 수는 없으니 다른 방법을 생각해야 한다. 그 방법이란 바로 2×n번 객실로 옮기는 것으로 그러면 홀수 번 객실은 남게 되어 무한히 많은 손님을 받을 수 있다. 마찬가지로 k개의 힐베르트 호텔에서 손님이 온다고 해도 k×n번 방으로 옮기고 각각 k×n+1번 방, k×n+2번 방…에 손님을 받을 수 있다.

만약 무한한 힐베르트 호텔에서 우리 힐베르트 호텔로 오게 된다면 어떻게 해야할까? 이번에는 번호를 붙이는 방법을 달리해야만 한다. 그 방법이란 우리 호텔부터 호텔의 번호를 1번부터 매겨서 i번 호텔의 j번 객실에 있었던 손님은 i번째 소수인 p_i^j번 객실로 옮기면 된다. 이것이 가능한 이유는 소수가 무한하며 합성수 또한 무한하기 때문이다. 따라서 우리 호텔의 1번 객실에 있던 손님은 2번 객실로, p_1=2번 호텔의 2번 객실의 손님은 (p_2=3)^2=9번 객실로, 9번 호텔의 3번 객실은 (p_9=23)^3=12167번과 같이 옮기면 모든 손님을 수용하고도 무한한 빈 객실도 생겼다. 빈 객실이 싫으면 우리 호텔을 제외하고 나머지를 이렇게 부여하고 나머지는 남은 객실을 순차적으로 부여할 수도 있고, 또는 i번 호텔의 j번 객실 손님을 (i,j)번이라 두고 (1,1),(2,1),(1,2),(3,1),(2,2),… 순서대로 수용해도 된다.

그러나 문제에서 컨시어지가 물어본 무한 수열을 번호로 갖는 무한한 손님이 있다면 어떻게 될까? 이 경우에는 모든 손님을 힐베르트 호텔에 수용할 수 없다. 그것도 무한히 많은 손님을 돌려보내야 할 것이다. 어떻게든 무한한 손님을 객실에 배정했다고 가정하자, 그러면 객실에 수용된 사람들의 번호 리스트를 보게되면 빠진 사람이 존재하는 것을 확연히 볼 수 있다. 바로 1번 객실의 첫번째 번호에 1을 더한 값이 첫번째 번호이고 2번 객실의 두 번째 번호에 1을 더한 값을 두 번째 번호로 갖고 … 이런 번호를 가진 손님은 리스트의 모든 번호와 맞지 않으니 아직도 프런트에서 항의하고 있을 것이다. 이 손님 뿐만 아니라 객실의 순서를 바꾸어서 구한 번호의 손님, 1이 아닌 수를 더한 번호의 손님들로 무한한 손님이 프런트에서 항의하고 있으니 빨리 호텔을 닫고 도망가는게 좋을 것 같다.

어째서 이런 일이 일어났을까? 무한한 힐베르트 호텔에서 온 손님을 수용할 수 있었는데 같은 방법으로 i번째 번호가 a_i인 손님을 ∏p_i^a_i번 객실로 배정하면 되는게 아닐까?라는 생각으로 바로 앞에서 기다리는 손님의 번호가 {5,1,2,0,0,0,…}이라고 하면 2^3×3^1×5^2×7^0×…=360000번으로 배정하면 되겠다고 생각한 찰나, 두 번째 손님의 번호는 약간 익숙한 {3,1,4,1,5,9,…}번이다. 분명히 같은 방법으로 배정하려는데 이 번호는 무한히 있어 무한한 소수를 곱해야 하므로 무한은 수가 아니기 때문에 객실을 지정할 수 없다.

서론이 길었지만 여기서 손님은 딱히 어떤 방을 달라고 하진 않는 고분고분한 손님들이였지만 이 해파리 가족들은 조건이 붙은 까다로운 손님들이다! 똑같은 방법은 쓸 수 없지만 적어도 소수는 무한하다는 사실만은 쓸만해 보인다.

해파리 가족들이 부탁한 조건은 직계는 서로소가 아니여야 하고 방계는 서로소여야 한다는 조건이니 가장 간단하게 직계와 방계가 있는 상황을 보면 1번과 1-1번, 1-2번만 있다고 생각하자. 이 경우 1-1번은 2번 객실, 1-2번은 3번 객실, 1번은 6번 객실로 배정을 하면 해결이 된다. 이 방법을 일반화 하기 위해 분석해보자면 서로소인 자녀들의 객실 번호의 곱이 선조의 객실 번호가 된다. 이 방법에는 결함이 있는데 바로 자녀가 한 명일 경우에는 동일한 방에 배정된다는 것이다. 이 문제 또한 해결하기 위해서는 자녀의 객실 번호를 제곱하면 다른 방에 배정되면서도 다른 소인수를 갖지 않는다. 따라서 문제를 해결하는 방법은 다음과 같다.

1. 자녀가 없는 해파리들에게 우선적으로 소수 번호 객실을 부여한다.
2. 번호가 부여된 해파리들의 조상의 번호를 자녀들의 번호의 곱으로 객실을 부여한다.
2-1. 자녀가 한 명일 경우에는 번호를 제곱한다. 이를 실제 예시에 적용하면 해파리들의 번호가 각각 1, 1-1, 1-1-1, 1-2, 1-2-1, 1-2-1-1, 1-2-2, 1-3이라면 배정되는 객실의 번호는 각각 1260, 4, 2, 45, 9, 3, 5, 7번이 된다. 문제는 해결되었지만 다른 자손들은 최대 45번 객실에 있는데 최초의 조상은 1260번이나 되는건 너무 멀다고 느껴진다. 그러면 조금 더 작은 수로 배정해보려면 다음과 같다.
2. 번호가 부여된 해파리들의 조상의 번호를 모든 자녀들의 객실 번호의 소인수를 곱으로 객실을 부여한다.
2-1. 자녀가 한 명일 경우에는 자녀의 번호에 가장 작은 소인수를 곱한 값을 부여한다.
아까와 동일한 1, 1-1, 1-1-1, 1-2, 1-2-1, 1-2-1-1, 1-2-2, 1-3번 해파리는 이 방법을 이용하면 각각 210, 4, 2, 15, 9, 3, 5, 7번 객실이 부여된다.

이번엔 반대로 직계는 서로소, 방계는 2이상 공약수의 조건을 보자. 최소 조건인 1, 1-1, 1-2번은 각각 1, 2, 4번 객실로 배정된다. 일반화를 하려 해도 직계와 달리 방계는 비직관적이기 때문에 어려움이 있지만 무조건 방계로만 이루어진 그룹을 찾을 수 있으며 같은 대(代)를 모으면 무조건 방계다. 이전 문제에서도 계속 직계 조상으로 모으면 반드시 모두 직계로 이루어지기 때문에 같은 공약수를 두어도 되었으므로 같은 대가 같은 공약수를 공유하게 만들면 된다. 또한 최초 조상인 1은 모든 자손과 직계 관계이므로 1으로 두면 된다. 가장 먼저 생각난 방법은 각각의 해파리에게 하나의 소수를 부여하고 직계가 아닌 모든 해파리가 그 값을 곱하면 될것 같지만 다른 직계가 서로소가 아니게 된다. 같은 서로소를 가져도 괜찮은것은 모두 방계로만 이뤄진 집합, 즉, 대를 살짝 변형하면 된다. 각 해파리는 하나의 수를 부여 받는게 아닌 대의 수 만큼 부여받는다. 그 다음 각각의 대에 대응하는 부여된 수를 곱하되 직계를 제외한다. 이때 최초의 조상은 항상 직계이므로 제외하고 자신의 대는 변형이 가해지지 않으므로 동일한 수를 사용한다. 이때 위의 대에 대응하는 수를 부여하면 두 번 부여된 수가 곱해지므로 아랫 대에 대해서만 부여한다. 이 방법에서 중복은 마지막 대에 형제가 존재할 경우 발생하며 이전 문제에서 해결한 방법처럼 가장 작은 소인수를 곱해주면 된다. 이에 따라 문제를 해결하는 방법은 다음과 같다.

1. 1번 해파리는 1번 객실에 배정한다.
2. 1대를 제외한 모든 대에 소수를 부여한다.
3. 모든 해파리에게 자신의 아랫 대에 대한 수를 각각 부여한다.
4. 자신의 대에 부여된 수와 직계가 아닌 모든 윗 대에 부여된 자신의 대애 해당하는 수를 곱한다.
5. 마지막 대의 경우 형제자매가 존재할 시 순차적으로 가장 작은 소인수를 거듭제곱하여 곱한다.

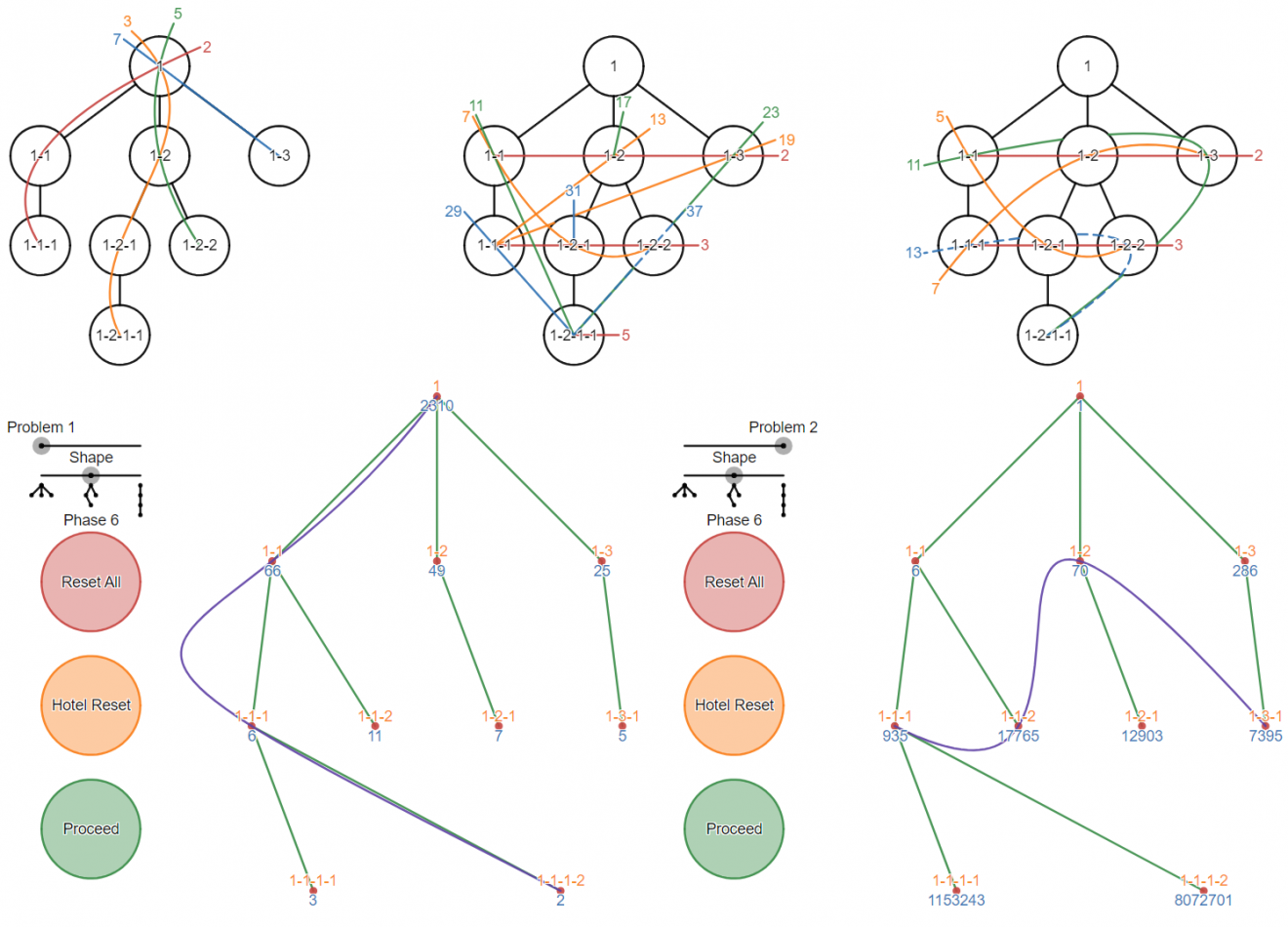
이 방법으로 이전 문제에도 사용된 1, 1-1, 1-1-1, 1-2, 1-2-1, 1-2-1-1, 1-2-2, 1-3번 해파리의 번호를 부여하면 1, 154, 21489, 442, 12369, 1357345, 14763, 874번이 배정된다. 1357345는 커도 너무 크기 때문에 조금 더 최적화를 하고 싶지만 이는 모든 경우에 대해서 일반화하기는 어려우나 쓸 수 있는 방법으로는 위의 경우에서 5나 17, 31의 경우에는 단 하나의 번호만 소인수로 가지니 이 경우에 대해서는 고려하지 않아도 된다. 하지만 이 경우 생기는 문제는 최초의 선조부터 하나의 자손만 내려올 경우 전부 1이 배정되므로 예외적으로 소수를 곱해주어야 한다. 이에 따른 결과는 1, 70, 8151, 22, 195, 52003, 4485, 442가 된다. 또한 예시에 특화시킨 경우는 1, 110, 273, 14, 15, 143, 195, 770이 된다. 이를 다시 보니 최소로 필요한 소수의 개수는 자손이 없는 두 해파리 중 공통 조상까지 각자 직계의 수를 곱한 값의 최대이다. 우리의 예시에서는 1-1-1과 1-2-1-1의 공통 조상인 1까지 각각 2명과 3명의 조상이 있으니 최소 6개의 소수가 필요하다.

이와 같은 문제와 풀이에서 dobble이라는 보드게임이 연상된다. dobble은 모든 카드에 여러 문양이 있지만 어떤 두 카드를 선택해서 단 하나의 동일한 문양을 찾는 게임으로 항상 유일하게 존재한다. 만약 직계와 방계가 아닌 임의의 조합에서만 공통된 문양이 있게 만드려면 각각 공약수가 존재해야하는 관계에 대해 소수를 부여하고 그 관계에 해당하는 해파리에게만 그 소수를 곱해주면 다른 모든 관계에는 그 소수가 존재하지 않으니 서로소가 된다. 이 경우 관계의 수 만큼 소수가 필요하므로 n명이 존재하면 최대 n(n-1)개의 소수가 필요하며, n(n-1)번째 소수는 대략 n(n-1)log(n(n-1))≒2n²logn이며 각 해파리에게 n개의 관계가 있으니 최대로 가능한 수는 대략 2n^(2n+1)logn이다. 또한 모든 관계에 공약수가 있는 집합을 찾을 수 있다면 그들의 관계를 단 하나의 소수로 묶어줄 수 있다.

위에서 설명한 경우는 아래 링크에서 임의의 크기로 모두 확인할 수 있다.
https://www.desmos.com/calculator/iihgggnbtb