[12월의 퍼즐해설] 고장난 TV와 거짓말쟁이 퀴즈쇼

우리는 참말쟁이 3명만 찾아내면 된다. 그러면 나머지 3명이 거짓말쟁이다.

충명은 모자 6개 중 5개를 보고 있으므로 당연히 자기 모자의 색을 알 것이다. 실제로 자기 모자의 색을 알겠다고 했으니 충명은 반드시 참말쟁이다.

한편, 초록 모자와 빨간 모자를 대화만으로 구분할 방법은 없으므로, 아무 모자도 보지 못하는 진후는 절대로 자기 모자의 색을 알 수 없다. 실제로 자기 모자의 색을 모르겠다고 했으니 진후도 반드시 참말쟁이다. 이제 나머지 한 명의 참말쟁이만 찾으면 된다! 충명 다음 차례인 현모부터 다시 보자.

현모는 모자 4개를 보고는 모르겠다고 했다. 현모가 본 4개의 모자 중 같은 색의 모자 3개가 있으면 (□□□■) 현모는 자기 모자의 색을 알 것이다. 반면 모자를 색깔별로 2개씩 보고 있다면 (□□■■) 대칭에 의해 자기 모자의 색은 절대 알 수 없다. 현모는 자기 모자의 색을 모르겠다고 했으므로 두 가지 가능성이 있다. 현모가 □□□■를 보았고 거짓말쟁이거나, 현모가 □□■■를 보았고 참말쟁이거나.

창현은 모자 3개를 보고는 알겠다고 했다. 창현이 본 모자들의 색이 모두 같으면 (□□□) 당연히 창현은 자기 모자의 색을 알 것이다. 반면 앞의 모자 3개의 색이 2개/1개로 나누어진다면 (□□■) 자기 모자의 색은 알 수 없다. 창현은 현모가 거짓말쟁이인지 참말쟁이인지 모르기 때문에 현모가 □□□■를 봤는지 □□■■를 봤는지도 알 수 없어 현모의 대답도 아무런 도움이 되지 않는다. 즉 창현은 자신이 본 모자만 보고 자신의 모자의 색을 추측해야 하는 상황이다. 창현은 자기 모자의 색을 알겠다고 했으므로 두 가지 가능성이 있다. 창현이 □□□를 보았고 참말쟁이거나, 창현이 □□■를 보았고 거짓말쟁이거나.

정휘는 자신의 모자를 모르겠다고 했다. 정휘가 같은 색의 모자 2개를 보고 있다면 (□□) [창현이 □□□를 보았고 참말쟁이 + 현모가 □□□■를 보았고 거짓말쟁이]였을 수도 있고 [창현이 □□■를 보았고 거짓말쟁이 + 현모는 아무거나]였을 수도 있다. 정휘가 지금까지의 대화로 정체를 추측할 수 있는 충명, 현모, 창현 그리고 자기 자신까지 포함해서 4명 전부가 참말쟁이거나 4명 전부가 거짓말쟁이일 경우가 있었다면 참말쟁이와 거짓말쟁이가 각각 3명이라는 제한조건을 통해 그런 경우의 수를 제거할 수 있었겠지만, 지금은 참말쟁이와 거짓말쟁이가 섞여 있는 것으로 추론되니 이 제한조건도 도움이 안 된다. 즉, 정휘가 □□를 보고 있다면 정휘는 자기 모자의 색을 알 수 없다. 한편, 정휘가 모자를 색깔별로 하나씩만 보고 있다면 (□■) 대칭에 의해 자기 모자의 색은 절대 알 수 없다. 따라서 어느 경우든 정휘는 절대 자기 모자의 색을 알 수 없었을 테고, 당신은 정휘가 참말쟁이임을 확신할 수 있다.

참말쟁이 3명을 다 찾았으므로 동규는 따져볼 필요도 없다. 충명, 정휘, 진후가 참말쟁이고, 따라서 거짓말쟁이는 현모, 창현, 동규다.

위의 풀이는 문제에 오류가 없다고 (즉, 해답이 존재한다고) 가정한 상태로 푼 것이다. 물론 (출제자를 신뢰한다면) 이는 합당한 가정이며 그렇게만 풀어도 충분히 좋은 답안이다. 하지만 만약 문제가 정말 오류가 없는지 직접 검증해 보고 싶다면 모든 경우의 수를 꼼꼼히 따져야 한다. 가령 동규도 참말쟁이라는 결론이 나온다면 문제가 잘못된 것이니까.

가장 먼저 충명이 알겠다고 한다. 충명이 보고 있는 모자의 색은 반드시 3개/2개로 나뉠 것이며 충명은 자신의 모자 색이 남은 하나라는 것을 안다. 따라서 충명은 반드시 참말쟁이다. 여기까지 가능한 모든 경우의 수를 표로 만들어 보자.
위 표는 현재까지의 대답을 이끌어낼 수 있는 모든 경우의 수를 나타낸다. 모든 참가자는 들리는 대답만 가지고 머릿속으로 이 표를 떠올릴 것이고, 자신의 모자 색을 추론할 때 이 표에 있는 모든 가능성과 자신이 실제로 보고 있는 모자의 색들을 비교하며 가능성을 점점 간추려 갈 것이다.

현모가 모른다고 한다. 즉, 현모가 자기 모자의 색을 안다면 거짓말쟁이, 모른다면 참말쟁이다. 현모가 보는 모자 4개의 색 조합의 가짓수를 모두 나열하고, 이 가짓수를 만들 수 있는 조합을 위의 표에서 뽑아서 새로운 표를 그리면 다음과 같다.위 표에서 “계승”이란, 앞선 표에 있던 가능성 중 어느 가능성에서 이 경우가 될 수 있는지를 보기 편하게 나타낸 것이다.

창현이 알겠다고 한다. 즉, 창현이 자기 모자의 색을 안다면 참말쟁이, 모른다면 거짓말쟁이다. 창현이 보는 모자 3개의 색 조합의 가짓수를 모두 나열하고, 이 가짓수를 만들 수 있는 조합을 위의 표에서 뽑아서 새로운 표를 그리면 다음과 같다.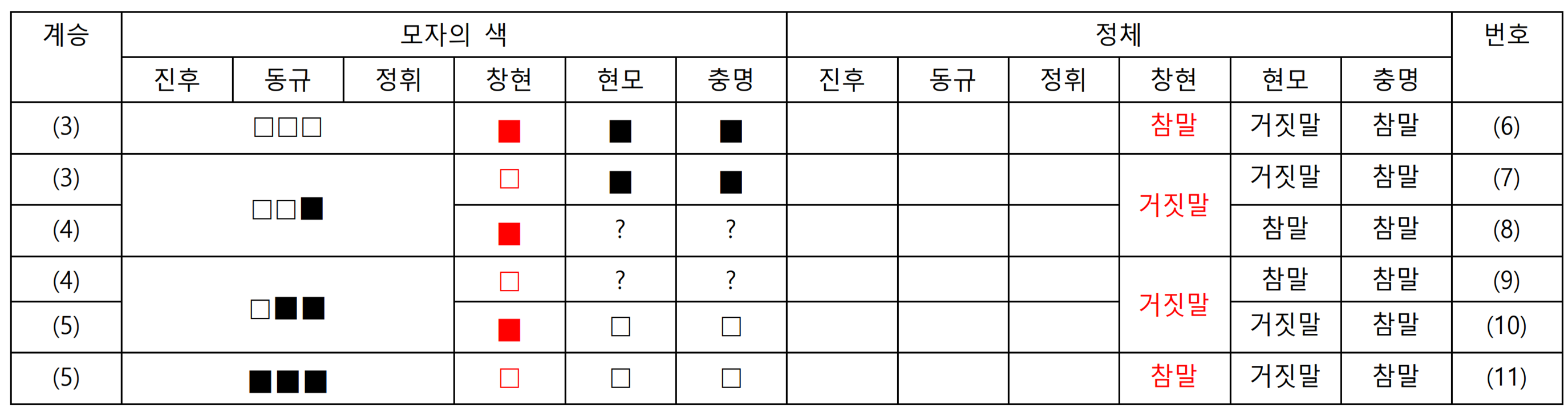정휘가 모른다고 한다. 즉, 정휘가 자기 모자의 색을 안다면 거짓말쟁이, 모른다면 참말쟁이다. 정휘가 보는 모자 2개의 색 조합의 가짓수를 모두 나열하고, 이 가짓수를 만들 수 있는 조합을 위의 표에서 뽑아서 새로운 표를 그리면 다음과 같다.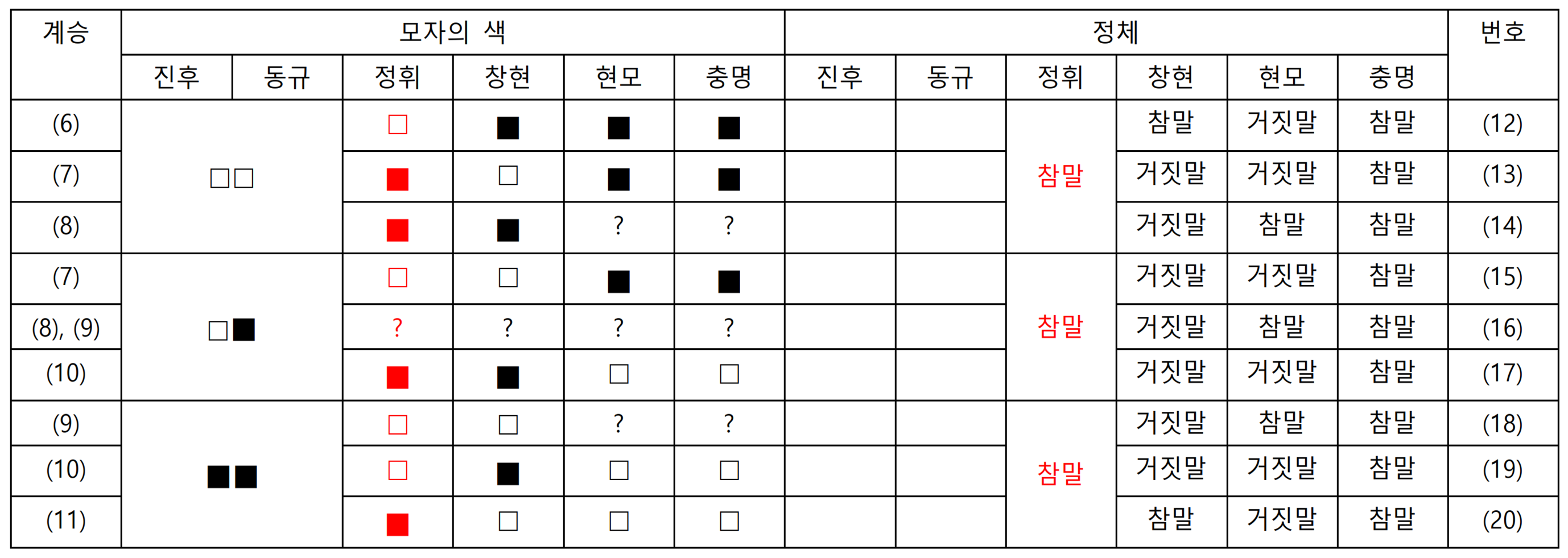동규가 알겠다고 한다. 즉, 동규가 자기 모자의 색을 안다면 참말쟁이, 모른다면 거짓말쟁이다. 동규가 보는 모자 색의 가짓수를 모두 나열하고, 이 가짓수를 만들 수 있는 조합을 위의 표에서 뽑아서 새로운 표를 그리면 다음과 같다.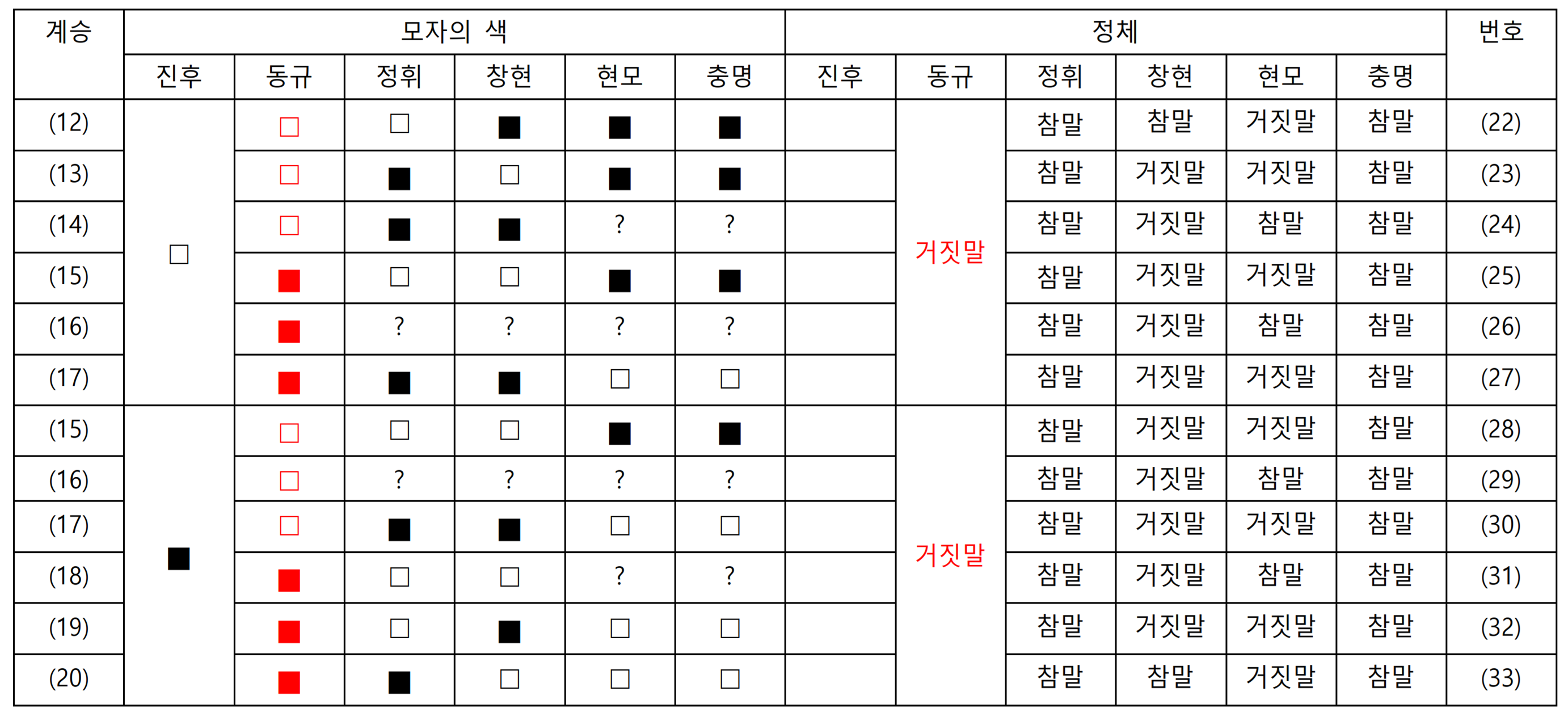진후는 볼 수 있는 모자가 없으므로 들은 정보만 가지고 판단해야 하는데, 모자 색 대칭에 의하여 진후는 자기 모자의 색을 절대 알 수 없고 따라서 반드시 참말쟁이다. 따라서 위의 표에서 거짓말쟁이가 3명, 참말쟁이가 2명 밝혀진 경우들만 모두 가져오면 된다.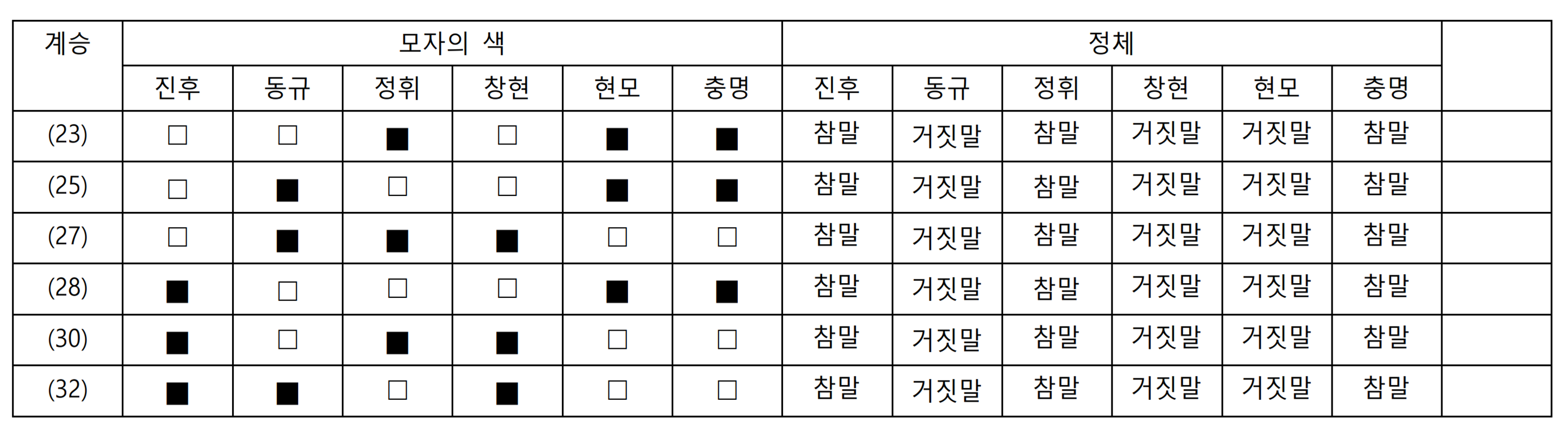이와 같은 대답이 나올 수 있는 조합은 구체적으로 6가지가 있으며, 이 중 어떤 경우든 거짓말쟁이는 동규, 창현, 현모라는 것을 확인할 수 있다.

정휘는 참말쟁이이다. 정휘가 거짓말쟁이일 경우 절대로 자기 차례에 모자색을 알 수 없음을 보이겠다. 정휘 앞에는 모자가 두개밖에 없으므로 정휘가 자기 모자 색을 아는 방법은 자기 모자를 빨강으로 가정했을 때 대답에 모순이 있거나 초록으로 가정했을 때 앞선 대답 중에 모순이 나오는 경우밖에 없다.

여기서 뒤에 셋이 참말쟁이인지 거짓말쟁이인지는 모르므로 ‘모순’이 나오려면 자신을 포함해 정휘 창현 현모 충명 네명 전부가 참말쟁이 이거나 거짓말쟁이여야 한다. 하지만 충명은 참말쟁이이므로 정휘가 거짓말쟁이라면 자신의 모자색을 어떻게 가정해도 모순이 생기지 않는다.

즉, 자신의 모자색을 알수없다. 거짓말쟁이라면 y라고 대답했을것이므로 정휘는 반드시 참말쟁이이다. 즉 진후 정휘 충명이 참말쟁이이다.
(창현 이상은 앞에 셋의 모자색으로 자신의 모자색을 맞출수도 있으므로 같은 논리를 적용할수 없고 동규이하도 뒷쪽 다수들중 모순이 나오는 경우가 다양해지므로 같은 논리가 적용안됨)