2023년 아벨상 수상자 루이스 카파렐리Luis Caffarelli는 비선형 편미분방정식의 자유 경계 문제비국소 방정식과 같은 새로운 분야들을 이끌고, 몽지-암페어 방정식 나비에-스톡스 방정식 등에 새로운 관점의 증명을 도입하는 천재적인 업적을 남겼습니다. 그는 수많은 수학자들과의 공동 연구로 400여편의 논문을 작성할 정도로 다양한 연구를 하였지만, 그의 초기 연구이자 대표 업적인 자유 경계 문제free boundary problem를 먼저 이야기할 수 밖에 없겠습니다.
자유 경계 문제
1948년 아르헨티나의 수도인 부에노스 아이레스에서 태어난 카파렐리는 선박의 기계 엔지니어로 해운업에 종사하던 아버지에게 영감을 받아 공학과 과학에 관심을 가지게 되었습니다. 그는 1967년 부에노스 아이레스 대학에 입학하여 물리학과 수학을 전공하였고, 동대학에서 1972년 박사 학위를 받았습니다. 이후 미국의 미네소타 대학에 연구원으로 합류하여 동대학의 조교수, 부교수, 교수로 진급하며 10여년을 미네소타에서 지냈습니다. 미네소타에서 비선형 편미분방정식과 최소 곡면을 연구하던 한스 레비Hans Lewy에게 자유 경계 문제의 일종인 장애물 문제를 소개받는 등 많은 영향을 받은 그는 1977년 고차원 자유 경계의 정칙성에 관한 논문을 발표하여 크게 주목 받았습니다.
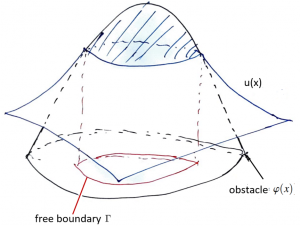
자유 경계란 식탁 위에 떨어진 물방울의 경계선, 번져 나아가는 산불의 경계선, 물 속에서 녹고 있는 얼음의 표면과 같은 것을을 일컫습니다. 예를 들어, 식탁 위의 물방울의 표면은 장력과 중력이 균형을 이루어 힘의 합력이 영이 되는 미분방정식(주석 : 이 방정식의 해들을 특별히 모세관 곡면capillary surface이라고 부릅니다.)을 만족합니다. 또한 이 물방울의 표면과 식탁과 특정한 각도를 이루며 만나는데, 이 각도는 마찰 계수에 따라 정해집니다. 문제는 물방울의 표면과 식탁이 만나는 경계선이 정해져 있지 않기 때문에, 우리는 이를 자유 경계라고 부릅니다. 다시 말해, 어떤 알 수 없는 자유 경계를 가지는 정의역 위에서 노이만Neumann 경계 조건(주석 : 정의역의 경계에서 미분방정식의 해의 법벡터 방향의 편미분값이 만족해야하는 조건)을 만족하며 정의되는 미분방정식의 해를 연구해야 한다는 뜻입니다.
Free boundary problem
일반적인 미분방정식은 정의역이 주어져있으며, 정의역이 좋은 성질을 가질 때 방정식의 해도 좋은 성질을 가진다는 것을 증명할 수 있습니다. 반대로 정의역이 매우 이상하다면, 방정식의 해가 좋은 성질을 가질 수 없을 뿐더러, 방정식에 따라 해가 존재하지 않을 수도 있습니다. 따라서 자유 경계 문제는 정의역에 대한 정보가 없으므로 기존의 미분방정식 이론으로는 다루기 매우 힘들었습니다. 선행 연구들의 경우 경계가 선인 2차원에서 주로 연구가 되고 있던 중에, 카파렐리는 고차원에서 에너지를 극소화하는 자유 경계 문제의 해는 두 번 미분 가능한 고전적인 해이며, 경계면 또한 미분가능하다는 것을 증명하였습니다.
자유 경계 문제의 해는 스칼라 함수scalar function이지만 해의 경계는 초곡면hypersurface입니다. 따라서 극소 곡면minimal surface과 같이 미분방정식을 만족하는 곡면을 연구하는 미분기하학과 깊은 관계가 있습니다. 실제로 카파렐리의 자유 경계 문제는 미분기하학의 정칙성 이론과 관계가 깊고, 50여년이 지난 지금도 미분방정식과 미분기하학의 주요 접점 중 하나로 연구되고 있습니다.
비국소 방정식
자유 경계 문제가 카파렐리의 초기 연구라면 그의 최근 연구는 비국소 방정식이라고 할 수 있겠습니다. 비국소 방정식이란 국소적으로 정의되지 않은 항이 있는 방정식을 의미합니다. 일단 우리가 처음 배우는 거의 모든 미분방정식은 국소적으로 정의됩니다. 예를 들어, 뉴턴의 제2법칙인 F=ma를 사용하여 파동 방정식을 유도해보겠습니다. 균일한 밀도를 가지는 고무줄의 운동을 생각하면 질량을 m=1로 고정할 수 있습니다. 그리고 각 시간t의 고무줄을 그래프 (x,u(x,t))라고 하면, 힘은 고무줄에 걸리는 장력으로 공간 방향의 이계도함수로 가정할 수 있습니다. 즉, F=u_{xx}. 그리고 가속도는 시간 방향의 이계 미분이므로 a=u_{tt}. 따라서, 고무줄의 운동은 파동방정식 u_{tt}=u_{xx}을 따릅니다. 이 방정식의 두 항 u_{xx}와 u_{tt}는 각 점에서 정의되므로 파동방정식은 비국소 방정식이 아닙니다. 그 외에도 라플라스 방정식, 열방정식 등 기본적인 방정식들은 모두 국소적으로 정의되고, 20세기까지 대부분의 연구는 국소적으로 정의되는 방정식에 집중되었습니다.
하지만 우리가 현실에서는 비국소 방정식으로 표현되는 현상들을 흔히 접할 수 있습니다. 예를 들어, 풍선은 비국소 방정식을 만족합니다. 평형 상태의 풍선은 내부를 향하는 표면 장력과 풍선 안밖의 기압차에 의한 압력이 평형을 이루어 정지해 있습니다. 이 때, 표면 장력은 풍선의 각 점의 평균 곡률로서 국소적으로 정의되는 국소 변수이지만, 압력은 줄어든 풍선의 부피에 의해 결정되는 것으로 적분을 통하여 구할 수 있는 대역global 변수입니다. 따라서, 풍선의 미분방정식은 비국소 방정식입니다. 이 외에도 금융 수학에서 확률적stochastic 제어를 위하여 사용하는 레비 과정 Levy process는 미분과 적분이 모두 들어가는 비국소 연산자입니다. 또한 유체를 기술하는 볼츠만 방정식Boltzmann equation이나 합계분산 방정식aggregation-diffusion equation 역시 비국소 방정식이며, 그 외에도 흔히 찾아볼 수 있습니다.
\( (-\Delta)^s u(x)=\frac{4^s\Gamma(\frac{n}{2}+s)}{\pi^{\frac{n}{2}}\Gamma(-s)}\displaystyle\lim_{r\to 0^+}\int_{\mathbb{R}^n\setminus B_r(x)}\frac{u(x)-u(y)}{|x-y|^{n+2s}}dy \)
Fractional Laplacian
이러한 비국소 방정식의 가장 기본이 되는 방정식은 분수 라플라시안fractional Laplacian 방정식이라고 할 수 있습니다. 카파렐리는 그의 제자 Silvestre와 2007년 공동 발표한 논문에서 분수 라플라시안 연산자가 제곱근 라플라시안 연산자와 마찬가지로 반평면의 조화 함수로의 확장 문제로 변환될 수 있다는 것을 보였습니다. 이는 비국소 문제를 국소 문제를 사용하여 다룰 수 있게 해주는 도구로서 현재까지 약 2900번 인용되어, 그의 논문 중 가장 많이 인용되었습니다. 비국소 문제는 21세기에 가장 활발하게 연구된 미분방정식의 분야 중 하나이지만, 아직까지도 매우 제한적인 상황에서만 이론을 전개할 수 있는 난해한 분야로, 카파렐리와 그의 동료들을 비롯한 많은 수학자들의 지속적인 관심을 받고 있습니다.
나비에-스톡스 방정식과 몽지-암페어 방정식
나비에-스톡스Navier–Stokes 방정식은 유체의 흐름을 기술하는 방정식으로 3차원에서 해가 특이점1을 가질 수 있는지 없는지 증명하는 것은 클레이 수학연구소에서 100만 달러의 현상금을 내건 7개의 수학 난제 중 하나도 현재까지 미해결 난제로 남아있습니다. 카파렐리는 콘Kohn, 니렌버그Nirenberg 2와 함께 나비에-스톡스 방정식의 해의 부분 정칙성에 대한 논문을 1982년에 발표했습니다. 이 논문에서 이들은 해의 특이 집합(주석:특이점들의 집합)은 시공간(주석: 포물형 미분방정식에서는 시간 방향 일계도함수가 공간 방향 이계도함수에 대응되어야하기 때문에, 시간 차원을 2차원으로 봅니다. 따라서 n차원 나비에-스톡스 방정식의 해가 정의되는 시공간 집합은 n+2차원으로 생각합니다.)에서 하우스도르프Hausdorff 차원이 5/3이하이며, 각각의 고정된 시간에서 특이 집합의 하우스도르프 차원은 1이하라는 것을 증명하였습니다. 이는 곧 방정식의 해가 특이점을 가진다 하여도 특이 집합은 매우 작다는 것을 의미합니다.
\( \vec{u}_t=\Delta \vec{u}-(\vec{u}\cdot \nabla) \vec{u}-\nabla p, \quad \quad \quad \quad \quad\text{div} (\vec{u})=0 \)
Navier–Stokes equation
몽지-암페어Monge-Ampère 방정식은 가장 기본적인 완전비선형 방정식으로 헤세 행렬Hessian matrix의 행렬식determinant을 미분 연산자로 사용합니다. 이 방정식의 일종인 최적 운송optimal transport 이론은 물류 이동 비용을 최소화하는 운송법의 연구로 20세기 초부터 매우 중요한 연구 주제였습니다. 실제로 세드릭 빌라니Cedric Villani와 알레시오 피갈리Alessio Figalli가 최적 운송 이론으로 필즈메달을 수상했으며, 레오니트 칸토르비치Leonid Kantorovich는 노벨 경제학을 수상했습니다. 뿐만 아니라 케일러 측량Kahler metric은 복소 몽지-암페어 방정식으로 이를 사용하여 칼라비Calabi 추측을 증명한 싱퉁 야우Shing-Tung Yau도 필즈메달을 수상하였습니다. 이와 같이 몽지-암페어 방정식은 수많은 수학자들이 연구하고 다양한 방식으로 발전시켜온 방정식으로 여러가지 관점의 이론들이 조화를 이루고 있습니다.
\( \det( D^2 u)(x) =f(x) \)
Monge-Ampère equation
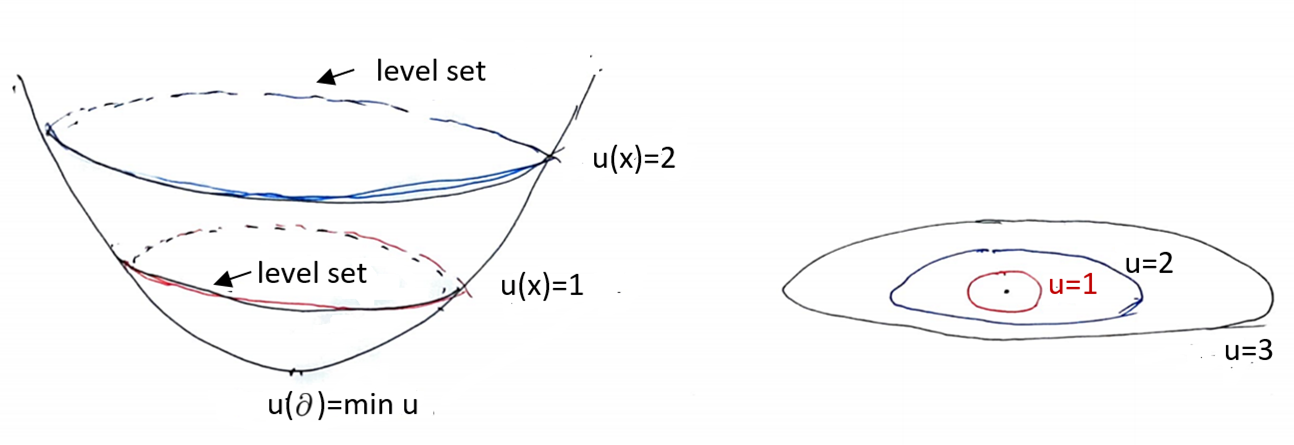
카파렐리 또한 여러가지 새로운 관점을 이론을 몽지-암페어 방정식에 도입하여 1990년대에 역사적인 논문을 여러편 출판했습니다. 그 중 한 가지인 해의 레벨 집합level set의 이심률eccentricity를 이용한 내부 정칙성 이론을 짧게 소개하겠습니다. 기본적인 몽지-암페어 방정식은 볼록한 해를 가집니다. 따라서 해가 최소값을 가진다면 레벨 집합들은 모두 볼록한 닫힌 초곡면이 됩니다. 이러한 볼록 초곡면들은 타원과 같이 생각하며 둥근 구에 가까울수록 이심률이 작고 길게 찌그러질 수록 이심률이 크다고 할 수 있습니다. 카파렐리는 이 레벨 집합이 최소 레벨에 가까워질 수록 이심률이 감소함을 보여서 해의 정칙성을 증명하였습니다. 이는 볼록 기하학을 미분방정식에 응용한 것으로 매우 놀라운 이론의 발명이었습니다.
맺음말
보통 수학 논문은 한 편당 30페이지에서 100페이지에 달하기 때문에, 일 년에 두 편의 논문만 써도 한 권의 책을 쓰는 것과 같습니다. 따라서 한 수학자가 평생 50편 정도의 논문을 썼다면 마치 수학으로 대하소설을 쓴 것과 같습니다. 그런데 처음 언급했듯이 카파렐리는 무려 400여편이 논문을 발표하였고, 심지어 이 논문들의 주제가 너무 다양해서 이 글에서 모두 소개하지 못했습니다. 이것은 그가 혼자 작성한 논문들도 많았지만, 더욱 많은 논문을 공동 연구를 통하여 공동 집필했기 때문에 가능했습니다. 그리고 수많은 동료 수학자들이 그와 함께 연구를 한 것은 그의 수학이 동료들에게 새로운 영감을 주었기 때문이라고 생각합니다. 그는 아벨상 수상 인터뷰에서 자신은 새로운 이론을 설계하기보다 기존의 난제를 해결하는 수학자라고 하였습니다. 하지만 그는 난제를 해결하며 새로운 방식을 도입하기도 했으며, 그 방법론은 다른 이들에게 영감을 주고, 이를 기반으로하는 연구 분야가 새로 생기기도 했습니다. 이처럼 카파렐리는 새로운 길을 열어 많은 이들을 이끌어 온 수학자입니다. 그의 연구로부터 많은 영감을 받은 한 명의 수학자로서 카파렐리의 아벨상 수상을 진심으로 축하합니다.