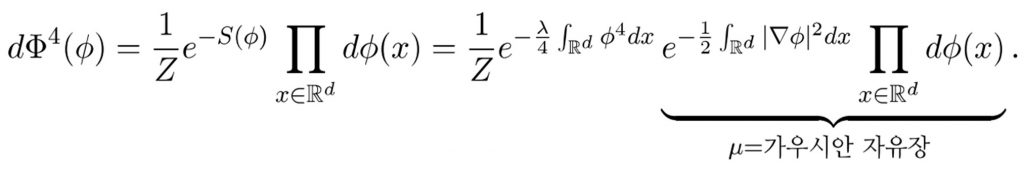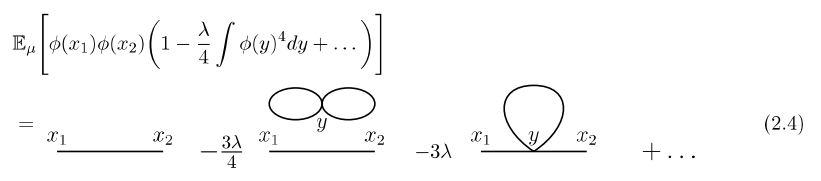편미분 방정식을 이용한 양자장 이론의 건설 [2]: 재규격화와 파인만 다이어그램

1. 수학자와 물리학자에게 있어서의 재규격화

학부 수학 과목 수업을 하다 보면 학생들이 종종 학부 내용을 넘어선 질문을 하는데 그럴 때마다 어떻게 답해야 할지 항상 고민이 많이 됩니다. 이번 학기에 가르치는 학부 3, 4학년 대상인 수업에서 학생들이 대학원 과정이 필요한 내용을 물어보면, 수학적으로 정확하면서도 학부 수준에서 받아들일 수 있는 답을 해줘야 합니다. 학생들이 자연스럽게 받아들여 이해하기 쉬우려면, 때로는 정확한 계산을 일부 숨기더라도, 학생들의 직관과 일치하도록 설명하는 것이 효과적인 경우가 많은 것 같습니다.

지난 연재 글에 따르면, 양자장론에서의 입자 상호작용의 수학적 계산은 무한차원 깁스 측도 ^{Gibbs measure} 를 이용한 경로적분 ^{path integral} 을 통해 이루어집니다. 여기서 중요한 문제점은 이론적 계산에서는 무한차원의 대상인 깁스 측도를 다루므로 무한한 값들이 나타나게 되는데, 실제 관측되는 실험값은 항상 유한하므로 수학적 계산과 실험 결과가 일치하지 않다는 것입니다. 이를 해결하기 위해, 파인만 ^Feynman 과 슈윙거 ^Schwinger 는 최종적인 계산에서 무한대의 값을 숨기는 방법을 개발하게 되는데, 무한대의 값을 실제 경로적분 계산에서 빼주는 것이죠. 이론적 계산 안에서는 분명히 무한대가 존재했지만 최종 결과에서는 무한한 값을 보이지 않게 함으로써, 유한한 값인 실험 결과와 일치시키는 것입니다. 이것을 재규격화^{renormalization} 라고 합니다. 이는 제 수업의 학부생들에게 대학원 수준의 이론적 계산을 일부 숨기면서도, 최종 답을 학부생들의 직관과 일치시키는 과정으로 생각할 수 있습니다.

이러한 무한대를 빼주는 재규격화를 수학자의 입장에선 어떻게 이해할 수 있을까요? 수학자의 입장에서는 실험 결과와 일치시키는 역할을 넘어서, 재규격화를 어떻게 수학적으로 정의하고, 이러한 약속된 개념을 무한차원 깁스 측도의 수학적 건설에 어떻게 사용할 수 있는지 생각해 봐야 합니다. 무한대를 빼주는 재규격화가, 단순히 물리학자들만이 향유할 수 있는 방법이 아닌, 수학자들에게 역시 살아있는 개념으로 존재하기 위해선 우리는 어떤 것들을 생각해야 할까요? 그런 무한대는 정확히 무엇인지, 임의의 무한대를 빼줄 수 있는지 등에 대해 고려해야 합니다. 이번 연재 글에서는 수학자들과 물리학자들의 재규격화에 대한 서로의 방법론을 비교하고, 크게 보면 서로의 방법론이 같은 원리 안에서 이루어진다는 점을 살펴보고자 합니다.

수학적으로 재규격화 필요성에 대한 한 가지 구체적인 예를 들어보도록 하겠습니다. 지난 연재에서 설명했던 것처럼, 무한차원 깁스 측도의 수학적 건설 문제는, 확률적 양자화 ^{stochastic quantization} 를 통해, 특이 확률 편미분방정식 ^{singular SPDE} 을 푸는 것으로 바뀌게 됩니다. 방정식을 푸는 과정에서 재규격화가 필요한데, 만약 방정식 안에서 정확한 양의 무한대를 빼주지 않으면 언제나 해가 0으로밖에 나오지 않습니다. 이를 전문용어로 사소함 ^triviality 이라고 부릅니다. 물리 현상을 기술하는 확률 편미분 방정식의 해가 언제나 0으로 주어진다는 것은 비자연스러운 현상인데, 이를 해결하는 방법은 정확한 양의 무한대를 측정해 방정식 안에서 제거해 주는 재규격화 과정입니다. 여기서 가장 중요한 점은 우리가 임의로 선택하는 무한대가 아닌 정확한 양의 무한대를 제거해 줘야만, 실제 물리 현상을 기술해 주는 방정식의 해에 다가갈 수 있게 된다는 것입니다. 누군가가 자기만의 방식으로 임의의 무한대를 제거해 준다면 확률 편미분 방정식의 해는 계속해서 0인 사소함 ^triviality 결과가 성립하며, 따라서 약속된 방법 안에서 재규격화를 해줘야 한다는 것을 알 수 있습니다.

이러한 재규격화 ^{renormalization} 과정은 확률론과 편미분 방정식의 중요한 이론들인, 라이온스 ^Lyons 의 거친 경로 이론 ^{rough path theory}, 구비넬리 ^Gubinelli 의 통제된 거친 경로 이론 ^{countrolled rough path theory}, 그리고 하이러 ^Hairer 에 의해 이어진 규칙성 구조 ^{regularity structure}에서 중요하게 사용되어, 구성적 양자장론 ^{constructive quantum field theory} 의 핵심 주제인 무한차원 깁스 측도의 수학적 건설을 가능하게 했을 뿐만 아니라, 수학자들과 물리학자들이 재규격화라는 공통된 개념을 공유함으로써 둘 사이의 간극을 좁혀 줬고, 확률론과 편미분 방정식의 개별적 방법론들을 발전시켜 왔습니다. 이러한 점들을 이번 연재 편에서 조금이나마 살펴볼 예정입니다.

2. 섭동이론 ^{perturbation theory} 과 파인만 다이어그램 

지난 연재 글에서 다룬 입자 간의 상호작용 이론을 설명하는 \(\Phi^4\) 양자장론을 잠깐 다시 살펴보겠습니다. 양자역학에 따르면 물리적으로 관심 있는 대상인 관측가능량 (observable)은 다음과 같이 기대값을 통해 계산할 수 있습니다.

여기서 기대값을 취할 때 장 ^field \(\phi\)의 확률분포로 무한차원 깁스 측도 \(d\Phi^4(\phi)\)를 사용합니다. 위의 표현에서 \(d\Phi^4(\phi)\)는 시스템이 상태 \(\phi\)에 있을 확률로 간주할 수 있으며, 함수공간 \(\{\phi:\mathbb{R}^d\to \mathbb{R} \}\) 위에 있는 확률 측도로 이해할 수 있습니다.

무한차원에서의 깁스 측도를 좀 더 쉽게 이해하기 위해, 섭동이론 ^{perturbation theory} 의 아이디어를 다음의 유한차원 \(\Phi^4\) 깁스 측도로 살펴보도록 하겠습니다

\begin{align*} \left<F\right>:=\int_{\mathbb{R}} F(x)e^{-\lambda x^4}e^{-\frac{1}{2}x^2} dx.\end{align*}

여기서 \(x\)는 함수가 아닌 실수를 의미하며, \(\lambda \ge 0\)는 사차 상호작용 ^{quartic interaction}, 즉 \(\lambda x^4\)의 세기를 설명하는 커플링 상수 ^{coupling constant} 입니다. 사차 상호작용 항 \(e^{-\lambda x^4}\)에서 커플링 상수 \(\lambda\)에 대한 테일러 전개를 수행해 주면

\begin{align*} \int_{\mathbb{R} } F(x)e^{-\lambda x^4}e^{-\frac{1}{2}x^2}dx=\int_{\mathbb{R}} F(x) \bigg(\sum_{n=0}^\infty \frac{(-\lambda)^n}{n!} x^{4n} \bigg)e^{-\frac{x^2}{2}}dx = \sum_{n=0}^\infty c_n \lambda^n \end{align*}

위의 섭동 급수 ^{perturbative series} 를 얻을 수 있습니다. 이러한 섭동 급수에서 계수 \(c_n\)들은 가우시안 적분으로 주어지기 때문에 정확하게 계산을 해낼 수 있게 됩니다¹. 따라서

입자 상호작용의 강도를 나타내는 커플링 상수 \(\lambda\) 가 매우 작다면 \(0<\lambda \ll 1\), \(\Phi^4\) 깁스 측도는 위의 섭동 급수 ^{perturbative series} 를 통해 근사할 수 있고, 직접적인 계산들은 우리가 잘 알고 있는 대상인 가우시안 확률측도 \(e^{-\frac{1}{2}x^2 }\)로 이루어 진다는 것입니다 

따라서 섭동 급수의 각 계수 (1) \(c_n\)이 유한하면서 (2) 위의 섭동 급수가 수렴한다면 ^{적어도 매우 작은 \(0<\lambda \ll 1\)에 대해} \(\Phi^4\) 양자장론을 섭동전개 ^{perturbative expansion} 를 통해서 이해할 수 있습니다. 이것이 물리학자들이 \(\Phi^4\) 깁스 측도를 통해 여러 물리적 계산을 수행하는 방법입니다.

위의 섭동이론 ^{perturbation theory} 은 유한차원 깁스 측도를 통해서 이루어 졌는데, 우리가 정말 관심 있는 대상인 무한차원 \(\Phi^4\) 깁스 측도에 대해선 같은 분석을 했을 때 어떠한 현상이 일어날까요? 유한차원에서와 달리 섭동 급수의 모든 계수 \(c_n\)들이 무한대로 발산하는 문제가 생기게 됩니다.

우선 지난 연재에서 살펴봤던 무한차원 \(\Phi^4\) 깁스 측도를 기억해 보겠습니다

위의 표현에서 \(Z\)는 정규화 상수 ^{normalizing constant} 이고, \(d\Phi^4(\phi)\)는 시스템이 상태 \(\phi\)에 있을 확률로 간주할 수 있으며, 해밀토니안 ^Hamiltonian 인 \(S(\phi)=\frac{\lambda}{4} \int_{\mathbb{R}^d} \phi^4 dx+\frac{1}{2}\int_{\mathbb{R}^d} |\bigtriangledown \phi|^2 dx\)는 주어진 시스템의 에너지로 해석할 수 있습니다. \(\lambda \ge 0\)는 입자들간의 사차 상호작용 ^{quartic interaction} \(\int \phi^4 dx\)의 강도를 설명하는 커플링 상수 ^{coupling constant} 입니다. 이전 연재에서 언급했던 것처럼, 위의 \(\Phi^4\) 깁스 측도 표현에서 장들 \(\phi(x)\)의 모임, 즉 함수 공간 \(\big\{\phi:\mathbb{R}^d\to \mathbb{R} \big\}\) 위에서의 넓이나 부피를 의미하는 \(\prod_{x\in \mathbb{R}^d} d\phi(x)\)인 무한차원 르벡 측도 ^{Lebesgue measure} 는 존재하지 않기 때문에, 위의 표현만 본다면 \(\Phi^4\) 깁스 측도는 수학적으로 정의된 대상은 아닙니다. 또한 수학적으로 \(\Phi^4\) 깁스 측도를 이해했다고 하더라도, (2.1) 에서 관측가능량 ^observable 의 기대값은 함수 공간 위에서 적분 ^{functional integral} 으로 주어지기 때문에 이런 적분을 어떻게 다뤄야 할지 생각해 봐야 합니다.

우선 가장 단순한 경우인 입자의 상호작용이 아예 없는, 즉 커플링 상수 \(\lambda=0\) 인 경우를 살펴보도록 하겠습니다. 이 경우 \(\Phi^4\) 깁스측도는 공분산 ^covariance 이 \((-\Delta)^{-1}\)인 가우시안 측도 ^{Gaussian measure} 가 되어 버립니다.

\begin{align*}
\textbf{가우시안 자유장 :} \quad d\mu(\phi)=Z^{-1}e^{-\frac{1}{2} \int_{\mathbb{R}^d} |\bigtriangledown \phi|^2 dx } \prod_{x\in \mathbb{R}^d} d\phi(x).
\end{align*}

무한차원공간 ^함수공간 위에서의 가우시안 자유장은 고전적인 확률 이론을 통해 이미 잘 정의 되어있으므로 수학적으로 명확한 대상입니다. 더욱이나 가우시안 자유장은 이전 연재에서 언급했던 것처럼 양자역학과 상대성이론을 물리적 모순 없이 조화시키는 오스터발더-슈레이더 공리 ^{Osterwalder-Schrader axiom} 를 만족하는 것으로도 알려져 있습니다. 하지만 가우시안 자유장은 \(\Phi^4\) 깁스 측도에서 입자 상호작용의 강도를 의미하는 커플링 상수 \(\lambda=0\)일 때 얻어지므로, 상호 작용하지 않는 입자들의 단순한 시스템을 설명한다는 것을 알 수 있습니다.

여기서 중요한 관찰은 만약 입자 상호작용의 강도를 나타내는 커플링 상수 \(\lambda\) 가 매우 작다면 \(0<\lambda \ll 1\), \(\Phi^4\) 깁스 측도는 가우시안 자유장의 작은 섭동 ^{small perturbation} 으로 간주할 수 있다는 것입니다.

따라서 커플링 상수 \(\lambda\)가 매우 작은 영역을 고려할 때, 입자들의 상호작용 시스템을 설명하는 \(\Phi^4\) 양자장론은 수학적으로 잘 정의 되어있는 가우시안 자유장을 통해 이해할 수 있습니다. 이러한 아이디어를 두 입자 간의 상호작용을 설명하는 상관관계 함수 ^{correlation function} 계산을 통해 좀 더 구체적으로 살펴보겠습니다.

\begin{align*}
\textbf{상관관계 함수} \quad \left<{\phi(x_1) \phi(x_2)}\right>=\mathbb{E}_{\Phi^4}\Big[\phi(x_1)\phi(x_2)\Big]\\= \mathbb{E}_\mu \bigg[\phi(x_1)\phi(x_2) e^{-\frac{\lambda}{4}\int_{\mathbb{R}^d} \phi(x)^4 dx } \bigg]\bigg/ Z.
\end{align*}

여기서 취한 기대값 \(\mathbb{E}_{\Phi^4}\), \(\mathbb{E}_{\mu}\) 각각은 \(\Phi^4\) 깁스 측도와 가우시안 자유장 \(\mu\) 을 통해 계산한 기대값을 의미합니다. 물리학자들은 커플링 상수 \(\lambda\)가 충분히 작을 때, \(e^{-\frac{\lambda}{4}\int_{\mathbb{R}^d} \phi(x)^4 dx}\)를 \(\lambda\)에 대한 테일러 전개를 함으로써 상관함수를 계산합니다 

\begin{align}& \mathbb{E}_\mu \bigg[\phi(x_1)\phi(x_2) e^{-\frac{\lambda}{4}\int \phi(x)^4 dx } \bigg] \\&=\mathbb{E}_{\mu}\Bigg[ \phi(x_1) \phi(x_2)\Bigg(1-\frac{\lambda}{4} \int \phi(y)^4 dy+\frac{1}{2!} \bigg( \frac{\lambda}{4} \int \phi(y)^4 dy \bigg)^2 +\cdots \Bigg) \Bigg] \notag \\&=\sum_{n=0}^\infty a_n \lambda^n. \ \qquad \qquad \qquad (2.2)  \end{align}

이러한 방법론을 사용하는 가장 큰 장점은 위의 섭동 급수 ^{perturbative series} 에서 각각의 \(\lambda^n\) 항에 대한 계수들 \(a_n\)은 수학적으로 명확한 대상인 가우사인 자유장 \(\mu\)의 적분으로 정확히 계산될 수 있다는 것입니다.

하지만 여기서 한가지 문제점은

위 섭동전개 안에서 각 계수 \(a_n\)들은 무한대로 발산하는 항들을 가지고 있다는 것입니다.

파인만 ^Feynman 은 위의 섭동전개 (2.2)에서, 각 계수 \(a_n\)에 숨겨져 있는 발산하는 항들을 편리하게 표현하기 위해 파인만 다이어그램 ^{Feynman diagram} 이라는 그림도구를 사용하게 됩니다.

파인만 다이어그램을 설명하기 위해 가우시안 확률변수가 가지는 중요한 성질 하나를 기억해 보도록 하겠습니다. 윅 정리에 따르면 ^{Wick theorem} 가우시안 확률변수에 대한 곱의 기대값 \(\mathbb{E}\big[ g_1 \cdots g_{2n}\big]\)은 다음과 같이 주어지게 됩니다

\begin{align*} \mathbb{E}\big[ g_1 \cdots g_{2n}\big] = \sum \prod_{k = 1}^n \mathbb{E}\big[g_{i_k} g_{j_k} \big]. \end{align*}

여기서 합 \(\sum\)은 \(\{1, 2, …, 2n\}\)의 숫자를 쌍 \((i_k, j_k)\)으로 나눈 모든 분할에 대해서 행해집니다. 편의를 위해 (2.2)에서 \(\lambda\)에 대한 1차 항인 \(a_1\) 에서 등장하는 기대값 \(\mathbb{E}_{\mu}\Big[\phi(x_1)\phi(x_2) \phi(y)^4 \Big]\)을 살펴보면, 윅 정리에 의해

\begin{align} &=3\mathbb{E}_{\mu}\Big[\phi(x_1)\phi(x_2) \Big]\mathbb{E}_{\mu}\Big[\phi(y)\phi(y) \Big] \mathbb{E}_{\mu}\Big[\phi(y)\phi(y) \Big]\\&\quad+12 \mathbb{E}_{\mu}\Big[\phi(x_1)\phi(y) \Big]\mathbb{E}_{\mu}\Big[\phi(x_2)\phi(y) \Big] \mathbb{E}_{\mu}\Big[\phi(y)\phi(y) \Big] \notag \\ &=3G(x_1-x_2)G(y-y)G(y-y)+12G(x_1-y)G(x_2-y) G(y-y) \qquad\qquad     (2.3)\end{align}

을 얻게 됩니다. 위에서 계산한 상관 함수를 좀 더 편리하게 표현하기 위해 그래픽 도구인 파인만 다이어그램을 도입해 보도록 하겠습니다. (2.3)의 각 항에 있는 \(x_1, x_2, y\)의 점을 그리고 각 \(G\)에 대해 점들을 잇는 선을 그립니다. 이후에는 (2.2)를 다음의 그림으로 표현할 수 있습니다.

(2.4)에서 각 고리 모양은 (2.3)의 \(G(y-y)=G(0)\)를 나타내는데 이는 다름 아닌 지난 연재에서 살펴봤던 가우시안 자유장의 상관관계 함수를 의미합니다.

\begin{equation*} \mathbb{E}_\mu\big[\phi(x)\phi(y)\big]=G(x-y)\approx \begin{cases} -\log|x-y| \qquad &\text{\(d=2\) 일때} \\ \frac{1}{|x-y|^{d-2}} \qquad &\text{\(d\ge 3\) 일때.} \end{cases} \end{equation*}

따라서 (2.4)에서 \(G(y-y)=G(0)\) 를 나타내는 고리들은 모두 \(\infty\)값을 가지기 때문에 수학적으로 잘 정의된 값을 가지지 않는다는 것을 알 수 있습니다. 이러한 현상을 자외선 발산^{ultraviolet divergence}이라고 부릅니다.

양자장론에서 자외선 발산은 파인만 다이어그램의 값이 무한하게 되는 것을 의미합니다.

이러한 자외선 발산으로 인해 \(\Phi^4\) 깁스 측도를 통한 상관관계 함수의 이론적 계산은 언제나 항상 무한대이며 따라서 물리적 사실에 대한 묘사가 불가능하다는 것을 보여주는데, 이를 해결하기 위한 것이 바로 재규격화 ^{renormalization} 입니다. 이러한 방법은 무한대로의 발산을 제거하고 물리적으로 의미 있는 결과를 얻기 위해 사용되는데, 기존 작용량 함수 \(S(\phi)\)에 상쇄항 ^{counter term} 을 도입함으로써 행해집니다.

\begin{align*} & S(\phi)=\frac 12\int |\bigtriangledown \phi|^2 dx+\frac{\lambda}{4} \int \phi^4 dx \\& \qquad \to \qquad S(\phi)=\frac 12\int |\bigtriangledown \phi|^2 dx +\frac{\lambda}{4}\int \big( \phi^4 -{\color{Red} \infty} \cdot \phi^2 \big) dx. \end{align*}

여기서 상쇄항 ^{counter term} 혹은 재규격화 상수 ^{renormalization constant} \(\lambda C^{(1)}+\lambda^2 C^{(2)}+\dots={\color{Red} \infty}\) 는 자외선 발산을 조절하기 위해 추가되는 보정 항을 가리키며 각 차수 \(\lambda^n\)에 따라 알맞은 양의 무한대 \(C^{(n)}=\infty\)를 찾아서 제거해 줘야 합니다. 이러한 보정 항은 기존의 자외선 발산을 제거하면서 최종 결과물을 물리적으로 의미 있는 유한한 값으로 만들어 줍니다.

이러한 재규격화 과정을 통해 상관관계 함수는 가우시안 자유장을 중심으로 한 섭동전개 ^{perturbative expansion} 로 설명할 수 있습니다. 

\begin{align*} \left<{\phi(x_1) \phi(x_2) }\right>=\mathbb{E}_{\Phi^4}\Big[ \phi(x_1) \phi(x_2) \Big] =\sum_{n=0}^\infty a_n \lambda^n. \end{align*}

1960년대부터 활발히 연구되어 온 구성적 양자장 이론에서 수학자들과 물리학자들은 위의 섭동전개 ^{perturbative expansion} 에 대한 다음의 질문에 답하기 위해 많은 노력을 해왔었습니다.

\(\Phi^4\) 깁스 측도를 구성하는 작용량 함수 \(S(\phi)\)에 유한한 혹은 무한한 개수의 재규격화 상수 \(\lambda C^{(1)}+\lambda^2 C^{(2)}+\dots={\color{Red} \infty}\) 를 도입함으로써 섭동 전개 ^{perturbation expansion} 에 있는 모든 파인만 다이어그램 혹은 각 계수 \(a_n\)을 유한하게 만들 수 있을까?

2차원과 3차원의 경우, 유한한 개수의 재규격화 상수를 도입함으로써 섭동 급수 ^{perturbative series} \(\sum_{n=0}^\infty a_n \lambda^n\) 의 모든 차수 \(\lambda^n\)의 계수 \(a_n\)이 유한하다는 것을 보일 수 있고, 4차원의 경우 무한한 개수의 재규격화 상수를 도입함으로써 각 차수의 계수 \(a_n\)이 유한하다는 것을 보일 수 있습니다. 5차원 이상의 경우는 재규격화를 하더라도 섭동이론이 가능하지 않습니다.

이번 절을 마무리하기 전에 한가지 강조할 것은 섭동 전개 ^{perturbative expansion} 에 있는 모든 차수의 파인만 다이어 그램 혹은 각 계수 \(a_n\)이 유한하다고 해서 \(\Phi^4\) 깁스 측도가 수학적으로 정의되었다는 것을 의미하진 않습니다. 수리물리학자 재피 ^Jaffe에 의해 증명된 결과에 의하면, 섭동 급수 ^{perturbative series} \(\sum_{n=0}^\infty a_n \lambda^n\) 의 수렴 반경은 \(\lambda=0\) 이며, 따라서 아무리 작은 커플링 상수 \(\lambda\)를 가져오더라도 섭동 급수는 발산합니다. 그럼에도 불구하고 물리학자들이 양자장론의 여러 계산을 섭동 전개를 통해 수행하는 이유는, 비록 급수가 발산할지라도 아래와 같이, 적절히 큰 \(N\)에 대해 유한한 합 \(\sum_{| n|\le N}\)을 취하면 상관관계 함수를 분석하는데 좋은 근사값을 얻을 수 있으며, 이 값은 여러 실험 결과와 일치하기 때문입니다.

\begin{align*} \left<{\phi(x_1) \phi(x_2) }\right>=\mathbb{E}_{\Phi^4}\Big[ \phi(x_1) \phi(x_2) \Big] \approx \sum_{|n| \le N} a_n \lambda^n. \end{align*}

하지만 무한한 합을 취할 경우, 수학자의 관점에선 위의 섭동 급수 ^{perturbative series} 는 모든 \(\lambda>0\)에 대해 발산한다는 점에서 잘 정의된 수학적 대상이 아닌데, 따라서 \(\Phi^4\) 깁스 측도의 건설은 좀 더 엄밀한 수학적 논의가 필요하다는 것을 알 수 있습니다. 이를 아래 절에서 살펴보겠습니다.

3. 재규격화를 통한 특이 확률 열방정식의 풀이

이전 연재 편에서 살펴봤던 파리지 ^Parisi 그리고 우 ^Wu 의 확률적 양자화 ^{stochastic quantization} 는 \(\Phi^4\) 양자장론의 건설을 특이 확률 편미분 방정식 ^{singular SDPE} 을 푸는 문제로 바꿔준다는 것을 살펴보았습니다. 좀 더 구체적으로, \(\Phi^4\) 깁스 측도 건설 문제는 다음과 같은 \(\Phi^4\)-동역학 모델, 즉 특이 확률 열 방정식 ^{singular stochastic heat equation 2} 을 공부하는 것으로 바뀐다는 것입니다.

\begin{align} \partial_t u – \Delta u + u^{3}-{\color{Red} \infty} \cdot u = \sqrt 2\xi. \ \qquad \qquad \qquad (3.1)  \end{align}

여기서 \(\xi\)는 시간과 공간 \(\mathbb{R}_+\times\mathbb{R}^d\) 상의 (가우시안) 시공간 백색 소음^{space-time white noise} 을 의미합니다³.

간단히 확률적 양자화의 아이디어를 다시 기억해 보면, 지난 연재 편에서 언급했던 특이 확률 열 방정식의 에르고딕 ^ergodicity 성질에 의해 균형 분포 ^{equilibrium distribution} 는 다음과 같이 주어지게 됩니다.

이는 초기 값 \(u(0)\)에 대한 확률 분포 Law(u(0))를 임의의 확률 분포로 설정하더라도, 이전의 기억을 완전히 잃으면서, 충분한 시간이 흐르면 확률 편미분 방정식 (3.1) 의 해 \(u(t)\)는 \(\Phi^4\) 깁스 측도로 수렴하게 되어 있습니다. 따라서 \(\Phi^4\) 양자장론의 수학적 건설은 확률 편미분 방정식 (3.1)의 대역 해 ^{global solution} 를 찾는 문제로 바뀌게 됩니다.

특이 확률 열 방정식 (3.1) 의 해를 찾는 과정은 이전 절에서 살펴봤던 섭동이론 ^{perturbation theory} 과 파인만 다이어 그램을 ^{Feynman diagram} 을 기반으로 합니다. 잠깐 섭동이론의 핵심 아이디어를 생각해보면, 수학적으로 정의되어 있지 않은 \(\Phi^4\) 깁스 측도를, 아래 표현과 같이, 정확히 정의되어 있는 가우시안 장의 작은 섭동 ^{small perturbation} 으로 가정하고

\(\Phi^4\) 깁스 측도=가우시안 자유장+작은 오차,

가우시안 자유장 ^{Gaussian free field} 을 중심으로 섭동전개 ^{perturbative expansion} \(\sum_{n=0}^\infty a_n \lambda^n\)를 수행하는 것이었습니다.

마찬가지로, 우리가 위에서 살펴본 특이 확률 편미분 방정식 (3.1) 을 이해하는 가장 간단한 방법은 명확히 풀 수 있는 선형 확률 편미분 방정식의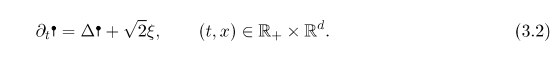작은 섭동 ^{small perturbation} 으로 가정하여 해석하는 것입니다. 여기서 고려해야 할 것은 비선형 확률 편미분 방정식 (3.1) 이 언제나 선형 확률 편미분 방정식 (3.2) 의 작은 섭동 ^{small perturbation} 으로 가정할 수 있는지입니다.

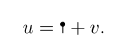만약 비선형 \(\Phi^4\) 방정식 (3.1) 의 해를 선형 방정식 (3.2) 을 중심으로 한 작은 섭동 ^{small perturbation} 으로 분석할 수 있다면⁴, 비선형 \(\Phi^4\) 방정식의 해 \(u\)를 선형 방정식의 해 의 작은 변동 \(v\)로 나타낼 수 있을 것입니다.따라서 \(v\) 에 대해 \(\Phi^4\) 방정식을 다시 써보면

을 얻게 됩니다.

여기서 한가지 주목할 사실은 선형 확률 편미분 방정식 (3.2)의 해  는 가우시안 자유장을 확률 분포로 가진다는 것입니다. 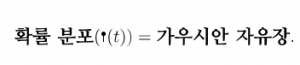따라서, 이전 절의 섭동전개 ^{perturbative expansion} (2.2), 혹은 파인만 다이어그램들 (2.4) 에서 가우시안 자유장을 포함한 항들이  자외선 발산문제 ^{ultraviolet divergence} 를 가졌다는 것을 떠올려 볼 때, 같은 이유를 통해 (3.3) 에 있는 과 은 무한대 값을 가진다는 것을 보일 수가 있습니다. 이러한 자외선 발산하는 항들에서 재규격화 ^{renormalization} 를 통해 알맞은 양의 무한대 를 제거해 준다면 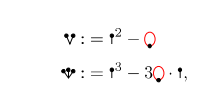과 같은 대상들을 잘 정의 할 수 있게 됩니다.

여기서 재규격화 ^{renormalization} 과정은 무한대로 발산하는 파인만 다이어그램들 을 빼줌으로써 기존에 정의할 수 없던 대상들 을 다루게 해줍니다. 

이렇게 새롭게 얻어진  을 통해 방정식  (3.3) 을 다시 써준다면

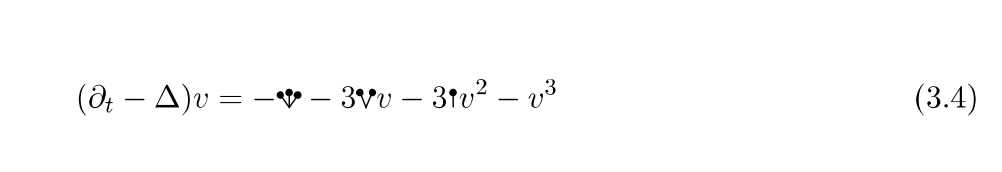
을 얻게 되고, 남은 과정은 \(v\)에 대해서 새롭게 얻어진 방정식 (3.4) 를 푸는 것입니다. 적어도 2차원 공간에서는 이런 과정, 즉 (i) 원래 방정식을 재규격화 ^{renormalization} 하고, (ii) 그런 다음 나머지 \(v\)에 대한 방정식을 풀 수 있음이 잘 알려져 있습니다. 이러한 과정은 거친 경로 이론 ^{rough path theory} 에 기반을 두는데, 이를 요약하면 다음과 같습니다⁵. 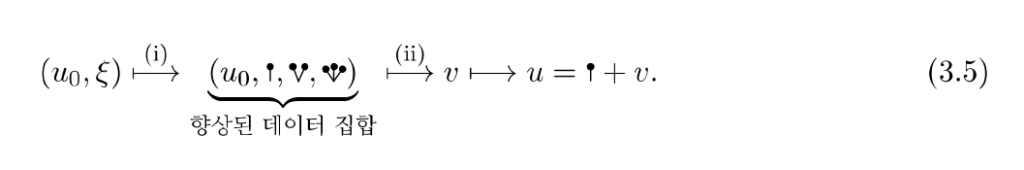(i) 첫 번째는 재규격화 ^{renormalization} 향상된 데이터 집합 ^{enhanced data set} 을 생성하는 과정입니다. (ii) 두 번째는 새로운 데이터 집합에서 해로 이어지는 연속 해 사상 ^{continuous solution map} 을 편미분 방정식의 방법론을 통해 건설하는 것입니다.

따라서  를 주어진 데이터로 간주하여, 확률적 대상들  의 경로를 고정한 다음에 \(v\)에 대한 편미분 방정식 (3.4) 를 풀게 됩니다.

3차원 공간에서는 위에서 형성된 향상된 데이터 집합  과 나머지 항 \(v\)로는 해를 구할 수 없게 됩니다. 이를 해결하기 위해서는 더 복잡한 재규격화 ^{renormalization})과정이 필요하며, 더 많은 확률적 대상이 도입되어야 합니다 . 더 나아가, 나머지 항 \(v\)를 더 세밀하게 분해하여 \(v=X+Y\)로 나누고, \(X\)와 \(Y\)가 만족하는 편미분 방정식 시스템을 경로별 분석을 통해 풀어내야 합니다. 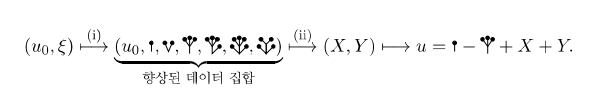하이러와 구비넬리의 주요 업적은 위의 (i) 확률 분석 ^{stochastic analysis} 을 통한 재규격화 ^{renormalization}  과정과 (ii) 경로별 분석 ^{pathwise analysis} 을 보다 체계적으로 개발하여, 3차원 공간상에 있는 \(\Phi^4\) 방정식뿐만이 아니라, 아래임계 ^subcritical 조건을 충족하는 모든 특이 확률 편미분 방정식 ^{singular SPDE} 에 대한 풀이법을 체계적으로 제시한 것입니다.

4. 연재를 마치며

첫 번째 연재 편에선 무한차원 깁스 측도의 수학적 건설 문제를 확률적 양자화를 통해 어떻게 특이 확률 편미분 방정식으로 바꾸어 해결할 수 있는지 살펴봤습니다. 이번 연재 편에선 물리학자들이 섭동이론, 파이만 다이어그램, 그리고 재규격화를 사용해 \(\Phi^4\) 깁스 측도를 어떻게 이해하는지, 마찬가지로 수학자들 역시 섭동이론에 기반한 아이디어와, 파인만 다이어그램, 그리고 재규격화를 이용하여 어떻게 특이 확률 편미분 방정식을 푸는지 간략히 살펴보았습니다. 두 연재에서는 수학자들이 양자장론의 \(\Phi^4\) 깁스 측도를 특이 확률 편미분 방정식을 통해 어떻게 분석하는지에 대해서 주로 다뤘지만, 역으로 \(\Phi^4\) 깁스 측도를 통해서도 특이 확률 편미분 방정식에 대한 이해를 끌어낼 수 있습니다.

예를 들면, 제가 최근에 연구하는 주제인, 낮은 온도 영역에서 (1) \(\Phi^4\) 깁스 측도가 가장 낮은 에너지 상태로 집중되는 현상 ^{큰 수의 법칙} 과 (2) 적절한 스케일링 하에서 \(\Phi^4\) 깁스 측도가 가우시안 측도로 수렴하는 현상 ^{중심 극한 정리} 은, 저온 영역에서 확률 편미분 방정식의 장시간 행동을 예측하게 해줍니다. 이러한 \(\Phi^4\) 깁스 측도의 (1) 큰 수의 법칙과 (2) 중심 극한 정리를 보이는 과정에서 섭동이론이과 파인만 다이어그램은 중요하게 사용됩니다.

두 편의 연재를 통해 물리학에서 등장하는 깁스 측도, 섭동이론, 재규격화, 그리고 파인만 다이어그램을 수학자들이 어떻게 이해하면서 사용하는지에 대해 독자분들께 조금이나마 전달되었기를 바라며, 글을 마칩니다. 

연재글

편미분 방정식을 이용한 양자장 이론의 건설 [1]: 무한 차원 깁스 측도와 확률 편미분방정식