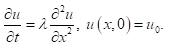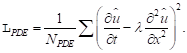물리 기반 신경망은 전통적 수치해석을 대체할 수 있을까? [1] 원리와 장점

1997년, Lagaris, Likas, Fotiadis에 의해 인공신경망^{Artificial Neural Network, ANN}을 이용한 상미분방정식^ODE와 편미분방정식^PDE을 계산하는 방법이 처음 세상에 공개된 이후[1], 그리고 2012년 알렉스넷^Alexnet과 2016년 알파고 등장 이후 ANN, 나아가 딥러닝을 이용한 다양한 종류의 물리, 공학에서 미분방정식 형태로 기술되는 문제를 신경망 학습을 통해 해결하는 방법론은 지난 20여년 간 지속적으로 발달해 왔다.[2] 사실 대부분의 물리 혹은 공학 문제의 풀이는 결국 시간, 공간에서 기술되는 어떤 현상이나 시스템을 규정하는 특정 변수가 어떻게 바뀌는지를 모사하고 그것을 예측하는 것으로 수렴한다. 수학적으로는 이러한 모사와 예측은 대체로 미분방정식의 해를 구하는 것으로 대체된다. 따라서 ANN을 이용한 ODE, PDE 계산 알고리즘이 고도화되면 이를 물리학이나 공학에서 계산하고자 하는 난제 풀이에 적용하려는 것은 예상할 수 있는 전개일 것이다. 그렇지만 ANN을 단순히 미분방정식 풀이에 적용하는 방법 그 자체는 이른바 ‘물리 기반 신경망´^{Physics-informed neural network, PINN}의 핵심은 아니다. PINN의 핵심이자 고유한 장점은 물리적 시스템이나 어떤 현상의 지배방정식으로 작동하는 미분방정식의 해를 신경망 기반 함수로 모사하고자 할 때, 그 함수의 최적 형태를 찾는 과정에 있다. 특히 우리에게 잘 알려진 물리 법칙들을 일종의 제약 조건처럼 만들어, 그 법칙에서 벗어나지 못 하게끔 강제하는 것에 있다.

일단 PINN을 이해하기 전에, 다소 식상하긴 하지만 전형적인 딥러닝 작동 방식부터 알아보자. 딥러닝은 복잡한 입력 조건 하에서 최대한 정확하게 혹은 고품질의 출력을 생성하거나 예측하기 위한 고도로 자동화된 통계적 해석 방법으로 볼 수 있다.[3] 기본적으로 딥러닝은 신경망에 내재된 이른바 은닉층^{hidden layer}를 이루는 파라미터의 조정, 즉, 학습에 많은 데이터를 요구한다. 좋은 데이터가 많을수록 일반적으로 출력의 품질, 즉, 해석과 예측 성능은 강화된다. 예를 들어 중력의 법칙, 나아가 행성의 공전에 대한 역학적 관계를 전혀 모르고 있는 상황이라고 하더라도, 시간에 따른 행성들의 공전 관측 데이터가 충분히 확보되어 있다면, 잘 훈련된 딥러닝 알고리듬을 통해 천문학을 전혀 모르는 사용자라고 해도 태양계 모든 행성들이 앞으로 몇 백만년 간 몇 번이나 서로 일렬로 배치될 수 있을지를 상당히 정확하게 계산할 수 있다. 예측 자체에만 초점을 맞춘다면 이러한 접근 방식은 어쨌든 꽤 괜찮은 결과를 보장하므로 상당히 만족스럽게 보일 수도 있다. 그렇지만 결국 중력의 법칙이나 행성 공전에 관한 역학의 메커니즘 이면에 있는 물리 법칙, 그리고 그것을 수학적으로 추상화한 이론 체계는 알 수 없는 채로 남아 있을 것이다. 이는 보다 일반적인 관점에서는 ‘블랙박스’로서의 딥러닝 혹은 딥러닝의 해석^{interpretability} 능력 한계라는 잘 알려진 문제로 귀결된다. 해석 능력의 한계는 딥러닝만으로는 추상화 혹은 일반화할 수 있는 수준의 이론이나 모델을 만들기 어렵다는 이야기가 된다. 우리가 중력의 법칙을 모른 채로, 태양계 행성들의 공전 궤도 특성만 잘 설명할 수 있는 딥러닝 기반의 어떤 소프트웨어만 가지고 있는 상황을 가정해 보자. 그렇다면 우리는 태양계를 벗어날 수 있는 우주선의 탈출 속도나 행성의 공전/자전의 각운동량을 이용하여 우주선의 추진력을 강화하는 플라이-바이^Fly-by 항법 등을 생각해내고 그것을 고도화된 수준으로까지 철저하게 계산하며 설계할 수 있을까? 이러한 응용은 학습된 딥러닝이 아닌 일반화된 법칙을 인간이 발견해야 가능한 것들이다. 뉴턴이 지표로 떨어지는 사과를 관찰했지만, 그것을 일반화한 만유인력 법칙을 수학적으로 기술하는 것까지 나아가지 못했다면 인류는 고전역학을 훨씬 늦게 수학적으로 정리했을 것이고, 아마 우주로 진출하는 시기 역시 한참 뒤로 밀렸을 것이다.

딥러닝은 그 출력물이나 생성된 데이터의 품질, 주어진 데이터 공간 내에서의 예측력은 뛰어나지만, 그것을 기반삼아 보다 일반화된 모형 생성이나, 이론 등으로 나아가기 매우 어렵다는 것은 딥러닝을 이용한 과학 혹은 공학 연구에서 늘 찜찜한 부분으로 작동한다. 뉴턴이 떨어지는 사과를 보며 만유인력 법칙을 떠올렸고, 그것을 수학적으로 정리했으며, 그를 위해 미적분을 발명하고 이를 일반화하여 행성의 공전 궤도를 설명하며 나중에는 헬리 혜성의 공전 주기까지 예측할 수 있는 수준으로 도달할 수 있었던 원동력은 무엇일까? 그것은 이른바 서로 관련이 없어 보이는 현상들을 관통하는 하나의 물리 법칙을 정의하고 그것을 수학적으로 추상화할 수 있었기 때문이다. 딥러닝의 설명 가능성의 한계가 물리 법칙으로의 추상화 가능성에 대한 한계로 인해 생기는 것이라면, 반대로 생각할 수도 있지 않을까? 즉, 적어도 우리가 알고 있는, 그리고 아직까지는 매우 잘 작동하는 것처럼 보이는 수많은 물리 법칙 자체를 딥러닝이 학습하도록 만든다면, 적어도 물리 법칙에 기반을 둔 복잡한 데이터의 해석이나 예측, 나아가 그것의 일반화가 더욱 명확해지지 않을까? 설사 학습할 데이터가 부족하다고 해도, 물리 법칙만 확실히 알고 있다면 그로부터 시뮬레이션 등을 통해 학습할 데이터를 충분히 더 많이 만들 수 있지 않을까? 심지어 불균형한 데이터 밖에 없는 상황이라고 하더라도, 물리 법칙을 알고 있다면 그 빈 공간을 채워 넣을 수 있지 않을까? 여기서 창안하여 시작된 것이 PINN이라고 볼 수 있다.

PINN의 작동 원리

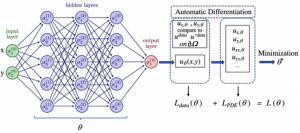
일단 PINN의 원리를 살펴보자. PINN도 이름에 NN이 포함되어 있으므로 일단 신경망이후, NN로 통칭을 사용한다. 여기서 NN은 물리 법칙으로 설명하고자 하는 일종의 함수다. 딥러닝에서 흔히 사용하는 합성곱 신경망^{convolution NN (CNN)}이나, 환류 신경망^{recurrent NN (RNN)}, 그래프 신경망^{graph NN (GNN)}, 최근에 많이 활용되는 트랜스포머^transformer류의 생성형 모델 등이 다 쓰일 수 있다. 그래서 NN은 PINN에서는 일종의 본원적 함수 근사기^{universal function approximator}로 불리기도 한다. 이러한 함수 근사기를 이용하여 설명하고자 하는 데이터는 어떤 시스템이나 현상에서 우리가 보고자 하는 어떤 변수의 시간, 공간에 따른 분포 데이터다. 예를 들어 긴 금속 막대의 한쪽 끝을 토치로 달구어 뜨겁게 만든다면 시간이 지남에 따라 그 금속 막대의 온도는 점점 높아질 것이다. 여기서 우리가 보고자 하는 것은 금속 막대의 특정 지점에서 특정 시간에서의 온도가 몇 도이냐는 것이다. 이런 문제는 물리학과나 공대 학부 수준에서는 주로 확산방정식^{diffusion equation}이나 열방정식^{heat equation}을 배우면서 만나는 흔한 케이스다. 시간과 공간, 그리고 공간 자체도 3차원 공간이므로 이 열방정식 문제는 기본적으로 다음과 같은 간단한 편미분방정식으로 표현할 수 있다(편의상 공간은 1차원만 고려).

위 방정식에서 는 무차원화된 온도, 와 는 각각 무차원화된 시간과 공간을 나타내며, 온도의 초기값^{initial value}는 로 주어져 있다고 가정했다. 기존의 수치해석 방법으로는 이러한 편미분방정식은 주로 유한차분법^{finite difference method, FDM}나 유한요소법^{finite element method, FEM}같은 방법을 이용하여 계산한다. FDM과 FEM의 기본적인 접근 방식은 ‘유한’이라는 수식어에서도 볼 수 있듯, 다루고자 하는 시스템의 연속 공간을 유한한 개수의 작은 점 혹은 셀^cell 같은 기본 요소로 이루어진 이산 공간으로 나누어(이러한 작업을 Meshing이라고 한다.), 각 점에서의 변수(위 방정식에서는 u)의 차분 관계와 구배 벡터^{gradient vector}를 계산한 후 시간에 따라 업데이트하는 것이다. FDM의 경우 주로 직사각형, 혹은 직육면체, 실린더 같이 규칙적이고 대칭성을 갖는 형태의 공간으로 표현될 수 있는 시스템을 모사하는데 적합하다. 그 시스템 내부와 겉면(즉, 경계)에 규칙적으로 배열된 각 격자점에 위치한 변수 값들은 매클로린 급수^{Maclaurin series}에 기반한 미분 연산자들로 연결되고, 이는 수학적으로는 행렬 형태로 표현된다. 이 행렬에 각 지점에서의 변수 값을 저장한 초기값을 벡터 형태로 만들어 위에서 구축한 행렬 연산자에 입력하면 그 다음 시점에서의 벡터값이 나온다. 이를 통해 규칙적인 간격의 시점마다 각 지점에서의 변수값을 계산할 수 있다. FEM의 경우, 미분방정식을 적분형으로 표현한 다음, 선형시스템으로 변환하여 역행렬을 구하는 방식으로 이산 공간에 흩어진 각 요소에서의 변수 값을 계산한다. 반면 PINN에서는 입력값으로 특정 위치와 특정 시간의 정보를 받아 NN를 구성하는 노드의 특징(예를 들어 가중치 등)을 업데이트하여 최적화함으로써 u값을 추정한다. 이러한 NN 함수 근사기는 물리법칙에서 이미 알고 있는 지배 방정식을 위배하지 않도록, 그 오차를 최소화하는 방향으로 계속 업데이트되며 최적화된다. 따라서 PINN에서는 FEM, FDM 같은 meshing 기법을 사용할 필요가 없으며, 최적화 과정에서 참고할 수 있는 몇 개의 시공간 포인트들(이를 collocation points라고 부른다.) 만 입력 값으로 필요할 뿐이다. 이 때문에 고전적인 FEM, FDM이 계산해야 하는 시공간이 늘어나면 그에 비례하여 연산량이 증가하는 부담이 생기는 것에 반해, PINN은 일단 물리법칙에 최대로 근접한 NN 함수 근사기가 학습 완료되면 어떤 입력값을 받든, 근사치를 계산할 수 있으므로, 그러한 부담에서 비교적 자유롭다.

PINN에서 최적화하고 하는 손실 함수는 크게 두 가지로 구성된다. 첫번째 손실 함수는 주어진 데이터 ()와 생성된 데이터 () 사이의 오차에 대한 것이다. 여기서 ‘주어진 데이터’는 보통 해석적 해가 잘 알려진 PDE의 경우에는 얼마든지 쉽게 많이 만들 수 있지만, 그렇지 못한 경우라면 전통적인 FDM, FEM, Runge-Kutta solver, 나아가 스펙트럴 방법(spectral solver) 같은 수치해석 방법을 이용하여 만들어내야 한다.

참고로 는 신경망 기반 함수 근사기 와 초기 조건 ()을 이용하면 다음과 같이 표현될 수 있다.

생성된 데이터와 주어진 데이터 사이의 오차는 공간 내의 모든 지점에 대해 계산될 수 있으며, 이를 모두 고려하면 다음과 같은 손실 함수^{loss function}로 표현될 수 있다.

두번째 손실 함수는 생성된 데이터가 지배방정식을 만족하지 못 하는 경우에 발생하는 오차에서 나온다. 이는 다음과 같은 손실 함수로 표현될 수 있다.

위 방정식에서 볼 수 있듯, 물리 법칙은 여러 개 도입될 수 있으며, 따라서 보다 복잡한 물리 현상이나 시스템 (즉, 두 개 이상의 변수가 필요한 현상이나 시스템)으로도 쉽게 확장할 수 있다. 두 손실 함수는 적절한 가중치 와 를 고려하여 다음과 같이 하나의 손실 함수로 합쳐질 수 있다.

여기에 몇 가지 오차 요인에서 비롯되는 손실 함수를 추가할 수도 있다. 이는 대부분 경계조건^{boundary conditions}에서 비롯되는 손실 함수 와 미분-대수방정식^{Differential-Algebraic equation(DAE)}에서 비롯되는 손실 함수 등이다. 따라서 보다 포괄적인 손실 함수는 다음과 같이 확장될 수 있다.

이렇게 일반화된 손실 함수를 NN이 학습하게 하면 손실 함수에서 계산되는 오차를 최소화할 수 있고, 그 오차가 미리 설정된 기준보다 작아지게 되면 실제 해에 상당히 근접한 해를 얻은 것으로 간주할 수 있다. 이는 결국 PINN도 최적화 문제로 환원됨을 의미한다. 이러한 최적화 과정 자체는 딥러닝에서 잘 알려진 손실 함수 최소화 방식을 사용하면 된다. 주로 사용되는 방식은 ADAM[5]과 준-뉴턴 L-BFGS^{quasi-Newton limited-memory Broyden-Fletcher-Goldfarb-Shannon} [6] 등이다. 특히 L-BFGS 방법은 노이즈가 많은 데이터나 합성 데이터에서도 잘 작동한다는 것이 알려져 있기 때문에, 확률론적 미분방정식^{stochastic DE, SDE} 기반의 PINN을 구성할 때 더욱 유용하다.

PINN의 적용 사례

PINN이 잘 작동하는 케이스는 위의 사례에서 알아본 열방정식 같은 잘 설정된 문제^{well-posed PDE} 기반의 사례들이다. 즉, PDE의 해가 존재하며, 그 해가 유일하고, 초기값의 변화에 대해 방정식의 해가 연속적으로 부드럽게 변하는 특성 등을 갖춘 문제들이다. 예를 들어, 가장 간단한 PDE 중 하나인 2차원 라플라스 방정식^{Laplace equation}의 사례를 살펴보자. 방정식이 대상으로 삼는 2차원 도메인 을 생각할 수 있고, 그 도메인의 경계를 규정하는 경계조건으로 디리클레 경계조건^{Dirichlet boundary condition}이 주어져 있다고 가정해 보자. 그러면 이 방정식과 경계조건은

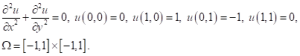
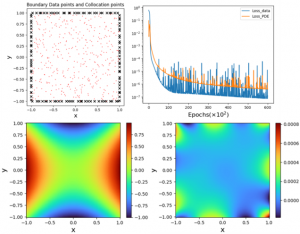
같이 표현할 수 있다. 참고로 이 방정식의 해석적 해는 쉽게 구할 수 있으며 다. 그림 2에 보인 바와 같이, 학습 데이터를 확보하기 위해 우리는 주어진 도메인과 그 경계에 대해 사전에 정한 만큼 collocation points를 랜덤하게 고를 수 있다. 예를 들어 그림 2에서는 경계에서 120개, 내부 공간에서는 400개의 데이터 포인트를 랜덤하게 고른 결과를 보였다. 다섯개의 은닉층(hidden layer, 매 layer에는 20개의 node 배치)으로 구성된 NN을 활용하여 L-BFGS 최적화 알고리듬에 따라 손실 함수를 최소화하면 그림 2에 보인 바와 같이 PDE 손실 함수와 데이터 손실 함수에서 계산되는 오차가 각각 10,000 epoch 정도만에 빠르게 감소되는 것을 확인할 수 있다. 여기서 주목할 부분은 데이터 손실 함수보다 PDE 손실 함수의 오차 감소폭이 작다는 것이다. 이는 PINN에서 PDE 손실 함수에 조금 더 가중치를 두면서 손실 함수를 설계할 필요가 있음을 의미하는 것이기도 하다. 그림 2에 보인 바와 같이 PINN이 충분히 학습된 경우에도 여전히 오차는 존재하며, 대부분의 오차는 주로 도메인의 경계 혹은 경계 근처에서 생성되는 것을 확인할 수 있다. 이는 경계와 경계로부터 일정 거리 이내에 있는 collocation point가 다른 지역보다 많은 경우에 더욱 잘 발현되며, 기본적으로 경계 근처에서 수치 불확실성이 증폭되는 경사하강법^{gradient descent method}만의 고유한 특징 때문이기도 하다.

이는 전통적인 FEM, FDM 방법에 비해 PINN이 도메인의 경계 근처에서 수치 오차에 상대적으로 약하다는 특징을 갖게 만드는 주원인이기도 되기도 한다. 전통적인 수치해석 방법 중에서도 FDM은 규칙적인 메쉬^mesh를 이용하는데, 유한 차분의 원리 상, 메쉬를 더 작게 만들수록 오차는 더 빨리 작아질 수 있다. 예를 들어 메쉬의 크기를 반으로 줄이면 오차는 1/4로 줄어든다(이를 parabolic scaling 이라고 부른다.). 그렇지만 PINN에는 규칙적인 격자점도 없으며, 대신 랜덤하게 선택한 collocation point를이용하는 일종의 통계 방법론만 존재할 뿐이다. 즉, 2차원 도메인 내부에 collocation points를 4배로 늘린다고 해서(즉, 포인트들 간 평균 거리를 절반으로 줄인다고 해서) 수치 오차가 1/4로 줄어드는 것은 아니라는 뜻이다. 또한 FDM은 메쉬가 좀 큰 경우에도 아주 정확하지는 않지만 꽤 정답에 근접하는 해를 보여주는 반면, PINN은 내부 collocation points가 충분하지 않은 경우에는 오차가 충분히 줄어들기도 전에 수렴하는 경향을 가지므로, 오류를 포함한 해를 피하기 위해서는 충분히 많은 숫자의 collocation point을 도입해야 한다. 문제는 그 ‘충분한’ 숫자가 얼마나 많아야 충분한지는 처음부터 알 수는 없다는 것이다. 또한 기본적으로 NN을 이용하므로 충분한 숫자의 은닉층과 충분한 숫자의 layer 당 node가 필요하지만, 이 역시 처음부터 그 필요 규모가 얼마나 될지 추정하기는 쉽지 않다. 심지어 너무 많은 은닉층과 node는 얻은 해의 정확도를 오히려 악화시키는 경우도 있다.[7] 따라서 PINN을 이용하여 전통적인 수치해석 방법보다 경계에서의 오차를 더 작게 만들려면 더 엄격한 오차 허용 기준이 필요하며, collocation points 설정에도 더 많은 시행착오가 필요하고, 일반적인 NN보다 더 오래 학습시켜야 할 수도 있으며, 따라서 전통적인 수치해석보다 해를 얻는데 대개 더 많은 시간이 소요된다.

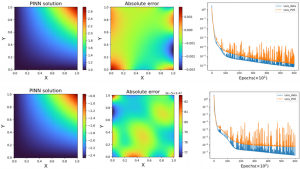
푸아송 방정식^{Poisson equation}의 경우, PINN이 경계조건의 종류 별로 얼마나 다른 오차 특성을 보여주는지 확인할 수 있는 좋은 사례가 된다. 그림 3에 보인 계산 결과는

같은 2차원 푸아송 방정식과 정사각 도메인에 대해, 각각 디리클레 경계조건 (윗줄) 노이만 경계조건(Neumann boundary condition, 아래줄)을 가정하여 계산한 결과를 보여준다. 그림에서 볼 수 있듯, 디리클레 경계조건의 경우에는 주로 경계에서의 수치 오차 증폭이 일어남을 확인할 수 있지만, 노이만 경계조건의 경우는 경계뿐만 아니라 collocation points 밀도가 상대적으로 작은 영역에서의 오차도 충분히 커질 수 있음을 확인할 수 있다. 특히 노이만 경계조건의 경우에는 디리클레 경계조건의 경우보다 NN의 학습이 진행될수록 더 작은 수치 오류로 수렴하고 있음에도 불구하고, 도메인 내부 공간에서의 수치 오차는 사라지지 않는 특성을 보여준다. 이는 PINN을 PDE 계산에 활용하는 경우, 허용할 수 있는 오차의 절대값 자체가 PINN에서 얻은 해의 물리적 정확성 혹은 정합성 여부를 판별하는 유일한 기준이 될 수 없음을 보여준다.

이렇게 PINN은 physics, 즉, 수학적 방정식과 조건들로 구성될 수 있는 모델만 확실하다면 이론적으로는 모든 문제에 대해 적용될 수 있을 것이다. 그렇다면 PINN은 기존의 이산수학 방법론 기반의 수치해석을 모두 대체할 수 있을까? PINN에서 예측되는 값들은 얼마나 믿을 수 있는 것일까? 지배방정식이 규약조건으로 끊임없이 작용한다고 하더라도, 시스템 전체에서 예측되는 값들은 과연 얼마나 정확한 것일까? 2부에서는 이에 대한 내용을 조금 더 상세하게 알아보도록 하자.