[8월의 퍼즐해설] N등급 충명 소환술

아래는 KPP 한동규님의 분석을 바탕으로 작성된 풀이입니다.

1.합성수 등급 충명을 소환하려 할 때 도움이 되는 재미있는 사실이 있다.만약 이 의 배수고 등급 충명을 소환할 수 있다면 등급 충명도 소환할 수 있다. 등급 충명을 소환할 수 있는 양초 조합을 찾은 다음 모든 양초의 번호에 를 곱하면 된다.

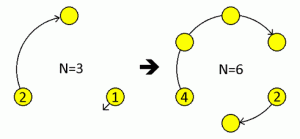
6=2×3이므로 2등급 충명이나 3등급 충명을 소환할 수 있는지를 먼저 따져 보자. 2등급 충명을 소환하는 방법은 없는데, 0번 양초를 켤 방법이 없기 때문이다. 반면 3등급 충명을 소환하는 방법은 한 가지 존재한다. 바로 1번과 2번 두 양초 모두에 토글 의식을 진행하는 것이다.

이를 사용해 6등급 충명을 소환하는 방법을 찾을 수 있다. 일 때 가 답이었으므로, 일 때는 모든 양초의 번호에 2를 곱한 가 답이다. 즉 2번과 4번 양초에 토글 의식을 진행하면 된다.

N이 합성수일 때 사용할 수 있는 이 합성수 전략은 분명 흥미로운 전략이지만, 이 전략만으로 모든 방법을 찾을 수 있다고 확신할 수는 없다.

–

2.7등급 충명을 소환하는 방법은 쉽게 찾을 수 있다. 1번 양초에 토글 의식을 진행하면1번 양초가 켜진다. 2번 양초에 토글 의식을 진행하면2, 3번 양초가 켜진다. 4번 양초에 토글 의식을 진행하면 4, 5, 6, 0번 양초가 켜진다. 따라서 답은 다. 이를 확장하여, 등급의 충명을 소환할 때는 모든 )번 양초들에 토글 의식을 진행하면 된다는 것을 쉽게 알 수 있다.

사실 7등급 충명을 소환하는 방법은 하나가 더 있다. 바로 , 즉 모든 양초에 토글 의식을 진행하는 것이다. 왜 이것이 가능한지는 계속 읽어 보자.

–

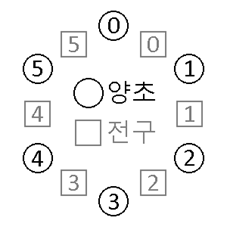
3.이제 조금 더 깊은 관찰을 하기 위해서 이 문제를 수학적으로 동등한 다른 문제로 바꾸어 생각하자.양초 사이사이마다 전구를 하나씩 놓는다. 각 전구는 양쪽에 있는 양초의 상태가 서로 다르면 켜지고, 같으면 꺼진다.

아래 그림과 같이 번 양초와 그 다음 양초 사이에 놓은 전구를 번 전구라고 하자. 그러면 번 양초에 토글 의식을 진행하는 것은 번 전구와 번 전구의 상태를 바꾸는 (켜져 있으면 끄고 꺼져 있으면 켜는) 것이고, 나머지 전구들은 가만히 두는 셈이 된다.

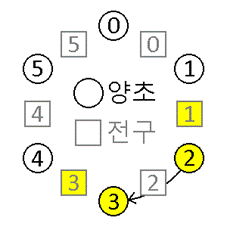
예를 들어 아래 그림과 같이 2번 양초에 토글 의식을 진행하면 번 전구와 번 전구만 상태를 바꾸게 된다.

당신의 목표는 모든 양초를 켜는 것이므로 최종적으로 모든 전구는 꺼져 있어야 할 것이다.

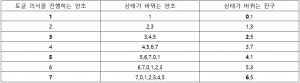
짝수 등급 충명을 소환하려 하는 경우를 관찰해 보자. 번 전구의 상태를 바꾸는 방법은 번 양초에 토글 의식을 진행하는 방법뿐이다. 예를 들어 4번 전구를 켜는 방법은 5번 양초에 토글 의식을 진행하는 방법밖에 없다. 일 때의 예시를 아래 표에서 직접 보면 짝수 번 전구의 상태를 바꾸는 방법은 한 가지씩만 존재함을 쉽게 확인할 수 있을 것이다.

당신은 모든 전구가 꺼져 있기를 원하므로 홀수 번 양초들에는 토글 의식을 진행해서는 안 된다. 다시 말해 짝수 번째 양초에만 토글 의식을 할 수 있다. 그런데 어차피 짝수 번째 양초에만 토글 의식을 할 수 있다면, 양초를 두 개씩 묶어서 생각하면 사실상 등급 충명을 소환하는 문제를 푸는 것과 같다. 즉, 등급 충명을 소환하는 문제를 푼 다음 모든 양초의 번호에 2배를 하는 합성수 전략을 사용하면 짝수 등급 충명을 소환하는 모든 방법을 확실히 찾을 수 있다.

8등급 충명을 소환하려면 4등급 충명을 소환할 수 있어야 하고, 4등급 충명을 소환하려면 2등급 충명을 소환할 수 있어야 한다. 그러나 우리는 2등급 충명을 소환할 수 없음을 이미 알고 있다. 따라서 8등급 충명은 소환할 수 없다.

–

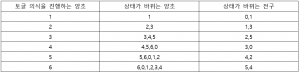
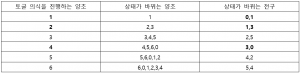
4.19999999는 소수이므로 위에서 말한 합성수 전략을 사용할 수는 없다.이제 홀수 등급 충명을 소환하려 하는 경우를 관찰할 차례다. 예를 들어 7등급 충명을 소환하려 할 때 위와 같이 표를 만들면 다음과 같다.

여기서 재미있는 관찰을 할 수 있는데, (0번 양초를 제외한) 모든 양초에 토글 의식을 진행한다면 모든 전구의 상태가 정확히 2번씩 바뀌어서 도로 꺼진다는 사실이다. 그렇다면 모든 양초에 토글 의식을 진행한 후에는 모든 양초의 상태가 같을 것이다. 즉 모든 양초가 켜져 있거나 모든 양초가 꺼져 있을 것이다. 그렇다면 이 모든 양초 전략을 실행한다고 하면 어떨 때 모든 양초가 켜져 있고, 어떨 때 모든 양초가 꺼져 있을까?

등급의 충명을 소환하려 할 때 모든 양초 전략을 실행한다면 양초의 상태를 총 번 바꾸게 된다.  이므로 양초의 상태를 총 짝수 번 바꾸게 되는 셈이다. 전체 양초가 홀수 개이며 최종적으로 양초의 상태가 모두 같으니 각 양초의 상태를 짝수 번씩 바꾸었다는 이야기가 되고, 모든 양초가 꺼져 있는 상황에 도달한다. 따라서 모든 양초 전략은 등급의 충명을 소환할 때는 사용할 수 없다.

반면 등급의 충명을 소환하려 할 때 모든 양초 전략을 실행한다면 양초의 상태를 총  번 바꾸게 된다.  이므로 양초의 상태를 총 홀수 번 바꾸게 되는 셈이다. 전체 양초가 홀수 개이며 최종적으로 양초의 상태가 모두 같으니 각 양초의 상태를 홀수 번씩 바꾸었다는 이야기가 되고, 모든 양초가 꺼져 있는 상황에 도달한다. 따라서 모든 양초 전략은 등급의 충명을 소환할 때는 항상 사용할 수 있다.

19999999는  꼴의 자연수이므로 모든 양초 전략을 사용할 수 있다. 따라서 1번부터 19999998번까지의 모든 양초에 토글 의식을 진행하면 19999999등급 충명을 소환할 수 있다.

–

보너스. 여기까지 관찰했으면 등급 충명을 소환하는 구체적인 방법을 모두 찾는 체계적인 전략을 구상할 수 있다. 먼저 이 짝수일 때는 등급 충명을 소환하는 문제를 푼 다음 모든 양초의 번호에 2를 곱하는 합성수 전략을 사용하면 된다는 점을 보였다. 이 홀수일 때는 “전구를 모두 끄는 사이클”들을 모두 찾으면 된다. 예를 들어 의 표를 다시 가져오자.

1번 양초에 토글 의식을 진행해서 0번과 1번 전구를 켰다고 하자. 1번 전구를 다시 끄려면 2번 양초에 토글 의식을 진행해야 하고, 그러면 3번 전구가 켜진다. 3번 전구를 다시 끄려면 4번 양초에 토글 의식을 진행해야 하고, 그러면 0번 전구도 꺼진다. 하나의 사이클이 완성되었다. 번 양초에 토글 의식을 진행하면 모든 양초가 켜져 있거나 꺼져 있을 것이다. 켜져 있을지 꺼져 있을지는 양초의 상태를 총 몇 번 바꾸었는지로 찾으면 되는데, 은 홀수이므로 모든 양초가 켜져 있을 것이다. 따라서 번 양초에 토글 의식을 진행하면 7등급 충명을 소환할 수 있다.

반면 3번 양초에 토글 의식을 진행해서 2번과 5번 전구를 켰다고 하자. 5번 전구를 다시 끄려면 6번 양초에 토글 의식을 진행해야 하고, 그러면 4번 전구가 켜진다. 4번 전구를 다시 끄려면 5번 양초에 토글 의식을 진행해야 하고, 그러면 2번 양초도 꺼진다. 하나의 사이클이 완성되었다. 번 양초에 토글 의식을 진행하면 모든 양초가 켜져 있거나 꺼져 있을 텐데, 는 짝수이므로 모든 양초가 꺼져 있을 것이다. 따라서 번 양초에 토글 의식을 진행하는 것은 결과에 영향을 미치지 않는다. 위의 결과와 조합하면 번 양초에 토글 의식을 진행해도 7등급 충명을 소환할 수 있다는 사실을 알 수 있다.

표를 그리지 않고 사이클을 찾으려면 임의의 를 골라 번 양초, 번 양초, 번 양초, 번 양초, … 에 의식을 진행하다가 다시 번 양초로 돌아오는 순간을 찾으면 된다 (mod ). 그 순간이 사이클이 완성된 순간이다. 그런 다음 이 사이클이 모든 양초를 켜는지 끄는지를 판별한다. 이렇게 모든 사이클을 찾은 다음, 양초를 모두 켜는 사이클을 홀수 개, 양초를 모두 끄는 사이클을 아무 개수만큼 골라 조합하면 그것이 홀수 등급 충명을 소환하는 방법이 된다.