기계 학습이 낯선 환경에 적응하는 방법

들어가며

최근 신경망^{neural network}과 같은 복잡한 모델을 활용한 기계 학습은 이미지 인식, 자연어 처리, 음성 인식, 자율주행 등 다양한 응용 분야에서 놀라운 발전을 이루어내고 있습니다. 이러한 기술 발전은 우리가 일상적으로 사용하는 많은 기술과 서비스에 영향을 미치고 있으며 새로운 가능성을 열어주고 있습니다. 그러나 이러한 발전에도 불구하고, 기계 학습 모델들은 주로 훈련 데이터^{training data} 와 유사한 분포를 가진 데이터에 대해서만 높은 성능을 보이는 경향이 있습니다. 즉, 모델이 훈련된 데이터와 실제 적용될 테스트 데이터^{test data} 간에 분포 차이가 존재할 때, 이를 분포 변화 또는 분포 이동^{distribution shift}이라고 하며, 이로 인해 모델의 성능이 크게 저하될 수 있습니다.

분포 변화는 다양한 원인에 의해 발생할 수 있습니다. 예를 들어 자율주행 차량을 생각해봅시다. 차량이 주행하는 지역에 따라 센서에 감지되는 도시의 건물 형태, 거리의 인구 밀도, 교통 표지판의 종류와 배치 등이 달라질 수 있습니다 (그림 1). 또한 시간대에 따라 건물에 비치는 음영과 그림자, 교통량 등이 달라질 수 있습니다. 이러한 요인들로 인해 지역과 시간에 따른 데이터의 분포에 변화가 발생하게 됩니다. 만약 자율주행 기계 학습 모델이 특정 지역의 특정 시간대 데이터로 학습되었다면, 이 모델이 새로운 지역이나 시간대에 적용될 때 환경의 변화에 적응하지 못할 수 있습니다. 이와 같은 분포 변화 문제를 해결하기 위해 도메인 적응^{domain adaptation}에 관한 연구가 활발히 진행되고 있습니다. 도메인 적응은 모델이 학습된 도메인 (소스 도메인source domain)과는 분포가 다른 새로운 도메인 (타겟 도메인target domain)에서도 성능을 유지하도록 하는 통계적 학습 문제이며 이를 해결하기 위해 다양한 방법론이 제안되었습니다. 이 글에서는 도메인 적응에서 주요한 접근법 중 하나인 불변 특징^{invariant feature}을 활용하는 방법론에 대해 설명하고 이러한 방법론들이 여러 종류의 분포 변화 문제를 해결하는데 어떻게 기여하는지 소개하고자 합니다.

신경망과 특징 학습

도메인 적응을 본격적으로 소개하기에 앞서 신경망^{neural network}의 특징 학습^{feature learning, 혹은 표현 학습representation learning}에 대해 간략히 얘기해보겠습니다. 신경망과 기계 학습에 대한 기초적인 틀에 대해 더 깊게 이해하고 싶은 독자는 김동환 교수님의 HORIZON 기사 “최적화와 기계학습”을 먼저 읽으시는 것을 추천드립니다. 기계 학습에서 지도 학습^{supervised learning}은 기계 학습의 한 유형으로, 주어진 입력 데이터input data (혹은 공변량covariate이라고도 불립니다)와 그에 상응하는 레이블^label로 구성된 데이터를 사용하여 새로운 데이터에 대해 정확한 예측을 수행할 수 있는 모델을 학습하는 방법입니다. 수식적으로 표현하면 우선 입력 데이터 \(X\)와 레이블 \(Y\)가 특정한 확률 분포 \((X,Y)\sim P_{X,Y}\) 로 부터 생성되며 이 분포로부터 \(n\)개의 샘플로 이루어진 훈련 데이터셋 \(\{(X_i,Y_i)\}_{i=1}^{n}\)이 주어집니다. 이러한 훈련 데이터셋을 사용하여 예측 모델 \(h\)를 학습하며, 이렇게 학습된 모델이 동일한 분포에서 나온 새로운 테스트 데이터 \((\widetilde{X},\widetilde{Y})\sim P_{X,Y}\)에 대해서도 정확한 예측을 할 수 있도록 하는 것이(즉  \(h(\widetilde{X})\approx \widetilde{Y}\)) 목표입니다.

모델 \(h\)를 학습하는 다양한 통계적 및 기계 학습 방법론이 존재하지만 최근에는 신경망을 활용한 방법이 큰 성공을 거두면서 많은 인기를 끌고 있습니다. 신경망이 중요한 성공을 거둔 이유는 여러 가지가 있겠지만, 그중 하나는 신경망의 뛰어난 특징 학습^{feature learning} 능력입니다. 특징 학습은 지도 학습의 중요한 영역으로, 모델이 입력 데이터에서 레이블 예측에 유용한 특징^feature을 자동적으로 추출하는 과정을 의미합니다. 전통적인 기계 학습에서는 도메인 전문가들이 수작업으로 특징을 정의하고 추출하는 것이 일반적이었습니다. 예를 들어, 이미지 데이터를 분석할 때, 전문가들은 여러가지 기법을 사용하여 이미지의 에지^edge나 모서리^corner 혹은 곡률^curvature과 같은 특징을 수작업으로 추출하였습니다. 이러한 작업은 데이터 특성에 대한 전문적인 이해와 많은 시간을 요구하였습니다.

그러나 신경망은 이러한 특징 추출을 자동으로 학습함으로써, 이 과정을 훨씬 더 효율적으로 만들었습니다. 예를 들어 이미지 데이터 분석에 널리 사용되는 CNN^{convolutional neural network} 모델은 신경망의 여러 층^layer을 통해 입력 이미지로부터 특징을 계층적으로 학습하는 것으로 잘 알려져 있습니다. CNN의 초기 층은 이미지의 경계선이나 모서리와 같은 저레벨^low-level 특징을 학습하고, 더 깊은 층에서는 이러한 저레벨 특징을 조합하여 사람의 얼굴이나 특정 물체의 형태와 같은 고레벨^high-level의 추상적인 특징을 학습합니다. 이러한 계층적 특징 학습 과정을 통해 신경망은 데이터에 적응하여^{data-adaptive} 레이블 예측에 필요한 특징을 스스로 학습하고 이를 통해 여러 분야에서 매우 높은 성능을 발휘하며, 특히 이미지나 텍스트와 같은 복잡한 패턴 인식 작업에서 탁월한 결과를 보여주었습니다.

분포 변화와 허위 상관관계

신경망이 특징 학습을 통해 복잡한 데이터로부터 중요한 특징을 추출하고 이를 바탕으로 높은 성능을 발휘할 수 있다는 점을 앞서 살펴보았습니다. 그러나 신경망과 같은 복잡한 모델을 사용하더라도 훈련 데이터와 테스트 데이터 간에 분포 차이가 있는 경우 성능이 크게 저하될 수 있다는 것이 여러 연구를 통해 경험적으로 입증되었습니다. 그렇다면 분포 변화가 모델의 성능에 어떤 영향을 미치는 것일까요? 이 문제는 흔히 허위 상관관계^{spurious correlation}와 관련이 있습니다. 예를 들어 이미지 분류 모델이 이미지로부터 소^cow를 감지한다고 가정해봅시다. 만약 훈련 데이터에서 대부분의 소 이미지가 목초지를 배경으로 하고 있다면, 모델은 목초지에 관련된 풀, 색깔 등과 같은 특징들을 소의 존재 유무와 강하게 연관짓게 될 것입니다. 결과적으로, 이러한 데이터로 학습된 모델은 소의 형태나 체형과 같은 인과적 특징^{causal feature}보다는 목초지라는 배경에 연관된 특징을 바탕으로 소를 예측할 가능성이 큽니다. 이러한 상황에서 테스트 데이터가 훈련 데이터와는 다른 배경, 예를 들어 해변에서 찍힌 소의 이미지를 포함하고 있다면 모델은 목초지라는 배경의 특징을 더 이상 활용할 수 없기 때문에 소를 정확히 예측하지 못할 상황이 발생 할 수 있습니다. 이와 같은 목초지 배경과 소 사이의 허위 상관관계는 이미지가 생성된 “위치”와 같은 혼란 요인^{confounding factor}으로 인해 훈련 데이터에서는 통계적으로 유의미한 상관관계가 나타나지만 분포 변화가 존재하는 새로운 데이터에서는 존재하지 않을 수 있습니다. 따라서 허위 상관관계에 기반한 예측 모델은 이전에 접하지 않은 새로운 상황에서는 강건성^robustness이 떨어질 수 있습니다.

위와 같은 허위 상관관계에 의존한 예측이 훨씬 더 큰 위험을 초래하는 경우도 쉽게 찾아볼 수 있습니다. DeGrave et al. 논문[1] 에서는 흉부 방사선 사진에서 Covid-19를 예측하는 AI시스템이 Covid-19를 감지할 때 폐의 투명도 변화와 같은 의학적으로 타당한 특징 외에 방사선 사진의 좌우 표시 마커^{laterality markers}나 환자의 자세와 같은 비의학적 요소에 의존한다는 것을 보여주었습니다. 이러한 시스템은 새로운 병원에 적용될 때 실패할 수 있으며, 그 결과 환자의 Covid-19 여부를 잘못 예측하는 상황을 초래할 수 있습니다. 다른 사례로 최근 분포 변화에 대한 알고리즘을 체계적으로 평가하기 위해 WILDS 벤치마크[2]가 도입되었습니다. WILDS는 실제 환경에서 발생하는 다양한 분포 변화를 반영하는 10개의 데이터셋으로 구성되어 있으며 (종양 식별을 위한 병원 간 이동, 야생 동물 모니터링을 위한 카메라 트랩 간 이동, 위성 이미지 및 빈곤 지도 제작에서의 시간 및 위치 간 이동 등) Koh et al.[3]과 Sagawa et al.[4]의 논문에서는 이 데이터셋을 통해 기존의 신경망에 기반한 기계 학습 모델들이 실제 분포 변화에 얼마나 취약한지를 보여주었습니다.

결국 분포 변화가 존재하는 상황에서 허위 상관관계에 의존한 예측 문제는 단순히 모델의 특징 학습 능력이나 성능의 문제라기보다는 분포가 다를 수 있는 다양한 상황에서 데이터를 충분히 관측하지 못한 데서 비롯된 본질적인 한계라고 할 수 있습니다. 도메인 적응에서는 이러한 한계를 극복하기 위해 다양한 데이터셋을 활용하여 분포 변화를 해결할 수 있는 방법론들이 개발되었습니다. 이러한 접근법을 통해 모델이 단일 데이터셋에 존재하는 허위 상관관계에 의존하지 않고 보다 일반화된 특징을 학습하여 실제 상황에서도 일관된 성능을 발휘할 수 있도록 합니다.

불변 특징을 이용한 도메인 적응

우선 도메인 적응의 문제를 다음 용어를 통해 좀 더 구체적으로 설명해보겠습니다. 도메인^domain 또는 환경^environment은 데이터가 수집되는 특정 맥락^context를 의미하며 통계학적으로는 데이터를 생성하는 확률분포와 이로부터 주어진 유한개의 데이터셋^dataset으로 정의할 수 있습니다. 소스 데이터^{source data}는 모델이 훈련되는 학습 데이터셋을 의미하며 특정 소스 도메인에서 수집된 데이터입니다. 타겟 데이터^{target data}는 모델이 실제로 적용될 데이터셋을 의미하며 일반적으로 소스 데이터와 다른 도메인에서 수집된 데이터를 가리킵니다.

도메인 적응에서는 \(E\)개의 서로 다른 소스 데이터 분포 \(P^{(e)}_{X,Y}\), \(e=1,\ldots,E\)로부터 \(n^{(e)}\)개의 입력 데이터 \(X\)와 레이블\(Y\)의 쌍으로 이루어진 소스 데이터 \(\{ (X_i^{(e)}, Y_i^{(e)}) \}_{i=1}^{n^{(e)}} \sim P^{(e)}_{X,Y}\)가 주어집니다. 또한 타겟 데이터 분포 \(P^{(T)}_{X,Y}\)로부터 \(n\)개의 입력 데이터 \(\{ (X_i^{(T)}) \}_{i=1}^{n} \sim P^{(T)}_{X}\)가 주어져 있을 때 (\(P^{(T)}_{X,Y}\)의 \(X\)에 관한 주변marginal 분포), 소스 데이터와 레이블이 없는 타겟 입력 데이터문헌에서는 흔히 unlabeled data라고 부름를 활용하여 타겟 분포에서 관측되지 않은 레이블 \(Y\)을 잘 예측하는 모델을 학습하는 것이 목표입니다. 즉, 타겟 분포에서 새로운 데이터 \((X^{(T)},Y^{(T)})\sim P^{(T)}_{X,Y}\)에 대해 \(h(X^{(T)})\approx Y^{(T)}\)를 만족하는 모델 \(h\)를 학습하는 것입니다. 일반적으로 한 개의 소스 데이터와 레이블이 없는 타겟 데이터를 활용하는 경우 \((E=1)\) 를 단일 소스 도메인 적응^{single-source domain adaptation}이라고 부르며 여러개의 소스 데이터와 레이블이 없는 타겟 데이터를 활용하는 경우 \((E>1)\) 다중 소스 도메인 적응^{multi-source domain adaptation}이라고 합니다. 또한 타겟 데이터에서 레이블이 없는 경우를 비지도 도메인 적응^{unsupervised domain adaptation}이라고도 합니다.

도메인 적응과 밀접하게 관련된 문제로 도메인 일반화^{domain generalization}가 있습니다. 도메인 일반화는 도메인 적응과 달리 타겟이 되는 분포로부터 어떠한 데이터도 관측하지 않고,\(E\)개의 소스 도메인 데이터만을 사용하여 학습된 모델이 아직 관측하지 않은 새로운 타겟 도메인에서도 잘 작동하도록 하는 문제를 의미합니다. 따라서, 도메인 적응과 도메인 일반화의 가장 큰 차이점은 타겟 분포로부터 나온 (레이블이 없는) 데이터를 추가적으로 활용할 수 있는지 여부입니다. 두 문제 모두 타겟 분포에서 레이블을 정확히 예측하는 것을 목표로 하며, 방법론도 유사하기에 이 글에서는 두 문제를 따로 구분하지 않고 논의하겠습니다. 이는 도메인 적응에서 레이블이 없는 타겟 데이터를 활용하지 않으면 그 자체로 도메인 일반화 문제가 되기 때문입니다.

일반적으로 도메인 적응이 성공하려면 소스 분포 \(P^{(e)}_{X,Y}\)와 타겟 분포 \(P^{(T)}_{X,Y}\)간에 레이블 예측에 도움이 되는 연관성이 있어야 합니다. 만약 어떠한 연관성도 존재하지 않는다면 소스 데이터와 레이블이 없는 타겟 데이터만으로는 타겟 레이블을 정확히 예측할 수 있는 모델을 학습하는 것이 불가능하기 때문입니다. 따라서 도메인 간 분포 변화가 어떻게 이루어지는지에 대한 가정에 따라 다양한 이론과 방법론들이 제시되었습니다. 이 글에서는 그 중 흔히 사용되는 방법론인 불변 특징^{invariant feature}을 사용하는 방법론을 소개하겠습니다.

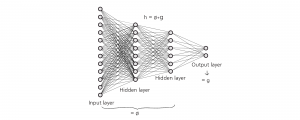
불변 특징을 학습하는 방법론은 다양한 동기에 의해 개발되었으며, 여러 가지 접근법이 존재합니다. 기본적인 접근법은 다음과 같습니다. 신경망과 같은 모델은 복잡한 데이터로부터 예측에 유용한 특징을 효율적으로 학습하며, 이를 통해 레이블을 정확히 예측할 수 있음을 위에서 살펴 보았습니다. 도메인 적응에서 학습하고자 하는 모델 \(h\)을 신경망으로 나타내는 경우, 모델은 입력 데이터 \(X\)로부터 특징을 추출하는 표현 함수\(\phi\)와 이 특징을 기반으로 레이블 \(Y\)를 예측하는 예측기^predictor \(g\)의 두 단계로 나눌 수 있습니다. 이 경우 \(h=g\circ \phi\)로 나타낼 수 있습니다. 표현 함수 \(\phi\)는 데이터로부터 레이블 예측에 필요한 특징들을 학습하며 그 중에는 도메인 간 분포 변화에 따라 레이블과의 상관관계가 변하는 특징과, 도메인이 바뀌어도 레이블과의 관계가 안정적인 불변 특징이 있을 것입니다. 불변 특징을 활용하는 방법론은 \(\phi\)가 불변 특징만을 학습할 수 있도록 하는 것을 목표로 합니다.

이 접근법은 도메인 간 분포 변화가 있어도 공통적인 데이터의 특징들이 존재한다는 가정에 기반합니다. 불변 특징들은 도메인 간 분포 변화에도 불구하고 레이블과의 상관관계가 안정적이기 때문에 이를 기반으로 모델을 학습하면 새로운 타겟 도메인에서도 안정적인 성능을 유지할 수 있습니다. 반면 허위 상관관계를 유발하는 특징들은 도메인에 따라 달라지므로 예측에 사용되지 않습니다. 위에서 보았던 이미지에서 소를 감지하는 문제를 생각해보면 이 접근법은 이미지의 배경에 관련된 허위 상관관계를 유발하는 특징들은 무시하고 소의 형태와 관련된 특징들만을 이용하여 예측 모델을 학습하는 것으로 볼 수 있습니다. 이 경우 배경이 목초지에서 해변으로 바뀌더라도 모델은 여전히 소를 잘 감지할 수 있습니다. 이러한 접근법은 ‘도메인 불변 표현 학습^{domain invariant representation learning}‘이라고도 불리며 분포 변화를 극복하기 위한 대표적인 방법론 중 하나입니다.

마지막으로 소스와 타겟에서 학습된 특징이 유사하다는 제약 조건 \((P^{(1)}_{\phi(X)} \approx P^{(T)}_{\phi(X)})\)이나, 여러 소스 데이터에서 학습된 특징이 레이블을 안정적으로 예측한다는 제약 조건 (즉, 모든 소스 도메인 \(e\)에 대해 \(\phi(X^{(e)})\)와 \(Y^{(e)}\)의 관계가 유사함) 을 통해 최종 모델이 불변 특징만을 학습하도록 유도할 수 있습니다. 이를 통해 불변 특징에 대한 사전 지식 없이도 데이터에 적응적인 방식으로 불변 특징을 학습할 수 있습니다. 물론 이러한 접근법은 다음과 같은 주의점을 내포하고 있습니다. 첫째, 소스와 타겟에서 학습된 특징이 유사하다는 제약 조건 \((P^{(1)}_{\phi(X)} \approx P^{(T)}_{\phi(X)})\)의 경우, 타겟 도메인에서 레이블 \(Y\)를 관측하지 못하기 때문에, 추가적인 가정 없이는 이 조건이 \(\phi(X)\)와 \(Y\)의 관계의 안정성을 보장하지는 않습니다. 둘째, 여러 소스 데이터로부터 \(\phi(X^{(e)})\)와 \(Y^{(e)}\)의 관계가 유사한 특징을 학습하는 경우, 소스 도메인의 개수가 충분하지 않으면, 추가적인 가정 없이는 타겟 도메인에 일어날 수 있는 분포 변화를 포괄하지 못해 소스 도메인으로부터만 학습된 불변 특징이 타겟 도메인에서는 좋은 예측에 실패할 수 있습니다. 궁극적으로 도메인 적응의 성공은 소스 도메인에서 타겟 도메인으로의 분포 변화에 대한 가정과 성공적인 불변 특징 학습을 위해 충분한 수의 소스 도메인을 확보하는 것에 달려있습니다. 아래에서는 이러한 방법론이 개발된 근거에 대한 좀 더 자세한 동기와 알려진 이론적 결과들을 간략히 소개하겠습니다.

일반화 이론에 기반한 도메인 간 분포 매칭

소스 데이터와 레이블이 없는 타겟 데이터를 활용하여 불변 특징을 학습하는 방법론에 대해 먼저 소개하겠습니다. 이 접근법은 분포 간 변화가 존재할 때 모델의 일반화 이론^{generalization theory}을 기반으로 개발된 방법으로 소스와 타겟 도메인에서 학습된 특징이 유사하다는 분포 매칭에 관한 제약조건 \((P^{(1)}_{\phi(X)} \approx P^{(T)}_{\phi(X)})\)을 따르는 표현 함수를 학습하는 것에 중점을 두고 있습니다. 일반화 이론에 기반한 알고리즘을 설명하기에 앞서 도메인 적응에서의 일반화 이론을 간략히 소개하겠습니다. 분포 간 변화가 있을 때 타겟 분포에서 모델의 일반화에 관한 이론은 Ben-David et al.의 논문[5]에서 처음 다루어졌습니다. 일반화 이론은 유한한 데이터로 부터 학습된 모델이 테스트 데이터에 얼마나 정확하게 예측할 수 있는지를 수학적으로 정량화한 이론으로, 기존 학습 이론은 소스와 타겟 분포가 같은 경우, 즉 소스 데이터와 타겟 데이터가 동일한 분포로부터 i.i.d.로 관측되는 경우를 다루었지만 Ben-David et al. 논문에서는 이를 분포가 다른 도메인 적응의 경우로 확장하였습니다.

하나의 소스 분포 (편의상 첫 번째 소스 분포를 다루겠습니다) \(P^{(1)}_{X,Y}\)와 타겟 분포 \(P^{(T)}_{X,Y}\)가 주어졌을 때 \(X\)에서\(Y\)로 매핑하는 모델 \(h\in H\)의 소스 분포와 타겟 분포에서의 위험도^risk를 각각 \(R_S(h)\)와 \(R_T(h)\)로 표기하면 타겟 분포에서의 리스크는 다음과 같이 대략적으로 바운드가 됩니다 (자세한 내용이 궁금한 독자는 Theorem 2 of [5] 참조):

\(R_T(h)\leq R_S(h) + D(P^{(1)}_X, P^{(T)}_X) + \lambda.\)

여기서 \(D\)는 두 분포 \(P^{(1)}_X, P^{(T)}_X\)사이의 거리를 측정하는 거리 함수이고 \(\lambda\)는 모델 클래스 \(H\)가 달성할 수 있는 최적의 소스와 타겟 리스크의 합 \(\lambda = \min_{h\in H}R_S(h)+R_T(h)\)으로 정의됩니다. 모델 클래스 \(H\)가 고정되어 있을 때 소스와 타겟 분포가 유사할수록 \(\lambda\)가 작은 값을 가지므로 \(\lambda\)를 소스 분포에서 타겟 분포로의 적응 가능성으로 해석할 수 있습니다.

이 식을 살펴보면 모델의 타겟 리스크 \(R_T(h)\)를 줄이기 위해서는 그 상한에 해당하는 모델의 소스 리스크 \(R_S(h)\)와 두 분포 \(P^{(1)}_X, P^{(T)}_X\)간의 거리가 작아야 하며, 적응 가능성에 해당하는 항 \(\lambda\) 또한 작아야 합니다. 여기서 주목할 점은 소스 데이터와 레이블이 없는 타겟 데이터로부터 상한의 처음 두 항에 해당하는 소스 리스크 \(R_S(h)\)와 분포 간의 거리 \(D(P^{(1)}_X, P^{(T)}_X)\)는 추정이 가능하다는 것입니다. 이를 기반으로 도메인 적응을 위한 다음과 같은 방법을 생각해볼 수 있습니다.

(1) 신경망 모델 \(h\)를 앞서 살펴보았듯이 특징을 추출하는 표현 함수 \(\phi\)와 레이블 \(Y\)를 예측하는 예측기 \(g\)의 두 단계로 나누어 \(h=g\circ \phi\)로 나타냅니다.
(2) 표현 함수의 공간 위에서 소스 데이터 \(\phi(X^{(1)})\)와 타겟 데이터 \(\phi(X^{(T)})\)의 분포가 유사하여 두 분포롤 통계적으로 구분하기 어렵도록 표현 함수 \(\phi\)를 학습합니다. 이를 통해 \(D(P^{(1)}_{\phi(X)}, P^{(T)}_{\phi(X)})\)를 작게 만들 수 있습니다 (여기서 \(P^{(1)}_{\phi(X)}\)와 \(P^{(T)}_{\phi(X)}\)는 \(\phi(X^{(1)})\)와 \(\phi(X^{(T)})\)의 주변 분포를 의미합니다).
(3) 표현 함수 \(\phi\)가 주어질 때 소스 데이터를 잘 예측할 수 있는 예측기 \(g\)를 학습합니다. 이 단계에서는 소스 데이터의 레이블을 사용하여 \(R_S(h)=R_S(g\circ \phi)\)를 최소화하는 방향으로 \(g\)를 최적화합니다. 학습된 표현 함수 \(\phi\)와 예측기 \(g\)를 결합하여 타겟 데이터에 적용하면 타겟 레이블을 예측할 수 있습니다.

위 방법을 최적화 관점으로 적어보면 다음과 같은 표현 함수 \(\phi\)와 예측기 \(g\)에 관한 최적화 문제로 나타낼 수 있습니다.

\(\min_{\phi,g} R_S(g\circ \phi) \text{ subject to } D(P^{(1)}_{\phi(X)}, P^{(T)}_{\phi(X)})=0.\)

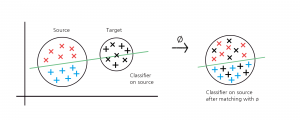
여기서 \(D\)는 두 확률 분포 사이의 거리를 측정하는 함수이며 \(D\)의 선택에 따라 문헌에서 다양한 알고리즘이 제안되었습니다. 대표적으로 Ganin et al.의 논문[6]에서는 \(D\)를  Jensen-Shannon 발산을 사용하고 실제 구현에서는 GAN[7]의 적대적 학습^{adversarial learning} 기법을 사용하여 표현 함수와 예측기를 학습합니다. 이외에도 Wasserstein 거리나 Maximum Mean Discrepancy (MMD)와 같은 다른 분포 간 거리 함수를 이용해 표현 함수와 예측기를 학습할 수 있습니다. 앞서 소개한 Ben-David et al.의 이론적 결과를 바탕으로 이러한 방법론들은 상한의 두 항을 최소화하는 전략으로 이해할 수 있으며 구체적으로는 분포 매칭을 통해 소스와 타겟 도메인 간의 불변 특징을 나타내는 표현 함수를 찾고 \((D(P^{(1)}_{\phi(X)}, P^{(T)}_{\phi(X)})=0)\) 그 공간에서 소스 도메인의 리스크를 최소화하는 \((R_S(g\circ \phi)\) 작게) 예측기를 찾는 것으로 이해할 수 있습니다 (그림 5).

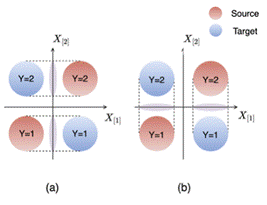
비록 이 접근법을 기반으로 다양한 변형 알고리즘이 제안되었으나, 이러한 알고리즘들이 항상 분포 변화하에서 성공적으로 작동하지는 않습니다. 예를 들어, 소스와 타겟 데이터가 아래 그림 (그림 6)과 같이 주어진 상황에서는 소스와 타겟 도메인 모두에서 \(\phi(X)\)의 분포가 같아지게 하기 위해 (a)와 같이 \(X\)를 \(X_{[2]}\)의 방향으로 사영시키거나 \((\phi(X)=X_{[2]})\) (b)와 같이 \(X_{[1]}\)의 방향으로 사영시키는 방법 \((\phi(X)=X_{[1]})\)이 있습니다. 그러나 (b)와 같은 상황이 발생하는 경우 소스 도메인에서는 정확한 예측이 가능하지만 타겟 도메인에서 레이블이 뒤바뀌어 잘못된 예측을 하게 됩니다. 이 상황은 얼핏 Ben-David et al.의 이론적 결과와 모순되는 것 처럼 보일 수 있습니다. 하지만 이론적 결과에 따르면 모델 \(h=g\circ \phi\)의 타겟 리스크 \(R_T(g\circ \phi)\)는 소스 리스크 \(R_S(g\circ \phi)\)와 두 분포 \(P^{(1)}_{\phi(X)}, P^{(T)}_{\phi(X)}\) 사이의 거리, 그리고 소스 분포의 타겟 분포로의 적응 가능성에 해당하는 항 \(\lambda=\min_{g} R_S(g\circ \phi) + R_T(g\circ\phi)\)의 합에 의해 바운드됩니다. 이 경우 \(\lambda\)는 표현 함수 \(\phi\)에 의존하기 때문에 \(R_S(g\circ \phi)\)와 \((D(P^{(1)}_{\phi(X)}, P^{(T)}_{\phi(X)})\)를 작게 만들더라도 \(\lambda\)가 증가하여 타겟 도메인에서의 성능이 보장되지 않을 수 있습니다. 또한 \(\lambda\)는 타겟 데이터의 레이블에 의존하기 때문에 관측 가능한 데이터만으로는 추정이 불가능하며 따라서 \(\lambda\)를 최소화시키는 표현 함수 \(\phi\)를 찾는 방법도 불가능합니다. 실제로 타겟 레이블을 사용하지 않고 입력 데이터만으로 타겟 레이블을 정확히 예측하는 것은 분포 변화에 대한 강한 가정 없이는 일반적으로 어려운 문제라고 할 수 있습니다.

이 외에도 소스와 타겟 도메인의 레이블 \(Y\)의 분포에 변화가 있는 경우 (즉 \(P^{(1)}_Y\neq P^{(T)}_Y\)) 두 분포 \(P^{(1)}_{\phi(X)}, P^{(T)}_{\phi(X)}\) 간 차이를 작게 만드는 특징을 학습하더라도 타겟 도메인에서의 예측 성능이 좋지 않을 수 있음을 보일 수 있습니다.[8] 도메인 간 분포 매칭을 활용한 방법론 대한 몇몇 이론적인 연구들[9][10][20] 이 제시되었지만 소스와 타겟 데이터의 생성에 강한 조건이 들어가 있어 어떠한 일반적인 조건하에서 성능을 보장할 수 있는지에 대한 체계적인 연구는 여전히 이루어지고 있는 문제입니다.

인과관계에 기반한 불변 특징 학습

앞서 소개한 방법론에서는 하나의 소스 데이터와 레이블이 없는 타겟 데이터를 이용하여 불변 특징을 학습하는 방법을 소개하였으며 이는 여러 개의 소스 도메인과 레이블이 없는 타겟 데이터를 활용하는 방식으로도 쉽게 확장할 수 있습니다. 그러나 소스와 타겟 데이터의 분포에 대한 추가적인 가정 없이는 근본적으로 레이블이 없는 타겟 데이터만으로 불변 특징을 학습하는 것은 위험을 초래할 수 있음을 확인하였습니다 (그림 6 (b)). 그렇다면 소스와 타겟 데이터에 대해 더 강한 가정을 도입하여, 데이터 생성의 인과적인 관점에서 불변 특징을 어떻게 학습할 수 있을까요?

인과적 관점에서는 도메인 간 분포 변화가 존재하더라도 레이블 \(Y\)를 직접적으로 생성하는 인과 변수들과 레이블 간의 인과적 메커니즘은 변하지 않는다는 불변성 가정^{invariance assumption}에 기반합니다.[11] 이러한 인과 관계의 불변성 가정은 직관적이며 많은 경우에 적절한 가정이 될 수 있습니다. 예를 들어 특정 백신이 특정 바이러스에 대한 면역 반응을 유도하는 메커니즘은 인구의 지역, 계절, 혹은 인구밀도에 상관없이 동일하게 유지됩니다. 따라서 백신이 바이러스에 대한 면역 반응을 유도하는 메커니즘을 식별할 수 있다면 지역 혹은 계절에 관계없이 이 메커니즘을 활용하여 효과적인 예측이나 조치를 수행할 수 있습니다. 이번에 소개할 방법론은 데이터를 생성하는 인과 모델을 가정하고, 이 불변성 가정을 바탕으로 인과 변수와 그에 따른 메커니즘을 학습하여 분포 변화를 극복하는 방법입니다. 표현 함수와 예측기를 사용하여 표현하자면 모든 소스 도메인에서 조건부 분포 (메커니즘) \(Y^{(e)}\mid \phi(X^{(e)})\)가 동일한 표현 함수 \(\phi\)를 찾고 학습된 특징 \(\phi(X^{(e)})\)으로 부터 레이블을 잘 예측할 수 있는 예측기를 학습하는 방법으로 이해할 수 있습니다.

인과 추론^{causal inference}에서 대표적으로 사용되는 방법론 중 하나인 구조적 인과 모델^{structural causal model}은 변수들 간의 인과 관계를 명시적으로 모델링하여 변수 간의 인과적 구조를 이해하는 방법입니다. 예를 들어 \(p\)개의 변수를 가진 입력 데이터 \(X=(X_1,\ldots,X_p)\)와 레이블 \(Y\)의 인과 관계를 명시적으로 표현하는 구조 방정식^{structural equation} 모델은 다음과 같이 표현할 수 있습니다.

\(Y\leftarrow f_Y(X_{\text{pa}(Y)}, \epsilon_Y), \;\; X_j \leftarrow f_j(X_{\text{pa}(X_j)}, \epsilon_j).\)

여기서 \(\text{pa}(Y)\)는 \(Y\)의 부모 변수^{parent variables}를 나타냅니다. 즉, \(Y\)는 \(X_{\text{pa}(Y)}\)와 외생 변수^{exogenous variable} \(\epsilon_Y\)에 의해 결정되며 \(X_{\text{pa}(Y)}\) 는 \(Y\)에 직접적으로 인과적 영향을 미치는 입력 변수들을 나타냅니다. 마찬가지로 \(X_j\)는 다른 입력 변수들 \(X_{\text{pa}(X_j)}\)와 외생 변수 \(\epsilon_j\)에 의해 결정됩니다 (위 방정식을 더 일반화하여 \(X_{\text{pa}(X_j)}\)가 \(Y\)를 포함하는 경우도 생각할 수 있습니다) . 각 함수 \(f_Y\)와 \(f_j\)는 특정 변수들이 어떻게 작용하여 다른 변수를 생성하는지를 나타내는 메커니즘 함수입니다.

도메인 간 분포 변화가 존재하는 경우, 이를 구조방정식 모델을 통해 표현하면 다음과 같이 나타낼 수 있습니다.

\(Y^{(e)}\leftarrow f^{(e)}_Y(X^{(e)}_{\text{pa}^{(e)}(Y)}, \epsilon^{(e)}_Y), \;\; X^{(e)}_j \leftarrow f^{(e)}_j(X^{(e)}_{\text{pa}^{(e)}(X_j)}, \epsilon^{(e)}_j).\)

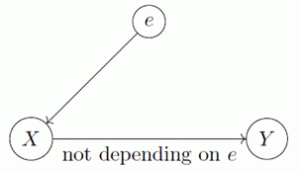
여기서 \(Y^{(e)}, f_Y^{(e)}\)와 같이 도메인 인덱스 \((e)\)에 의존하는 변수들과 메커니즘 함수들은 도메인이 변함에 따라 그 분포나 함수의 형태가 모두 변하는 것으로 이해할 수 있습니다. 인과 관계에 기반한 도메인 적응에서는 앞서 언급한 불변성 가정을 기반으로 하며 이는 위 구조방정식 모델에서 \( f_Y^{(e)}\), \(\text{pa}^{(e)}(Y)\) 그리고 \(\epsilon^{(e)}_Y\)의 분포가 도메인 \(e\)에 관계없이 동일하다는 가정으로 표현할 수 있습니다. 불변성 가정을 인과 그래프^{causal graph}로 표현하면 다음과 같이 나타낼 수 있습니다. (구조적 인과 모델과 인과 그래프에 대해 궁금한 독자는 Pearl 교수님의 “Causality” [12]를 읽어보길 추천드립니다.)

따라서 불변성 가정하에서는 레이블 \(Y\)에 직접적인 영향을 주는 인과 변수  \(X_{\text{pa}(Y)}\)와 메커니즘 함수  \(f_Y^{(e)}=f_Y\)를 찾을 수 있다면 새로운 타겟 분포 \(e=T\)가 주어지더라도 안정적인 예측이 가능합니다. 이는 인과 추론이 견고한 예측을 하는 데 중요한 이유 중 하나로 여겨집니다. 그러나 인과 추론에서 인과 변수에 대한 식별 가능성^{identifiability}은 매우 어려운 문제이며 일반적으로 데이터에 대한 강한 가정 없이는 성립하지 않습니다. 놀랍게도 Peters et al.의 논문[13]에서는 외생 변수들이 정규분포를 따를 때 선형적 구조 방정식 (즉 메커니즘 함수들이 선형인 경우) 하에서 불변성 가정이 성립한다면 충분한 수의 소스 도메인을 관찰할 경우, 조건부 분포 \(Y\mid X_S\)가 불변적 특성을 만족하는 변수들  \(X_S\)이  \(Y\)에 대한 인과 변수라는 것, 즉 \(S=\text{pa}(Y)\)을 증명하였습니다 (이 외에도 논문에서는 인과 변수들의 부분적인 식별 가능성 등 다양한 결과를 증명하였습니다). 인과 변수들이 선형적 구조 방정식 모델 하에서 불변성을 가진다면 이 불변성을 이용해 역으로 인과 변수들을 식별할 수 있다는 결과를 보여준 것입니다.

도메인 간 분포의 이질성^heterogenity으로부터 불변성을 이용해 인과 변수 또는 불변 특징을 학습하는 아이디어는 기계 학습 분야에서 빠르게 적용되고 발전하였습니다. 이러한 아이디어를 대표하는 방법론으로 Arjovsky et al.의 눈문[14]에서 제안한 Invariant Risk Minimization (IRM)을 간략히 소개하겠습니다. IRM은 다음 최적화 문제를 푸는 표현 함수  \(\phi\)와 선형 레이블 예측기 \(w\)를 찾습니다 (IRM에서는 예측기 \(w=g\)를 항상 선형으로 가정하고 있습니다).

 \(\min_{\phi,w} \sum_{e} R_S^{(e)}(w\circ \phi) \text{ subject to } w \in argmin_{\bar{w}} R_S^{(e)}(\bar{w}\circ \phi) \text{ for all \(e\)}.\)

최적화 식을 살펴보면 모든 소스 도메인에서 소스 리스크를 최적화 시키는 예측기  \( w\)가 동일하게 나타나는 표현 함수  \(\phi\)를 찾는 것을 볼 수 있습니다. 회귀나 분류 문제의 경우 특징 공간 위에서 최적의 예측기는 조건부 평균 \(E[Y\mid \phi(X)]\)로 주어지므로 IRM의 제약 조건은 조건부 분포의 평균  \(E[Y^{(e)}\mid \phi(X^{(e)})]\)이 도메인에 관계없이 불변이라는 조건과 동치가 되며 이는 조건부 분포 \(Y^{(e)}\mid \phi(X^{(e)})\)가 불변이라는 제약 조건을 완화시킨 것으로 간주할 수 있습니다. 따라서 IRM을 활용하여 주어진 여러개의 소스 도메인으로부터 조건부 분포 \(Y\mid \phi(X)\)가 불변인 표현 함수를 찾음으로써 타겟 도메인에서도 \(\phi(X)\)에 기반한 예측이 안정적으로 이루어질 수 있습니다.

반인과적 예측 문제와 인과적 표현 학습을 통한 식별가능성

위에서 보았던 입력 데이터 \(X\)가 인과적 메커니즘을 통해  \(Y\)를 생성하는 인과 모델과 달리 반인과적 예측^{anticausal prediction} 문제에서는 레이블 \(Y\)가 입력 데이터  \(X\)를 인과적으로 생성합니다. 그리고 예측 모델은 이러한 데이터 생성 방향과 반대로 \(X\)를 기반으로 \(Y\)를 예측합니다.[15] 따라서 데이터 생성의 인과 관계와 반대 방향으로 예측이 이루어지며 구조 방정식의 관점에서 인과 변수들의 집합인 \(\text{pa}(Y)\)가 공집합이 되는 것을 볼 수 있습니다. 이러한 데이터 생성 모델에서는 레이블이 주어졌을 때 조건부 분포가 불변인 불변 특징이 존재한다는 가정이 흔히 이루어집니다. 흉부 방사선 사진으로부터 Covid-19를 예측하는 이전 예시를 생각해보면 환자의 Covid-19 감염 여부가 주어졌을 때 사진에서 폐 부분의 특징은 어떤 병원(도메인)에서든 동일할 것입니다. 이는 Covid-19에 감염된 환자의 폐 사진에서 관찰되는 특징적 징후들이 의학적으로 동일한 인과관계를 갖기 때문입니다. 반인과적 예측 문제에서 조건부 분포가 불변인 특징을 조건부 불변 특징^{conditionally invariant features}이라고 하며, 조건부 불변 특징이 존재한다는 가정하에 다음과 같은 최적화 문제를 생각해볼 수 있습니다.[16] [17]

 \(\min_{\phi,g} \sum_{e} R_S^{(e)}(g\circ \phi) \text{ subject to } D(P^{(e)}_{\phi(X)\mid Y}, P^{(e’)}_{\phi(X)\mid Y})=0 \text{ for all \(e\neq e’\)}.\)

이 접근법은 앞서 소개한 방법론들과 다르게 레이블이 주어졌을 때 모든 소스 도메인 간의 조건부 분포가 동일하게 되는 표현 함수를 찾음으로써 새로운 타겟 도메인에서도 예측을 성공적으로 수행하는 알고리즘입니다.

지금까지 불변 특징을 학습하기 위한 여러가지 방법론, 즉 일반화 이론에 기반한 소스와 타겟 도메인 간 분포 매칭, 그리고 구조적 인과 모델 혹은 반인과적 예측 문제에 기반한 불변 특징 학습 방법을 살펴보았습니다. 소개한 세가지 접근법들을 요약적으로 나타내면 다음과 같습니다.

(1) 일반화 이론에 기반한 분포 매칭: \(P^{(1)}_{\phi(X)} \approx P^{(T)}_{\phi(X)}\)가 성립하는 표현 함수 \(\phi\)를 찾고  \(\phi\)로 표현되는 특징을 사용해 소스 리스크 \(R_S^{(1)}(g\circ \phi)\)를 최적화하는 예측기  \(g\)를 학습.
(2) 구조적 인과 모델에 기반한 불변 특징 학습: 모든 소스 도메인 \(e, e’\)에 대해 \(P^{(e)}_{Y \mid \phi(X)}\approx P^{(e’)}_{Y \mid \phi(X)}\)인 표현 함수  \(\phi\)를 찾고 \(\phi\)로 표현되는 특징을 사용해 소스 리스크 \(\sum_{e} R_S^{(e)}(g\circ \phi) \)를 최적화하는 예측기  \(g\)를 학습.
(3) 반인과적 예측 문제에서 조건부 불변 특징에 기반한 방법: 모든 소스 도메인 \(e, e’\)에 대해 \(P^{(e)}_{\phi(X)\mid Y} \approx P^{(e’)}_{\phi(X)\mid Y}\)인 표현 함수 \(\phi\)를 찾고 \(\phi\)로 표현되는 특징을 사용해 소스 리스크  \(\sum_{e} R_S^{(e)}(g\circ \phi)\)를 최적화하는 예측기 \(g\)를 학습.

첫 번째 방법론은 일반화 이론을 바탕으로 소스와 타겟 데이터의 분포를 직접적으로 매칭하여 도메인 적응을 수행하는 반면, 두 번째와 세 번째 방법론은 인과적 혹은 반인과적 데이터 생성 모델을 기반으로 학습된 특징이 모든 소스 도메인에서 레이블을 안정적으로 예측하도록 하는 제약 조건을 통해 도메인 적응을 수행합니다. 또한 두 번째와 세 번째 방법론은 첫 번째 방법과 달리 타겟 데이터를 사용하지 않고 여러 소스 도메인으로부터만 불변 특징을 학습합니다. 이는 다양한 분포 변화로 부터 나온 소스 데이터들을 활용하여 불변 특징을 더 안정적으로 학습할 수 있는 장점이 있습니다. 그러나 이 접근법은 많은 소스 도메인으로부터 불변 특징을 학습하기 때문에 첫 번째 방법론과 같이 소스 데이터를 타겟 데이터에 직접 매칭하여 불변 특징을 학습하는 방법에 비해 데이터의 많은 정보를 버리게 됩니다. 이로 인해 타겟 도메인에서 안정적인 성공을 거두더라도 예측 성능이 비교적 떨어질 수 있는 단점이 있습니다. 또한 데이터 생성 모델에 따라 각기 다른 알고리즘이 적용되는 점도 중요한 고려 사항입니다. 따라서 데이터 생성에 대한 사전적인 지식이나 도메인에 대한 이해를 바탕으로 최적의 알고리즘을 선택하고 적용하는 것이 중요합니다. 알고리즘의 결과로 얻어진 특징들을 맹목적으로 신뢰하기 보다는 도메인 지식을 활용하여 면밀히 검토하는 과정이 필요합니다.

마지막으로 중요한 질문이 남아 있습니다. 실제 불변 특징을 학습하기 위해서는 분포가 서로 다른 유한개의 소스 도메인으로부터 생성된 (그리고 타겟 도메인으로부터 생성된 레이블이 없는) 데이터만을 이용해야 합니다. 그렇다면 앞서 소개한 방법들이 유한개의 다른 소스 도메인으로부터 우리가 원하는 타겟 도메인에도 일반화가 가능한 불변 특징을 실제로 학습할 수 있을까요? 위에서 보았듯 분포 변화가 존재하는 경우 구조방정식 모델을 통해 데이터의 생성 과정을 나타낼 수 있었습니다. 구조방정식 모델에서 메커니즘 함수 \(f^{(e)}\)들이 모두 선형 함수인 경우 분포 변화가 일어나는 변동^perturbation방향의 공간의 차원을 \(p\)라고 했을 때 (예컨대 반인과적 모델의 경우 모든 도메인  \(e\)에 대해 \(f^{(e)}(y) – f^{(1)}(y)\)가 \(p\)차원의 부분 공간에 놓여있는 것으로 해석할 수 있습니다), 표현 함수 \(\phi\)가 선형 함수로 제한 된 경우에는 이론적으로 불변 특징을 학습하기 위해서 \(E=O(p)\)만큼의 소스 도메인을 관측해야함을 보일 수 있습니다.[9] [18] [19] 즉 변동이 일어나는 모든 방향으로 소스 도메인을 관측할 수 있다면 변동이 일어나는 방향에 수직인 방향으로 데이터를 사영시켜 불변 특징을 식별할 수 있습니다 (이론적 결과에 대해 궁금한 독자는 [9],[18],[19] 논문을 읽어보는 것을 권해드립니다). 그러나 변동이 좀 더 복잡한 형태를 띄거나 표현 함수가 더 복잡한 함수로 매개화된다면 앞서 소개한 방법들이 어떤 조건에서 타겟 도메인에 불변인 특징을 학습할 수 있는지는 아직 이론적으로 알려져 있지 않습니다.

식별 가능성을 보일 수 있는 도메인 적응 방법론으로 생성적 접근법^{generative approach}를 활용하는 알고리즘도 제시되었습니다. 이러한 방법은 인과적 표현 학습^{causal representation learning}의 식별 가능성을 활용하여 불변 특징을 학습합니다. 인과적 표현 학습은 데이터에 내재된 모든 잠재 변수^{latent variable}를 올바르게 학습하여 인과 구조를 복원하는 것을 목표로 합니다. 어떤 함수 \(f\)가 주어져 있고 데이터가 잠재 변수 \(Z\)에 의해  \(X=f(Z)\)의 생성 과정을 통해 생성되었을 때, 함수 \(f\)나 잠재 변수의 분포에 대한 가정 (예: 함수 \(f\)가 다항식 혹은 부드러운 비선형 함수 / 잠재 변수가 정규성을 가진 선형 구조적 인과 모델을 따름) 그리고 충분한 개수의 개입^{interventions}이 이루어진 소스 도메인을 관측된다면 (예: 각 잠재 변수마다 개입이 일어난 데이터 \(X^{(e)}=f(Z^{(e)})\)) 이러한 가정 하에서 모든 잠재 변수를 특정한 불확정성 (예: 아핀 변환^{affine transformation}) 하에 식별하는 것이 가능하다는 것이 알려져 있는 결과들입니다.[21] [22] [23] 도메인 적응에서는 각각의 도메인을 하나의 개입 데이터에 대응된다고 볼 수 있으며 잠재 변수 \(Z^{(e)}\)가 도메인에 불변인 특징 \(Z_C^{(e)}\)와 도메인에 따라 달라지는 특징 \(Z_S^{(e)}\)로 나눠진다면, 학습된 잠재 변수로부터 불변인 특징 \(Z_C^{(e)}\)만을 활용하여 도메인의 변화에 안정적인 모델을 학습할 수 있습니다.[24] [25] 이러한 인과적 표현 학습을 위해서는 주로 생성 모델^{generative model}을 이용하여 데이터의 잠재 변수를 학습하는 방법이 활용되고 있습니다. (생성 모델에 대한 자세한 설명은 임성빈 교수님의 HORIZON기사 “확률편미분방정식과 인공지능“을 읽어보시길 권해드립니다). 크게 보았을 때 앞서 설명한 방법론들과 생성 모델을 활용한 방법론은 기계 학습에서 차별적 접근법^{discriminative approach}과 생성적 접근법^{generative approach}의 차이로 볼 수 있습니다.

글을 마치며

도메인 적응에 관하여 이 글에서는 불변 특징을 활용한 방법론을 소개하였습니다. 도메인 적응은 아주 광범위한 연구 분야로 제가 소개해 드린 내용은 다양한 방법론 중 극히 일부에 불과하며, 이 외에도 여러가지 상황에서 분포 변화를 극복하기 위한 많은 알고리즘이 제안되었습니다. 예를 들어, 공변량 변화^{covariate shift} 그리고 레이블 변화^{label shift}에서는 각각 \(Y\mid X\)와 \(X\mid Y\)의 분포가 불변이라는 가정하에 적절한 가중치를 추정하는 방법론이 이용되고 있습니다. 또한 도메인 간 리스크의 불변성이나 리스크의 경사에 대한 불변성을 활용하는 알고리즘도 제시되었습니다. 관측한 각 소스 도메인의 최대 리스크를 최소화하는 그룹 분포적으로 견고한 최적화^groupDRO, 학습된 모델로부터 유사^pseudo 타겟 레이블을 생성하여 모델을 업데이트 하는 자기 학습^{self-training} 기법, 데이터 증강^{data augmentation}을 통해 학습된 특징의 견고성을 향상시키는 알고리즘도 많은 연구가 이루어지고 있습니다. 이 외에도 분포 변화와 도메인 적응은 기계 학습의 여러 다른 분야와도 크게 연관되어 있습니다.

현재 도메인 적응에 관한 연구는 주로 모델의 디자인이나 구조를 향상시켜 모델의 성능을 높이는 방향으로 진행되고 있으며 매우 빠르게 발전하고 있습니다. 하지만 앞서 소개한 여러가지 도메인 적응 알고리즘이 성공적인 불변 특징을 배우기 위해 데이터 생성과 알고리즘에 어떤 제약 조건이 필요한지 등 이론적인 부분에 있어서 아직 이해도가 부족하며 해결해야 할 문제들도 많이 있습니다. 이 글을 통해 독자 여러분이 분포 변화에 대응할 수 있는 기계 학습 알고리즘의 중요성과 필요성을 이해하는데 조금이라도 도움이 되기를 바랍니다.