물리 기반 신경망은 전통적 수치해석을 대체할 수 있을까? [2] 한계와 보완 방안

PINN의 한계

우리는 지난 1부에서 PINN의 원리와 기존의 수치해석을 대체할 수도 있을 수준의 장점이 어떤 것이있는지 알아보았다. PINN은 그 원리 상 미분방정식 등의 지배방정식과 경계 조건이 확실한 모델로 자리잡은 문제에 대해서라면 원리적으로는 광범위하게 적용 가능하다. 문제는 물리학이나 공학, 응용 과학 시스템에서 다루는 지배방정식 중에는 늘 이렇게 이른바 잘 설정된 PDE^{well-posed PDE}만 있는 것은 아니라는 것이다. 예를 들어, 초기값이 아니라 최종값이 주어졌을 때 초기값이 어떠했는지를 역으로 추정하는 문제를 생각해 보자. 열방정식을 예로 든다면 시간이 꽤 지난 후 쇠막대의 중간 지점에서의 온도를 알고 있다고 하자. 그렇다면 시간을 앞으로 돌려 초기에 이 쇠막대의 끝부분 온도가 얼마였는지 계산할 수 있느냐는 것이다. FDM, FEM 같은 전통적인 수치해석 방법에서는 이른바 슈팅 알고리즘^{shooting algorithm}을 사용하여 이러한 역문제^{inverse problem}를 푼다. 이 경우, 일단 대략적인 초기값을 추측한 후, 유한 차분 행렬 계산을 반복하여 최종값을 구한 후, 그 값이 이미 알고 있는 최종값과 얼마나 비슷한지 비교해보면서 초기값이 있을만한 범위를 좁혀 나가 결국 충분히 좁은 범위 내의 후보값을 초기값으로 정하는 방식이다. 그렇지만 이러한 역문제는 최종값에 약간 변동이 생길 경우, 초기값의 변동폭, 즉, 불확실성은 더 증폭된다는 문제점이 있다. 언뜻 생각하면 유한차분법에서는 초기값으로부터 시간을 쪼개면서 조금씩 진행시키면서 앞으로 나아가 나중에 시간이 흐른 후의 값을 계산할 수 있으니, 이번에는 최종값이 주어졌을 때 시계를 뒤로 돌리듯 뒤로 시간의 백스텝을 밟아 나가면서 초기값으로 당도하면 되는 것 아닌가 하는 의문을 품을 수 있다. 그런데 사실 이러한 되감기 방식이 유한차분법에서 불완전한 이유는 전통적인 수치해석은 애초부터 연속 시공간을 이산 공간으로 나누어 점프해 가면서 업데이트하는 방식이기 때문에 오차가 항상 발생한다는 것 때문이다. 특히, 그 오차는 시간이 지날수록 누적된다는 것이 문제다. 따라서 오차 허용 한도 이내에서 초기값으로부터 유한 차분 연산을 하면서 최종값으로 도달한 상태는 이미 오차가 확장되는 것을 통제하면서 얻은 값이지만, 최종값에서 역으로 유한 차분 연산을 하면서 초기값으로 도달하는 것은 계산 과정에서 오차가 확장되며 증폭되는 것을 통제할 방법이 마땅치 않다.

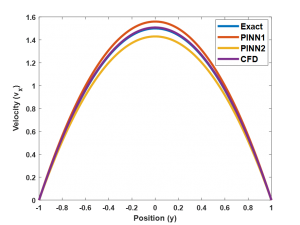
또한 유체의 물리적 흐름을 지배하는 수학적 원리를 정리한 네이비어-스토크스^{Navier-Stokes} 방정식처럼, 대류^convection의 특성을 설명하는 비선형항으로서의 관성항^{inertia term}이 포함된, 그리고 이론적으로는 유일해가 존재하는지조차 증명되지 않은 PDE의 경우에는 오히려 FEM 같은 전통적인 수치해석 기반 유동 계산 방법론인 CFD^{computational fluid mechanics}보다도 더 정확도가 떨어지는 결과가 나올 수도 있다. 예를 들어 그림 4에는 2차원 네이비어-스토크스 방정식 중에서 가장 간단한 경우인 층류^{laminar flow}가 나오는 포아젤 유동^{Poiseuille flow}의 경우를 계산한 결과를 보이고 있다. 이 경우는 해석적 해를 계산할 수 있으므로 CFD와 PINN에서 얻은 결과를 보다 면밀하게 비교 분석할 수 있다. 그림 4에 보였다시피, 충분히 메쉬가 작은 CFD의 경우 해석적 해와 거의 일치하는 결과를 보인 데 반해, ADAM^{Adaptive Moment Estimation}이나 L-BGFS 기반으로 작동하는 PINN에서 얻은 해는 해석적 해와 다소 차이가 나는 결과를 보임을 확인할 수 있다. 특히 유체의 흐름이 더욱 복잡해지는 난류^turbulence 영역에서는 이러한 경향이 확연하다. 난류는 유체 중에서도 레이놀즈 수^{Reynolds number}[1]가 매우 큰 유체가 보이는 예측 불가능한 3차원 유동 현상이다. 주로 가볍고 빠르게 흐르는 공기 같은 유체에서 자주 관측된다. 난류에 대해 지난 100년 넘는 세월 동안 수학, 물리학, 공학 분야에서 수많은 연구가 진행되고 있음에도 불구하고, 난류는 여전히 현재 고성능 슈퍼컴퓨터와 최신 CFD 알고리즘을 활용해도 충분한 정확도로 그 동역학적 특성을 다 설명하지 못 하는 미지의 영역 중 하나이다. 난류에는 해석적 해도 존재하지 않으며, 전통적인 수치해석적 방법에 기반을 둔 CFD로 얻은 해도 유체 흐름의 초기에만 어느 정도 안정적인 범위 내의 오차를 보일 뿐이다. 난류의 특징 중 하나는 시간이 지날수록 난류의 흐름이 더욱 예측 불가능한 영역으로 진입한다는 것, 즉, 확률론적 모형을 따르는 현상을 보인다는 것인데, 이는 수치해석 관점에서는 시간에 따른 오차가 더욱 증폭되는 구조적 특징이 이미 방정식에 내재되어 있음을 의미한다. 난류 문제를 PINN으로 접근할 경우 일단 기본적으로 학습에 활용할 해석적 해가 없는 것, 그리고 참고할 수 있는 수치해석 해조차 초기에만, 그리고 작은 영역 스케일에서만 유효하다는 것, 작은 영역이라고 하더라도 복잡한 형태의 공간에서는 경계조건의 복잡함으로 인하 추가적인 오차 누적이 발생한다는 점 등이 PINN에게는 더욱 불리한 요소로 작용한다.

PINN은 FEM을 이길 수 있는가?

최근 Grossmann, Komorowska, Latz, Schonlieb 등이 arxiv에 공유한 연구 논문[2] 에서는 다양한 물리, 공학 분야에서 활용되는 PDE에 대해 계산 성능, 오차, 신뢰도 등을 종합적으로 비교 분석한 연구 결과가 공개되었다. 저자들이 종합적으로 내린 결론은 지금까지 알아본 결과와 크게 다르지 않다. 일단 PINN은 계산 성능 면에서도 FEM에 비해 유리한 부분이 거의 없었다. 이는 PINN 기반 계산에 걸리는 시간과 에너지를 종합적으로 비교해 봐도 알 수 있는 부분이다. 즉, PINN은 같은 시간 동안 연산하였을 때, FEM보다 수치 해석 오류가 더 컸으며, 비슷한 수준의 수치 해석 오류에 수렴하기 위해서는 훨씬 더 오랜 연산 시간이 필요하거나, 아예 그러한 수준으로의 수렴되는지 여부가 불분명하였다. 또한 PINN은 일부 복소함수 기반의 PDE에 대해서는, 물리 법칙에 기반을 두고 있음에도 불구하고, 아이러니컬하게도 물리적적으로 말이 안 되는 오류를 만들어내기도 하였다. 예를 들어 슈뢰딩거 방정식^{Schrödinger equation}에서는 복소함수 형태의 파동함수가 시공간에서 분포하는 형태를 계산해야 하는데, PINN 기반으로 연산한 결과는 파동함수 고유의 특성, 예를 들어 경계에서의 반사와 간섭 등의 특징이 제대로 구현되지 못함을 보였다. 이는 FEM에서 구현된 결과와 대조되는 것으로, PINN이 복잡한 혹은 복소함수 기반의 PDE에 대해서는 물리적으로 오류를 갖는 해를 만들 수도 있음을 의미하는 것이다. 다만 PINN은 고차원에서 FEM에 대해 상대적인 경쟁력을 보였는데 (예를 들어 3차원 푸아송 방정식 등), 이는 PINN 기반 접근은 다루고자 하는 물리적 현상이나 시스템의 차원이 커질수록 더욱 유리해질 수도 있음을 의미한다. 이는 PINN의 원리를 생각해 보면 당연한 것인지도 모른다. 왜냐하면 PINN은 기본적으로 전통적인 FEM이나 FDM과는 달리, 제한된 도메인 내에서의 메쉬 배치에 의존하지 않기 때문이다. 사실 이러한 메쉬 배치에 의존하는 전통적인 FDM, FEM의 경우, 이른바 차원의 저주^{curse of dimension}에서 자유롭지 못 하다. 예를 들어 가로, 세로 각각 1m인 2차원 평면 위에 간격 1cm로 메쉬를 만든다고 생각해 보자. 그렇다면 메쉬는 총 10,000개 나올 것이며, 경계까지 포함하면 격자점은 총 10,201개 나올 것이다. 그렇지만, 가로, 세로, 높이 각 1m인 3차원 공간 안에 똑같이 간격 1cm로 메쉬를 만든다면, 이제 메쉬는 총 1,000,000개나 나올 것이며, 경계까지 포함하면 격자점은 총 1,030,301개나 나올 것이다. 만약 3차원이 아니라 4차원 공간을 상정한다면 이보다 다시 100배씩 증가한 메쉬와 격자점이 생성될 것이다. 늘어난 격자점과 메쉬는 정확히 그에 비례하는 연산량의 증가를 의미한다. 즉, 위에서 알아본 사례에서 2차원 평면보다 3차원 공간에서 FEM 혹은 FDM 기반으로 PDE를 계산하기 위해서는 100배 연산 시간이 더 걸린다. 이는 반드시 3차원 공간에서 해석해야 하는 난류 같은 유체 문제에 대한 FEM 기반의 시뮬레이션이 매우 비싼 연산이 될 수 밖에 없는 근본적인 원인이 되기도 한다. 난류를 모사하기 위해서는 훨씬 작은 크기의 메쉬가 필요하고, 시간 역시 훨씬 짧은 시간 단위로 설정되어야 하기 때문이다. 또한, 전통적인 FDM에서는 유한 차분을 위한 시간과 공간의 단위 역시 독립적으로 설정될 수 없다. 예를 들어 유한차분법으로 열방정식 같은 확산 방정식을 계산할 경우, 시간과 공간의 차분을 설정하기 위해서는 쿠란트-프리드리히-레위^{Courant-Friedrich-Lewy} 조건을 고려해야 한다. 이에 따르면 시간 차분 은 공간 차분 와 확산 계수^{diffusion coefficient} 에 대해 다음과 같은 제한 조건을 따라야 한다. 

이 조건에 따르면 예를 들어, 공간의 메쉬 간격을 1 μm로 설정했을 때 (즉, ), 확산 계수가 로 주어져 있다면, 시간 차분은 최대 를 넘을 수 없다. 만약 이 시스템에서 일어나는 일이 적어도 1분 정도의 시간 스케일과 1 mm³ 크기의 3차원 공간에서 발생하고 있다면, 이 시스템에서 일어나는 시공간 동역학 특성을 FDM으로 모사하기 위해서는 적어도 600만 번의 시간 단위가 필요한 셈이고, 매 연산은 10억 개의 격자점에서 이루어져야 하므로, 실로 압도적인 연산량을 필요로 하게 된다. 한 시간 단위 (즉, 을 한 단위로 하는 한 번의 iteration)에 현재 필자의 2.5 GHz octa core CPU가 탑재된 랩탑으로 연산해도 1분 남짓의 시간이 걸리는데, 이는 환산하면 이러한 계산에는 보통의 랩탑으로는 10년 넘는 시간이 소요됨을 의미한다. 물론 대부분 이 정도 수준의 연산은 일반적인 랩탑으로는 하지 않고, 병렬 CPU 클러스터 등을 이용하여 수행한다. 그러나 PINN은 FDM, FEM과는 달리 시간과 공간의 차분에 대해 제약 조건이 약하고, 위에서 알아본 차원의 저주로부터 상대적으로 자유롭다. 랜덤하게 선택된 경계 혹은 내부의 collocation point 데이터를 통해 학습을 하며, 학습된 결과는 차원과 상관없이 NN의 은닉층과 각 층에 속한 node에서 최종적으로 업데이트 되기 때문에, 딱히 고차원으로 시스템이 확장된다고 해서 더 많은 연산 부담이 가해지는 것은 아니다. (물론 고차원이 될수록 랜덤하게 선택해야 하는 collocation point 개수는 그만큼 더 증가될 필요는 있지만, 그것이 FEM이나 FDM 같은 전통적인 수치해석 방법에서 요구되는 (즉, 일정한 밀도를 만족시켜야 하는) 지수함수적인 증가는 아니다.) 이러한 장점은 해석적 해가 주어져 있거나, 학습할 데이터 (예를 들어 실험이나 이미지 데이터 등)가 충분히 많이 주어진 경우라면 PINN에게 큰 장점이 된다. 일부 예외적 경우를 제외한다면, 우리가 살고 있는 세상은 대부분 3차원 시스템 안에서 구현되어야 하고, 따라서 차원의 저주에서 자유롭지는 않기 때문이다.

차원의 저주에서는 비교적 안전할지는 몰라도, 아직까지 잘 해결되지 않고 있는 PINN의 문제는 몇 개 더 있다. 일단 다름 아닌 손실 함수의 최적화 과정에서 생기는 문제가 있다. 앞서 살펴본 것처럼, PINN의 손실 함수는 크게 데이터 학습과 PDE 학습에서 비롯되는 함수로 구분된다. 각 학습에서 생기는 오차에 대한 가중치를 어떻게 정해야 하는지에 대해 아직 명확한 이론적 근거는 없다. 다만, 앞서 열방정식 사례에서 알아보았듯, 여러 잘 알려진 PDE에 대해 실험한 결과들은 공통적으로 PDE 학습에 대한 손실 함수의 가중치를 높일수록 학습 속도가 빨라지는 대신, 오차도 같이 커지는 현상이 관측됨을 보고한다. 즉, 물리 법칙에서 벗어나지 못 하게 만드는 구속력이 더 강해질수록 오히려 오차는 더 커지는 바람직하지 못 한 경우가 생길 수 있다는 것이다. 이는 주로 유체와 열에너지의 분포를 동시에 설명하는 이류^advection 현상을 기술하는 PDE나 화학반응-확산^{reaction-diffusion}이 동시에 일하는 시스템을 기술하는 피셔 방정식^{Fisher equation} 등의 PINN 계산 과정에서 관찰된다.[3]  이러한 방정식들의 공통점은 PDE 학습의 손실 함수가 볼록하지 않을 수 있다^non-convex는 점이다. 다른 문제는 데이터 포인트의 배치, 즉, collocation 문제다. 앞서 언급했듯, 랜덤한 collocation points 샘플링은 PINN의 고유한 장점이 될 수 있지만, 이들의 분포 방식에 따라 PINN에서 계산된 해의 변동성이 커질 수 있다는 점은 동시에 고유한 단점이 될 수 있다. 전형적인 PINN은 랜덤하게 분포된 데이터 포인트를 기반으로 하지만, 어떤 PDE는 경계 근처에 혹은 경계에서 먼 쪽에 더 많은 collocation point를 배치하는 것이 더 정확한 해를 얻게 만드는 경우가 있다. 문제는 어떤 경우에 대해 어떤 데이터 분포 양식을 취해야 할지에 대한 명확한 가이드라인이 되어줄 이론적 모델이 없다는 것이다. 즉, 특정한 PDE로 기술되는 시스템의 개략적인 해의 형태 (해의 분포)에 대한 힌트가 충분히 주어져 있지 않다면, 전형적인 랜덤 collocation point로 시작해야 할 수밖에 없다. 그러나 그 collocation point 분포 자체를 학습하기 위한 손실 함수를 정의하기 어렵다는 것은 PINN을 다른 전통적인 격자 기반 수치해석 방법을 대체할 수 있는 방법론으로 우선적으로 선택하는 것을 이끌어내지는 못 한다.[4]

PINN과 전통적인 수치해석의 동행

결국 PINN이 앞으로 전통적인 미분방정식 수치해석 방법인 FEM이나 FDM을 완전히 대체할 것이냐는 질문은 다른 질문으로 재구성될 필요가 있다. PINN은 PINN대로 최적화 알고리즘의 발전, GPU 성능의 발전을 통한 학습 시간의 단축 등의 장점과 기존의 전통적인 수치해석 계산 결과에서 확보한 학습 데이터의 규모 확장, 검증할 수 있는 방법의 확충 등을 통해 계산 성능, 연산 시간 단축, 소요 에너지 감축 등의 발전을 이루어 갈 수 있을 것이기 때문이다. FEM이나 FDM은 여전히 많은 물리, 공학, 응용 과학 연산에서 가장 먼저 시도될 계산 방법론이 될 것이고, 역시 마찬가지로 병렬 연산 알고리즘이나 GPU 등의 하드웨어 기술 발전을 통해 연산 성능과 시간 단축 등에서 많은 발전이 이루어질 것이다. 또한 FEM, FDM 등의 계산에서 얻은 데이터는 해석적 해를 확보할 수 없는 사례에 대해서는 PINN에게는 좋은 학습 데이터가 될 것이고, 반대로 PINN에서 예측한 고차원 현상이나 시스템에 대한 데이터는 FEM, FDM에게 있어서 좋은 초기 추정치가 될 수도 있을 것이다. FEM이나 PINN 모두 현재는 주로 결정론적 PDE^{deterministic PDE}를 타겟으로 삼아 연산의 폭을 넓히고 있지만, 또 하나의 요구 조건은 확률론적 PDE^{stochastic PDE}와 역문제에서도 강력하고 신뢰도 높은 성능을 보여야 한다는 것이다. 이는 PINN과 FEM/FDM의 결합을 요구하는 것이며, 특히 역문제에서는 수치 불안정성의 증폭이라는 근본적인 문제를 공통적으로 앞에 두고 있는 상황에 대처하기 위함이기도 하다.

앞으로도 딥러닝 기반의 PINN 혹은 나아가 Physics-driven NN 등의 방법론이 적용될 수 있는 분야는 점점 넓어질 것이다. 그렇지만 연산이 가능한지 여부와 연산 결과가 정확한지는 전혀 별개의 문제다. PINN 역시 꾸준히 다른 수치해석 방법에서 얻은 결과는 물론, 실험치에서 얻는 결과와 비교하면서 정확도를 높이는 방향으로 발전해야 하고, 특히 실제 시스템의 물리적 특성을 보다 정확하기 이해하기 위해서는 각 분야의 도메인 지식을 충분히 반영하는 것이 중요하다. 예를 들어 Navier-Stokes 방정식을 이용하여 복잡한 미세 구조 내부에서의 액상-기상 혼합물의 유동을 모사하는 것은 지금도 기계공학, 화학공학, 소재공학, 물리학 등 관련 분야에서 난제 중의 하나로 남아 있다. 그런데 이를 모사하기 위해 애초에 Navier-Stokes 방정식이 아닌, 볼츠만 수송 방정식^{Boltzmann transport equation}을 계산하는 것을 골자로, 다소의 간략화를 거쳐 수립된 격자볼츠만모델^{Lattice Boltzmann Model, LBM} 같은 수치해석 방법론이 있다. 이는 네이비어-스토크스 방정식 자체가 분자 수준에서 보다 엄밀한 형태로 유도된 볼츠만 수송 방정식을 연속 공간으로 근사한 개념에서 출발한 지배방정식이라는 점을 고려한 것이다. 미세한 스케일의 공간에서 분자 단위로 유체의 흐름을 모사하기 위해서는 네이비어-스토크스 방정식보다는 볼츠만 수송 방정식을 직접 계산하는 것이 필요한데, 이러한 계산은 닫힌 형태로 주어지는 연속 시공간의 편미분방정식 계산으로 환원되지 않는다. 이를 우회하기 위해 LBM 같은 수치해석 방법론이 제시되었고, LBM 역시 D2Q9이나 D3Q19 같은 격자 기반 유한 요소 등이 도입되어 활용된다. LBM은 그 개념 상 미세한 공간의 특성이 반영되는 세밀한 경계조건을 고전역학에 기반한 방식으로 구현한다. 이러한 경계조건의 미세화는 일반적인 네이비어-스토크스 방정식에서는 구현되기 어렵다. 그 이유는 경계의 형태 변화가 지배방정식에서 고려하는 국부 곡률^curvature보다 작을 경우, 수치해석 과정에서의 오차가 증폭되기 때문이다. 때문에 미세한 영역에서의 유체의 흐름을 모사하는 경우에는 LBM의 방식으로 모사한 해석적 해가 보다 정확도가 높은 해를 주는 경우가 많다. 현재 LBM에서 얻은 데이터를 기반으로 PINN이 구현될 수 있는지를 테스트한 연구 결과는 전무하다. PINN은 앞서 언급한 것처럼 고차원의 해석에는 장점을 가질 수 있으나, 복잡한 경계조건이 주어지는 경우에는 약점을 보이고 있는데, PINN이 장차 극복해야 하는 전통적인 난제 중 하나가 바로 이러한 미세 경계조건이 국부적으로 변화무쌍한 케이스다. 따라서 PINN에 있어 가장 중요한 학습 데이터 중 하나는 LBM에서 얻은 수치해석 데이터가 될 것이다.

결론

PINN은 우리가 물리적 모형으로 모사할 수 있는 시스템이라면 앞으로도 일반적으로 적용될 수 있을 것이다. PINN이 보다 신뢰도 높은, 그리고 경제적인 계산방법론이자 수치해석 알고리즘으로 활용되기 위해서는 경계조건에 대한 취약성과 collocation points에 대한 랜덤 샘플링에 의한 계산 결과 변동성과 오차 증폭 가능성 방지, 학습 시간과 에너지 절약, 다른 수치해석 방법과의 크로스체크, 실험 데이터를 포함한 각 분야의 도메인 지식과의 유기적인 결합 등에서 더 많은 진전이 필요하다. 결국 고차원 물리적, 공학적 시스템과 현상 해석, 그리고 예측을 위해서 PINN은 앞으로 더 다양한 변용을 거쳐 더 많이 활용될 것으로 예상되기 때문에, 이러한 보강과 보완은 반드시 선행되어야 하는 작업이 될 것으로 예상된다.