시간 결정: 상상의 물질, 현실이 되는 여정

초대칭^{supersymmetry}이란 상호작용을 매개하는 보손^boson과 물질을 이루는 페르미온 ^fermion을 서로 바꾸는 대칭이다. (가까운 미래에 LHC 가속기에서 발견될 수도 있지 않을까 하는 기대를 해보지만, 현재까지는 가설적인 대칭이다.) 초대칭성을 가지는 끈을 초끈^superstring이라 하는데, 끈의 종류에는 두가지가 있다.

끈이론은 중력 그리고 양자장론^{quantum field theory}을 모두 포함한다. 예를 들자면, 닫힌 끈의 진동은 중력자^graviton을, 열린 끈 진동은 게이지 보손^{gauge boson}을 준다(각각의 초대칭 짝도 함께 기술한다). 

초등학교나 중학교에서는 물질의 상태를 고체, 액체, 기체로 구분한다고 가르친다. 워낙 경험적으로 친숙한 대상이라 굳이 과학자가 아니어도 무엇이 기체인지, 무엇이 고체인지 판별하는 게 어렵지 않다. 고체를 결정^crystal이란 말로 대신하기도 한다. 결정은 원자가 가지런히 주기적으로 정렬된 상태를 말한다. 원자가 한 방향으로 주기적으로 정렬된 상태는 1차원 고체, 두 방향으로 정렬된 상태는 2차원 고체라고 부를 수 있다. 우리 생활에서 익숙한 고체는 물론 3차원 결정이다.

미국 MIT 대학의 프랭크 윌첵은 천재로 분류되는 이론 물리학자다. 스무 살 약관의 나이에 쓴 논문으로 그의 지도교수와 함께 노벨 물리학상을 받았다. 그는 채 발견되지 않은 현상에 대해 이론적 상상을 즐긴다. 그가 제안한 액시온 이론, 애니온 이론은 모두 그 당시에는 존재가 확인된 바 없었지만 매우 그럴듯한 이유로 존재할 수도 있는 입자에 대한 상상력의 산물이었다. 그 중 애니온은 그가 이론적 제안을 한 같은 해, 실험적으로도 발견되는 기막힌 우연을 통해 물리학의 세계로 진입한 입자다. https://horizon.kias.re.kr/26440/

필자가 2014년 한 해를 MIT에서 안식년으로 보낼 때였다. 마침 윌첵이 하는 강의가 있다길래 청강을 해보았다. 일반 강의와는 달리 윌첵이 다루고 싶은 주제를 몇 개 골라 가르치는 ‘물리 오마카세’ 수업이었다. 그 중 한 꼭지가 ‘시간 결정^{time crystal}’에 대한 내용이었다.

윌첵은 상대성 이론에 친숙한 입자 물리학자다. 특수 상대론은 시간과 공간에 거의 동등한 수학적 위치를 부여한다. 미처 존재하지 않는 것을 상상하길 즐기는 윌첵은 ‘공간적으로 원자가 주기적으로 배열된 게 결정이라면 시간 방향으로 원자가 잘 정렬된 시간 결정도 있지 않을까?’라고 질문했다. 시간적으로 잘 정렬됐다는 건 결정이 마치 살아 숨쉬는 생물처럼 규칙적으로 크기가 변한다는 걸 의미한다. 일정한 시간이 지날 때마다 본래 부피로 되돌아오는 고체! 윌첵은 이 무모한 상상의 결과물을 시간 결정이라고 부르고는 2012년 두 편의 논문을 물리학 분야 최고 학술지에 출판했다 [1,2]. 어찌 황당한 아이디어로 논문을 쓸 수 있을까 싶기도 했지만 윌첵의 꿈은 현실이 되는 전례가 이미 여러 차례 있었기에 그의 시간 결정 제안을 가볍게 넘겨버릴 수도 없는 일이었다. 아니나 다를까, 그의 주장은 곧 고체의 물성을 연구하는 응집 물리학자들 사이에 회자되기 시작했고 그의 이론이 틀렸음을 보이는 반박 논문이 나오기 시작했다 [3,4].

반박 논문의 요지는 물질의 상태를 평형 상태와 비평형 상태로 엄격하게 구분짓는 이론인 통계 역학의 깊은 이해에서 비롯되었다. 평형 상태는 주어진 온도에서 어떤 물질이 취할 수 있는 가장 안정적인 상태를 말한다. 예를 들어 얼음 덩이는 영하의 온도에서 물분자가 모여 만들 수 있는 가장 낮은 에너지의 상태이다. 이런 평형 상태의 특징을 문학적으로 표현한다면 ‘아무 일도 일어나지 않는다’란 것이다. 다시 말하면 시간이 지나도 그 물질의 상태가 전혀 변하지 않고, 따라서 시간이 흐르는 것조차 알 수 없다는 뜻이다. 시간 결정이 존재한다면 시간에 따라 주기적으로 원자가 흔들리는 움직임이 있어야 할 텐데, 이것은 평형 상태란 말 자체의 정의와 어긋나버린다. 또 한편으론, 어떤 물질이 어떤 상태에 있다는 말은 평형 상태에서만 과학적으로 엄밀하게 정의할 수 있다. 가령 냉장고 속에 들어간 물이 얼음으로 변화하는 과정을 생각해 보면 이것을 물이라고 봐야할지 얼음이라고 봐야할지 불분명하다. 시간에 따라 차츰 물이 얼음으로 변화하고 있기 때문이다. 이처럼 시간에 따라 계속 물질의 상태가 변하는 경우를 두고 비평형 상태라고 부른다. 비평형 상태라면 평형 상태에 비해 훨씬 더 다양한 일이 일어날 수 있고, 주기적으로 진동하는 고체라는 것도 존재할 수 있을지 모른다. 그러나 윌첵이 야심차게 꿈꾸던 시간 결정은 평형 상태이면서도 주기적인 진동이 있는 새로운 물질 상태였다.

시계추를 생각해보자. 요즘은 자취를 감추었지만 예전엔 흔했던 괘종 시계에 매달린 시계추가 규칙적으로 흔들리던 모습을 쳐다보는 게 중장년 세대에겐 익숙한 추억이었다. 시계추의 느림이 느려졌을 때 태엽을 다시 감아주는 걸 그 당시 어른들은 ‘시계 밥 준다’고 표현했다. 물리학적인 표현으로 바꿔 보면 시계추에 에너지를 공급해준다는 뜻이다. 아주 단순한 시계추는 실에 매달린 무거운 돌덩이나 쇳덩이다. 우주공간처럼 마찰이 없는 곳에서 시계추를 작동시키면 따로 밥을 주지 않아도 시계추는 영구적으로 진동한다. 아쉽지만 이런 상태를 시간 결정이라고 부르지는 않는다. 물리학자들에게 물질이란 무수히 많은 원자가 모여서 이루어진 상태이다. 실생활에 존재하는 고체 역시 비록 유한한 원자로 구성되어 있긴 하지만 그 수가 워낙 많기 때문에 무한히 많은 원자가 모여 만들어진 고체와 그 성질이 다를 바 없다고 믿는다. 어떤 물질의 상태라는 것은 구성 입자가 무한히 많을 때에만 정확히 정의할 수 있다는 게 물리학자들이 오래 전 내린 결론이었다.

그럼 이번엔 우주 공간에 시계추를 무한히 많이 갖다 놓는다고 상상해 보자. 모두 동일한 시계추이기 때문에 진동하는 주기도 똑같다. 시간 결정이 만들어진 것일까? 무한히 많은 시계추로 구성되어 있고, 영원히 규칙적인 운동을 하지만 여전히 이 시계추의 집단은 시간 결정이 아니다. 가령 시계추 중 하나를 누가 몰래 다른 시계추로 바꿔버리면 그 순간부터 시계추의 집단은 더 이상 시간 결정이 아니다. 시계추 하나가 엉뚱한 주기로 진동하게 되었기 때문이다. 시계추끼리 주고받는 상호작용이 없다 보니 어느 한 곳에서 오류가 생겼을 때 이걸 스스로 보정할 능력이 없다. 작은 변화에도 금방 사라져 버리는 성질은 그 물질의 성질이라고 부르지 않는다. 변화에 저항하고 물질 고유의 성질을 유지하는 복원력은 구성 입자끼리의 상호 작용에서 온다. 즉 수 많은 동일한 시계추가 있어야 할 뿐 아니라 그 시계추끼리 서로 상호작용을 통해 한 곳에 오류가 생기면 그 오류를 즉시 보정할 능력도 자발적으로 갖춰야 비로소 시간 결정이 될 가능성이 생긴다.

이렇게 까다로운 조건을 하나하나 부과하다 보면 어느새 시간 결정은 이 세상에 존재할 수 없을 것만 같다는 걱정이 생긴다. 하지만 물리학자들은 끈질긴 노력 끝에 시간 결정이 만들어질 만한 조건이 무엇인지 찾아냈다. 일단 다체계 국소화된^{many-body localized}된 물질계가 필요하고, 여기에 주기적인 자극을 주어야 한다. 시간에 대해 주기적인 자극을 받은 물질계를 플로케^Floquet 계라고도 부른다. 물리학자들이 내린 최종 결론은 다체계 국소화된 플로케 물질계에서는 시간 결정이 존재할 수 있다는 것이었다.

본격적으로 시간 결정이 어떻게 구현되는지 설명하기 전에 짚고 넘어가야 할 점은 지금 우리가 이해하는 시간 결정은 윌첵이 처음 상상했던 것과는 상당히 다른 형태라는 것이다. 어쩌면 윌첵이 본래 주장했던 내용 중에 살아남은 건 시간 결정이란 이름과 새로운 물질 상태가 존재할지도 모른다는 희망과 기대감 뿐이었다고도 할 수 있다. 대가, 혹은 선도자의 역할이란 윌첵의 경우처럼 넓은 안목을 갖고 우리가 앞으로 주목하면 좋을 문제가 무엇인지 일러주는 것 아닐까 싶다.

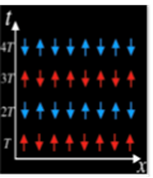
위의 그림1은 시간 결정이 시간에 따라 진동하는 모습을 간명하게 보여준다. 1차원적으로 배열된 자석을 상상해보자. 일상 생활에서 보는 큰 자석이 아니라 원자 크기의 작은 자석, 즉 스핀^spin이다. 평범한 물질계라면 외부에서 전자기장을 걸어주었을 때 원자 스핀 역시 전자기장이 떨리는 주기를 따라 함께 떨리는 게 정상이다. 초당 1번씩 주기적으로 바뀌는 전자기장의 영향을 받는 원자 스핀은 초당 1번 씩 회전하여 제자리로 돌아오는 식이다. 시간 결정에서는 그 주기가 두 배로 바뀌어 2초당 한 번씩 스핀이 제자리로 돌아온다. 비유를 들자면 이 물질 상태는 뫼비우스 띠 위에 존재하는 것만 같다. 뫼비우스 띠의 한 지점에서 시작해서 띠를 한 바퀴 돌면 제자리 대신 그 반대면에 도달한다. 한 바퀴를 더 돌아야만 비로소 출발점과 동일한 지점으로 돌아온다. 이런 현상을 물질계에서 구현할 구체적인 방법이 2016년과 2017년 사이에 출판된 세 편의 논문을 통해 정립되었다 [5-7].

여기 N개의 스핀이 있다고 하자. 처음 1초 동안은 외부에서 전자기파를 주입해 모든 스핀이 방향을 바꾸도록 한다. 가령 동쪽을 향하던 스핀은 서쪽, 서쪽을 향하던 스핀은 동쪽을 향하게 만드는 것이다. 다음 1초 동안은 스핀의 방향을 바꾸지 않는 다른 종류의 조작을 가한다. 스핀계가 이런저런 변화를 겪긴 하겠지만 초반 1초 사이에 뒤집힌 스핀 상태를 거의 그대로 유지할 것이다. 그 다음엔 최초에 가했던 전자기파 마냥 스핀의 방향을 바꾸는 조작을 또 1초 동안 한다. 스핀은 다시 뒤집힌다. 마지막 3-4초 시간 동안은 역시 스핀 방향을 바꾸지 않는 범위 안에서 이런저런 조작을 가한다. 잘 따져보면 스핀계에 해주는 조작은 2초 단위로 반복되었지만 스핀이 제자리로 돌아오는 데 걸리는 시간은 4초다. 본래 기대했던 조작 주기의 두 배의 시간이 걸려야 물질계가 제자리로 돌아오는 것이다. 시간 대칭성 파탄이 일어났다.

물리학자들은 결정이란 무엇인가, 그 정의를 두고 오래 심사숙고한 끝에 가장 중요한 요소는 대칭성 파탄이라고 결론내렸다. 결정이란 무엇인가? 일차적인 대답은 ‘원자가 규칙적으로 배열된 상태’이지만 이걸 달리 말하면 공간적인 대칭성을 깬 물질이라고 정의할 수도 있다. 온도가 높은 상태에서 존재하는 액체와 비교하면 그 의미가 분명해진다. 가령 물이란 액체 속의 물 분자는 그 위치가 물 속 아무데나 있을 수 있다. 섭씨 0도에서 물이 얼음으로 바뀌는 순간 물이 누리던 이 자유는 사라져버린다. 물 분자 사이의 간격은 일정하게 고정되며 그보다 더 가깝거나 더 먼 곳에는 물 분자를 놓을 수 없다. 원자가 공간 속에서 누리던 자유로움(물리학에서는 이걸 대칭성이라고 부른다)는 사라졌고 그 덕분에 얼음이란 결정 상태가 얻어졌다.

이런 대칭성 파탄의 입장에서 보면 시간 결정이란 앞서 설명한 것처럼 외부에서 조작하는 시간적 주기와는 다른 주기로 물질이 진동하는 경우를 가리킨다. 가령 외부에서 1초당 한번씩 물질을 흔들어주었는데, 막상 물질은 2초당 한번씩 진동한다고 하면, 이 물질은 1초마다 반복되는 외부 환경의 주기성을 자발적으로 깨뜨린 셈이 된다. 대칭성 파탄의 입장에서 보면 시간에 대한 대칭성을 깨뜨린 물질이니 시간 결정이라고 부를 수 있다. 가장 생각하기 손쉬운 경우는 외부에서 일정한 주기로 자극을 주어서 정확한 시간 주기성이 해당 물질에 부과되었을 때이다. 이런 경우는 물질이 진동하는 주기와 외부 자극의 주기를 구분하기 쉽기 때문에 어떤 물질이 시간 결정 상태에 진입했는지 그 여부를 판단하는 것도 상대적으로 쉬워진다.

일반적인 물질을 구성하는 원자는 받은 빛에너지를 고스란히 되뱉는다. 빨간색을 흡수하면 빨간색을 방출하는 식이다. 시간에 대한 대칭성이 깨졌다는 건 보라색을 흡수한 결정이 보라색 대신 빨간 색이나 노란 색 빛을 방출한다는 의미다. 입사한 빛과 다른 진동수의 빛을 내보내는 물질이 생소한 것은 아니다. 입사한 빛의 진동수에 비해 두 배짜리 진동수의 빛을 발생하는 2차 고조파 발생^{second harmonic generation} 물질이 있다. 하지만 이런 물질을 시간 결정이라고 부르지는 않는다. 고조파 발생은 그 물질 속 개별 원자를 통해 일어나는 현상이지, 결정 전체의 집단적 반응을 통해 주파수 변환이 일어나는 게 아니기 때문이다. 반면 시간 결정은 입사한 빛에 대해 물질이 집단적으로 반응하고 그 반응의 결과로 인해 입사한 빛과는 다른 주파수에서 집단적인 떨림이 일어난다. 원자가 개별적으로 반응하느냐, 물질 전체가 집단적으로 반응하느냐, 그 차이가 시간 결정 여부를 가른다.

시간 결정을 만드는 마법은 앞서 설명했던 두 단계의 조리 과정 중 두 번째 조리법에 숨어있다. 일단 스핀을 전체적으로 뒤집은 뒤 가해주는 조작은 스핀계를 다체계 국소화된 상태로 만들어주는 역할을 한다. 다체계 국소화된 스핀계의 거동은 사방에 장애물이 가득한 미로 같은 장소에 들어간 사람들이 어찌할 바를 모르고 우두커니 제자리에 서 있는 모습과 비슷하다. 2초 주기로 외부에서 변화를 주긴 하지만 후반 1초는 스핀이 다체계 국소화되어 우두커니 아무 변화도 움직임도 수행하지 못한다. 따라서 의미 있는 변화는 초반 1초 동안만 일어날 것이고, 스핀에 본래 모습으로 돌아가려면 외부 자극을 두 차례 가해야만 한다. 시간 결정의 마법은 이런 방식을 통해 이해할 수 있다. 이제 남은 숙제는 다체계 국소화가 무엇인지 이해하는 일이다.

아무리 잘 만든 결정이라고 해도 원자가 완벽하게 규칙적으로 배열되는 경우는 없다. 제자리에 있어야 할 원자가 다른 곳에 있기도 하고, 있어야 할 원자 대신 다른 원자가 그 자리를 차지하기도 한다. 완벽한 결정 상태에서 벗어나는 모든 경우를 묶어 무질서라고 표현한다. 우리가 관측하는 결정의 상태는 늘 이런 무질서는 어느 정도 동반한 상태다. 1950년대 미국의 응집 물리학자 필립 앤더슨은 전자가 무질서한 고체 속 공간을 이동하다보면 여기저기 무질서하게 배치된 벽에 부딪혀 멀리가지 못하고 제자리를 맴도는 ‘국소화’ 현상이 나타난다는 점을 증명했다. 전자가 입자라면 그다지 놀라운 결과가 아닐 수 있지만 고체 속 전자는 파동처럼 거동한다는 게 정설로 굳어진 시절, 입자가 아닌 파동이 한 공간에 국소화된다는 주장을 직관적으로 받아들이기는 쉽지 않았다. 예를 들어 잔잔한 호수 위에 돌을 던지면 입수 지점으로부터 파동이 퍼져 나간다. 입사 지점 주변에 몇 개의 말뚝을 박아 놓으면 어떻게 될까? 파동이 말뚝에 반사되어 되돌아오고, 퍼져나가는 파동과 서로 엉켜 간섭 무늬를 보인다. 말뚝이 제멋대로 여기저기 박혀있으면 어떻게 될까? 각 말뚝에서 반사된 파동은 서로 무질서하게 엉키고 간섭하는 바람에 본래 돌멩이가 입사한 지점에서 멀리 떨어진 지점에는 파동이 하나도 전달되지 않는다는 게 바로 앤더슨 국소화의 요지였다. 돌멩이를 동시에 두 개 던지면 어떻게 될까? 수십 개를 동시에 던지면? 동시에 수십개의 물결이 발생하고, 제각각 말뚝에 반사되면서 한층 더 복잡한 양상으로 물결의 국소화가 진행될 게 분명하다. 이런 상황에서 벌어지는 현상을 다체계 국소화라고 부른다. 다체계란 여러 개의 입자가 공존하고 그 입자끼리 상호작용하는 물리계를 뜻한다.

윌첵의 논문을 통해 시간 결정이란 개념이 세상에 나온지 불과 5년 만에 구체적인 시간 결정 조리법이 완성되었다. 곧이어 다음 해인 2017년에는 최초의 시간 결정을 만들었다는 소식이 두 연구진으로부터 나왔다 [8,9].

시간 결정의 한 사례는 이터비움(Yb, 원자번호 70)에서 전자를 하나 떼어낸 이터비움 이온을 모아 만든 다체계 이온계에서 구현됐다 [8]. 실험을 주도한 크리스 먼로^{Chris Monroe} 교수는 한국인 과학자 김정상 교수와 함께 이온 기반의 양자 컴퓨터 회사 IonQ를 창립한 원자 이온 물리학 분야의 전문가다. 이터비움 이온계에 레이저와 외부 자기장을 이용해 이론에서 제시한 방법대로 주기적인 조작을 해봤더니 이터비움 이온의 스핀이 주기적으로 회전을 하는데 조작하는 주기보다 두 배의 주기로 회전을 하더라는 사실을 발견했다. 정확히 이론이 예측한 대로였다. 다른 사례는 다이아몬드 속에 우연히 삽입된 질소 원자계(Nitrogen vacancy라고 부른다)에서 구현됐다[9]. 역시 질소 원자계의 스핀이 진동하는 주기가 조작 주기의 두 배라는 사실이 확인됐다. 당시 하버드 물리학과 대학원생이었던 최순원(현재 MIT 물리학과 교수)과 최준희(현재 스탠포드 전기공학과 교수)가 주도한 연구 결과였다. 두 실험이 공통적으로 보여주는 양상은 구동 주기에 비해 물질이 반응하는 주기가 두 배라는 점이었고 이 점은 시간 결정의 대표적인 특징이다.

시간 결정에 대한 고찰과 구현이 시사하는 바는 물리학자들의 관심이 평형 상태의 물질계에서 비평형상태의 물질계로 옮겨갔으며 이 과정에서 흥미로운 비평형 상태를 발견했다는 점이었다. 다른 시사점은 자연 상태에서는 자발적으로 이루어지기 어려운 상태가 인공적으로 만든 이온계나 다이아몬드 속 질소계와 같은 인조 물질에서는 구현된다는 점이다. 비평형 상태는 외부의 자극이 유지되는 동안만 존재하는 상태다. 시간 결정은 외부에서 규칙적인 자극이 주어지는 동안만 존재하다가 자극이 사라지면 함께 없어지는 덧없는 상태인 듯 하지만 존재하는 동안은 몹시 흥미로운 상태다. 사람의 심장과 호흡은 사람이 살아있는 동안만 규칙적으로 작동한다. 인생 역시 덧없지만 지루하지는 않다.

지금까지 합성하는 데 성공한 시간 결정은 수십 개의 원자로 구성된 양자 물질계였다. 시간 결정이란 요리를 만드는 데 중요한 재료 역할을 했던 다체계 국소화 현상은 원자를 파동으로 보고, 그 파동이 일으키는 간섭 효과에 기인한다. 윌첵은 시간 결정이 양자 물질계 뿐 아니라 공이나 구슬같은 고전적인 입자로 만들어진 물질계에서도 가능할 것이라고 보았다[2]. 시간 결정에 대한 이해가 깊어지면서 일부 고전역학계에서도 시간 결정과 마찬가지로 외부에서 걸어주는 자극에 비해 다른 주기로 진동하는 경우가 이미 알려져 있었다는 점이 드러났다. 이에 대한 이야기를 듣고 싶은 독자들에게는 논문[10]을 추천한다.