표준기저를 찾아서 [2]

일변수 다항식 대수

지난 연재 글에서 유리수체 \(\mathbb{Q}\) 위에 정의된 벡터공간의 예로

\(\mathbb{Q}[x] = \{ \mbox{변수 $x$에 관한 유리계수 다항식들} \}\)

을 제시한 바 있다. 참고로 읽을 때는 `큐엑스’라고 읽으면 된다. 이 벡터공간 \(\mathbb{Q}[x]\)에는 더하기, 상수곱 구조 외에 자연스럽게 곱하기 구조도 있으므로, 우리는 이것을 \(\mathbb{Q}\) 위에 정의된 대수^algebra라고 여길 수 있다.

일반적으로 체¹ 위에 정의된 대수^algebra란 원소 간 더하기, 원소와 (체 안에 사는) 상수의 상수곱이 정의된 벡터공간^{vector space}이라는 개념과 원소 간 더하기, 원소 간 곱하기가 정의된 환^ring이라는 개념이 서로 잘 공존하고 있는 대상이다.

지난 글에서 주어진 벡터공간의 모든 원소를 표현할 수 있게 해주는 가장 작은 집합인 기저^basis 중 어떤 것이 표준적^canonical이냐에 관한 논의를 시작했는데, 중간 결론으로 벡터공간 구조만 가지고서는 표준성 판단이 어렵고 추가적인 구조를 사용해야 표준성 판단 문제가 유의미해지며, 그러한 구조의 예시로 대수 구조를 들었다. 이번 글에서는, 우리에게 어떤 대수가 주어져있을 때 그 대수의 표준기저의 존재성에 대해 생각해보는 것을 기본 문제로 여기면 된다. 앞으로 살펴볼 바, 기저의 표준성을 판단하기에는 대수 구조만 가지고서는 여전히 부족한 편이며, 대수 구조에 더해 어떤 특별한 추가적인 구조가 있을 때 더욱 의미있는 분석을 할 수 있을 것이다. 본격적으로 들어가기에 앞서 지난 글에서 소개한 대로 위의 다항식 대수 \(\mathbb{Q}[x]\)의 기저에 대해 생각해보자. 가장 간단히 생각할 수 있는 기저로는 다음이 있다: 

\(B = \{ x^n \, | \, \mbox{$n \in \mathbb{Z}_{\ge 0}$}\} = \{1,x,x^2,x^3, … \} = \{\mbox{계수가 1인 $x$에 대한 단항식들}\}.\)

즉 \(\mathbb{Q}[x]\)의 임의의 원소, 곧 변수 \(x\)에 관한 임의의 유리계수 다항식 \(f(x)\)는 \(B\)의 원소들 유한개에 상수곱을 하여 더한 꼴인 \(f(x) = a_0 \cdot 1 + a_1 \cdot x^1 + a_2 \cdot x^2 + \cdots + a_n \cdot x^n\)로 유일하게 표현할 수 있다. 그런데 필자는 지난 글에서 이 기저가 생각만큼 그렇게 표준적인 기저는 아닐 수 있다고 주장한 바 있다. 혹자는 \(B\)를 `계수가 1인 단항식들의 집합’으로 깔끔하게 표현할 수 있으므로 이 정도면 꽤 표준적이지 않냐고 반문할 수도 있겠으나 (지난 연재 글의 용어로는 `감성적 표준기저’), 이 표현에서 눈여겨봐야 할 것은 무엇에 관한 단항식인지이다. 즉 `\(x\)에 대한’이 중요한 부분이다. 여기서 \(x\)는 대수 \(\mathbb{Q}[x]\)의 생성자^generator로서 역할을 하고 있다.

일반적으로 체 \(F\)위에 정의된 대수^algebra \(A\)의 생성집합^{generating set}이란 \(A\)의 부분집합 \(S\)로서, \(A\)의 임의의 원소를 \(S\)의 원소들과 체 \(F\)의 원소들의 더하기와 곱하기를 사용해 표현할 수 있다는 조건을 만족하는 것이다. 즉 개념상 벡터공간의 기저 혹은 생성집합^{spanning set}과 비슷하며, 이것들의 대수 버전이라고 볼 수 있다. 대수의 생성집합은 항상 존재하지만 유일하지는 않으며, 대수 \(A\)의 생성집합 하나를 골랐을 때, 그 생성집합의 원소들을 \(A\)의 생성자들^generators라고 부른다. 우리의 경우 체 \(\mathbb{Q}\) 위에 정의된 대수 \(\mathbb{Q}[x]\)가 있고, 원소 한 개 짜리 집합 \(\{x\}\)가 생성집합이 되므로, \(x\)가 \(\mathbb{Q}[x]\)의 생성자^generator라고 말할 수 있다. 결론적으로 \(\mathbb{Q}[x]\)의 임의의 원소를 \(x\)와 유리수들의 더하기와 곱하기만 가지고 표현할 수 있다는 말을 하고 있는 것인데, 실제로 이는 쉽게 확인할 수 있다. 편의를 위해 용어를 하나 정하자면, 만약 \(\mathbb{Q}[x]\)의 어떤 원소 \(y\)에 대해, 원소 한 개짜리 집합 \(\{y\}\)가 \(\mathbb{Q}[x]\)의 생성집합이라면, 우리는 \(y\)를 \(\mathbb{Q}[x]\)의 단일 생성자라고 부르기로 하자.

우리가 가진 문제는 대수 \(\mathbb{Q}[x]\)의 단일 생성자가 \(x\)로 유일하지가 않고, 매우 많다는 점이다. 예컨대 \(x-1\)도 단일 생성자의 예이고, 다른 예로는 \(2x\)도 있다. 독자들은 \(\mathbb{Q}[x]\)의 단일 생성자들을 금방 분류할 수도 있을 것이다. 여하간 이러한 단일 생성자 \(y\)를 하나 고르면, \(y\)에 관한 단항식들의 집합

\(B’ = \{1,y,y^2,y^3,\ldots\}\)

도 \(\mathbb{Q}[x]\)의 기저가 된다. 나아가서, 지난 연재글에서의 주장을 이어가자면, 만약 \(B=\{1,x,x^2,…\}\)가 대수적으로 `훌륭한’ 기저라면, \(B’\)도 \(B\)와 똑같은 정도로 훌륭하다. 실제로 이 둘은 엄밀한 의미에서 동일한 대수적 성질을 지닌다 (지난 글 참조). 그러므로 이 관점에서는, \(B\)가 \(B’\)보다 더 표준적이라고 하기가 어렵다. 따라서 \(B\)는 `공동 1등이 없이 단독 1등으로 대수적으로 훌륭한 기저’라고 보기는 어려우므로, 지난 글에서 제시한 바에 의하면 적어도 현재까지의 논의에 비추어볼 때 대수 \(\mathbb{Q}[x]\)의 기저 \(B\)를 \(\mathbb{Q}[x]\)의 표준기저라고 보기가 어렵다. 지난 글에서의 용어를 좀 더 충실히 따르자면, \(B\)를 `이성적’ 표준기저라고 보기 어렵다.

범주화

앞 절의 논의에서는 일견 간단해보이는 대수 \(\mathbb{Q}[x]\)에 대해서조차도, 그것의 대수적 구조만을 가지고서는 표준기저의 존재성을 판단하기가 쉽지 않다는 것을 살펴보았다. 이제 대수 \(\mathbb{Q}[x]\)에 모종의 자연스러운 추가적인 구조를 준 상황에서, 표준기저를 찾을 수 있는지 알아보고자 한다. 우선, 당분간은 이 특정한 대수 \(\mathbb{Q}[x]\)는 잊어버리고, 1990년대 정도부터 체계적으로 정립되기 시작한 `범주화^{categorification}‘라는 수학의 방법론을 대략적으로 살펴볼 것이다.

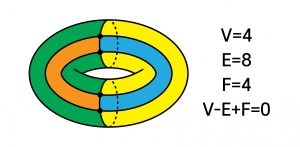
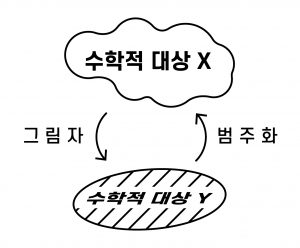
범주화는 어떤 수학적 대상을 자기보다 더욱 풍부한 구조를 가진 상위적 대상의 그림자와 같이 여기고, 상위적 대상의 풍부한 구조를 연구한 뒤 그 결과를 그림자에 해당하는 원래의 하위적 대상에 대한 결과로 환원시킬 수 있게 해준다. 오랫동안 잘 알려진 예시로, 기하적 대상들을 다루는 분야인 위상수학^Topology의 다양체^manifold라는 대상의 오일러 지표^{Euler characteristic}라는 개념의 범주화를 살펴보고자 한다. 다양체의 차원이 2인 경우가 곡면^surface인데, 그 중 `닫힌 유향 곡면’의 예시로는 그림 1과 같이 해변에서 가지고 노는 비치볼, 1인용 튜브, 2인용 튜브(!), 등등이 있다. 이러한 곡면에 매직펜으로 점을 몇 개 찍은 뒤, 점들을 잇는 선들을 서로 만나지 않게 그려 곡면을 다각형들로 분할해볼 수 있다. 여기서 다각형이란 위상수학적인 의미로, 선이나 면이 조금 찌그러져있어도 다각형으로 여기기로 한다 (그림 2에서는 예시로 1인용 튜브를 4개의 사각형으로 분할하였다). 이제 점의 개수를 \(V\), 선의 개수를 \(E\), 다각형의 개수를 \(F\)라고 하면,
$$ V-E+F $$
라는 숫자를 생각해볼 수 있다. 이 숫자는 정수인데, 이것이 그 곡면의 오일러 지표이다. 이 숫자는 내가 고른 곡면에만 의존하고, 그 곡면 위에 어떠한 다각형 분할을 사용했는지에는 의존하지 않는다. 즉, 새로운 다각형 분할을 사용해보면 \(V\), \(E\), \(F\) 각각은 변할 수 있지만 \(V-E+F\)의 값은 변하지 않는다.

또한 `위상적으로 같은’ 곡면들은 오일러 지표가 서로 같고, 위상적으로 다른 곡면들은 오일러 지표가 서로 다르다. 이 현상의 일례로, 어떤 곡면을 연속적으로 주물러서 변형시켜도 오일러 지표는 변하지 않는다. 따라서, 닫힌 유향 곡면마다 잘 정의되는 정수인 오일러 지표는 곡면에 대한 위상적인 정보를 어느 정도로 잘 담고 있는 위상적 불변량<sup>topological invariant</sup>로 여길 수 있다. 일반적으로 어떤 수학적 대상의 불변량<sup>invariant</sup>이란, 그 대상에 일종의 변형을 가해도 변하지 않는 수학적 양 혹은 대상을 지칭한다. 쉬운 예로는 유한집합이라는 대상의 `원소 개수’라는 불변량이 있으며, 벡터공간이라는 대상의 `차원’이라는 불변량도 있다. 불변량이라는 단어를 사용할 때에는 어떤 수학적 대상들을 다루고 있는지와 어떤 변형을 고려하고 있는지 정확히 말해주어야 하지만, 여기서 우리는 불변량에 대해 누군가 호라이즌에 글을 써주기를 기대하는 정도로 만족하고 넘어가기로 한다.

2차원보다 차원이 높은 다양체에 대해서도 위의 정의를 일반화하여 오일러 지표라는 정수값을 가지는 위상적 불변량을 얻을 수 있다. 이 오일러 지표라는 것이 다양체라는 위상적 대상에 대하여 꽤 유용한 정보를 주는 정수값 정보이기는 하지만, 다양체의 차원이 2보다 높은 경우는 특히 이 정수값이 다양체에 대해 모든 것을 말해주는 것은 아니다. 또한 2차원의 경우에 대해서조차, 지금이야 곡면을 하나 주고 \(V-E+F\)를 계산해보라고 하면 계산할 수는 있지만, 오일러 지표라는 개념이 발견되기 이전 상황을 가정하면, 곡면이 주어져 있을 때 애초에 왜 이런 특이한 방식을 통해 얻어지는 정수를 고려해야되는지 이해하기 어려울 수 있다.

오일러 지표보다 더 많은 정보를 담고 있고, 오일러 지표 자체에 대한 우리의 이해 역시 높여주는 대상이 있는데, 그것이 다양체의 호몰로지^homology이다. 호몰로지라는 것은 다양체 \(X\)와 음이 아닌 정수 \(n\)에 대하여 호몰로지 군^{homology group}이라고 불리는 가환군^{abelian group} 하나를 대응시키는 체계인데, 논의를 간단히 하기 위하여 유리계수 호몰로지만 고려해보면 \(X\)와 \(n\)마다 \(\mathbb{Q}\) 위의 벡터공간 하나를 대응시킨다고 여기면 된다. 이 벡터공간은 \(H_n(X;\mathbb{Q})\)라는 기호로 쓴다. 이 벡터공간의 차원을 \(X\)의 \(n\)번째 베티 수^{Betti number}라고 하고, 종종 \(b_n(X)\)로 쓴다. 적당한 조건을 만족하는 \(m\)차원 다양체 \(X\)가 주어지면 호몰로지로부터 베티 수들의 수열 \(b_0(X)\), \(b_1(X)\), \(b_2(X)\), …, \(b_m(X)\)가 대응된다. 이 숫자들이 위에서 말한 \(V\), \(E\), \(F\)와 비슷한 역할을 하며, 실제로 \(b_0(X) – b_1(X) + b_2(X) – …\)를 계산하면 그 결과가 위에서 언급한 오일러 지표와 동일함이 알려져 있다.

위 내용은 짧은 지면에 써놓기는 했지만 사실 꽤 복잡하고 신기한 이야기이며, 관심 있는 독자들은 `대수적 위상수학^{Algebraic Topology}‘ 교과서를 찾아보길 권한다 [1] (호몰로지의 쌍대 버전인 코호몰로지에 관한 글도 참조하면 좋다 [2]). 우리는 여기에서 이 이야기의 내용을 다 이해할 필요는 없고, 간단히 교훈만 얻으면 된다. 위에서 말하지 않은 중요한 사실 하나는 호몰로지 군 \(H_n(X;\mathbb{Q})\) 각각이 다양체 \(X\)의 불변량이라는 것이다. 불변량이라는 단어에서 불변량의 값은 항상 숫자여야 한다는 생각이 들 수도 있지만, 이렇게 때로는 좀 더 복잡한 수학적 대상이 불변량의 값으로 나오기도 한다. 이 유리계수 호몰로지 군들은 다양체의 정보를 담고 있는 벡터공간들이며, 우리가 그 벡터공간들의 모든 정보를 연구하는 대신에 그들의 차원만을 취해서 특정하게 더하고 빼서 얻어지는 하나의 정수가 오일러 지표인 것이다. 따라서 벡터공간인 호몰로지 군들에 대하여 어떤 명제를 증명하면, 정수인 오일러 지표에 대한 명제도 얻어낼 수 있게 된다.

각 벡터공간은 집합 구조, 더하기 구조, 상수곱 구조를 가지고 있으므로 각 정수나 자연수보다 물론 더욱 풍부한 구조를 가지고 있다. 실제로, \(X\)나 \(n\)을 바꿔가며 유리계수 호몰로지 군들 \(H_n(X;\mathbb{Q})\) 여러 개를 생각해보면, 이 벡터공간들간의 선형 사상^{linear map}, 즉 벡터공간 구조를 보존하는 사상들에 대하여 연구해볼 수 있다. 이에 비해 정수들 여러 개만 있을 때에 그들 간에 생각해볼 수 있는 것은 비교적 제한적이다.

정리해보면 “벡터공간은 음이 아닌 정수의 범주화를 제공한다”, “호몰로지 군들은 오일러 지표의 범주화를 제공한다”와 같은 말을 할 수 있다. 이들을 뒤집어 다소 비수학적으로 단순화해서 말하면 “음이 아닌 정수는 벡터공간의 그림자다”, “오일러 지표는 호몰로지 군들의 그림자다”라고 할 수도 있을 것이다.

이 틀에서 봤을 때, 내가 관심 있는 어떤 수학적 대상이 있을 때, 이 대상을 다른 무언가의 그림자로 여길 수 있게 해주는 그 `무언가’를 찾아내는 일이 `범주화’라고 볼 수 있다.

벡터공간과 대수의 범주화

앞 절에서는 정수의 범주화로 벡터공간을 제시했는데, 뛰는 놈 위에 나는 놈 있듯이, 우리는 이번에는 벡터공간의 범주화에는 무엇이 있을지 생각해보기로 한다. 지금까지 범주화를 언급하면서도 범주^category가 한 번도 등장하지 않았는데, 이제는 때가 되었다.

논의를 간단하게 하기 위하여 더하기와 상수곱을 가지는 벡터공간보다 조금 더 간단한 대상인 가환군^{abelian group}을 고려하자. 여기에는 상수곱은 없고 더하기만 있다. 이 글에서는 가환군의 간단한 예로 정수의 집합 \(\mathbb{Z}\)만 생각해보자. 우리는 \(\mathbb{Z}\)를 집합으로만 보는 것이 아니라 그것이 가진 더하기 구조까지 함께 고려하고, 이 가환군 \(\mathbb{Z}\)의 범주화를 찾아보고자 한다. 그럼으로써 실은 이전 절에서 얻은 정수의 범주화에 대한 논의를 좀 더 정밀하게 할 수 있게 될 것이다.

잠시 \(\mathbb{Z}\)를 잊어버리고, 유리수체 \(\mathbb{Q}\) 위의 벡터공간들과 이들에 대해서 할 수 있는 선형대수학^{linear algebra}에 대해 생각해보자. 우리는 유한차원 유리계수 선형대수학을 완벽히 섭렵하겠다는 꿈을 가지고, \(\mathbb{Q}\) 위의 모든 유한차원 벡터공간들을 한꺼번에 생각해보기로 한다. 이들이 함께 모여 “\(\mathbb{Q}\) 위의 유한차원 벡터공간들”이라는 `범주’를 이룬다. 편의를 위하여 이 범주를 \({\rm Vec}_\mathbb{Q}\)라고 이름 붙이자:

\({\rm Vec}_\mathbb{Q} = \mbox{$\mathbb{Q}$ 위의 모든 유한차원 벡터공간들의 범주}.\)

선형대수학을 한다는 것은 무슨 말인가? 그 핵심 중 하나로 우리는 각각의 벡터공간을 따로 따로만 보지 않고 그들간의 사상을 공부한다. 즉 이 범주에 들어있는 두 벡터공간 \(V\), \(W\)에 대하여, \(V\)에서 \(W\)로 가는 함수 \(f:V\to W\) 중 벡터공간 구조를 보존하는, 즉 다음의 조건을 만족하는 사상, 곧 선형사상^{linear map}들을 연구하고자 한다:

\(\mbox{모든 $v_1,v_2\in V$에 대해 $f(v_1+v_2) = f(v_1)+f(v_2)$}\),
\(\quad \mbox{모든 $v\in V$, $c\in \mathbb{Q}$에 대해 $f(cv) = c f(v)$}.\)

또한, 우리는 선형대수학만 하면 되고 예컨대 미적분학을 할 필요는 없으므로, 가능한 모든 함수 \(f:V\to W\) 중 선형사상만 공부하면 된다. 범주 \({\rm Vec}_\mathbb{Q}\)는 벡터공간들만 포함하는 것이 아니라, 그들끼리의 선형사상들에 대한 정보도 포함하는 개념으로 이해하자. 특별히, 두 벡터공간 \(V,W\)에 대해 서로 역함수인 선형사상들 \(f:V\to W\)와 \(g:W\to V\)가 존재하면 \(V\)와 \(W\)를 서로 동형^isomorphic이라고 부르기로 하자. 이 정의가 말이 되려면 선형사상의 합성의 의미와 항등 선형사상의 의미가 먼저 정립되어야 하는데, 선형사상들에 대한 그러한 개념들이 모두 범주 \({\rm Vec}_\mathbb{Q}\)가 포함하는 정보의 일부라고 가정하자.

선형대수학을 배우면 선형사상들에 대하여 여러 가지 성질들을 배우는데, 우리의 범주에 어느 정도의 성질까지, 어느 정도의 정보까지 포함시켜야 하는지는, 임의의 범주가 가져야 하는 최소한의 정보 외에는 개인이 정하기 나름이다. 이러한 최소한의 정보로는 위에서 언급한 사상들간의 합성과 항등사상이라는 개념을 예로 들 수 있다. 우리의 특정한 범주 \({\rm Vec}_\mathbb{Q}\)에 대해서 이러한 최소한의 정보 외에 선형대수학의 내용으로부터 생각해볼 수 있는 추가적 정보로는, 두 벡터공간 \(V\), \(W\)가 주어져있을 때, 이들을 이어붙여서 더 큰 벡터공간 \(V\oplus W\)로 만드는 직합^{direct sum}이라는 건설이 있다. 이 새로운 벡터공간은 집합으로서는 데카르트 곱공간인 \(V\times W\), 즉 \(V\)의 원소와 \(W\)의 원소의 순서쌍 \((v,w)\)를 모두 모은 집합으로 봐도 된다. 하지만 여기서는 곱보다는 `합’으로 이해하는 편이 수월함을 곧 깨닫게 될 것이다.

이제는 어느 순간 범주 \({\rm Vec}_\mathbb{Q}\)를 전부 공부하는 것에 지쳐서, 서로 동형인 벡터공간들은 그냥 같은 것으로 치자고 결심했다고 하자. 이것을 헷갈리지 않게 하려면 표기법을 개발해야 하는데, 벡터공간 \(V\)에 대해, 우리의 결심을 적용하고 나면 이것을 \([V]\)로 표기하기로 했다고 하자. 즉 \(V\)와 \(W\)가 서로 동형인 벡터공간이면 \([V]=[W]\)이고, 동형이 아니면 \([V] \neq [W]\)이다. 이 기호 \([V]\)를 \(V\)의 동형류^{isomorphism class}라고 부른다. 범주 \({\rm Vec}_\mathbb{Q}\)는 가능한 모든 벡터공간을 다 모아서 이루었지만, 이 결심을 적용하고 나서 동형류들만 모아보면 이제 훨씬 작은 모임이 된다. 예컨대 \(11\)세부터 \(29\)세까지의 다양한 사람들이 모여 있는 모임에서, 이제부터 `10대들은 모두 서로 동형이야’, `20대들은 모두 서로 동형이야’라고 선언하고 나면, 서로 다른 동형류가 많아야 두 개밖에 없어서, 동형류들의 모임은 원소가 두 개 이하인 작은 집합이 된다. 10대들의 동형류는 물론 그 구성원 중 하나를 아무나 잡아 [홍길동]과 같이 표현할 수도 있지만, 이 동형류에 이름을 붙여 \(\langle\)10대의 동형류\(\rangle\)와 같이 표현할 수도 있을 것이다. 다시 벡터공간으로 돌아오면, 우리는 선형대수학 시간에 벡터공간 \(V\)와 \(W\)과 동형인 필요충분조건이 이 벡터공간들의 차원이 같다는 사실을 알고 있다. 따라서 우리는 \(n\)차원 벡터공간 \(V\)의 동형류 \([V]\)에 이름을 붙여 예컨대 \(\langle n\rangle\)으로 표현할 수도 있을 것이다. 결론적으로는

\(\{\mbox{${\rm Vec}_\mathbb{Q}$의 동형류들}\} = \{ \langle n\rangle \, | \, n \in \mathbb{Z}_{\ge 0}\}\)

이 된다. 즉 범주 \({\rm Vec}_\mathbb{Q}\)의 동형류들만을 모으면 집합으로서는 그저 음이 아닌 정수의 집합 \(\mathbb{Z}_{\ge 0}\)으로 여길 수 있다. 여기까지는 사실 이전 절에서 이미 다룬 내용이다.

그런데 범주 \({\rm Vec}_\mathbb{Q}\)의 동형류들의 집합과 음이 아닌 정수의 집합 간의 이 대응은 집합으로서의 대응만은 아니고, 다음과 같이 좀 더 깊은 구조를 잘 보존하는 대응이다. 벡터공간의 동형류 두 개 \([V]\), \([W]\)가 있을 때 우리는 벡터공간의 직합이라는 개념을 사용해 \([V\oplus W]\)라는 새로운 동형류를 생각해볼 수 있으며, 한 편 음이 아닌 정수 \(n\), \(m\)이 있을 때 정수의 일반적인 더하기 구조를 사용해 \(n+m\)이라는 음이 아닌 정수를 생각해볼 수 있다. 우리의 표기법 상에서 \([V]=\langle n\rangle\), \([W]=\langle m\rangle\)일 때, 다음이 성립함이 선형대수학에서 알려져있다:

\([V\oplus W] = \langle n+m\rangle.\)

정리해보면, 음이 아닌 정수 \(n\)을 그저 숫자가 아니라 벡터공간의 동형류 \([V]\)로 볼 수 있으며, 이러한 대응 하에서 음이 아닌 정수 두 개의 합은 벡터공간 두 개의 직합의 동형류에 대응된다. 이 상황을, 직합이라는 구조를 지니는 범주 \({\rm Vec}_\mathbb{Q}\)가 더하기라는 구조를 지니는 음이 아닌 정수의 집합 \(\mathbb{Z}_{\ge 0}\)을 범주화한다고 이해할 수 있다. 즉 이전 절의 논의에 더하여 구조 한 가지를 더 살펴봄으로써 우리는 한 발을 더 내디딘 것이다. 한편, 우리는 벡터공간의 동형류와 직합만을 다뤘지만, 동형류끼리는 서로 뺄셈이 가능하다고 여길 수도 있다. 벡터공간들의 뺄셈은 일반적으로는 할 수 없지만, 벡터공간의 동형류들은 마치 음이 아닌 정수처럼 행동하므로 이들끼리는 추상적으로 뺄셈을 해볼 수 있는 것이다. 이렇게 동형류들의 집합에 뺄셈을 강제로 적용하여 얻어지는 구조를 그로센딕군^{Grothendieck group}이라고 부른다. 범주 \({\rm Vec}_\mathbb{Q}\)의 그로센딕 군을 취하면 가환군 \(\mathbb{Z}\) 전체가 얻어진다. 이에, 우리는

\(\mbox{“직합을 지니는 벡터공간의 범주 ${\rm Vec}_\mathbb{Q}$가 가환군 $\mathbb{Z}$를 범주화한다”}\)

고 말할 수도 있다. 단순화하면, 

\(\mbox{“벡터공간은 정수를 범주화하고, 벡터공간의 직합은 정수의 더하기를 범주화한다”}\)

라고 해석할 수 있다. 참고로, 좀 더 일반적인 범주의 그로센딕 군에서는 위와 같이 단순히 동형류만 다루면 안되고 좀 더 세밀하게 모종의 동치류^{equivalence class}를 다뤄야 한다.

원래 우리는 벡터공간을 범주화할 수 있는지 의문을 가졌지만, 벡터공간 중에서도 1차원인 \(\mathbb{Q}\), 그것도 모자라 상수곱을 포기하고 가환군 \(\mathbb{Z}\)만을 범주화하였다. 그런데 위에서 우리가 뺄셈을 강요했듯이, 위의 상황에서 유리수 상수곱도 강요할 수 있다. 그러나 우리는 이렇게 상수곱에 대하여 자세히 살펴보는 대신에 한 발 더 나아가서, 더하기 외에 곱하기 구조도 잘 범주화가 되는지 생각해보기로 한다.

우리가 이미 범주화한 가환군 \(\mathbb{Z}\)는 사실 자연스럽게 곱하기 구조도 가지고 있어서 환^ring을 이룬다. 재미있는 사실은 선형대수학에서 벡터공간 \(V\), \(W\)를 가지고 만들어낼 수 있는 새로운 벡터공간 중에 텐서곱^{tensor product} \(V\otimes W\)라고 부르는 건설이 있다는 것이다. 이것은 집합이나 데카르트 곱과는 성질이 매우 다르며, 현대 수학과 물리학의 여러 분야에서 매우 중요하게 쓰이는 개념이다. 벡터공간 두 개에 직합을 적용하면 차원이 더해지는 것에 반하여, 텐서곱의 경우 차원이 곱해진다. 즉, 위에서 약속한 표기법 상에서 \([V]=\langle n\rangle\), \([W]=\langle m\rangle\)일 때 다음이 알려져 있다. 

\([V\otimes W] = \langle nm\rangle.\)

따라서 위에서 얻은 가환군 \(\mathbb{Z}\)의 범주화 \({\rm Vec}_\mathbb{Q}\)는 사실 곱셈구조까지도 벡터공간의 텐서곱을 통하여 잘 범주화한다. 이를

\(\mbox{“벡터공간의 범주 ${\rm Vec}_\mathbb{Q}$의 그로센딕 환}\)^{Grothendieck ring}\(\mbox{이 정수 환 $\mathbb{Z}$를 복원한다”}\)

혹은

\(\mbox{“벡터공간의 범주 ${\rm Vec}_\mathbb{Q}$가 정수 환 $\mathbb{Z}$를 범주화한다”}\)

라고 표현할 수 있다.

이 절의 마무리로, 우리의 범주 \({\rm Vec}_\mathbb{Q}\)가 정수 환 \(\mathbb{Z}\)의 범주화로서 얼마나 `표준적’인지 잠시 고찰해보고자 한다. 벡터공간을 모두 모아놓고 그들간의 선형사상을 모두 고려하여 범주를 구성하고 나면, 이미 언급했듯이 임의의 범주가 가져야 하는 최소한의 정보도 있고, 우리가 우리의 특정한 범주에 대하여 생각해볼 수 있는 추가적인 정보를 고려할 수도 있다. 이 절에서는 선형대수학으로부터 배울 수 있는 벡터공간의 직합과 텐서곱이라는 개념을 우리의 범주의 추가적인 정보로 편입한 뒤, 우리의 범주가 정수 환을 범주화함을 확인하였다. 따라서, 마치 직합과 텐서곱이라는 특수한 개념들을 사용해야만 우리의 범주가 정수 환을 범주화한다고 여길 수 있다는 것처럼 느껴질 수 있다. 그런데 사실 직합은 임의의 범주가, 텐서곱은 임의의 `가환 범주’가 가져야 하는 최소한의 `표준적’ 정보들 중 하나라고 볼 수 있다. 즉 선형대수학 수업을 듣거나 책을 공부하지 않아도, 벡터공간와 선형사상의 정의, 그리고 범주론^{category theory}만 조금 알고 있으면 누구나 얻게 되는 꽤 표준적 연산들인 것이다. 물론 정말 누군가가 선형대수학 수업이나 책이 아니고 이러한 방식을 통해 우리가 직합이나 텐서곱이라고 부르는 연산들에 도달했다면, 아마 직합과 텐서곱에 해당하는 개념들에 대한 그만의 표기법을 개발했을 것이다. 범주론의 좋은 점 중 하나는, 이렇게 실질적으로 같은 개념이지만 표기법만 다른 경우 어떻게 그 개념들을 어떤 의미에서 같다고 여길 수 있을지에 대한 엄밀한 체계를 제공한다는 것이다.

대수의 범주화와 표준기저: 예고

이제 우리가 관심 있었던 대수 \(\mathbb{Q}[x]\)를 어떻게 범주화할 수 있는지 살펴봐야 할 것이다. 그런데 우리는 왜 범주화를 생각했던가? 그것은 물론 일반적으로 대수의 성질을 공부하는 중요한 방법이기는 하지만, 우리는 특별히 대수의 표준기저를 찾는 문제를 생각하고 있었다. 이 관점에서 범주화가 할 수 있는 역할은 다음과 같다. 주어진 대수를 잘, 되도록이면 자연스럽게 (가능하면 `표준적으로’!), 범주화하는 범주 하나를 찾았을 때, 만약 그 범주를 이루는 대상들 중에서 모종의 의미로 표준적인 대상들이 있다면, 그리고 그 대상들의 동형류가 원래의 대수에서 기저를 이룬다면, 우리는 이렇게 얻어진 기저를 표준적이라고 여길 수 있지 않겠는가?

우리의 대수 \(\mathbb{Q}[x]\)의 표준기저 문제에 실마리를 줄 수 있는 이러한 범주화의 예시를 소개할 차례인데, 아쉽지만 그것은 다음 연재 글에서 풀어보기로 한다.

그래서, 범주화란 무엇인가?

전체 연재를 아우르는 우리의 원래 목표는 표준기저였지만, 이번 글에서 다룬 범주화에 대해 좀 더 생각해보고 글을 마치고자 한다. 우리는 지금까지 범주화라는 단어를 체계적으로 정의하지는 않고 예시만 살펴보았다. 이 글을 읽고 난 뒤 범주화의 의미가 독자의 마음에 조금은 남을 수 있도록, `범주화란 무엇인가’라는 질문에 대해 수학적 대답과 비수학적 대답을 시도하기로 한다.

수학적 대답을 위하여, 이 범주화라는 단어와 개념에 대해 수학사적으로 간단히 살펴보면 좋을 것 같다. 이 글에서 언급된 오일러 지표, 베티 수, 호몰로지는 연구된 지가 백년이나 수백년은 된 것들이지만, 범주화라는 개념이 수학의 방법론으로 등장한 것은 1994년에 출판된 루이스 크레인^{Louis Crane}과 이고르 프렝켈^{Igor Frenkel}의 전설적인 논문 [3]에서이며 `범주화^{categorification}‘이라는 단어 자체도 해당 논문의 저자들이 처음 제안했다고 보는 것이 일반적으로 받아들여지는 견해이다. 이 논문에서는 이론 물리의 위상적 양자장론^{Topological Quantum Field Theory}에서, 차원이 하나 높은 위상적 양자장론을 건설하는 방법으로 범주화를 제시하였으며, 특별히 아직도 잘 이해되지 않은 4차원 위상적 양자장론에 대한 접근법으로 호프 대수^{Hopf algebra}를 범주화하는 호프 범주^{Hopf category}를 제안하였다². 요컨대, 범주화의 창시 취지는 아무 수학적 대상을 범주화하여 이해하자는 것이 아니라, 특정한 종류의 수학적 대상을 범주화하여 위상적 양자장론을 이해하자는 것이었다. 참고로, 표준기저의 범주화를 통한 이해 역시 이 초창기 취지에 포함되어 있다.

하지만 시간이 흐르며 범주화라는 단어는 원래 취지와는 다소 상관이 없이(!) 좀 더 일반적인 상황에서도 사용되게 되었다. 특별히, 수학적 대상 \(X\)가 수학적 대상 \(Y\)를 범주화한다고 했을 때, 우리는 꼭 \(X\)가 범주^category가 아니더라도 이 `범주화’라는 단어를 쓰곤 한다. 예컨대 이 글에서 처음 다룬 오일러 지표에 관한 예시에서는 \(Y\)가 정수 한 개이고 (오일러 지표), 이를 범주화하는 \(X\)가 유한 개의 벡터공간들이었다 (호몰로지군들). 그 다음의 예시에서는 \(Y\)가 가환군 (\(\mathbb{Z}\)) 혹은 벡터공간이었고, 이를 범주화하는 \(X\)는 모종의 범주였다 (벡터공간들의 범주). 이를 발전시켜서 \(Y\)가 환이나 대수일 때 (\(\mathbb{Z}\)), 이를 범주화하는 범주 \(X\)에 대해 생각해보았다 (텐서곱을 지니는 벡터공간들의 범주). 이보다 조금 더 심하게(!) 나아가면 범주화하고자 하는 대상 \(Y\)가 벌써 범주인 경우에, 이를 범주화하는 더 `심深한’ 또 다른 범주 \(X\)를 고려하는 경우도 있기는 하다. 다만, 필자의 경험 상으로는, 범주화라는 단어가 가장 널리 쓰이는 상황은 범주화하고자 하는 대상 \(Y\)가 대수 혹은 벡터공간이고, 이를 범주화하는 대상 \(X\)가 모종의 범주인 경우이다. 또한 본 연재에서 사용하려는 범주화도 이 경우이므로, 이 경우가 아닌 다른 상황에서의 범주화는 잊어버려도 좋다! 

\(\mbox{우리가 고려할 범주화 : 대수 혹은 벡터공간 $Y$} \leadsto \mbox{어떤 범주 $X$}.\)

이전 절에서의 논의에서와 같이, 범주 \(X\)는 직합과 텐서곱을 가지고 있어야 한다. 우리는 이전 절의 예시에서 정수들의 환 \(\mathbb{Z}\)를 범주화하는 것으로 벡터공간의 범주 \({\rm Vec}_\mathbb{Q}\)를 제시하였다. 여기서 \(\mathbb{Z}\)는 정수들의 모임이고 \({\rm Vec}_\mathbb{Q}\)는 벡터공간들의 모임이므로, 범주화를 도식적으로

\(\mbox{`어떤 대상’들의 모임 $Y$} \leadsto \mbox{`어떤 더 복잡한 대상’들의 모임 $X$}\)

로 이해하려는 독자도 있을 수 있다. 하지만 필자의 의견으로는 다음의 도식이 범주화를 좀 더 잘 표현해준다:

\(\mbox{`어떤 대상’들의 모임 $Y$} \leadsto \mbox{`어떤 다른 대상’들의 더 복잡한 모임 $X$}.\)

즉, `복잡함’의 방점은 `모임’에 있어야 하며, 위의 도식을 더욱 단순화하면 모임 \(Y\)를 범주화하는 것이 더 복잡한 모임 \(X\)라는 것이다 (물론 일반적으로 `어떤 다른 대상’은 `어떤 대상’보다는 더 복잡할 것이다). 더 나아가서는 사실 우리의 경우 모임 \(X\)와 모임 \(Y\)가 종류가 비슷하지만 \(X\)가 \(Y\)보다는 좀 더 풍부한 구조를 가지고 있는 상황이라기보다는, 모임 \(X\)와 모임 \(Y\)는 질적으로 다르며, 모임 \(X\)의 정보 일부로부터 모임 \(Y\)의 정보를 모두 복원할 수 있는 상황이다. 따라서 \(X\)가 \(Y\)보다 더 복잡하다고 하기보다는, \(X\)가 \(Y\)보다 `단계가 더 높다’라고 표현하는 것이 조금 더 정확할 것 같다. 원 논문 [3]의 취지를 살리려면 `차원이 더 높다’고 할 수도 있지만, 이것이 기하학적 차원에 꼭 대응하지는 않으므로 비수학적 용어로서의 단계를 사용하였다. 그러니까 \(Y\)가 \(X\)를 범주화하는 상황은 도식적으로

\(\mbox{모임 $Y$ $\leadsto$ 더 높은 단계의 모임 $X$}\)

혹은 

\(\mbox{수학적 대상 $Y$ $\leadsto$ 더 높은 단계의 수학적 대상 $X$}\)

로 보는 것이 좋다는 것이 필자의 주장이다.

이해를 돕기 위하여 범주화의 비수학적 예시를 들어보기로 하자. \(Y\)를 혈액형들의 모임 \(Y=\{A,B,AB,O\}\)이라 하고, \(X\)를 전 세계 모든 사람들의 모임이라고 하자. \(X\)의 각 원소인 사람은 혈액형 하나를 가진다. 혈액형으로 \(X\)에 동치 관계를 고려하면, \(Y\)는 \(X\)의 혈액형 동치류들의 모임으로 볼 수도 있다. 즉 이런 의미에서 \(Y\)를 \(X\)의 그림자로 볼 수 있다. 한편 \(X\)에서는 누가 누구와 함께 자식 누구를 낳았다는 관계를 생각해볼 수 있다. 이러한 원소들간의 생물학적 부-모-자식 관계가 \(X\)가 가진 구조 중 하나라고 여길 수 있다. \(X\)의 이 관계에서 혈액형 정보를 읽어보면, 부모의 혈액형과 자식의 혈액형간의 모종의 관계를 얻어낼 수 있다. 단, 논의의 단순화를 위하여 혈액형 돌연변이 현상은 없다고 가정하자. 예컨대 부모의 혈액형이 각각 \(A\)와 \(O\)라면 자식의 혈액형은 \(A\)나 \(O\)일 가능성은 있지만, 절대 \(B\)나 \(AB\)일 수는 없는 것이다. 그런데 이러한 혈액형 간 유전관계도는 \(X\)가 없이 \(Y\)만 가지고도 기술할 수는 있다. 만약 혈액형이라는 개념에 대해 전혀 모르는 사람(혹은 외계인)에게 혈액형이라는 개념을 처음 알려주고, 혈액형 간 유전관계도를 이야기해줬다고 하자. 이 사람은 아마 왜 유전관계도가 그렇게 되는지 이유를 알지 못할 것이기 때문에, 그 유전관계도가 맞는 이야기인지 혹시 오타가 없는지 아니면 단지 주장일 뿐인지 확신하기 어려울 수도 있을 것이다. 이제는 \(X\)의 부-모-자식 관계 전부를 알려주고 이들의 혈액형까지 알려주고 나면, 아마 아까 말해줬던 \(Y\)의 유전관계도에 대해 더욱 신뢰하게 될 것이다. 그러니까, \(Y\)가 가지고 있는 유전관계도라는 구조를 \(Y\)만 가지고서는 이해하기 어려웠지만, \(Y\)의 범주화인 \(X\)를 공부하고 나니 \(Y\)의 유전관계도 구조에 대한 이해가 증진된 것이다.

위 예시에서 \(Y\)와 \(X\)는 둘 다 모임이기는 하지만 \(X\)가 가진 구조가 \(Y\)보다 더 높은 단계라고 할 수 있다. \(X\)에서는 부-모-자식 관계를 생각할 수 있지만 \(Y\)에서는 없기 때문이다. 이런 상황에서는 \(X\)가 \(Y\)의 일반화라고 하기도 어렵고, \(Y\)에 구조를 추가하면 \(X\)를 얻을 수 있다고 하기도 어렵다. 또한 모임 \(X\)가 모임 \(Y\)보다 더 복잡한 모임이다라고만 표현하기에도 좀 부족하다. 예컨대 \((중학생들의~모임)\)은 \((초등학생들의~모임)\)보다 더 복잡한 모임일 수는 있지만 더 높은 단계의 모임이라고 하기에는 애매한데 비해, \(X=(중학생들의~모임)\)은 \(Y=(중학교들의~모임)\)보다 더 복잡한 모임이라기보다는 더 높은 단계의 모임이라고 하는 것이 나으며 어떤 면에서는 범주화의 예시로 볼 수도 있다. 실제로, \(Y=(중학교들의~모임)\)은 \(X=(중학생들의~모임)\)의 동치류들의 모임으로 이해할 수 있다. 결론적으로, 중학교들이 중학생들을 범주화하는 것이 아니라, 중학생들이 중학교들을 범주화하는 것이다!