우리가 사는 세상은 3차원, 경우에 따라서는 시간을 포함해서 4차원 공간이라고들 한다. 그렇다면 그보다 낮은 차원의 세상은 어떻게 이해해볼 수 있을까? 0차원은 옴짝달싹 못하는 점, 1차원은 앞과 뒤로만 움직일 수 있는 공간, 2차원은 앞뒤에 더해 왼쪽 오른쪽으로도 움직일 수 있는 공간이 될 것이다. 우리가 사는 3차원 세상은 키도 잴 수 있고 산도 오르고 아파트도 지을 수 있지만, 중력의 영향을 받는 우리는 2차원의 세계를 살아가는 것처럼 느끼곤 한다. 차를타고 점과 선과 화살표로 말하는 내비게이션의 말을 듣다보면 1차원 세계에 살고 있는것 같은 착각이 들기도 한다.
이 내비게이션이란 것을 조금 더 파헤쳐보자. 우리는 왜 내비게이션이 필요할까? 한국지도 위의 두 지점 A, B를 손가락으로는 쉽게 여행할 수 있지만 그 사이를 실제로 차로 이동하려면 정해진 선들로 상징되는 1차원 도로를 따라 이동해야한다. 안내는 어떻게 이루어지는가. 쉽게 말해 “갈림길이 나오기 전까지는 직진하고, 갈림길이 나오면 맞는 갈림길로 안내”를 반복한다. 결국 자동차 여행의 본질은 갈림길과 다음 갈림길 사이를 직진으로 달리고, 갈림길에서는 다음 직진할 장소를 고르는 것일 뿐이다. 수학에서는 이와 같이 어떤 대상들을 점으로 표현하고, 그 점들 간의 연결 상태를 나타낸 것을 그래프라고 정의한다.1
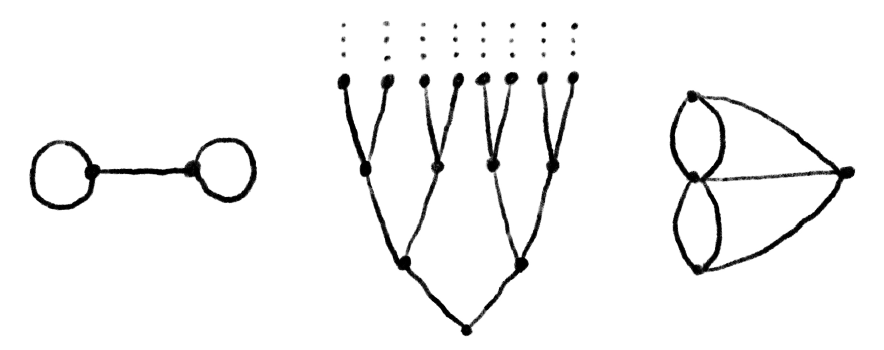
1. 그래프
그래프는 점들과, 점 사이를 잇는 선들로 정의된 대상이라서 이 세상의 ‘관계’를 시각화하기에 좋은 추상화 도구이다. 예를 들어 내가 속해있는 단체의 사람들을 모두 점으로 나타낸 뒤, 그 사이에 친구라면 선으로 잇는 방식으로 친목 그래프를 만들어볼 수 있다. 더 나아가, 친한정도에 따라 변을 굵게 설정하거나, 현실적으로는 친구관계란 비대칭 적인 경우가 있으므로 화살표를 넣어 친구라고 생각하는 방향(!)을 명시할 수도 있다. 이처럼 그래프는 실생활에서도 대상과 관계를 규명하는 유용한 도구이다.
수학적으로 정의하자면, 그래프는 꼭짓점이라 부르는 점과 변이라 부르는 선으로 이루어진 대상으로서, 각 변들의 양 끝이 꼭짓점과 연결되어 있기만 하면 된다. 이 때 변 양 끝이 같은 꼭짓점과 연결되어도 되고 (이런 변을 루프(loop)라고 부른다) 두 꼭짓점 사이가 여러 개의 변으로 연결되어도 된다. 그 외의 변 위의 다른 점에서는 꼭짓점과 만나선 안된다. 다시말해 변은 (서로 다를필요 없는) 두 꼭짓점들 사이의 연결여부만을 나타낼 뿐이다. 꼭짓점과 변의 개수가 모두 유한하면 유한 그래프, 둘 중 하나라도 무한하면 무한 그래프라고 한다. 우선 이번 글에서는 유한 그래프에 대해서 다루고, 이후 글에서 무한 그래프를 다루어 볼 것이다.
수학자들은 어떤 수학적 대상을 정의하고 나면, 그 대상이 가질 수 있는 구조를 생각해보고, 그리고 그 구조를 보존하는 대칭들을 생각해본다. 이는 마치 우리가 어떤 한 사람을 좋아하게 되면 그 사람이 좋아하는 음식과 취미 따위를 알아보고, 그것을 기반으로 주변에 맛집을 알아보고 대화를 해나가게 되는 것과 마찬가지이다. 우리는 그래프를 막 정의했으므로 어떤 구조를 줄지 먼저 생각해보자. 사실 정답이 있는 것은 아니지만, 우리는 그래프를 마음대로 늘였다 줄였다 할 수 있는 위상수학적 대상으로 생각할 것이므로, 길이가 정해져있는 구조는 주지 않기로 하되, 다만 그림 2에서와 같이 변을 잘라버리거나 두 꼭짓점을 가져와 붙여버리는 등의 ‘구멍의 개수’를 바꾸는 작업은 허용하지 않도록 하자. 이처럼 거리를 신경 쓰지 않으면서 대략적인 모양만 유지하도록 하는 것을 ‘위상수학적 구조’를 준다고 표현한다.
위상수학적 구조하에, 그래프에 자연스럽게 생각할 수 있는 대칭은 “연속변형동치 homo-topy equivalence” 인데, 이것은 쉽게 말해서 주어진 대상을 연속적으로 변형해서 만들 수 있는 대칭이다. 위상수학에서 흔히 커피 잔과 도넛이 같다고 말할 때 하나를 연속적으로 변형하여 다른 것을 만듦으로써 보여주곤 하는데 이 때 고려하는 대칭이 바로 연속변형동치이다.
물론 커피 잔과 도넛은 더 나아가 위상동형homeomorphic인 공간이 되기도 한다. 연속 변형동치는 “위상동형homeomorphism”보다 약한 대칭인데, 위상동형은 연속적으로 변형
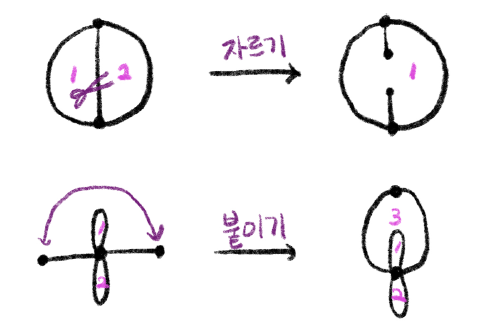
작업들. “자르기”는 구멍의 개수가 줄어들고, “붙이기”는 구멍의 개수가 늘어난
다.
가능해야 할 뿐 아니라, 서로 다른 점을 서로 다른 점으로 보내야하는 전단사성도 가지고 있어야 해서, 더 제한적인 대칭이다. 특히, 유한 그래프에서는 자기 자신으로 가는 위상동형들이 유한개 밖에 없어서, 실로 연속변형동치에 비하면 딱딱한 대칭이라고 할 수 있다.
이처럼 하나의 유한 그래프에 고려할 수 있는 위상동형들은 별로 없기 때문에, 조금 더 유들한 대칭인 연속변형동치들을 생각하기로 하자. 하지만 어떤 공간의 대칭이라는 것은, 사실 공간 위의 각 점이 어디로 가야할 지를 일일이 알아야 한다는 점에서 너무나 많은 정보를 갖고 있다. 따라서 이 정보를 조금 압축할 방법이 필요한데, 이런 철학으로 개발된 수학의 분야가 바로 “대수적 위상수학”이다.
2. 기본군
공간을 대수적 대상으로 압축하여 생각하는 방법을 소개하기 위해, 이 대수적 대상인 군Group 에 대해 잠깐 소개하도록 하겠다. 군에 대한 이야기는 다른 Horizon 기사에서도 많이 논의가 되었는데, 예를들어 [4] 등을 읽어보면 좋을 것 같다. 이 글에 맞추어 간단히 설명하자면, 군은 어떤 수학적 대상의 구조를 보존하는 “대칭”들의 모임이라고 이해할 수 있다. 대칭들을 모으면 어떤 성질을 만족하느냐? 일단 “아무것도 안하기” 항등원에 해당하는 대칭이 있고, 어떤 대칭을 하든 간에 “실행취소”를 하여 그것을 무를 수 있는 역원이 있고, 그리고 구조를 보존하는 두 대칭을 가져와서 한 대칭 뒤에 다른 대칭을 연달아 하면 그것도 통째로 구조를 보존하는 하나의 대칭으로 볼 수 있듯 대칭들의 “덧셈”이 잘 정의된다. 다시말해 군은 (굳이 숫자가 아니어도 되는) 추상적인 대상들로 구성되며 그들 사이의 “덧셈, 뺄셈을 논의할 수 있는 집합”인 셈이다.
기본군fundamental group이라는 것은, 어떤 공간을 대수적으로 압축하여 이해해보고자 하는 노력에서 정의된 대상이다. 일단 기하학적인 대상 중에 0차원은 점이고 너무 간단하니, 1차원 공간이 간단한 것 중에 가장 재미있는 공간이 될 텐데, 어떤 공간에 살고 있는 1차원 공간인 폐곡선들을 모은 것이 기본군을 이루는 집합이 된다. 이제 그림 3 을 보면서 읽으면 더 이해가 쉬울것이다. 여기에 연산을 잘 정의하기 위해서 폐곡선들의 “시작점”이 모두 공간위의 한 점으로 고정되어있다고 한다. 그러면 각각의 폐곡선들은 기본군의 원소가 되고, 두 폐곡선을 “더하려면” 두 곡선을 하나의 곡선처럼 이어서 생각하면된다. 역원을 정의해야 하니 폐곡선에 방향도 주기로 한다. 항등원은 “시작점에서 아무것도 안하는” 폐곡선으로 정의한다. 어떤 폐곡선의 역원은 방향만 뒤집으면 된다. 그리고 하나의 폐곡선을 연속변형해서 다른 폐곡선을 만들 수 있으면 기본군에서 같은 원소로 보기로 한다. 그러면 실제로, 왜 폐곡선과 그 역원의 곱은 “아무것도안하는” 항등원 폐곡선으로 연속변형 되는지를 알 수 있을 것이다.
예시를 생각해보자. 먼저 속이 빈 원기둥을 생각해보도록 하자. 그림 4 에서 볼 수 있듯, 사실 수직방향의 이동은 크게 중요하지 않고 몇 바퀴를 돌았는지가 기본군 내 원소의 변별력이 된다. 뫼비우스의 띠는 어떨까? 얼핏 다른 공간이지만, 폐곡선의 입장에서 생각해보면 역시 “몇 바퀴”를 돌았는지가 결국 관건이 된다.
두 공간 모두 모든 폐곡선이 몇 바퀴를 어느 방향으로 돌았는지로 결정되므로, 두 공간의 기본군은 같다. 두 공간이 같은 기본군을 갖는 것이 우연은 아닌게, 사실 그림 5 과 같이 두 공간이 모두 “원”으로 연속적으로 변형될 수 있기 때문이다. 실제로 원의 기본군의 원소들 또한 각 폐곡선이 몇 바퀴 돌았는지로 결정된다.
이처럼 기본군내에서는 연속되는 변형으로 얻어지면 같은 폐곡선으로 준다는 정의 때문에, 기본군에서 유용한 다음의 중요한 성질을 얻게 된다:
어떤 두 공간이 연속변형동치이면 그 두 공간의 기본군도 같게 된다.
이것이 기본군이 갖는 대수적 위상수학에서의 중요한 성질 중 하나이다. 다시 말해, 어떤 두공간이 연속변형동치인지를 알고 싶을 때, 두 공간의 기본군을 계산해보고 서로 다르면 연속변형동치가 아니라는 것을 알 수 있는 것이다.
그러면 자연스럽게 반대방향도 성립을 하는지 물어볼 수 있다. 즉 기본군이 같으면 두 공간이 연속변형동치인 것을 알 수 있는가? 애석하게도 그렇지 않다. 예를 들어, 구와 원판은 그 위의 폐곡선들을 점으로 연속변형할 수 있으므로 기본군이 자명하게 되지만, 서로 연속변형 동치가 불가능하다. 그 이유를 생각해보면 원판 자체는 점으로 연속변형동치가 되지만, 구는 어떻게 줄이고 늘려도 구 내에 갇혀있는 3차원 공간을 해소할 방법이 없기 때문이다.
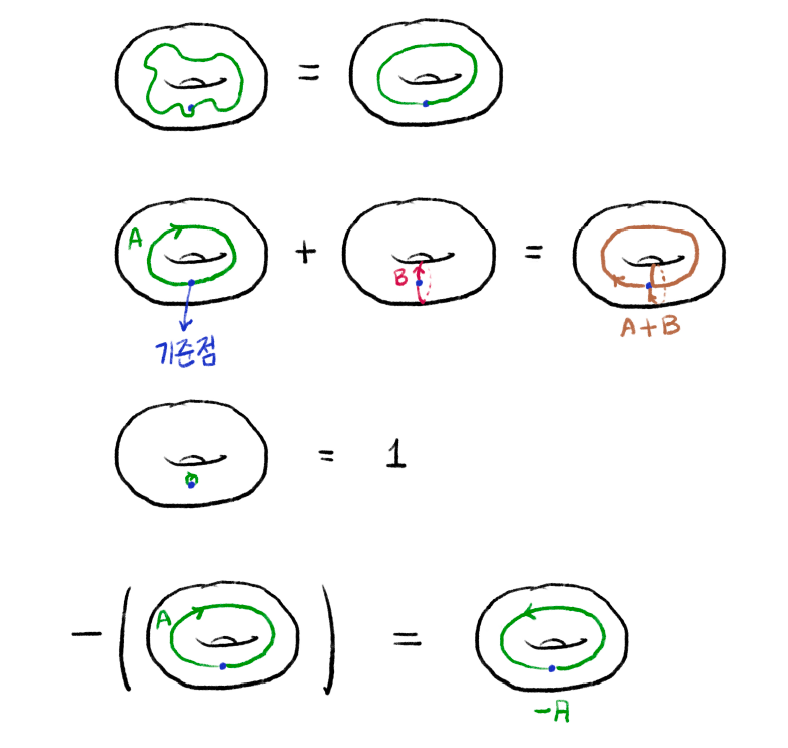
그림 3. 폐곡선의 덧셈, 항등원, 역원, 연속변형이면 같다
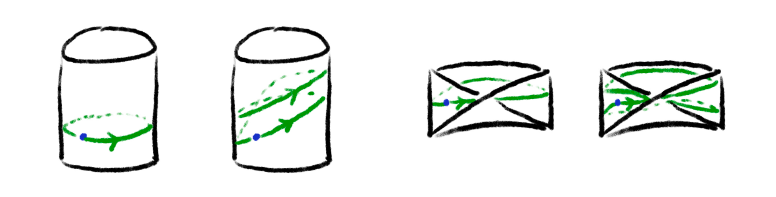
그림 4. 원기둥과 뫼비우스 띠 위의 폐곡선들
(이러한 아이디어를 이용하여 두 대상을 구분할 수 있는 새로운 불변량이 있는데 그것을 호몰로지homology라고 한다.)
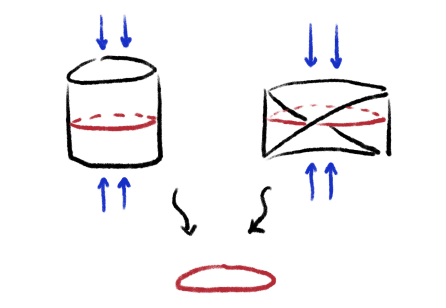
그림 5. 원기둥과 뫼비우스의 띠 모두 원으로 연속변형되는(“찌그러지는”) 모습
그런데 그래프의 경우에는 이 반대방향이 성립함이 알려져 있다. 즉, 두 그래프의 기본군이 같으면 사실 연속변형적으로 동치라는 것이다. 그 이유를 단순하게 생각해보면 다음과 같다. 기본군은 그 공간의 1차원 단위블록에 해당하는 폐곡선들을 모두 모아 압축한 공간인데, 동시에 그래프 자체가 1차원적인 수학적 대상이다. 따라서 그래프는 기본군으로 압축하는 과정에서 잃는 정보가 없어 그래프의 기본군은 그래프 그 자체에 대한 정보를 모두 갖고있게 된다. 이를 다시 말하면,
그래프에서 자기 자신으로 가는 연속변형들의 집합을 보는 것은, 그 그래프의 기본군에서 자기 자신으로 가는 자기동형사상들을 보는 것과 같다는 것의 의미가 된다.
이것이 상당히 중요한 패러다임의 전환인데, 바로 위상수학적인 대상의 질문을 대수학적인 질문으로 바꾸었기 때문이다. 이처럼 수학에서는 한 분야의 질문을 다른 분야의 질문으로 바꾸는 과정을 통해서 서로 다른 분야를 넘나드는 게 중요한데, 그 이유는 분야에 따라 발전된 수학의 형태가 다르고 이렇게 답을 모르는 질문의 형태를 바꾸어가다 보면 어느 순간 연구가 잘 되어있는 분야에 다다르게 될 수도 있기 때문이다.
3. 그래프의 기본군
그렇다면 그래프의 기본군을 알아볼 차례이다. 위에서 서로 연속변형동치인 공간은 같은 기본군을 준다고 했으니, 그래프를 잘 연속변형하여 기본군을 알기 쉬운 공간으로 바꾸면 좋을것 같다. 일단 꼭짓점들이 많아서 어느것을 기준점으로 해야할지 헷갈릴 수 있으니 꼭짓점을 하나로 만들면 좋을것 같다. 이를 위해, 그래프 위에 가장 큰 “생성나무”를 생각해보기로 한다.
생성나무란 무엇인가? 수학자들은 수학적 대상에 재미있는 일상적인 이름을 붙이는 것을 좋아하는데, 나무는 그래프의 특수한 형태로서, “싸이클”이 없는 그래프를 말한다. 또 다른 정의로는, 한 점에서 다른 점으로 가는 길이 유일하게 결정되는 그래프를 나무라고 한다. 어떤 그래프의 생성나무는 그 그래프에 들어있는 나무 중, 모든 꼭짓점을 포함하는 나무로 정의된다. 임의의 그래프를 가져오면 그것의 생성나무가 존재한다는것은 잘 알려져있다. 아래 그림에서 생성나무의 예시들을 살펴보면 그 존재성을 믿을수 있을것 같다.

이러한 생성나무를 하나 잡으면, 그것을 점차 줄이고 줄여서 점으로 만드는 과정은 연속변형으로 볼 수 있다. 이것이 의심스럽다면, 선분을 점으로 줄이는 것은 연속변형이라는 것이라는 사실에서 출발하여 생성나무의 가지 끝에서부터 점으로 줄여나가다 보면 귀납적으로 어떤 나무든지간에 점으로 줄이는 것이 연속변형동치라는 것을 알 수 있다.
그러면 그래프의 생성나무를 점으로 줄이고나면 어떤 그래프가 되는가? 바로 장미그래프가 된다.2
이 장미그래프에는 더할나위 없이 좋은 기준점이 있다, 바로 꽃잎들이 붙어있는 중앙점이다. 장미그래프의 기본군을 구하기 위해서, 장미그래프 위에 놓여있는 폐곡선들은 어떻게 나타낼 수 있을까? 조금 생각해보면, 모든 폐곡선들은 결국 어떤 잎을 몇 바퀴 어떤 순서로 돌았는지로부터 나타낼 수 있다. 이것을 코드화하여 각각의 꽃잎을 가나다 라고하고 그것을 역방향으로 도는것을 고노도 라고 하면, 가노노도고가다 등이 하나의 폐곡선을 나타나게 된다.
그런데 이렇게 가나다, 고노도로 나타낼 수 있는 원소들이 대수적으로 친숙한 대상인데, 바로 자유군의 원소들과 사실상 같은 녀석들이다. 자유군은 백형렬교수님의 Horizon 기사 [5] 에서 소개되었는데, “자유”가 붙은 이유는 가,나,다 와 고,노,도 로 만든 군이면서, 군의 정의에서 나온 가고=고가=1, 나노=노나=1, 다도=도다=1 의 관계식 외에는 제약하는 아무런 관계식이 없어서 그렇다. 이러한 자유군은 군론 내에서 “덩치가 큰 군”의 지위를 갖고, 특히 어떤 군들이 자유군들을 부분군으로 갖고있는지 등의 문제가 중요한 질문이 된다.
다시 정리하면, 우리는 그래프의 기본군을 보고자 그래프를 장미그래프로 연속변형을 하였고, 장미그래프의 기본군을 구하니 자유군이라는 것을 알게되었다. 즉 그래프의 기본군은 자유군이며, 이 자유군의 차수rank는, 장미그래프의 이파리 개수와 같음을 알 수 있다. 이로부터 위에서 주장했던 “두 그래프의 기본군이 같으면 두 그래프는 연속변형동치”라는 명제를 증명할 수 있게된다. 왜냐하면 두 그래프의 기본군이 같다는 것은 두 그래프의 자유군의 차수가 같다는 것이고, 곧 두 그래프를 같은 꽃잎의 개수를 가진 장미그래프로 연속변형을 할 수 있다는 의미이므로, 결국 두 그래프는 공동의 장미 그래프를 중간자로 하여 서로 연속변형 동치를 만들 수 있기 때문이다.
4. 그래프의 대칭군은 자유군의 외부대칭군
따라서, 그래프에서 자기자신으로가는 연속변형동치들의 모임은 자유군의 자기동형사상들의 모임과 같고, 그래프의 대칭군을 공부한다는 것은 결국 자유군의 자기동형사상들을 공부한다고 볼 수 있다. 수학기호를 하나도 쓰지않고 마치면 조금 아쉬우니, 이를 수학적으로 어떻게 적는지만 소개하고자 한다. 우선, 자유군은 Free group이라고 하며, 차수가 \(n\)인 경우에 주로 \(F_{n}\)이라고 적는다. 자기동형사상은 영어로 자기자신을 뜻하는 접미사 auto-와 ‘모양’의 어근을 갖고 있는 morph로 비롯된 함수와 변환을 뜻하는 -morphism이 합쳐져 automorphism이라 한다. 이 앞 세글자를 따서 자유군의 자기동형사상군은 Aut( \(F_{n}\)) 이라고 표기한다.
한편, 위상수학에서는 사상들 조차도 하나를 ‘주물러 다른 하나를 만들 수 있으면’ 같은 사상으로 보곤 하는데, 이러한 과정을 “연속변형” 이라고 하고 영어로는 homotopy라고 한다. 특히, 연속변형으로 같은 두 사상이 기본군에는 어떤 사상들을 주는지 생각해보면, 기준점이 연속변형 중에 그리는 자취가 또 하나의 폐곡선을 만들어냄에 따라 연속변형으로 같은 기본군에서는 서로 켤레conjugate인 사상을 주게된다. 이렇게 서로 켤레인 사상은 군 안의 “내부”적인 시선에서는 달라보이지만 “외부outer”에서는 사실상 같게 보인다. 우리는 연속변형으로 얻어질 수 있는 연속변형동치들을 같게 보고자 하므로 기본군에서는 켤레인 자기동형사상들끼리 하나로 묶고자 한다. 이 각각의 묶임을 외부자기동형사상outer automorphism 이라고 하고, 이런 묶음들의 모임을 “외부자기동형사상군” 이라 한다. 자유군의 외부자기동형사상군은 Out(\(F_{n}\))이라고 표기하며, 논의한 바와 같이 이 “자유군의 외부대칭군”이 곧 그래프의 대칭군, 즉 그래프에서 자기 자신으로 가는 연속변형동치들을 연속변형으로 얻어지는 사상들끼리 묶은 군이 된다.
위에서 서술하였듯, 다른 관점을 가지게 되는 것은 새로운 문제를 푸는 데에 도움이 된다. 예를 들어 Out(\(F_{n}\))은 대수적인 대상이지만, 그것의 부분군들이 어떠한 성질을 갖는지 [1, 2] , 각각의 원소들이 고정하는 부분군의 최대차수는 얼마인지 [3] 등등 많은 대수적인 문제들이 이 그래프의 위상수학적 대칭의 관점으로 풀렸다.
다음 글에서는 곡면과 곡면의 대칭군, 그리고 그래프와의 관계에 대해서 알아보고, 이후에는 무한한 곡면과 그래프에서는 어떻게 이야기가 일반화될 수 있는지에 대해 알아보도록 하겠다.
References
[1] Mladen Bestvina, Mark Feighn, and Michael Handel. The Tits alternative for Out(Fn). I. Dynamics of exponentially-growing automorphisms. Ann. of Math. (2), 151(2):517–623, 2000.
[2] Mladen Bestvina, Mark Feighn, and Michael Handel. The Tits alternative for Out(Fn). II. A Kolchin type theorem. Ann. of Math. (2), 161(1):1–59, 2005.
[3] Mladen Bestvina and Michael Handel. Train tracks and automorphisms of free groups. Annals of Mathematics, 135(1):1–51, 1992.
[4] 김상현. 경계에서 바라본 군. Horizon, 2019. https://horizon.kias.re.kr/9447/.
[5] 백형렬. 자유를 원한다면 탁구를 쳐라. Horizon, 2023. https://horizon.kias.re.kr/26251/.


