들어가며
내 전공이 암호학이라고 소개하면, 대개 “우와!”하며 신기해한다. 아마도 ‘암호’라는 단어가 주는 비밀스럽고 신비한 이미지 때문일 것이다. 나의 연구 분야 자체가 대화의 흥미로운 화제가 된다는 것은 감사할 일이지만, 이어지는 질문들은 종종 나를 당황스럽게 한다. 심지어는 친구들에게 “그럼 너가 <다빈치 코드> 작가보다 암호 잘해?”라거나 “그럼 박사 받으면 방탈출 카페 디자인하는 거야?”와 같은 질문까지도 받아봤다. 마음 같아서는 “암호학은 그런 게 아니야!”라고 단호히 외치고 싶지만, 마냥 쉬운 일은 아니다. 친구의 기대에 찬 초롱초롱한 눈빛 탓도 있겠지만, 그렇게 답하면 친구가 곧이어 되물을 게 뻔하기 때문이다. “그럼 암호학이 뭔데?”
몇 년 전, 한 SNS에 “현대암호학Modern Cryptography의 기점을 언제로 잡아야 할까?”하는 질문이 올라왔다. 여러 암호학자가 답글을 남겼는데, 네 편의 논문이 주로 거론되었다: (1) 섀넌Calude Shannon; 1916~2001의 1949년 논문, (2) 디피Whitfield Diffie; 1944~ 와 헬만Martin Hellman; 1945~의 1976년 논문, (3) 리베스트Ronald L. Rivest; 1947~, 샤미르Adi Shamir; 1952~, 애들먼Leonard Adleman; 1945~의 1978년 논문, (4) 골드와서Shafi Goldwasser; 1958~와 미칼리Silvio Micali; 1954~의 1982년 논문. 사실 현대암호학의 시작점을 하나로 정의하는 것은 다소 인위적이고 어쩌면 큰 의미가 없을지도 모른다. 하지만 그 기점으로 제안될 만큼 기념비적인 사건들은 분명 “암호학이란 무엇인가?”라는 근원적이면서도 답하기 어려운 질문에 대한 훌륭한 단서일 것이다. 본 연재에서는 위 네 논문의 문제의식과 성취를 되짚어보면서 현대암호학을 이루는 다양한 요소와 특질을 살펴보고자 한다.
본격적으로 현대암호학을 논하기에 앞서, 이번 글에서는 준비운동 삼아 그 이전의 세상을 잠시 살펴보자. 소위 고전암호학Classical Cryptography라고 불리는 분야다.
시저 암호
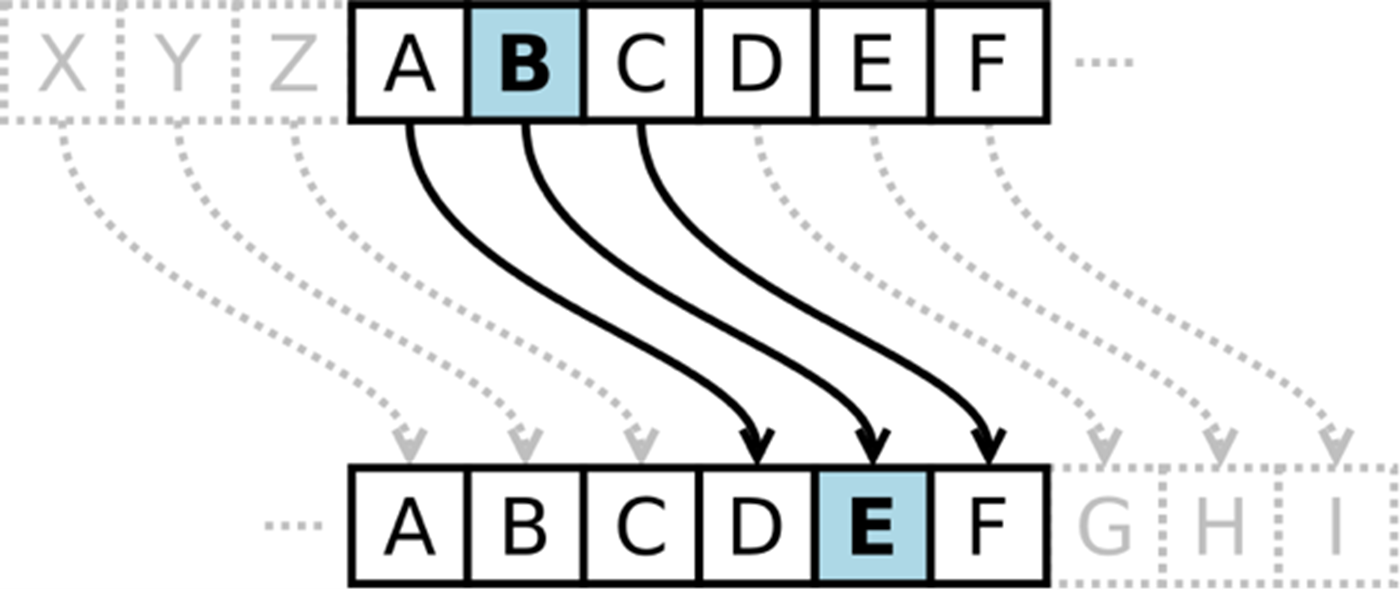
고전암호 중 가장 널리 알려진 것은 시저 암호Caeser Cipher일 것이다. 로마 황제 줄리어스 시저Gaius Julius Caeser; 100BC~44BC가 이 암호를 군사작전에서 사용했다고 전해진다. 시저 암호의 원리는 간단하다. 암호화하고자 하는 내용을 알파벳별로 일정한 거리만큼 “밀어서” 다른 알파벳으로 치환하는 방식이다. 이 때문에 Shift Cipher라는 이름으로도 불린다. 시저는 [그림.1] 처럼 알파벳을 세 칸씩 밀었다고 알려져 있는데, 이 경우에 ‘HELLO’를 암호화하면 ‘KHOOR’이 된다. 암호문을 다시 암호화되기 전의 상태인 평문으로 되돌리는 과정을 복호화라고 하는데, 시저 암호의 경우에는 암호화 과정의 반대 방향으로 동일한 거리만큼 밀어 주기만 하면 간단히 복호화할 수 있다. 시저 암호의 경우 알파벳을 얼마큼 밀지 결정하는 숫자가 바로 비밀키이며, 이 키는 암호 사용자들 간에만 공유되어야 하고 외부에 공개되어서는 안 된다. 시저는 비밀키 “3”을 사용한 셈이다.
그러나 시저 암호는 오늘날의 기준에서 전혀 안전하지 않다. 가장 큰 이유는 가능한 비밀키의 가짓수가 지나치게 적다는 점이다. 알파벳이 26자뿐이므로 가능한 비밀키는 단 26가지에 불과하다. 예를 들어 시저 암호로 암호화된 “KHOOR”에 대응하는 평문은 “GDKKN”, “HELLO”, “IFMMP” 등을 포함한 26가지 중 하나다. 이 중에서 실제로 말이 되는 것은 “HELLO”임을 확인함으로써 이것이 원래 평문이라는 것을 쉽게 유추할 수 있다. 즉, 암호화 방법이 공개되어 있다면, 가능한 경우의 수를 전수조사함으로써 암호문을 해독할 수 있다. 이 때문에 안전성을 위해서는 가능한 비밀키의 가짓수가 충분히 커야 한다. 컴퓨터 기술이 발전한 오늘날에는 적어도 \(2^{128}\)가지의 키조합이 가능한 암호화 방법을 사용한다. \(2^{128}\)이 얼마나 큰 수냐면, 나노초( \(10^{-9}\)초)마다 숫자를 하나씩 센다고 하더라도 \(2^{128}\)까지 세는 데에 100해(垓) 년이 넘게 걸린다. 참고로 과학자들은 우리 우주의 나이를 약 138억 년으로 추정하고 있다.
케르크호프스의 원칙
기민한 독자는 위에서 “암호화 방법이 공개되어 있다면”이라는 전제에 의문을 품으며, 그럼 암호화 방법 자체를 비밀로 유지하면 되는 것 아니냐고 반문할지도 모른다. 하지만 이는 암호학의 근본 원칙 중의 하나인 “케르크호프스의 원칙Kerckhoffs’s Principle”에 어긋난다. 19세기 암호학자 케르크호프스Auguste Kerckhoff; 1835~1903는 군사용 암호 설계를 위한 몇 가지 원칙을 제시하였는데 [3] 그중 가장 유명하고 중요한 원칙은 다음과 같다.
“암호화 방법은 비밀로 유지될 필요가 없어야 하고, 적의 손에 넘어가더라도 문제가 없어야 한다.”
비유하자면 자물쇠의 작동 원리가 공개되더라도 열쇠가 없다면 자물쇠를 열 수 없어야 한다는 것이다. 이렇게 보니 꽤 자연스럽게 들리지만, 왜 그래야 하는 걸까?
첫째, 비밀을 유지하는 데는 상당한 비용이 든다. 특히 크고 복잡한 비밀일수록 이를 관리하는 데에 더 많은 자원과 노력이 필요하다. 따라서 암호화 방법 자체를 비밀로 하기보다는 비밀을 키 하나로 집중시켜 관리 효율성을 높이는 것이 비용적인 측면에서 훨씬 합리적이다. 만약 자물쇠의 작동 원리 자체가 비밀이었다면, 누군가 와서 자물쇠를 관찰하고 분석하지 않을까 늘 대문을 감시하며 불편과 긴장 속에 생활해야 했을 것이다.
둘째, 비밀 유출로 인한 비용을 크게 절감할 수 있다. 영원한 비밀은 존재하지 않는다. 시저가 사용한 암호화 방법이 오늘날까지 전해진 것도 그 비밀이 결국 새어 나갔기 때문이다. 암호화 방법이 유출될 때마다 처음부터 새로운 암호화 방법을 설계하는 것은 현실적으로 부담이 너무 크다. 반면에 비밀을 키에 집중시킨다면, 키가 유출되더라도 간단히 새로운 키로 교체하는 것만으로 문제를 해결할 수 있어 훨씬 실용적이다.
셋째, 암호화 방법을 공개하면 더욱 폭넓은 검증의 기회를 얻을 수 있다. 시간이 흐를수록 다양한 전문가들이 공개된 암호화 방식의 취약점을 분석하고 개선 방법을 제안하여 안전성이 꾸준히 강화된다. 이는 오늘날 암호학에서 오픈소스를 장려하고 표준화를 추구하는 핵심 이유 중 하나다. 반대로 암호화 방법을 비밀로 유지한다면, 검증은 소수 내부자에 제한될 수밖에 없고 끊임없이 비밀이 유출되는 것에 대한 불안에 시달려야 한다.
치환암호
다시 고전암호로 돌아와서, 더 안전한 암호를 설계하기 위해 시저 암호를 확장해 보자. 시저 암호는 평문의 각 알파벳을 일정한 거리만큼 밀어 다른 알파벳으로 대응시키는 단순한 방식이었다. 하지만 대응 규칙이 꼭 이렇게 단조로울 필요가 있을까? 알파벳을 일정한 거리만큼 미는 대신 임의의 순열permutation을 기준으로 대응시키면 어떨까? 나아가 알파벳이 아닌 서로 다른 어떤 기호들에 대응시키는 것도 가능하다. 이렇게 임의의 순열로 확장한 방식을 치환암호Substitution Cipher라고 부른다. 치환암호에서 비밀키는 알파벳과 기호들을 대응시켜 주는 치환표이다. 예를 들어, 영어 알파벳 기준으로 가능한 비밀키의 가짓수는 기호들을 치환표에 배열하는 모든 가능한 경우의 수, 즉 \(26!\)이다. 이 값은 약 \(2^{88}\)에 해당하며 \(2^{128}\)에는 미치지 못하지만 여전히 천문학적으로 큰 수이다. 그럼 과연 치환암호는 이러한 거대한 키 공간 덕분에 충분히 안전할까?
추리소설 시리즈 <셜록 홈즈>의 <춤추는 사람>The Adventures of the Dancing Men; 1903편에서, 명탐정 셜록은 치환암호를 해독하여 사건을 해결한다. 이 때문에 적지 않은 독자들은 치환암호가 “빈도분석Frequency Analysis“에 취약하다는 것을 이미 알고 있을 수도 있다. 가령 이런 식이다. 영어를 기준으로 암호문에서 가장 빈번하게 등장하는 기호는 평문 “E”에 대응할 가능성이 높다. 이는 영어에서 “E”가 12.7%로 가장 자주 사용되는 알파벳이기 때문이다. 특정 기호가 모음인지 자음인지도 앞뒤 기호의 분포를 관찰함으로써 유추할 수 있다. 모음은 거의 모든 알파벳 앞뒤에 올 수 있는 데에 반해 자음은 특정 알파벳 앞뒤에만 오는 경향이 있기 때문이다. 물론 이것들은 통계적 경향이라 편차가 있지만 빈도분석은 조사해야 할 치환표의 가짓수를 급격하게 줄일 수 있다.
어째서 이런 분석이 가능했을까? 그것은 치환암호의 암호화 과정인 치환이 평문의 통계적 성질을 그대로 보존하기 때문이다. 따라서 암호는 평문의 통계적 특성을 보존하지 않도록 설계되어야 한다는 것을 알 수 있다. 또한, 비밀키의 크기가 충분히 크다고 해서 암호가 반드시 안전한 것은 아니라는 점도 이 사례에서 드러난다.
물론 치환암호가 대중화되어 추리소설에 해독법과 함께 등장하게 되기까지, 그것이 첨단기술로 여겨지던 시절도 있었다. 유럽에서는 15세기부터 암호가, 그중에서도 치환암호가, 외교 서신에 본격적으로 활용되었다. 이에 따라 왕실과 교황청은 암호전담부를 설치해 안전한 암호화 방법을 개발하고 첩보 활동으로 얻은 암호문을 해독하는 임무를 맡겼다. 치환암호가 통계적 분석에 취약하다는 사실이 점차 알려지게 되면서, 암호설계자들은 치환암호의 안전성을 높이기 위해 다양한 기법을 시도했다. 아무 의미 없는 널null이나 직전의 문자를 지우는 백스페이스backspace에 대응하는 기호를 추가하여 암호해독가를 교란하거나, 단일 치환표 대신 여러 치환표를 순차적으로 교차 사용하는 다중문자polyalphabetic 방식을 도입해 통계적 분석을 더욱 어렵게 하기도 했다. 그러나 이러한 설계자들의 노력도 결국 암호해독가들의 기교들과 더 정교한 방식의 통계적 분석 기술에 의해 금세 무력화되곤 했다.
이런 치환암호의 변형과 그의 해독이 어떤 이에게는 생과 사를 가르는 문제이기도 했다. 스코틀랜드의 메리 1세Mary, Queen of Scots; 1542~1587는 그녀의 추종자들과 함께 잉글랜드의 여왕 엘리자베스 1세Elizabeth I; 1533~1603를 암살하려는 음모를 꾸미며, 은밀한 소통을 위해 치환암호의 한 변형을 사용하였다. 그러나 결국 왕실의 암호해독가에 의해 이 암호는 해독되었고 메리 1세는 반란죄로 참수당하고 만다. 만약 그녀가 더 안전한 암호를 사용했다면, 그 결과는 어땠을까?
완벽하게 안전한 암호
추리소설이라는 장르를 창시한 작가로 평가받는 에드거 앨런 포Edgar Allan Poe; 1809~1849는 아마추어 암호학자로 활동하기도 했는데, 암호설계자와 암호해독가가 벌이는 끊임없는 지적 공방으로 이루어진 암호학의 역사를 다음과 같은 말로 압축적으로 표현했다.
“인간 지성이 고안한 모든 암호는 결국 인간 지성에 의해 해독될 수밖에 없다. Human ingenuity cannot concoct a cipher which human ingenuity cannot resolve.”
흥미롭게도 포가 이 말을 남긴 1841년은 비즈네르Vigenère 암호가 16세기에 소개된 이후 여전히 “해독 불가능한 암호le chiffrage indéchiffrable”라는 별명으로 불리며 외교 및 군사 분야에서 활발히 사용되고 있던 시기였다. 하지만 마치 포가 예견이라도 한 듯 이 “해독 불가능한 암호”도 결국 몇 년 지나지 않아 찰스 배비지Charles Babbage; 1791~1871에 의해 해독되고 만다. 그 이후에도 치열한 공방은 끊이지 않았다. 제2차 세계 대전에서 앨런 튜링Allan Turing; 1912~1954이 나치군의 복잡한 암호체계인 에니그마Enigma를 해독하여 전쟁의 판도를 바꾼 일화는 대중에게도 널리 알려져 있다.
정말 에드거 앨런 포의 말이 옳았던 것일까? 과연 “완벽하게 안전한” 암호란 존재하지 않는 걸까? … 그런데 잠시 생각해 보자. 완벽한 안전성을 갖춘 암호를 설계하려면 무엇보다 먼저 던져야 할 질문이 있다. 바로 ‘암호가 완벽하게 안전하다는 것이 무엇을 의미하는가?’라는 질문이다. 당연한 얘기지만, 목표가 없다면 이를 달성할 수도 없다. 2000년이 넘는 시간 동안 많은 사람들이 암호를 설계하고 해독하는 데 집중했지만, 정작 암호의 안전성이 무엇을 뜻하는지 아무도 그 정의를 명확히 묻지 않았다. 암호 설계자와 암호해독가 사이의 끊임없는 공방 속에서, 암호의 안전성에 대한 수학적 정의를 최초로 묻고 답한 인물이 바로 정보이론의 아버지, 클로드 섀넌Claude Shannon; 1916~2001이다.
다음 글에서는 섀넌이 제시한 답 “정보이론적 안전성”에 대해 알아보도록 하자.
참고문헌
- Singh, Simon. The Code Book. Vol. 7. New York: Doubleday, 1999. (한국에는 출판사 [인사이트]를 통해 <비밀의 언어>라는 제목으로 번역 및 출간되었다.)
- Brassard, Gilles. "Technical perspective: Was Edgar Allan Poe wrong after all?." Communications of the ACM4 (2019): 132-132.
- Kerchoffs, Auguste. "La cryptographie militaire." Journal des sciences militaires(1883): 5-83.