그래프와 곡면의 동상이몽 [2]: 곡면과 위상수학적 대칭

지난 글에서는 그래프와 그 대칭군에 대해 알아보았다. 이번 글에서는, 이 시리즈의 또 다른 주인공인 곡면과 그 대칭군에 대해 알아보려고 한다. 2차원 수학적 대상인 곡면은, 김현규 교수님의 글 [6] 에서처럼 수영장에서 볼 수 있는 비치볼과 튜브들로 생각해 볼 수 있다. 그림1은 [6, 그림1] 에서 먼저 제시되었다. 여기서 비치볼을 “\(0\) 인용 튜브”라고 생각하면, \(0\) 이상의 정수 \(n\)에 대해, \(n\)인용 튜브는 안팎을 구분할 수 있는 소위 유향곡면^{orientable surface}의 예시가 된다.¹ 그리고 이때 \(n\)을 해당 유향곡면의 종수^genus라고 부른다.

한편, 위상수학의 단골 손님인 “도넛”을 곡면의 예시로 혼동하기 쉽다. 일반적인 도넛은 속이 꽉 차 있는 3차원적 대상으로서 우리가 생각하는 2차원 곡면과는 엄밀히는 다른 대상이다. 굳이 도넛을 이용하여 곡면을 이야기하고 싶다면 도넛의 “껍질”이 곡면에 해당하며, 이 도넛 껍질, 즉 1인용 튜브 곡면은 토러스^torus라고도 부른다.

위에서 거론한 \(n\)인용 튜브들은 (물에 떠 있기 위해서라도) 구멍이 뚫려있는 부분이 없어서 닫힌곡면^{closed surface}이라는 특수한 곡면들이다. 한편, 이처럼 \(0\) 이상인 정수 \(n\)에 대해 \(n\)인용 튜브들을 전부 가져오면 닫힌유향곡면^{closed orientable surface}들을 빠짐없이 모으게 된다.

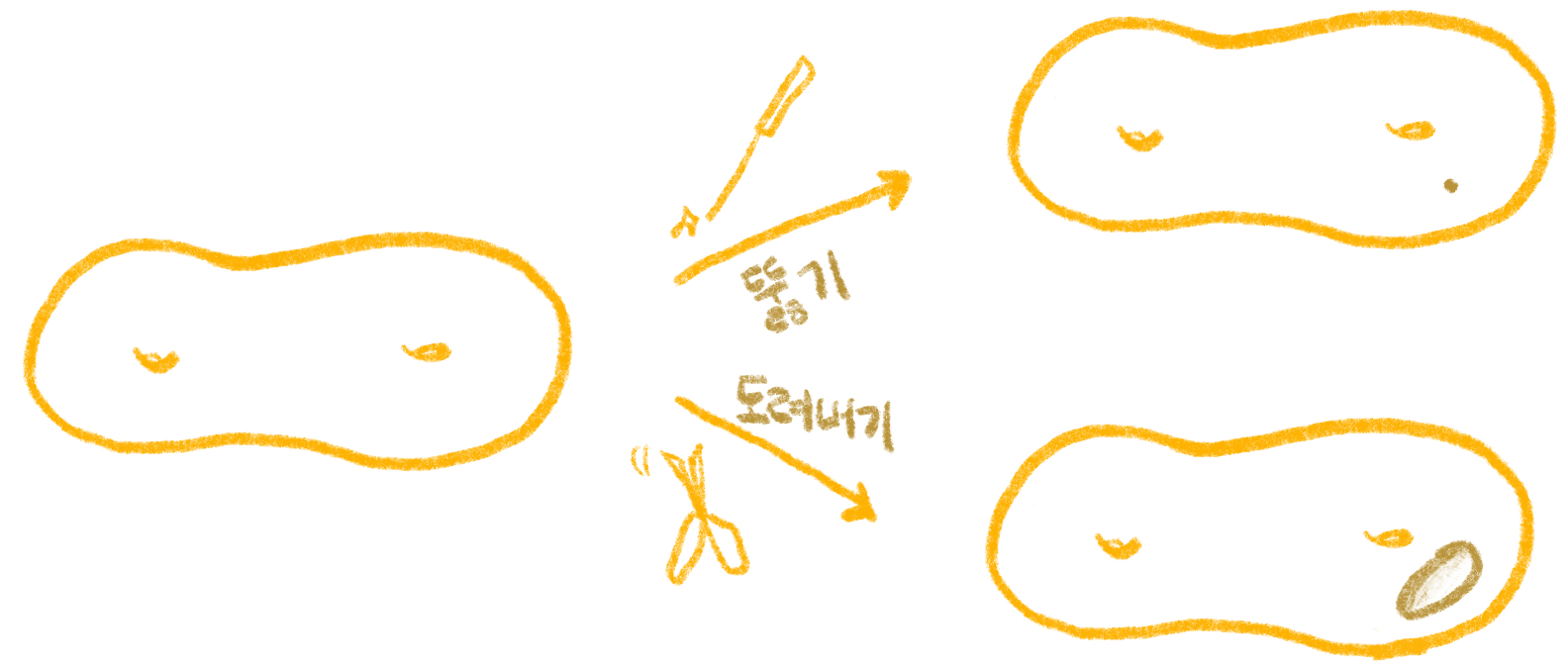
한편, 닫히지 않은 유향곡면을 만들고 싶다면 닫힌유향곡면에 구멍을 내면 된다. 구멍을 내는 것은 그림2와 같이 두 가지 방법이 있다. 하나는 매우 날카로운 송곳으로 곡면에 구멍을 뚫는 것이고 다른 하나는 가위로 곡면을 도려내는 것이다. 한편, 구멍을 뚫는 행위는, 실제로 구멍을 뚫지 않고 뚫으려던 점에 색깔로 점을 찍어 특별하게 취급하는 것과 동치이다. 이 두 구멍 냄을 구분하기 위해 두 작업으로 생겨난 구멍들을 각각 뚫은 구멍과 도려낸 구멍이라고 부르기로 하자.²

한편, 구멍을 내는 것 자체가 위상적 성질을 바꿀 뿐 아니라, 뚫음과 도려냄은 서로 다른 위상적 성질(구멍 주변의 경계의 유무)을 가진 곡면을 낳는다. 송곳으로 구멍을 뚫는 경우는 곡면에서 한 점을 제거하는 상황과 같고(마치 실수집합 \(R\)에서 0을 제거하듯), 가위로 도려내는 경우는 원판을 제거한 후 경계를 남겨두는 것과 같기(마치 \(R\)에서 \(0\)보다 크고 1보다 작은 수를 제거하면 0과 1이 남아 있듯) 때문이다. 이 때, 가위로 도려내어 제거한 원판의 둘레는 곡면의 일부로 남지만, 구멍을 뚫은 경우에는 “점 하나”의 둘레란 것이 없기 때문에 뚫은 구멍의 경계는 곡면에 존재하지 않는다.

이 두 변주를 이해하고 나면, 구멍의 개수와 종수 \(n\)이 유한한 유한 타입 유항곡면들은 \[ \text{(종수, 뚫은 구멍의 개수, 도려낸 구멍의 개수)} \] 순서쌍으로 완벽히 분류된다. 각 순서쌍에 따른 곡면의 예시로 그림3을 참조하라.

위상수학적으로 곡면의 대칭을 이야기할 때는 두 가지 대표적인 관점이 있다. 하나는 위상동형^{homeomorphism}으로서 곡면의 위상적 성질을 정확히 보존하는 변환들을 생각하는 것이고, 다른 하나는 그래프의 경우에서처럼 연속변형동치^{homotopy equivalence}로서 중간에 곡면을 자르거나 서로 다른 두 점을 붙이지 않고 연속적으로 변형하여 만들 수 있는 변환들을 생각하는 것이다. 모든 위상동형사상은 연속변형동치사상이 되므로, 곡면의 위상동형 대칭군은 곡면의 연속변형동치 대칭군에 속함을 예상해 볼 수있다. 이제 각 관점에 따라 대칭군이 어떻게 달라지는지 더 자세히 살펴보자.

1. 곡면의 위상동형 대칭군 — 사상류군 \(Map(S)\)

먼저 곡면 \(S\)의 위상동형사상을 모아 만든 대칭군을 살펴보자. 그래프에서처럼, 곡면의 위상동형사상 중 연속변형으로 같은 사상들끼리는 같은 원소로 보도록 하자. 그리고 \(S\)에 도려낸 구멍이 있다면 그 구멍의 경계를 움직이지 않는 위상동형사상만 고려하도록 하자.³이렇게 만든 곡면의 위상동형 대칭군을 사상류군^{mapping class group}이라고 부르고, \(Map(S)\)라고 쓰자. 여기서 mapping은 사상이라는 의미고, 서로 연속변형으로 같은 사상들끼리는 같은 “종류^class”로 간주하여 하나의 원소로 보고 있으므로 이른바 사상류^{mapping class}를 모은 군인 것이다.

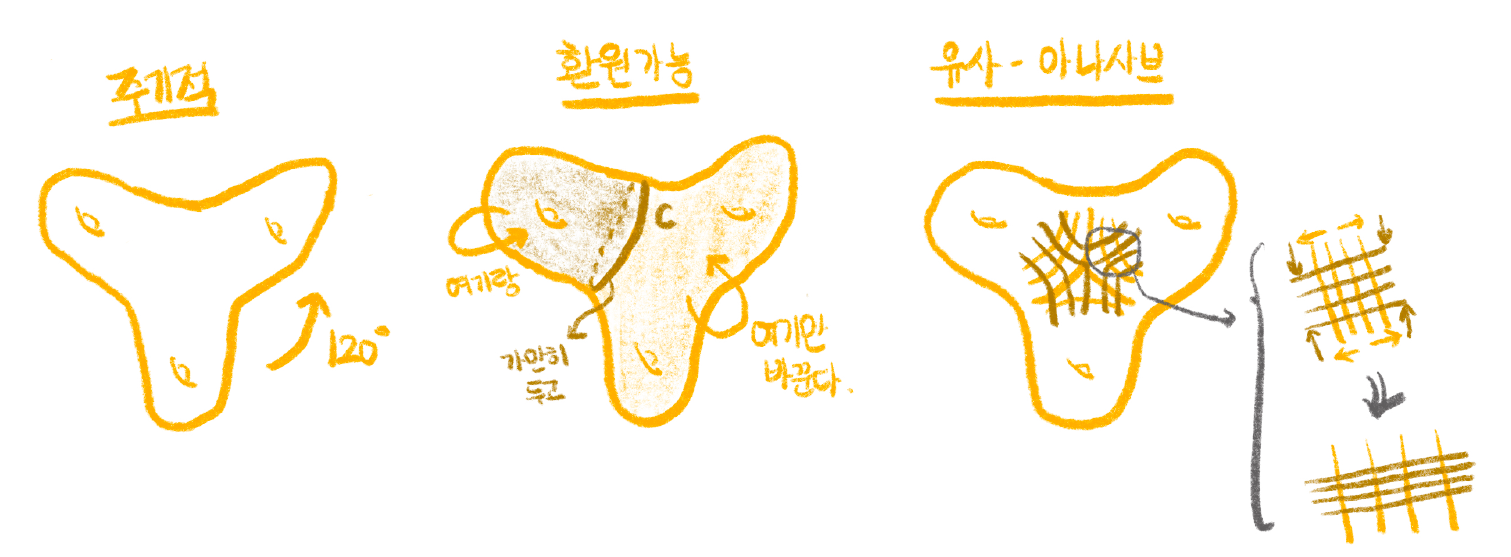
그래프에서처럼, 사상류군은 곡면의 대칭성을 연구하는 데 핵심적인 도구가 된다. 예를 들어, (종수가 1인) 토러스의 사상류군은 행렬군인 \(SL(2,\mathbb{Z})\)와 동형이며, 이는 \(2\times 2\) 정수행렬들 중 행렬식^determinant이 1인 것들을 모은 대수적 대상이다. 종수가 2이상인 유향곡면 \(S\)의 사상류군은 이렇게 깔끔하게 행렬군으로 나타나진 않지만, 닐슨-써스톤 분류정리⁴에 의해 \(S\)의 사상류들은 그림4와 같이 다음 세 가지 유형으로 분류된다:

A. 주기적^periodic 사상류: 유한 번 반복하면 항등사상(=곡면위의 모든 점을 가만히 놔두기)으로 돌아오는 사상류이다. 주로 곡면의 회전대칭에서 비롯된다.⁵

B. 환원가능^reducible 사상류: 곡면 위의 어떤 본질적인 단순폐곡선^{essential simple closed curve}을 보존하는 사상류이다. 이때, 본질적인 단순폐곡선이란 한 점으로 수축되지 않으며 (뚫은 혹은 도려낸)구멍 하나만을 고립시켜 감싸지 않는 폐곡선을 말한다. 이런 사상류는, 보존되는 폐곡선을 따라 자르면 나오는 더 단순한 부분곡면 위에서의 사상류로 “환원^reduce”하여 이해할 수 있다. 그림5의 우측에 표현된 덴 꼬기^{Dehn twist}는 환원가능 사상류의 중요한 예시이다.

C. 유사 아나사브^{pseudo-Anosov} 사상류: 곡면을 몇 개의 바둑판을 이어붙인 것으로 만든 뒤 가로줄, 세로줄 중 하나를 따라 길게 늘이고 다른 하나를 따라 짧게 수축시키는 변형이다. 가장 복잡하고 흥미로운 유형이다.

또, 길게 설명하지는 않겠지만 주기성과 환원가능성은 서로 배타적이지 않으나 (그림5 참조) 유사 아나사브 사상은 두 유형과 모두 배타적이다. 닐슨–써스턴 분류정리의 핵심은, 주기적이지 않고 환원가능하지 않은 모든 사상류가 유사 아나사브라는 것이다. 이는 마치 어떤 버스의 안내문에 “탑승 시 반입할 수 없는 것은, 1) 달콤한 음식이거나 2) 뜨거운 액체거나 3) 최근 5년 내 출판된 위상수학 논문⁶”이라고 적혀있는 것과 같은 결과이다. 실제로, 최인혁 박사님이 유사 아나사브 사상류가 사상류군의 “대부분”인 관점이 존재함을 증명[3] 하여, 유사 아나사브의 사상류군 내의 영향력을 재조명했다고 볼 수 있다.

2. 곡면의 연속변형동치 대칭군과 사상류군

이제 곡면의 연속변형동치를 살펴보자. 이전과 마찬가지로, 곡면의 연속변형동치를 다 모은 후 연속변형으로 같은 것끼리 하나로 본 군을 연속변형동치 대칭군이라고 하자. 결론부터 말하자면 그래프의 경우와 마찬가지로 곡면의 연속변형동치군은 그 기본군의 외부대칭군과 같다. 이 문장을 적절히 믿을 수 있다면 다음 문단을 넘어가도 좋다. 정확히 설명하려면 적잖은 이론이 필요하여, 대신 조금 부정확하지만 대략적인 직관을 소개하고자 한다.

일단 곡면의 연속변형동치는 그 곡면의 기본군에 자기동형사상을 준다. 역으로, (종수가 1이상인) 모든 곡면은 평면으로부터 “접어만들 수” 있는데(최인혁 박사님의 글 [2] 과 전보광 교수님의 글 [1, 그림 5, 6]을 참조하라.) 평면은 점과 위상적으로 다름 없는 아주 단순한 공간이다. 그 조상의 단순성 때문에 사실상 곡면의 심화군⁷들이 모두 자명해지므로 기본군만이 위상적으로 쓸모있는 정보로 기능하게된다. 따라서, 곡면의 기본군의 자기동형사상이 주어지면, (어차피 정보를 주지 못하는) 심화군의 보충정보가 필요없이 곡면의 위상적 대칭, 즉 연속변형동치를 복원할 수 있게된다. 끝으로, 그래프에서처럼 연속변형으로 같은 연속변형동치는 서로 켤레^conjugate로 같은 기본군의 자기동형사상을 준다. 따라서, 곡면 위의 연속변형동치류들 모으면 기본군의 외부자기동형사상을 모은 군과 정확히 같게된다.

그러면 위상동형으로 만든 사상류군과 연속변형동치 대칭군은 어떤 관계가 있을까? 일단 각각의 위상동형사상이 기본군의 외부자기동형사상을 주기 때문에, 사상 \[ \Phi: Map(S) \to Out(\pi_1(S)) \] 는 자연스럽게 주어진다. 이 사상 \(\Phi\)가 곡면 \(S\)의 종류에 따라 얼마나 좋은지를 기술하는 것이 바로 덴–닐슨–베어 정리⁸이다.

덴–닐슨–베어 정리. 종수가 2이상인 곡면 \(S\)를 생각하자. 만일 \(S\)가 닫힌곡면이면 \(\Phi\)는 동형사상이다. 만일 \(S\)에 도려낸 구멍이 없으면 \(\Phi\)가 단사⁹이다. 

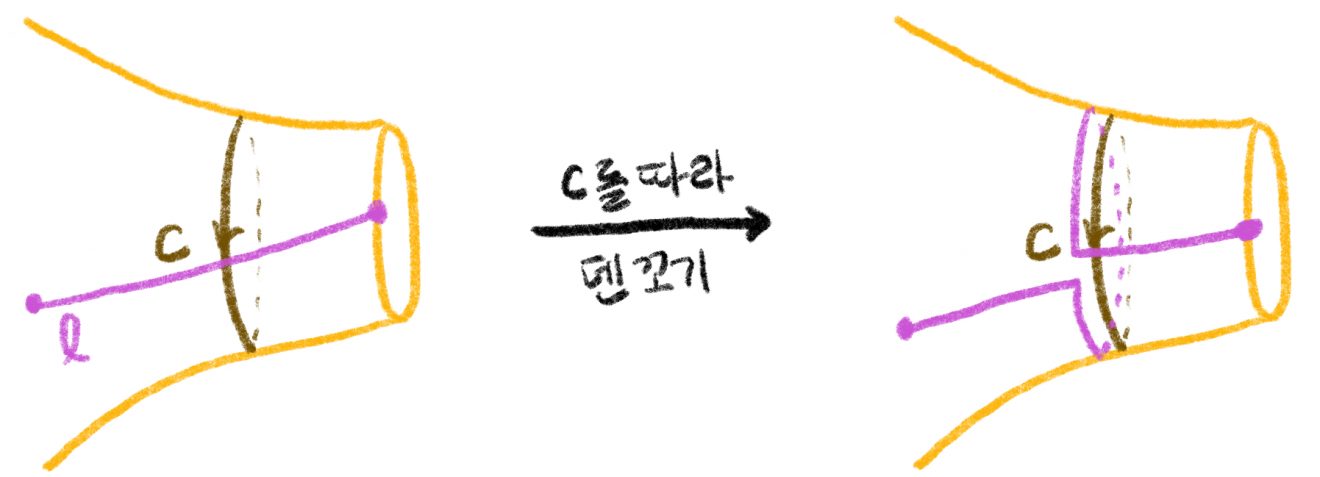
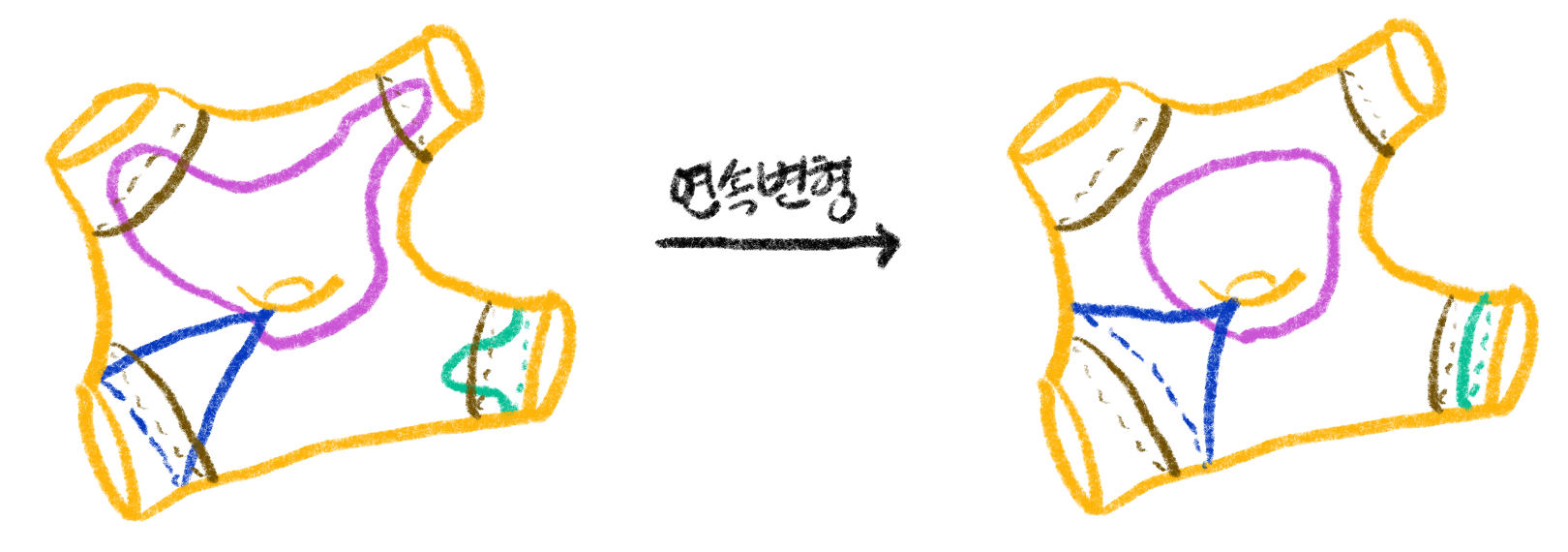
한편, \(S\)에 도려낸 구멍이 있는 경우 \(\Phi\)가 더 이상 단사는 아니지만, \(\Phi\)로 인해 “자명한 대칭으로 가는 원소들의 집합”(=핵; kernel)은 도려낸 경계를 두르는 곡선을 따라 만든 덴 꼬기들로 생성된다. 사상류군을 정의할 때 경계를 가만히 두는 위상동형만을 모았기 때문에 도려낸 구멍을 따라 도는 덴 꼬기는 사상류내에서 비자명한 원소가 된다. 그림6을 참조하라.¹⁰ 반면, 뚫린 구멍을 휘감는 곡선을 따라 만든 덴 꼬기는 사상류내에서 자명한 원소가 된다. 그림7을 참조하라.

그렇다면 왜 도려낸 구멍을 따라 도는 덴 꼬기는 \(\Phi\)에 의해 자명한 원소로 가는 것일까? 덴 꼬기는 꼬는 곡선과 만나는 선에만 영향을 줄 수 있는데, 곡면위의 모든 폐곡선은 도려낸 구멍을 휘감는 폐곡선들과 만나지 않게 연속변형을 할 수 있기 때문이다. 그림8을 참고하라. 즉 덴–닐슨–베어 정리는, 각각의 사상류가 곡면 위의 폐곡선들의 구성에 어떤 영향을 주는지에 대한 정보를 준다고 생각할 수 있는데 도려낸 구멍을 따라 만든 덴 꼬기는 곡면위의 폐곡선들에게 연속변형을 고려하면 아무런 영향을 주지 못하는 것이다.

3. 곡면의 대칭군과 그래프의 대칭군

곡면의 서로다른 두 대칭군 사이의 관계뿐 아니라, 덴–닐슨–베어 정리는 구멍 뚫린 곡면의 대칭군과 그래프의 대칭군 사이의 관계를 제공하기도 한다.

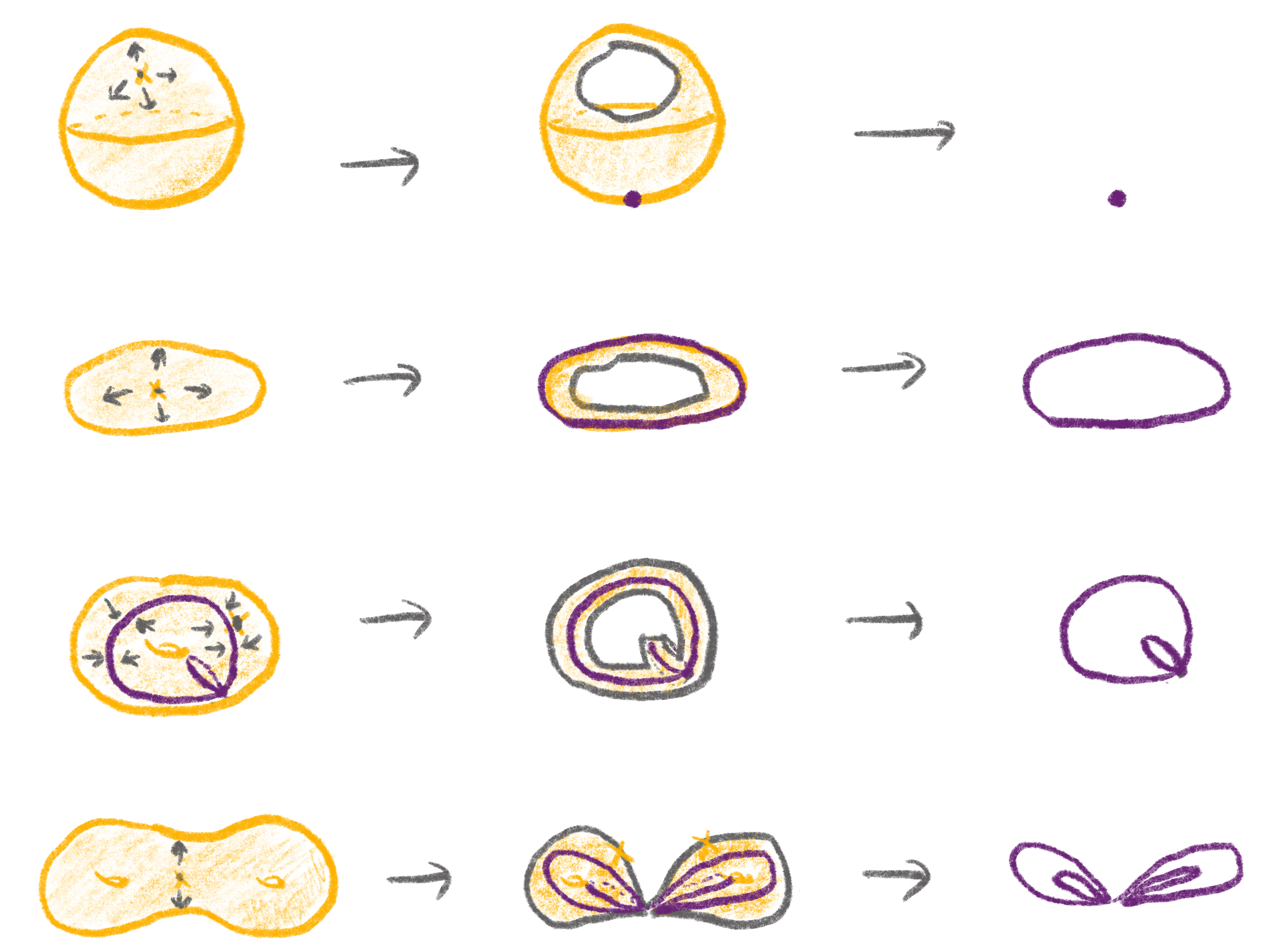
먼저, 곡면에 구멍이 있는 경우에는 기본군이 자유군 \(F_n\)이 된다. 이를 예시들을 통해 살펴보자. 그림 9에 시각적으로 표현되어 있다. 먼저, 기본군의 입장에서는 뚫음과 도려냄의 차이가 없음을 관찰하자.

A. 구멍이 하나 있는 구는 점으로 연속변형할 수 있다. 이는 폐곡선을 구멍 반대쪽으로 몰아 연속적으로 한 점으로 수축할 수 있기 때문이다.

2. 구멍이 하나 있는 원판은 원으로 연속변형할 수 있다. 구멍 주위를 도는 하나의 단순폐곡선이 해당 자유군을 생성한다.

3. 구멍이 하나 있는 토러스는 잎이 2개 있는 장미그래프}¹¹로 연속변형할 수 있다. 그림 9의 세 번째 줄을 참조하라.

4. 구멍이 하나 있는 2인용 튜브는 잎이 4개 있는 장미그래프와 연속변형동치이다. 그림 9의 네 번째 줄 처럼, 먼저 구멍이 하나씩 뚫린 토러스 2개를 이어붙인 곡면으로 먼저 연속변형하고 나면 3을 이용해서 각 곡면을 잎 2개짜리 장미그래프로 연속변형할 수 있기 때문이다.

일반적으로, 구멍이 뚫린 곡면들은 적절한 그래프들로 연속변형할 수 있다. 지난 글에서 서로 연속변형으로 같은 공간은 기본군이 같다고 했고 그래프의 기본군은 자유군이라고 했다. 따라서 구멍이 있는 곡면 \(S\)의 경우에는 덴–닐슨–베어 정리의 공역 \(Out(\pi_1(S))\)가 \(Out(F_n)\)이 된다. 즉 곡면들의 연속변형동치군은 (그래프의 대칭군인) 자유군의 외부대칭군과 일치하게 된다.

따라서, 덴–닐슨–베어 정리의 특수한 경우로서, “도려낸 구멍은 없되 뚫린 구멍만 있는 곡면 \(S\)의 사상류군은 항상 적당한 그래프의 대칭군의 부분군”으로 생각할 수 있음을 얻어낼 수 있다. 2차원 곡면의 대칭군이 1차원 그래프의 대칭군의 일부로 생각할 수 있다니 흥미롭지 않은가?¹² 

덴–닐슨–베어 정리는 철학적으로는 재미있으나 그 응용은 많지 않다. 이는 기하군론학자 니콜라이 이바노프^{Nikolai Ivanov}의 저서 [4] 에서도 언급되었다:

In principle, (Dehn–Nielsen–Baer theorem) gives a purely algebraic description of mapping class groups and allow one to reduce every question about them to a purely algebraic question. Surprisingly, this reduction turned out to be not very successful. 

그러나 드물게, 덴–닐슨–베어 정리를 활용하면 그래프의 대칭군인 \(Out(F_n)\)의 성질을 뚫린 구멍을 가진 곡면 \(S\)의 대칭군인 \(Map(S)\)으로 가져올 수 있다. 예를 들어, 사상류군이 잉여유한^{residually finite}을 보일 때 덴–닐슨–베어 사상 \(\Phi\)를 활용하면 \(Out(F_n)\)의 잉여유한성을 그대로 이용할 수 있다. 군의 잉여유한성이란 쉽게 말하면 각 원소를 유의미한 유한군의 원소로 보는 방법이 존재한다는 성질이다. 이 성질은 유한군에서의 계산을 이용할 수 있다는 점에서 기하군론에서 매우 유용한 성질이다.

그래도 그래프의 대칭군과 곡면의 대칭군 사이에 상징적인 가교 하나를 놓았다는 것 자체로도 의미가 있다고 생각한다. 실제로, 그래프의 이론과 곡면의 이론은 닮은 점이 많고 각자의 결과가 서로 영향을 주며 발전해 왔다. 이러한 유사성을 수학자들은 “그래프와 곡면 사이에 상징적 사전(그림10)이 존재한다”고 표현한다. 이 사전은 가히 미완성 상태이며, 필자는 이 사전의 특히 그래프 측면에서 빈칸을 채워나가는 것에 관심이 많다.

다음시간에는 그래프와 곡면이 “무한한 타입”인 경우를 보고자 한다. 즉, 그래프에 무한히 많은 변과 꼭짓점을 허용하고, 곡면은 무한히 많은 사람을 태울 수 있는 튜브에 무한 번의 구멍을 뚫고 도려내는 것을 허용하면 두 대칭군의 담론이 어떻게 펼쳐지는지 알아볼 것이다.