지난 연재에서는 차익거래가 무엇인지 살펴보고, 매우 단순한 금융시장 모형에서 차익거래가 존재할 수 없는 조건과 수학적으로 동치인 부등식을 증명하였습니다. 이 단순한 모형을 이항 모형이라 했는데, 이는 안전자산과 위험자산을 각각 한 개씩만 포함하며 위험자산이 다음 미래 시점에 두 가지 가격만을 가질 수 있다고 가정하는 모형입니다. 이항 모형에서 위 부등식은 차익거래 기회가 존재하지 않기 위해 시장 내 모든 자산의 가격들이 만족해야 하는 `적절한 상태’를 의미합니다. 이를 반대로 생각하면, 가격을 책정하기 어려운 어떤 자산이 있을 때 차익거래 불가 조건을 이용하여 이 자산의 가격이 가져야 하는 `적절한 상태’에 대한 정보를 유추해낼 수 있습니다. 이처럼 차익거래 불가 원리를 이용하여 특정 자산의 적절한 가격을 찾는 것을 합리적 가격 결정rational asset pricing이라 합니다.
이번 연재에서는 합리적 가격 결정 원리가 사용된 이론 중 실제 금융 업계에서 가장 많이 쓰이고 있는 옵션 가격 결정 이론option pricing theory에 대해 설명하려고 합니다.
옵션의 이해
금융시장에는 주식, 채권뿐만 아니라 농산물, 석유, 금, 원자재 등의 실물자산도 있습니다. 더구나 이러한 기초자산underlying asset의 가치 변동을 바탕으로 파생된 여러 가지 금융 상품들이 있는데, 이를 파생상품derivatives이라고 합니다. 옵션option은 파생상품의 한 종류로, 어떤 기초자산을 특정 만기 시점expiration date이 되면 미리 정해진 행사가격strike price 또는 exercise price에 사고팔 수 있는 권리right를 주고받는 계약입니다. 이때 기초자산은 주로 주식과 같은 위험자산이고, 기초자산의 미래 가치에 따라 옵션의 미래 가치도 달라지므로 옵션도 위험자산의 일종입니다.
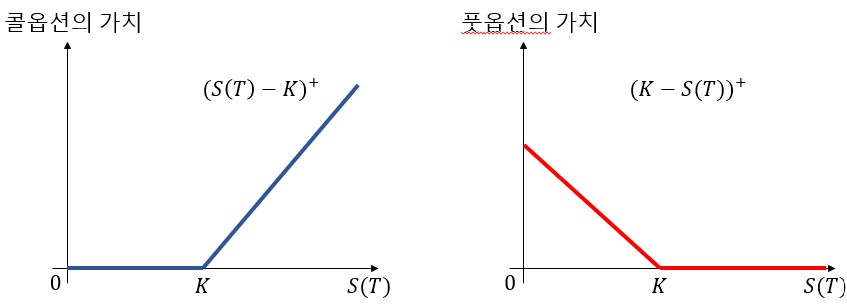
가장 널리 알려진 옵션으로 유럽형 콜옵션European call option과 유럽형 풋옵션European put option이 있는데, 유럽형 콜옵션은 기초자산을 만기 시점에 정해진 행사가격에 살 수 있는 권리를, 유럽형 풋옵션은 팔 수 있는 권리를 말합니다. 예를 들어, 지난 연재에서 설명한 이항 모형에서 위험자산 \(S\)를 기초자산으로 갖고, 만기 시점이 \(t=1\)이며 행사가격이 \(K\)인 유럽형 콜옵션을 생각해 봅시다. 이때 기초자산 \(S\)의 만기 시점에서의 가격 \(S(1)\)이 행사가격 \(K\)보다 크다면, 콜옵션의 소유자는 이 옵션이 갖는 권리를 `행사’함으로써 가격이 \(S(1)\)인 기초자산을 더 적은 액수인 \(K\)만 지불하고도 살 수 있습니다. 이렇게 \(K\)를 지불하고 산 기초자산을 곧바로 그것의 가격인 \(S(1)\)에 팔아버리게 되면 콜옵션의 소유자는 \(S(1)-K\)만큼의 금액을 벌 수 있으므로, 이 경우 콜옵션의 가치는 \(S(1)-K\)라 할 수 있습니다. 반면에 기초자산의 만기 시점에서의 가격 \(S(1)\)이 \(K\)보다 작거나 같다면, 콜옵션 소유자는 굳이 콜옵션을 `행사’함으로써 현재 가격보다 더 비싼 가격인 \(K\)를 주고 기초자산을 살 이유가 없습니다. 이 경우 콜옵션의 가치는 \(0\)이 됩니다. 즉, 콜옵션의 만기 시점(\(t=1\))에서의 가치payoff는 두 가지 값의 최댓값인 \(\max \big(S(1)-K, 0\big) = \big(S(1)-K\big)^+\)으로 나타낼 수 있습니다. 비슷한 논리로 풋옵션의 만기 시점에서의 가치는 \(\max \big(K-S(1), 0\big) = \big(K-S(1)\big)^+\)으로 나타낼 수 있습니다.
이처럼 옵션의 만기 시점에서의 가치는 그때의 기초자산 가격 \(S(1)\)과 행사가격 \(K\)의 함수로 나타낼 수 있고, 현재(\(t=0\)) 시점에서는 \(S(1)\)의 값을 예측할 수 없기 때문에(이항 모형의 경우 \(s_u\) 또는 \(s_d\) 중 하나일 것이라는 사실만 알기 때문에), 옵션도 미래 가격을 예측할 수 없는 위험자산입니다.
이같은 위험자산을 기초자산으로 갖는 유럽형 콜옵션이라 하더라도, 행사가격 \(K\)와 만기 시점 \(T\)가 달라지면 다른 계약이 되기 때문에, 이론상으로는 무한히 많은 종류의 콜옵션이 있을 수 있습니다. 실제 금융시장에서 거래되는 대부분의 옵션은 만기일이 보통 1개월 간격으로 구분되는데, 우리나라의 경우 매월 두 번째 목요일이, 미국의 경우 세 번째 금요일이 만기일이라고 합니다. 옵션의 행사가격도 다양한 값들을 가질 수 있는데, 콜옵션의 경우 행사가격이 낮을수록 옵션의 가치는 높아집니다. 왜냐하면 행사가격이 더 낮은 콜옵션을 소유하고 있다면 똑같은 기초자산을 만기 시점에 더 낮은 가격으로 살 수 있는 권리를 갖고 있는 것이기 때문입니다.
여기서 중요한 질문은 옵션의 현재 가치premium가 얼마인지, 즉 옵션을 현재 시점(\(t=0\))에서 얼마에 사고팔아야 적당한 가격일까? 하는 것입니다. 만기 시점에서의 옵션 가치는 위 그래프에서 보듯이 기초자산 가격에 대한 함수 형태로 나타나지만, 현재 시점에서의 옵션 가격을 구하는 것은 쉬운 문제가 아닙니다. 더구나 앞서 설명한 유럽형 콜/풋옵션 이외에도 미국형American, 아시아형Asian, 이색형Exotic 옵션 등 매우 다양하고 기괴하기까지 한 조건들이 포함되어 있는 수십 가지의 옵션 계약들이 존재합니다. 이러한 옵션의 현재 가격을 구하는 이론을 옵션 가격 결정 이론option pricing theory이라고 하며, 여기서 차익거래 불가 원칙no arbitrage principle이 중요한 역할을 합니다.
이항 모형에서의 옵션 가격 결정
지난 연재에서 설명한 이항 모형을 떠올려보고, 이 모형의 위험자산 \(S\)를 기초자산으로 갖는 (유럽형) 콜옵션 \(C\)를 생각해 봅시다. 다음 그림과 같이 만기 시점(\(t=1\))에서의 콜옵션의 가치 \(C(1)\)이 가질 수 있는 두 가지 값을 \(c_u = (s_u-K)^+\)와 \(c_d=(s_d-K)^+\)라고 합시다. 그리고 이 콜옵션과 항상 같은 미래 가치를 갖는 복제 포트폴리오replicating portfolio \(\pi = (\pi^B, \pi^S)\)라는 것을 만들어 내려고 합니다. 이 포트폴리오의 만기 시점에서의 가치는 \(V^{\pi}(1) = \pi^B \times B(1) + \pi^S \times S(1)\)와 같이 표현할 수 있고, 이는 아래 그림과 같이 \(\pi^B b_0(1+r) + \pi^S s_u\)와 \(\pi^B b_0(1+r) + \pi^S s_d\)의 두 가지 값을 가질 수 있습니다.
미래(\(t=1\))에 일어날 수 있는 두 가지 상황에서 복제 포트폴리오와 콜옵션의 가치가 항상 갖도록
다음과 같이 두 등식
\(\pi^B b_0(1+r) + \pi^S s_u = c_u\)
\(\pi^B b_0(1+r) + \pi^S s_d = c_d\)
을 세우고, 이를 \(\pi^B\)와 \(\pi^S\)를 미지수로 하는 연립방정식으로 생각하여 풀게 되면
\(\pi^B = \frac{c_d s_u-c_u s_d}{b_0(1+r)(s_u-s_d)}\), \(\qquad \pi^S = \frac{c_u-c_d}{s_u-s_d}\)
임을 알 수 있습니다. 이제 우리는 미래(\(t=1\)) 가치가 항상 똑같은 두 자산(복제 포트폴리오 \(\pi\)와 콜옵션 \(C\))이 있고, 차익거래 불가 원칙에 의하면 두 자산의 현재(\(t=0\)) 가치도 같아야 합니다 (만약 미래 가치가 항상 같은 두 자산의 현재 가치가 다르다면, 우리는 현재의 시세차익을 이용하여 차익거래를 만들어낼 수 있습니다). 복제 포트폴리오의 현재 가치는 위에서 구한 \(\pi^B\)와 \(\pi^S\)를 이용하면
\(V^{\pi}(0)\) = \(\pi^B \times b_0 + \pi^S \times s_0\) = \(\frac{c_d s_u-c_u s_d}{(1+r)(s_u-s_d)}\)+\(\frac{(c_u-c_d)s_0}{s_u-s_d}\)
\((0.1)\)
와 같음을 알 수 있으므로 콜옵션의 현재 가격 \(C(0)\)의 값도 이와 같아야 합니다. \(c_u\)와 \(c_d\)의 값이 기초자산 \(S\)의 두 미래 가격인 \(s_u\)와 \(s_d\), 그리고 행사가격 \(K\)의 함수로 나타난다는 것을 기억하면, 등식 \((0.1)\) 의 우변은 모두 현재 시점에 알고 있는 값들로 이루어져 있습니다.
이처럼 안전자산 \(B\), 기초자산 \(S\)로 이루어진 콜옵션의 복제 포트폴리오를 만들고 차익거래 불가 원칙을 통해 콜옵션의 현재 가격을 식 \((0.1)\) 과 같이 계산해 낼 수 있습니다. 풋옵션의 현재 가격도 위와 비슷한 원리로 계산할 수 있습니다.
위험중립 확률 측도
앞서 설명한 이항 모형에서 옵션 가격을 구하는 과정에는 중요한 원리가 숨어 있습니다. 등식\((0.1)\)에서 구한 콜옵션의 현재 가격을 \(c_u\), \(c_d\)가 포함된 항끼리 나누어 나타내면
\(C(0)\) = \(\frac{c_d s_u-c_u s_d}{(1+r)(s_u-s_d)}\)+\(\frac{(c_u-c_d)s_0}{s_u-s_d}\)
= \(\frac{1}{1+r}\bigg( \frac{(1+r)s_0-s_d}{s_u-s_d}c_u\) + \(frac{s_u-(1+r)s_0}{s_u-s_d}c_d \bigg)\)
와 같이 표현되는데, 이때
\(q = \frac{(1+r)s_0-s_d}{s_u-s_d}\)
\((0.2)\)
와 같이 정의하면
\(1-q = \frac{s_u-(1+r)s_0}{s_u-s_d}\)
임을 쉽게 계산할 수 있습니다. 그러므로 콜옵션의 초기 가격은 \(q\)와 \(1-q\)를 이용하면
\(C(0) = \frac{1}{1+r} \Big(q c_u + (1-q)c_d \Big)\)
\((0.3)\)
와 같이 표현됩니다. 그리고, 지난 연재에서 차익거래 불가 원칙과 동치라고 증명한 부등식 (0.1)에 의하면 \(0 < q < 1\)이 성립함을 알 수 있으므로, \(q\)를 콜옵션 가격이 만기 시점(\(t=1\))에서 \(c_u\)가 되는 새로운 확률이라고 생각할 수 있습니다.
즉, 위 그림과 같이 \((0.1)\)서 구한 옵션의 초기 가격 \(C(0)\)가 \(q\)의 확률로 \(c_u\)가 되고, \(1-q\)의 확률로 \(c_d\)가 되는 새로운 확률 측도probability measure \(Q\)를 생각할 수 있고, \(E^Q\)를 이 새로운 확률 측도에 대한 기댓값expectation이라 할 때, 등식 \((0.3)\)의 우변을
\(C(0) = \frac{1}{1+r} \Big(q c_u + (1-q)c_d \Big) = \frac{1}{1+r} E^Q[C(1)]\)
\((0.4)\)
와 같이 표현할 수 있습니다. 이때 등식 \((0.2)\)에서 정의된 \(q\)를 위험중립 확률risk-neutral probability, 새 확률 측도 \(Q\)를 위험중립 확률 측도risk-neutral probability measure라고 부릅니다. 이에 반해 지난 연재에서 이항 모형을 묘사할 때 등장했던 확률 \(p\)(기초자산 \(S\)의 가격이 \(s_u\)가 되는 확률)를 자연 확률physical probability이라고 부르며 이로 인해 사용되었던 확률 측도를 \(P\)라 표기하고 자연 확률 측도physical probability measure라고 부릅니다.
위험중립 확률 \(q\)가 갖는 의미를 자세히 설명하기 위해, 콜옵션의 가격을 안전자산의 가격으로 나눈 분수 \(\frac{C}{B}\)를 생각해 봅시다. 금융에서는 이와 같이 어떤 자산의 가격을 안전자산의 가격으로 나눈 것을 (안전자산의 가격에 대하여) 할인된 자산 가격discounted asset price이라 부릅니다. 등식
\((0.4)\)의 양변을 초기 안전자산 가격인 \(B(0)\)로 나누면
\(\frac{C(0)}{B(0)} = \frac{1}{B(0)(1+r)} E^Q[C(1)] = E^Q \left[\frac{C(1)}{B(1)}\right]\)
\((0.5)\)
와 같이 표현할 수 있고, 이 등식에서 \(B(0), B(1)\)를 좌변에 몰아놓고 양변에서 1씩 빼면,
\(\frac{B(1)}{B(0)}-1 = E^Q \left[\frac{C(1)}{C(0)} – 1\right]\)
\((0.6)\)
와 같은 등식을 얻습니다.
마지막 등식 \((0.6)\)이 시사하는 바를 설명하자면, 새롭게 정의된 위험중립 확률 측도 \(Q\)에 대하여 콜옵션의 수익률 \(\frac{C(1)-C(0)}{C(0)}\)의 기댓값은 안전자산의 수익률 \(\frac{B(1)-B(0)}{B(0)} = r\)과 같아야 한다는 것입니다. 즉, 위험중립 확률 \(q\)는 옵션의 기대수익률을 무위험이자율 \(r\)과 같아지도록 만드는 데 필요한 옵션 가격 상승 움직임의 확률입니다. 등식 \((0.5)\)로부터 알 수 있는 사실은, 위험중립 확률 \(q\)가 옵션의 할인된 자산 가격 \(C(1)/B(1)\)의 기댓값이 현재 할인된 자산 가격과 같아지게 만드는 상승 움직임의 확률임을 의미합니다.
만약 콜옵션의 초기 가격이 등식 \((0.1)\) 또는 \((0.3)\)에서 주어진 값과 달라 등식 \((0.6)\)이 성립하지 않는다면, 콜옵션의 기대수익률과 안전자산의 기대수익률 사이의 차이를 이용하여 차익거래를 만들어낼 수 있습니다. 다시 말해, 등식 \((0.1)\) 또는 \((0.3)\)에서 계산된 값은 이항 모형에서 차익거래가 없기 위한 콜옵션의 `적절한 가격’임을 의미합니다. 또한, 등식 \((0.1)\) 또는 \((0.3)\)을 살펴보면, 처음 이항 모형을 정의할 때 정한 위험자산의 가격 상승 확률, 즉 자연적 확률 \(p\)는 콜옵션의 초기 가격에 전혀 영향을 끼치지 않음을 알 수 있고, 오직 위험중립 확률 \(q\)로 인해 옵션 가격이 결정된다는 것을 알 수 있습니다.
마팅게일 확률 측도와 자산 가격 결정의 기본 정리
이제 앞에서 살펴본 이항 모형을 다음 그림과 같은 다단계 이항 모형multi-step binomial model으로 확장해 봅시다.
먼저 두 수 \(u\)와 \(d\)를 다음과 같이 정의하고
\(u = \frac{s_u}{s_0} \qquad d = \frac{s_d}{s_0}\)
시간을 나타내는 변수인 \(t\)가 \(0\) 또는 자연수 값을 가질 수 있다고 합시다. 시간 \(t=i\)일 때 위험자산의 가격이 \(S(i)\)라면 그 다음 시간 \(t=i+1\)에서의 가격은 \(p\)의 확률로 \(u \times S(i)\)가 되거나 \(1-p\)의 확률로 \(d \times S(i)\)가 됩니다. 그럼 파란색 부분 그림과 같이 \(S(0)\)가 `뿌리’가 되고 각 점node에서 가지branch가 두 갈래로 뻗어 나가지만 다시 만나기도 하는 이항 나무recombining binomial tree 구조의 그래프를 얻을 수 있습니다. 예를 들어 서로 다른 두 가지가 처음 만나는 점은 \(t=2\)일 때의 중간에 있는 점으로, 이때 \(S(2) = s_{ud}\)는 \(uds_0\)와 같은 값을 갖습니다.
이제 만기 시점이 \(t=T\)이고 행사가격이 \(K\)인 콜옵션이 있다면, 만기 시점에서 콜옵션의 가치는 \(C(T) = \big(S(T)-K\big)^+\)와 같습니다. 예를 들어 만기 시점이 \(T=2\)라고 가정하면, 주황색 부분 그림에서 \(C(2)\)의 중간값은 \(c_{ud} = (s_{ud}-K)^+\)와 같습니다. 이제 빨간색 부분으로 표시된 부분 나무subtree를 살펴보면, 그림 2의 콜옵션 나무 그래프와 유사한 형태로, 복제 포트폴리오를 만드는 방법을 통해 위험중립 확률 \(q\)를 구하고 \(C(1)=c_u\)인 점에서의 콜옵션의 가격을 구할 수 있습니다. 같은 방법을 \(c_d, c_{ud}, c_{dd}\)를 포함하는 부분 나무에도 반복하여 \(C(1)=c_d\)인 경우의 콜옵션 가격도 구할 수 있습니다. 이렇게 얻어진 \(c_u\), \(c_d\)에서의 콜옵션 가격을 마지막으로 \(C(0), c_u, c_d\)를 포함하는 부분 나무에도 같은 방법을 적용하면 최초 시점에서의 콜옵션 가격 \(C(0)\)를 구할 수 있습니다. 그리고 위에서 설명한 것과 같은 방법으로
\(E^Q \left[\frac{C(2)}{B(2)}\right] = \frac{C(0)}{B(0)}, \qquad E^Q \left[\frac{C(2)}{B(2)}\Bigg|\frac{C(1)}{B(1)}\right] = \frac{C(1)}{B(1)}\)
임을 증명할 수 있습니다. 이때 마지막 등식에서 어떤 두 확률변수 \(X, Y\)에 대해 \(E[X|Y]\)는 조건부 기댓값conditional expectation을 의미하는 것으로, 확률변수 \(Y\)의 값을 알고 있다는 가정 하에 계산된 확률 변수 \(X\)의 기댓값을 의미합니다. 이제 이 두 등식을 만기 시점이 임의의 자연수 \(t=T\)인 일반적인 경우로 확장하면
\(E^Q \left[\frac{C(T)}{B(T)}\right] = \frac{C(0)}{B(0)}, \qquad E^Q \left[\frac{C(i+1)}{B(i+1)}\Bigg|\frac{C(i)}{B(i)}\right] = \frac{C(i)}{B(i)}, \quad i = 0, 1, \cdots, T-1\)
\((0.7)\)
와 같은 식들이 성립함을 보일 수 있는데, 이는 할인된 콜옵션 가격 \(\frac{C}{B}\)가 위험중립 확률 측도 \(Q\)에 대하여 마팅게일martingale이라는 것을 의미합니다.
어떤 이산 확률 과정discrete stochastic process \(M = \big(M(0), M(1), M(2), \cdots \big)\)이 있을 때, 주어진 확률 측도 \(P\)에 대하여 등식
\(E^P[M(n+1) | M(n)] = M(n)\)
이모든 \(n = 1, 2, \cdots\)에 대하여 성립한다면, \(M\)을 \(P\)-마팅게일이라 부릅니다. 만약 \(M\)이 \(P\)-마팅게일이라면, 현재 \((t=n)\) 시점까지 주어진 \(M\)의 정보들을 토대로 다음 미래 \((t=n+1)\) 시점에서의 \(M\)의 확률 측도 \(P\)에 대한 기댓값은 현재 \(M\)의 값인 \(M_n\)이어야 한다는 것을 의미합니다. 마팅게일의 중요한 성질 중 하나는 기댓값이 일정하다는 것 \((E^P[M(n)] = E^P[M(n-1)] =\cdots=E^P[M(1)] = E^P[M(0)])\)입니다.
할인된 콜옵션 가격 \(\frac{C}{B}\)가 \(Q\)-마팅게일이라는 사실 \((0.7)\)로부터, 옵션 가격을 결정할 때 쓰였던 위험중립 확률 측도 \(Q\)를 마팅게일 확률 측도martingale probability measure라고도 부릅니다. 등식\((0.7)\)을
\(E^Q \left[\frac{C(T)}{C(0)}-1\right] = \frac{B(T)}{B(0)}-1, \qquad E^Q \left[\frac{C(i+1)}{C(i)}-1\Bigg|\frac{C(i)}{B(i)}\right] = \frac{B(i+1)}{B(i)}-1, \quad i = 0, 1, \cdots, T-1\)
와 같이 다시 표혐하면, 현재 \((t=0)\) 에서 만기 시점 \((t=T)\) 까지의 콜옵션의 (위험중립 확률 측도 \(Q\)에 대한) 기대 수익률은 안전자산의 동기간 수익률과 같아야 하며, 각 세부 기간 (\(t=i\)에서\(t=i+1\)까지) 의 콜옵션 기대 수익률도 동기간 안전자산의 수익률과 같아야 한다는 것을 의미합니다. 만약 콜옵션의 수익률의 기댓값이 안전자산의 수익률과 다르다면, 이 기댓값의 차이를 이용하여 차익거래를 만들어낼 수 있음을 보일 수 있습니다. 이를 통해 다음의 정리를 나타낼 수 있는데, 이는 금융수학에서 가장 핵심이 되는 정리입니다.
자산 가격 결정의 기본 정리Fundamental theorem of asset pricing:
금융시장에서 차익거래가 불가하다는 조건과 마팅게일 확률 측도가 존재한다는 조건은
서로 동치이다.
다시 말해, 차익거래가 불가하다는 가정을 통해 주어진 시장 모형의 마팅게일 확률 측도 \(Q\)의 존재성을 알 수 있고, 이 측도를 통해 임의의 위험자산 \(R\)의 할인된 자산가격 \(\frac{R}{B}\)이 항상 \(Q\)-마팅게일이 된다는 성질을 이용할 수 있습니다.
연속 시간 모형과 블랙-숄즈 공식
이제까지 자산 가격 결정의 기본 정리를 보다 알기 쉽게 설명하기 위해 이산 시간 모형discrete time model의 일종인 이항 모형을 사용하였습니다. 그러나 시간이 연속적으로 흐르는 것을 가정하는 연속 시간 모형continuous time model에서도 자산 가격 결정의 기본 정리가 성립하고, 마팅게일 확률 측도를 이용해 유럽형 옵션의 가격을 찾을 수 있습니다.
주어진 미래 시점 \(T\)에 대해, 시간 간격 \([0, T]\)를 똑같이 \(N\)개의 하위 간격subinterval으로 나누고, \(T/N\) 단위 시간이 지날 때마다 위험자산 \(S\)의 가격이 두 가지로 바뀔 수 있는 \(N\)-단계 이항 모형을 생각할 수 있습니다. 이렇게 얻게 되는 \(N\)-단계 이항 나무 구조를 적당히 크기변환scaling한 후 \(N\)을 무한히 크게 만들면, \(t \in [0, T]\) 시점에서의 위험자산의 가격 \(S(t)\)가 다음과 같은 확률 미분 방정식
\(dS(t) = \mu S(t) dt + \sigma S(t) dW(t), \qquad S(0) = s_0\)
\((0.8)\)
을 만족한다는 것을 보일 수 있습니다. 이러한 식을 만족하는 확률 과정 \(S\)를 기하 브라운 운동geometric Brownian motion이라 하는데, 여기서 \(\mu\)는 표류 계수drift, \(\sigma\)는 변동성volatility이라 불리는 상수들이고, \(W(t)\)는 브라운 운동Brownian motion입니다.
이처럼 가격이 기하 브라운 운동으로 주어진 위험자산을 기초자산으로 갖는 유럽형 콜/풋옵션의 초기 가격 \(C(0), P(0)\)은 차익거래 불가 조건을 통한 마팅게일 확률 측도를 이용하여 다음과 같이 구할 수 있는데
\(C(0) = \Phi(d_+) s_0 – \Phi(d_-)Ke^{-T}\), \(\qquad P(0) = \Phi(-d_-)Ke^{-T} – \Phi(-d_+)s_0\),
\(\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-\frac{z^2}{2}}dz\), \(d_{+} = \frac{1}{\sigma \sqrt{T}} \Big[ \ln \frac{s_0}{K} + \big( r+\frac{\sigma^2}{2} \big) T \Big]\), \(d_- = d_+ – \sigma\sqrt{T}\)
이것이 1970년대 초반에 발표된 블랙-숄즈 또는 블랙-숄즈-머튼 공식Black-Scholes-Merton formula입니다. 이 공식이 처음 알려진 후 옵션을 다루는 금융 산업 전반에서 현재까지도 활발히 쓰이고 있으며, 이 공식을 발견한 숄즈와 머튼은 1997년 노벨 경제학상을 수상하였습니다 (블랙은 1995년 사망하여 안타깝게 수상하지 못했습니다).
마치며
실제 금융시장에서 거래되는 유럽형 옵션들의 가격은 실시간 수요/공급에 따라 결정됩니다. 또한, 옵션의 기초자산(특정 주식)의 가격이 확률 미분 방정식\((0.8)\) 을 정확히 따른다고 볼 수도 없는데, 실제 시장에서 주식의 변동성 \(\sigma\)는 상수가 아니고 계속 변화하며, 옵션 가격에 영향을 미치는 무위험이자율 \(r\)도 시간이 지남에 따라 바뀔 수 있습니다. 그러나 위와 같이 기하 브라운 운동을 가정하여 유도된 블랙-숄즈 공식은 유럽형 옵션의 가격을 가장 간단하면서도 잘 작동하는robust 이론으로 설명하기 때문에, 옵션을 다루는 대부분의 금융업 종사자는 블랙-숄즈 공식을 통해 해당 옵션의 `이론적 가격’을 추정하고 있습니다. 따라서 실제 옵션의 가격이 이론적 가격과 차이가 나는 상황이 발생한다면 전 세계 차익거래자arbitrageur들의 먹잇감이 되어 순식간에 이론적 가격으로 수렴하게 됩니다.
다른 종류의 옵션(미국형, 아시아형, 이국형 등)과 다양한 형태의 파생상품들의 가격도 차익거래가 불가하다는 가정과 할인된 자산 가격이 (마팅게일 확률 측도에 대해) 마팅게일이어야 한다는 조건을 이용하면 `이론적 가격’을 계산해 낼 수 있습니다. 하지만 유럽형 옵션의 블랙-숄즈 공식처럼 명시적인explicit 공식은 얻을 수 없고, 마팅게일 조건을 통해 유도된 어떤 편미분 방정식이나 확률 미분 방정식의 해를 수치 해석적인 방법으로 근사하여 파생상품의 가격을 계산해 냅니다.
이처럼 다양한 금융 상품의 적당한 이론적 가격을 찾는 연구는 블랙-숄즈 공식이 발표된 지 50여 년이 지난 현재까지도 계속되고 있으며, 차익거래의 수학적 정의를 조금씩 바꾸었을 때 얻게 되는 새로운 차익거래 불가 원칙들이 금융시장에 어떤 변화를 불러오는지에 대한 연구들도 활발히 진행되고 있습니다.