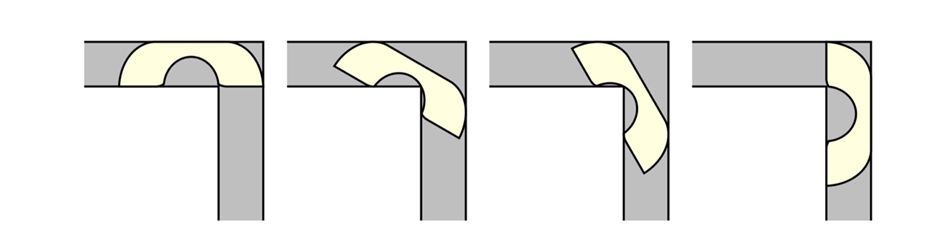
“직각 복도를 통과할 수 있는 가장 큰 소파는 무엇인가?”
이 단순한 질문은 수학계에서 반세기 넘게 풀리지 않은 퍼즐로 남아 있었다. 1966년, 캐나다 수학자 레오 모저가 처음 제안한 ’소파 옮기기 문제’는, 폭이 1인 \(L\)자 형태의 직각 복도를 통과할 수 있는 최대 면적의 평면 도형, 즉 ‘이상적인 소파’의 형태를 찾는 것이었다. 쉽게 말하면, 수평 복도에서 시작해 직각 코너를 돌아 수직 복도로 빠져나올 수 있는 도형 중 가장 넓은 것을 찾는 문제다. 이 문제는 초등학생도 이해할 수 있을 정도로 쉬움에도 불구하고 60년 가까이 명확한 해답이 나오지 않아 수학계의 도전 과제로 남아 있었다. 1992년, 수학자 조셉 거버Joseph Gerver는 복잡한 곡선으로 이루어진 도형을 통해 이 문제의 유력한 후보 해를 제시했지만, 그것이 정말 최적해optimal solution인지 증명되지 않은 채 수십 년이 흘렀다.
이러한 난제를 해결한 인물이 바로 백진언 박사다. POSTECH 수학과를 졸업하고, 미국 미시간대에서 박사 학위를 취득한 백 박사는 2024년 12월, 조셉 거버 교수가 제시한 소파 도형이 이 문제의 최적해임을 수학적으로 증명한 논문을 arXiv에 공개해 학계의 주목을 받았다. 백 박사의 논문은 아직 리뷰가 되기 전이지만, 그의 풀이가 옳다는 것이 학계의 전반적인 분위기다.
신촌의 한 카페에서 백진언 박사를 만나 소파 문제 증명에 대한 자세한 이야기를 들을 수 있었다. 그의 증명은 크게 두 단계로 줄일 수 있다. 그의 증명의 첫 번째 단계는 고려해야 하는 소파의 조건을 한정하는 것이다. 대략적으로 말하자면 최대 넓이의 소파의 형태가 거버 소파와 비슷하다는 것을 증명하는 단계이다. 그렇게 추려진 소파의 조건은 네 가지다.
(1) Monotone 소파일 것
(2) Balanced 소파일 것
(3) 움직이는 과정에서 90도만큼 회전할 것
(4) Injectivity condition을 만족할 것
여기서 (1)과 (2)는 거버 소파를 제시한 거버 교수가, 그리고 (3)에서 각도가 60도와 90도 사이에 있다는 것을 거버 교수가, 그 각도가 정확히 90도라는 것을 백진언 박사가 증명했다. (4)는 이 증명의 가장 핵심적인 부분인데, 백진언 박사가 스스로 떠올리고 증명해냈다. 각각의 조건을 조금 더 자세히 들여다보자.
(1) Monotone 소파일 것
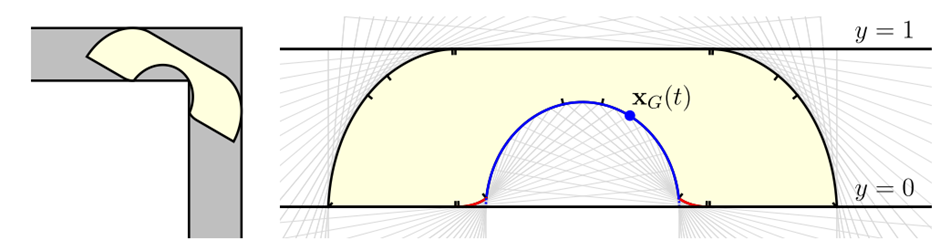
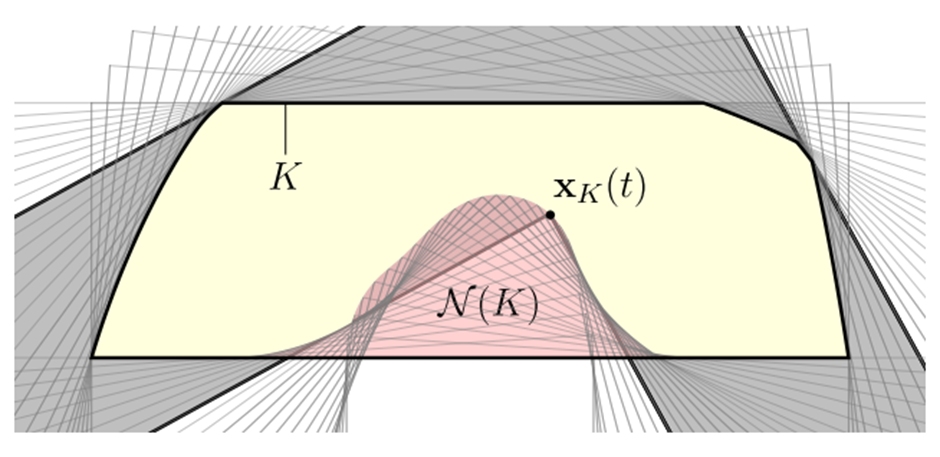
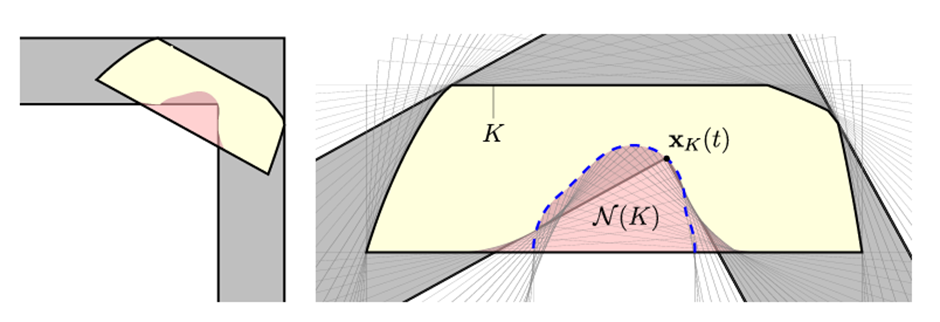
어떤 소파가 Monotone 소파라는 것은, 소파가 복도를 지나는 도중에 시계방향으로만 단조롭게 회전한다는 것이다. 즉 소파를 옮기는 와중에, 마치 차를 주차하듯 앞으로 갔다 뒤로 갔다 하지 않는다는 것이다. 또한 이 과정에서 이 소파는 복도의 바깥쪽 벽과 늘 접촉해 있다. 이 조건을 통해 우리는 소파를 복도의 교집합으로 볼 수 있으며, 복도의 바깥쪽 벽들이 접선이 되는 볼록한 도형 \(K\)를 정의할 수 있다. 그리고 이러한 볼록도형 \(K\)가 복도 안을 회전하면서, 복도의 안쪽 벽들이 깎는 부분을 \(\mathcal{N}(K)\)로 정의한다. 이렇게 정의하면 소파 S가 볼록도형 \(K\)에서 영역 \(\mathcal{N}(K)\)를 뺀 모양이 된다. 이러한 소파를 Monotone 소파라고 한다.
(2) Balanced 소파일 것
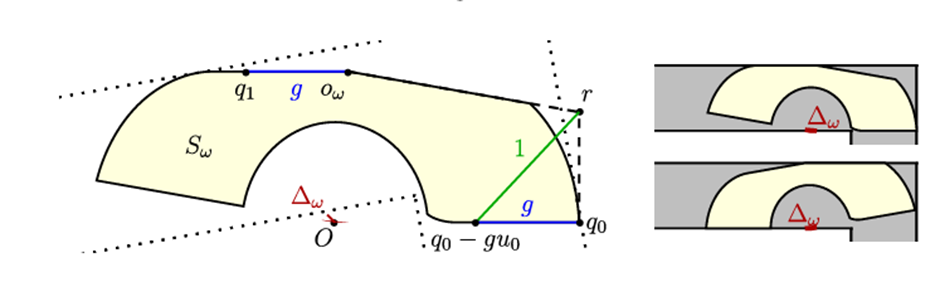
유한한 각도 집합 \(\Theta\)를 잡고, 소파 S를 \(\Theta\)의 각 각도만큼 돌아간 복도들의 교집합 \(S_{\Theta}\)로 근사하여 보자. 이때 \(S_{\Theta}\)는 다각형이 된다. 이때 Balanced 소파라는 것은 임의의 단위 벡터 \(\mathbf{v}\)에 대해 \(\mathbf{v}\) 방향의 법선 벡터를 가지는 변들의 총 길이가 \(-\mathbf{v}\) 방향의 변들의 총 길이와 같아지는 조건을 만족하는 소파를 말한다. 만약 이 조건을 만족하지 않는다면 복도의 일부를 변의 총 길이가 더 큰 방향으로 밀어 면적을 더 키울 수 있기 때문에, 최대 넓이를 가지는 소파일 수 없다. 이 조건은 다각형 소파들에 대해 먼저 정의되지만, 이러한 Balanced 조건을 만족하는 다각형 소파의 수열은 결국 최대 넓이의 소파로 수렴한다는 것이 증명된다. 이 조건은 이후 (3)의 90도 회전 조건과 (4)의 Injectivity condition을 이야기하는 데 큰 역할을 한다.
(3) 움직이는 과정에서 90도만큼 회전할 것
복도 \(L\)이 직각으로 꺾여 있다고 하더라도, 소파가 꼭 90°만큼 회전해야 한다는 법은 없다. 실제로 거버 교수는 1992년 최대 넓이 소파의 회전 각도 \(\omega\)가 60° 이상 90° 이하임을 보였다. 이후 Kallus와 Romik은 2017년 그 하한을 약 81.2°까지 끌어올렸다. 그리고 백진언 박사가 이 회전 각도가 정확히 90°라는 것을 증명해냈다. 증명 과정을 간단히 요약하자면 다음과 같다.
만약 어떤 최대 넓이의 소파 \(S\)가 \(\omega < 90^\circ\)만큼만 회전한다고 가정하면, 수평 방향의 균형 조건을 이용해 \(S\)가 실제로 \(90^\circ – \omega\)만큼 추가 회전할 수 있는 여유 공간이 있다는 것을 보일 수 있다. 따라서 최대 넓이의 소파는 복도를 통과하는 과정에서 \(90^\circ\)만큼 회전할 수 있다는 결론이 도출된다.
(4) Injectivity condition을 만족한 것
Injectivity condition이란 회전하는 복도의 안쪽 꼭짓점 궤적 \(\mathbf{x}(t)\)이 자기 자신과 교차하지 않는다는 것, 즉 injective한 함수라는 의미이다. 이 조건이 만족되면, 꼭짓점이 깎아낸 영역의 넓이를 그린의 정리Green’s theorem를 이용해 면적 공식으로 정확히 나타낼 수 있으며, 이는 증명에서 면적의 상한을 정밀하게 분석하는 데 중요한 역할을 한다.
\(|\mathcal{N}(K)| \geq \text{(blue region)} = \frac{1}{2} \int_0^{\pi/2} \mathbf{x}(t) \times \mathbf{x}'(t) \, dt\)
백 박사는 이 조건을 시뮬레이션을 통해 먼저 관찰했다. (2)의 Balanced 조건을 만족하도록 소파를 변화시키는 과정을 반복하다 보면, 모든 궤적이 스스로 교차하지 않고 injective하게 되는 현상을 볼 수 있었다고 한다. 이후 이 현상이 단순한 관찰에 그치는 것이 아니라 수학적으로 증명 가능하다는 것을 보이기 위해, balanced 조건에서부터 ODE를 유도해냈다.
\(\langle \mathbf{A}'(t), \mathbf{v}_t \rangle = \langle -\mathbf{B}'(t), \mathbf{v}_t \rangle + \langle \mathbf{x}'(t), \mathbf{v}_t \rangle\)
이때 회전 중 소파가 복도의 세 점 \(A(t)\), \(B(t)\), \(\mathbf{x}(t)\)에서 접한다고 가정하면 균형 조건이 하나의 등식으로 표현되지만, 실제로는 이러한 접점이 항상 존재한다고 보장할 수 없기 때문에, 접촉 여부와 무관하게 항상 성립하는 부등식 형태로 일반화하였다.
\(\langle A'(t), \mathbf{v}_t \rangle \leq \max\left( \langle -B'(t), \mathbf{v}_t \rangle, 0 \right) + \left| \langle \mathbf{x}'(t), \mathbf{v}_t \rangle \right|\)
이를 바탕으로 \(\langle \mathbf{x}'(t), \mathbf{u}_0 \rangle < 0\)를 보일 수 있고, 여기서 \(\mathbf{x}(t)\)가 자기 자신과 교차하지 않는다는 결론, 즉 Injectivity condition을 수학적으로 정당화할 수 있게 된다.
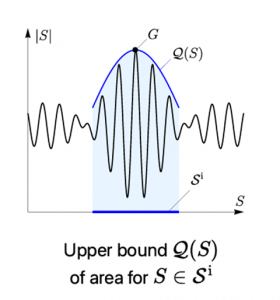
증명의 두 번째 단계는, 첫 번째 단계에서 추려낸 소파들 \(\mathcal{S}^i\) 위에서 넓이의 상한을 설정하는 것이다.
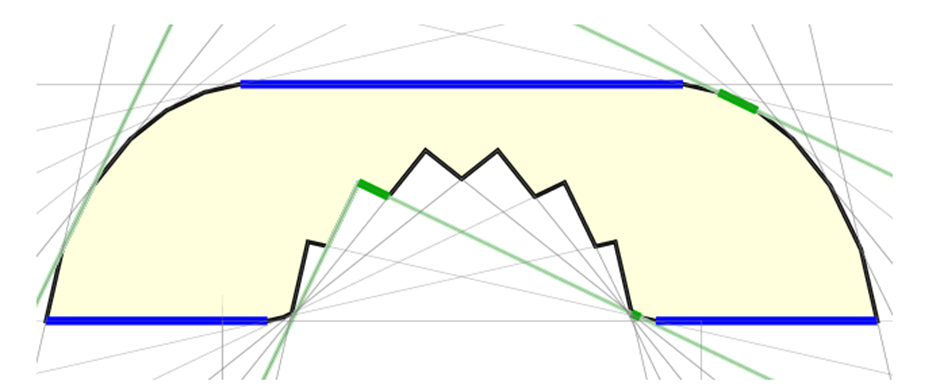
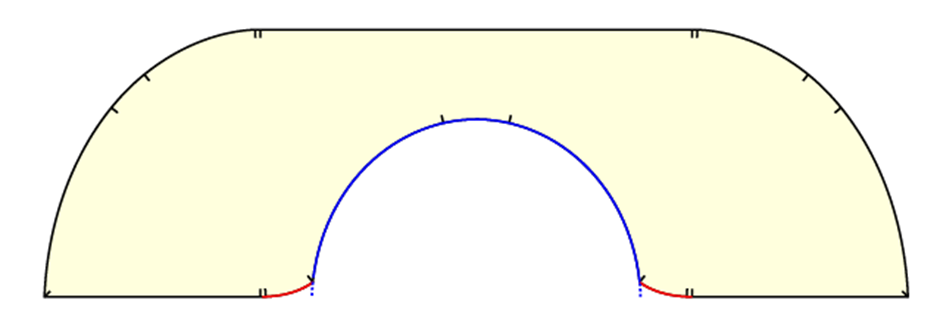
이를 위해 백 박사는 소파 \(S\)를 포함하는 더 큰 도형 \(R\)을 정의하고, 그 넓이 \(\mathcal{Q}(S)\)를 상한 함수로 삼는다. 이 도형 \(R\)은 하나의 중심(core, 그림의 파란선)과 두 개의 꼬리(tails, 그림의 빨간선)로 구성되며, Gerver 소파의 구조를 일반화한 형태다. 이후 도형 \(R\)의 핵심인 모자 부분cap \(K\)를 왼쪽, 가운데, 오른쪽 영역으로 나누고, 각각의 영역에서 벽 또는 꼭짓점이 깎아내는 기여만을 반영하여 면적을 계산한다. 특히 가운데 부분에서는 Injectivity condition을 통해 자기 교차가 없음을 활용하고, 그린의 정리를 통해 넓이 공식을 엄밀히 표현할 수 있다.
다음 단계에서는 이 함수 \(\mathcal{Q}(K)\)가 볼록 집합 위에서 정의된 이차식이고 오목함을 증명한다. 특히 Gerver의 소파 G에 대해서는 이 상한이 정확히 넓이와 일치함을 보여주고, G가 \(\mathcal{Q}\)의 국소 극대local maximum임을 증명함으로써, \(\mathcal{Q}\)가 이차식이라는 점을 이용해 넓이가 최대가 된다는 결론에 도달하게 된다.
백진언 박사는 이 문제를 풀겠다고 결심한 지 7년 만에 마침내 해결해냈다. 문제의 해결 방식에 대한 직관은 시작한 지 3년쯤 되었을 때 떠올랐지만, 이를 수학적으로 엄밀하게 증명하고 논문으로 정리하는 데에는 상당한 시간이 걸렸다. 처음에는 컴퓨터를 이용한 증명 방식으로 접근했고, 실제로 작동하는 증명 코드도 있었다. 하지만 그 코드는 너무 길고 복잡해서, 증명이 가능하다는 것은 확인할 수 있었지만 이를 완전한 증명으로 정리하는 데 어려움이 있었다고 한다. 결국 그는 증명을 단순화하려고 노력했고, 그 과정에서 컴퓨터가 필요 없어졌다. 2년 동안 공들였던 코드가 필요 없어진 것에 대해 백 박사는 “시원섭섭했다. 그렇지만 이거를 쓰려면 증명을 발표하는데 1년은 더 걸렸을 거 같더라. 지금 끝내는 것이 1년 뒤에 끝내는 것보다 훨씬 낫다고 생각했다. 복잡미묘한 마음이었다.”라고 표현했다.
백진언 박사가 길고 긴 7년이라는 시간동안 한 문제를 잡고 풀어낼 수 있었던 힘은 어디서 왔을까? 백 박사는 어린 시절 XMO라는 올림피아드 카페에 올라와 있는, 다른 사람들이 못 푸는 문제를 푸는 것을 즐겼다. 몇 달 동안 같은 문제를 고민하여 풀어내던 경험이 소파 문제를 해결하는 데도 큰 도움이 됐다고 한다. “그러면서 길게 보았을 때 풀릴 가능성이 얼마나 있는지, 그 감각이 생겼던 거 같다. 소파는 시작할 때부터 왠지 될 거 같은 느낌이 있었다.”라고 말했다.
백진언 박사는 어린 시절 힘든 가정 환경 속에서 자랐다. 수학을 잘 하면 돈을 더 빠르고 많이 벌 수 있는 길이 있었을 텐데, 굳이 고된 순수 수학의 길을 갈 수 있었던 원동력이 무엇인지 물어봤다. “초등학교 3,4학년 때 수학을 직업으로 할 수 있다는 걸 알게 된 이후로 계속 꿈이 수학자였던 것 같다. 그 관성으로 여기까지 왔다.”면서, “다른 직업을 하더라도 수학이라는 아름다움은 놓지 못했을 거 같다.”고 했다. 또한 “가정환경은 안 좋았지만, 어머님께서 정보를 열심히 찾아 주셨다. 그렇게 KAIST 사이버 영재교육원을 알게 되었다.”라고 했다. 이때 본인을 가르쳐주었던 KAIST 대학생이 현재 백 박사의 박사후연구원 지도교수인 이준경 교수다. “영재학교를 준비하는 과정에서 중학교 선생님들도 사비를 모아 노트북을 사주시고, 영어학원을 보내주시는 등 물심양면으로 도와주셨다. 그렇게 영재학교를 간 이후에는 영재학교 선생님들의 도움을 많이 받았다. 이러한 배려들 때문에 지금 여기까지 올 수 있었다. 그래서 언젠가 이걸 돌려줘야겠다는 생각을 계속 가지고 있다.”라는 이야기를 전해주었다. 백 박사는, 힘든 환경 속에서도 주위의 따뜻한 손길과 제도의 도움을 통해 성장해온 우리 사회가 함께 길러낸 인재라 할 수 있다.
백진언 박사는 이후에도 소파 문제와 같은 ‘기하 최적화’ 문제에 도전해보고자 한다. 지금 관심있는 문제는 다각형을 어떻게 하면 최대한 밀도 높게 패킹할 수 있는지에 관한 문제다. 또한 4차원 구 패킹 문제도 컴퓨터를 이용해서 풀고 싶다는 포부를 가지고 있다.
