6월의 퍼즐에 참여해주신 모든 분들께 감사드리며,
참여해주신 분들 중 정답과 함께 좋은 풀이를 보내주신
신동건 님에게 문화상품권을 전달하겠습니다.
문제 1.
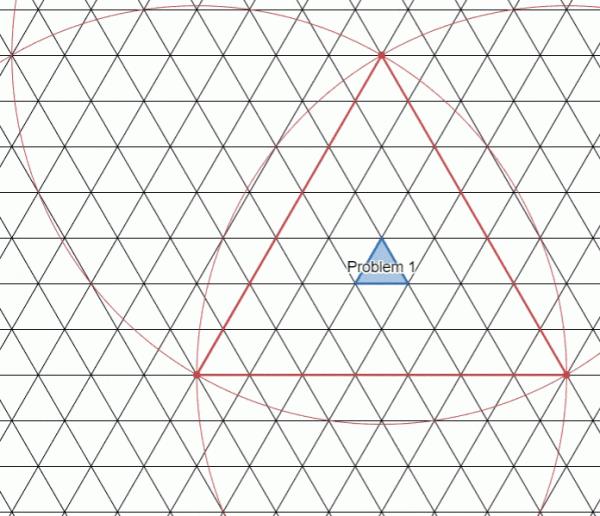
위와 같이 60도 각도로 한 점에서 만나는 세 직선이 있으면 정삼각형의 꼭짓점을 세 직선 위에 하나씩 둔 채로 360도 회전을 할 수 있다. 이 같은 움직임이 가능하단 증명은 삼각형의 외접원을 그린 후 원주각을 고려하면 쉽게 할 수 있다.
문제 1의 해답은 위의 애니메이션에서 첫 1/6에 해당하는 움직임만 수행하면 된다.
문제 2.
여기서는 파란색 삼각형 때문에 위의 방법이 통하지 않는다. 하지만,

움직임을 수행하다 보면, 도중에 위와 같이 세 점이 정확히 격자점 위에 놓이는 순간이 오게 된다. 주황색 점들 사이의 거리가 정확히 7이라는 것은 코사인법칙을 이용해 계산할 수 있다. 이 상황에서 삼각형을 왼쪽으로 3만큼 평행이동한 다음 나머지 움직임을 수행하면

이렇게 원하던 대로 삼각형이 뒤집어진다.
다음은 정답자로 선정된 신동건님의 풀이입니다.
첫 번째 문제를 풀기 위해서는 격자 위에서 정삼각형을 돌릴 방법을 찾아야 한다. 당연하게도 그 자리에서 돌리면 격자를 벗어나게 되므로 움직이면서 돌려야 한다. 문제는 어떻게 움직여야 하느냐지만 여기에 유용한 사실이 하나 있다. 바로 작은 원이 큰 원의 내부를 구를 때 작은 원의 점이 그리는 궤적인 하이포사이클로이드hypocycloid는 큰 원의 지름이 작은 원의 두 배일 경우 완벽한 직선을 그린다는 것이다. 그 말인 즉, 정삼각형에 외접하는 원과 정삼각형의 꼭짓점을 중심으로 하고 길이가 7√3/2인 원을 기준으로 작은 원을 굴리면 된다.
두 번째 문제는 여기서 삼각형을 돌리는 중간에 이동할 수 있는지를 알아야 한다. 각각의 꼭짓점은 각각 평행하지 않는 격자 선을 따라 이동하고 있으니 만약 다른 방향으로 삼각형을 이동하고자 하면 모든 꼭짓점이 격자점 위에 있어야 한다. 운이 좋게도 (아마도 그렇게 정해졌겠지만) 길이가 각각 3,5,7인 삼각형은 가장 큰 각이 120º이고 이는 3²+5²-2×3×5×cos120º=7²을 통해 확인할 수 있다. 돌리는 중간에 평행하게 이동시키고 마저 돌리면 파란 정삼각형이 벗어나지 않게 돌릴 수 있다. 여담으로 그림에서 항상 정삼각형임을 나타내기 위해 원을 그려두었다.
GIF가 작동하지 않을 경우 https://www.desmos.com/calculator/gjvpwccixh 에서 확인할 수 있다.



